OOF2: The Manual
In OOF2, before creating a finite element mesh, you must first
create a Skeleton. The Skeleton defines only the
geometry of the mesh. It does not include
any information about Equations, Fields or finite element
shape functions. All of that information is in the Mesh
class, which will be discussed later.
The Skeleton is an intermediate step between the pixelized Microstructure
and the finite element solution. It represents the finite
element discretization of the Microstructure. One Microstructure may contain
many Skeletons, representing different discretizations. One
Skeleton, in turn, may generate many Meshes, allowing different
physics or different solution methods to be tried in a single
geometry.
The Skeleton Task
Page contains tools for creating and modifying Skeletons.
The Skeleton
Info toolbox contains tools for examining the details of
a Skeleton in the graphics window.
When a Skeleton is constructed, it can be declared to be
periodic in the x or y directions, or neither, or both. If it
is periodic, then any modifications performed on one edge will
also apply to the opposite edge, Every Node or Segment on a
periodic edge will have a matching partner on the opposite
edge. All skeleton modifications will maintain the
periodicity of the skeleton.
Periodic
boundary
conditions can only be applied to Meshes derived from
periodic Skeletons. However, non-periodic boundary conditions
can be applied to either periodic or non-periodic Skeletons.
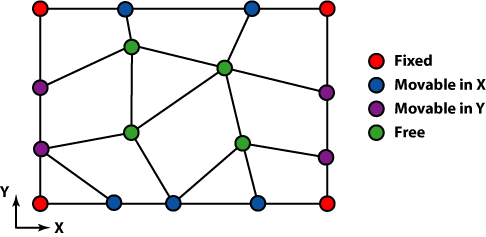
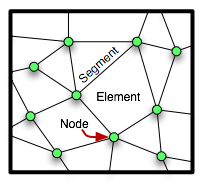
Skeletons are composed of triangular and quadrilateral
elements, as shown in Figure 2.3. These are non-overlapping
polygons that completely cover the Microstructure. Skeleton elements
will be converted directly into Mesh
Elements when a Mesh is created.
Many Skeleton operations operate on the set of currently
selected elements. Elements may be selected by the Skeleton
Selection Task Page and the Skeleton
Selection toolbox.
Skeleton elements inherit their Material Properties from
the pixels beneath them in the Microstructure.
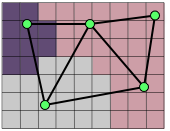
If the Skeleton geometry is to be a good approximation of the
Microstructure geometry, then all of the pixels lying beneath an
element should have the same assigned Material. The
homogeneity of a Skeleton element is a
measure of how well the element achieves this goal. (See
Figure 2.4.)
The homogeneity is computed by finding the area of the
element that overlies each category of
pixel. Pixels
that have different assigned Materials or belong to
different “meshable”
PixelGroups are in different categories. The
category claiming the largest area of the element is the
dominant category. The homogeneity is
defined as the ratio of the area of the dominant category to
the area of the element as a whole. A completely
homogeneous element has a homogeneity of 1.0. An element
made up of N equal components has a homogeneity of 1/N. The
Material assigned to an element is the Material of its
dominant pixel category.
![[Note]](IMAGES/note.png) |
Note |
|---|---|
|
The color of the pixels in an |
Figure 2.4. Skeleton Element Homogeneity
Many of the tools for modifying Skeletons, such as Anneal
and Smooth,
work by reducing an effective energy
functional,
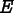 ,
of the mesh. This functional assigns
a number between 0 and 1 to each element. It is called an
energy because of its role in the
,
of the mesh. This functional assigns
a number between 0 and 1 to each element. It is called an
energy because of its role in the Annealing
operation, where it plays the role of the energy in a
statistical mechanical simulated annealing process.
The energy functional has two contributions, a homogeneity
energy,
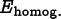 and a
shape
energy,
and a
shape
energy,
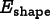 . Their
relative importance is controlled by a parameter α:
. Their
relative importance is controlled by a parameter α:
When 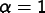 then
then Skeleton modifications that use
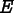 will not consider the shape of
elements at all, and will result in homogeneous but badly
shaped elements. When
will not consider the shape of
elements at all, and will result in homogeneous but badly
shaped elements. When 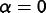 , modifications will not
consider homogeneity, and will result in well shaped but
possibly inhomogeneous elements. When
, modifications will not
consider homogeneity, and will result in well shaped but
possibly inhomogeneous elements. When 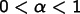 ,
there will be a trade-off between shape and homogeneity.
,
there will be a trade-off between shape and homogeneity.
The homogeneity energy is simply one minus the homogeneity, so that it is minimized when an element is completely homogeneous.
Finite elements are usually better behaved (the resulting matrix equations are easier to solve) if the elements do not have sharp angles or high aspect ratios. The shape energy function returns 0 for equilateral triangular or square quadrilateral elements, and 1 for elements that are degenerate (ie, have an aspect ratio of 0 or three collinear vertices).
The explicit expression for triangular elements is
where 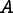 is the area of the
element and
is the area of the
element and 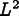 is the sum of
the squares of the lengths of its sides.
is the sum of
the squares of the lengths of its sides.
For quadrilateral elements the shape energy is found by
first computing a “quality factor”,
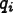 , for each corner
, for each corner
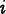 .
.
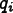 is the area of
the parallelogram defined by the two sides of the element
that converge at node
is the area of
the parallelogram defined by the two sides of the element
that converge at node 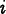 , divided by the
sum of the squares of the sides, and normalized so that
its value is 1 for a square. It's value is always less
than 1 at a corner where the two converging edges have
different lengths or meet at an acute or obtuse angle, and
is zero in the degenerate cases when the edges are
colinear or when the length of one edge is 0. The shape
energy is defined to be
, divided by the
sum of the squares of the sides, and normalized so that
its value is 1 for a square. It's value is always less
than 1 at a corner where the two converging edges have
different lengths or meet at an acute or obtuse angle, and
is zero in the degenerate cases when the edges are
colinear or when the length of one edge is 0. The shape
energy is defined to be
where 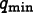 is
the minimum (worst)
is
the minimum (worst) 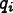 in the element,
in the element,
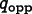 is
the
is
the 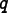 at the opposite
corner, and
at the opposite
corner, and  is a small
number. (The
is a small
number. (The  term is
required to prevent pathologies that occur when the shape
energy has no dependence on the position of one of the
nodes.
term is
required to prevent pathologies that occur when the shape
energy has no dependence on the position of one of the
nodes.  is set to
1.e-5 in the program, but its exact value is
inconsequential.)
is set to
1.e-5 in the program, but its exact value is
inconsequential.)
The nodes at the corners of an element are ordered. The perimeter of the element is traversed counterclockwise when moving from one node to the next. Any operation that breaks this ordering makes the element illegal. Elements with three collinear nodes are also illegal, as are non-convex quadrilaterals. (Such elements introduce singularities and instabilities in the finite element stiffness matrix.) Figure 2.5 illustrates how node motion may create illegal elements.
Most Skeleton tools will refuse to create illegal
elements. The one exception is the Move Node
toolbox, which allows the user to move nodes by hand.
Sometimes it may be necessary to temporarily make an illegal
element while moving a bunch of nodes.
Figure 2.5. Creating Illegal Elements
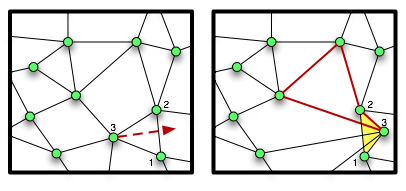
Moving the node in the left hand figure results in two illegal elements in the right hand figure. The shaded triangle is illegal because its nodes (numbered 1,2,3) are out of order. The highlighted quadrilateral is illegal because it is not convex.
The nodes of a Skeleton element are the
corners of the element, as shown in Figure 2.3. Unlike real finite
elements, Skeleton elements may not have nodes along
their edges or in their interiors.
Many Skeleton operations operate on the set of currently
selected nodes. Nodes may be selected by the Skeleton Selection
Task Page and the Skeleton
Selection toolbox.
Node Mobility.
Nodes may be moved when a Skeleton is modified.
Different nodes have different degrees of mobility. The
Nodes at the four corners of a Microstructure can never move. The
Nodes along the edges of a Microstructure can move along the edge,
but cannot move into the interior. All the interior Nodes
can move freely (see Figure 2.6).
In addition, any Node may be explicitly pinned
to prevent it from moving at all.
The segments of a Skeleton are the edges of
the elements, i.e, the lines
joining the nodes. (See Figure 2.3.)
Many Skeleton operations operate on the set of currently
selected segments. Segments may be selected by the Skeleton Selection
Task Page and the Skeleton
Selection toolbox.
Segment Homogeneity.
Homogeneity can be computed on Segments just as it can on
Elements. Analogous to the definition of Element homogeneity,
the homogeneity of a Segment is defined as the fraction of
the length of the segment that lies above that Segment's
dominant pixel type. See Figure 2.7 for a graphical
representation.
Figure 2.7. Homogeneity of Segment
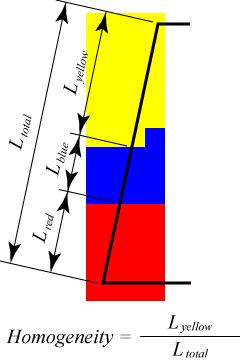
Yellow is the dominant pixel color along the segment. Thus, the homogeneity of the Segment is the ratio of the fractional length covered by yellow pixels along the Segment Lyellow/Ltotal.
The components of a Skeleton, elements,
nodes,
and segments,
may be placed into named groups. These groups form a
convenient way to save and recover sets of selected objects.
Groups are created and manipulated by the Skeleton Selection
Task Page.
Skeleton boundaries define the places where
boundary
conditions will be applied when solving equations on a
Mesh. The Mesh inherits its boundaries from its Skeleton.
There is no way to create boundaries in a Mesh directly.
Boundaries may coincide with the perimeter of the Skeleton, but
there is no requirement that they do so.
Boundaries are created and manipulated by the Skeleton Boundaries task page.
Edge boundaries are composed of directed sets of conjoined
segments. Each
Skeleton automatically contains edge boundaries named
top, bottom,
left, and
right. Dirichlet,
Neumann,
and Floating
boundary conditions may be applied at edge boundaries.
Point boundaries consist of sets of nodes. Each
Skeleton automatically contains point boundaries named
topleft,
topright,
bottomleft, and
bottomright. Dirichlet,
Floating, and
Generalized
Force boundary conditions may be applied at point
boundaries.


![\[E = \alpha E_\mathrm{homog.} + (1-\alpha)E_\mathrm{shape} \]](equations/2.4.2.2-eq-1.gif)
![\[ E_\mathrm{shape} = 1 - 4\sqrt{3}\frac{A}{L^2} \]](equations/2.4.2.2.2-eq-1.gif)
![\[ E_\mathrm{shape} = 1 - [(1-\epsilon)q_\mathrm{min}
+ \epsilon q_\mathrm{opp}] \]](equations/2.4.2.2.2-eq-2.gif)