OOF2: The Manual

Smooth (Smooth)
Prev  6.5.2. Subclasses  Next

Name

Smooth (Smooth) — Move nodes to the average position of their neighbors and accept ones that meet the acceptance criterion.

Synopsis

Smooth(targets,criterion,T,iteration)

Details

  • Base class: SkeletonModifier

  • Parameters:

    targets
    Which nodes to move. Type: An object of the FiddleNodesTargets class.
    criterion
    Acceptance criterion Type: An object of the SkelModCriterion class.
    T
    Failed moves will be accepted if T>0 and exp(-diffE/T) > r, where diffE is the energy gained and r is a random number between 0 and 1. Type: A real number.
    iteration
    Iteration method. Type: An object of the IterationManager class.

Description

Smooth moves Nodes to the average positions of their neighbors in order to smooth out gradients in Node density in a Skeleton.

Typically, it takes about 3 iterations of Smooth to get desirable result. The general procedure for a single iteration is as follows:

  1. Collect target nodes according to the given targets parameter. The collected Nodes are re-ordered randomly to avoid any potential artifacts from the original ordering of Nodes. This re-ordering is repeated at every iteration.

  2. Give each Node a single chance to move to the average position of its neighbors. For this purpose, neighbors are defined as Nodes that share a Segment with the Node being moved.

    Figure 6.98(a) shows a Node (the red dot) that is about to move to the average position of its neighbors (the green dots).

  3. A node move is accepted only if the move satisfies the specified acceptance criterion. Moved nodes that fail to meet the criterion will spring back to their respective original positions, as shown in Figure 6.59(b).

  4. If the move is unacceptable according to the acceptance criterion, OOF2 may still accept the move if the smoothing is being done at a non-zero temperature. The parameter T sets the effective temperature of the annealing process. Unacceptable moves are accepted with a probability

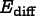    \[P = \exp{(-E_\mathrm{diff}/T)}\] (6.163)

    where \(E_\mathrm{diff}\) is the difference between the effective energies of the new and old Element configurations.

Figure 6.98. Schematics of Smooth

Schematics of Smooth

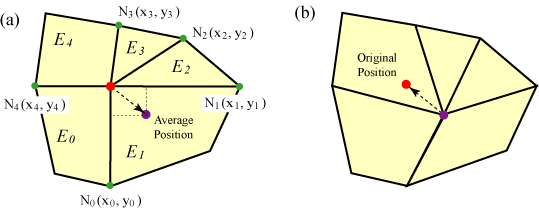
(a) A node moves to its average position with respect to its five neighboring nodes, N0, N1, N2, N3, and N4. The move is affecting its five neighboring elements, E0, E1, E2, E3, and E4. (b) The node moved to its average position. If the move doesn't satisfy the given criterion (computed based on the five affected elements), it'll be rejected.


Smoothing a Skeleton usually requires a number of iterations. The smoothing algorithm converges very quickly, so it's usually sufficient to set the iteration parameter to FixedIteration(iterations=3) to perform exactly three iterations. Nonetheless, it is possible to use conditional iteration, which can repeatedly smooth the Skeleton until the energy drop or acceptance rate per iteration becomes too small.

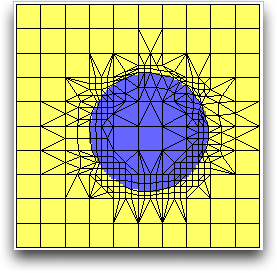
Figure 6.99 shows a Skeleton in which the Elements near the perimeter of the circle have been refined more than those elsewhere, resulting in an uneven Node distribution.

Figure 6.99. Before Smoothing a Skeleton

Before Smoothing a Skeleton

A Skeleton with regions of high node density.


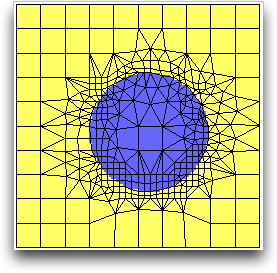
After 3 iterations of smoothing, the Skeleton looks much better in Figure 6.100.

Figure 6.100. After Smooth

After Smooth

A better Skeleton after smoothing.


Statistics for each step of the smoothing process are printed in the OOF2 Message window. For example, 

Iteration 1: E = 1.0480e+02, deltaE=-2.6308e+00 ( 2.510%), Acceptance Rate = 55.3%
Iteration 2: E = 9.0358e+01, deltaE=-9.1959e-01 ( 1.018%), Acceptance Rate = 47.9%
Iteration 3: E = 8.5505e+01, deltaE=-2.0926e-01 ( 0.245%), Acceptance Rate = 40.1%
Iteration 4: E = 8.4485e+01, deltaE=-3.1806e-02 ( 0.038%), Acceptance Rate = 37.2%
Iteration 5: E = 8.4317e+01, deltaE=-3.5836e-03 ( 0.004%), Acceptance Rate = 35.6%

The listing shows the iteration number, the total energy (E) of the Skeleton, the absolute change in energy (deltaE) during the iteration, the percentage change in energy, and the move acceptance rate. If the change in energy or the acceptance rate gets too small, the smoothing process is not being effective at improving the Skeleton. Notice in the example that the energy change per step is decreasing exponentially, indicating rapid convergence.

Prev  Up  Next
Selected Segments (SkeletonSegmentSelectionDisplay)  Home  All Nodes (SnapAll)