OOF2: The Manual
The OOF2 Mesh object represents an actual finite element
Mesh. It combines the geometry of a Skeleton with information
about equations and
boundary conditions, and it stores the values of Fields. In
OOF2 version 2.1 and later, the Mesh can store sets of
Field values, with a different time for each set.
Every Mesh is derived from a Skeleton. The Mesh elements have
the same shape and position as the associated Skeleton elements.
The Material assigned to each Mesh element is the Material
of the dominant pixel
category of its Skeleton element. A single Skeleton may give
rise to more than one Mesh.
Mesh elements are analogous to Skeleton elements,
but they contain more information. In particular, Mesh
elements can perform finite element
interpolation by means of shape
functions. The shape functions form a basis for
the expansion of functions on the mesh, just as the series
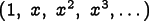 forms a basis for the
expansion of functions of a real number
forms a basis for the
expansion of functions of a real number  . That is, any
function
. That is, any
function 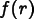 , where
, where
 is a point in
the plane, can be approximated by the sum
is a point in
the plane, can be approximated by the sum
where 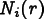 is the
ith shapefunction and
is the
ith shapefunction and
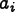 is its
coefficient. In finite elements, the shape functions are
defined so that
is its
coefficient. In finite elements, the shape functions are
defined so that
for some position
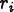 , and
, and
for all 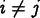 . Therefore, the
coefficients are simply given by
. Therefore, the
coefficients are simply given by
These special positions
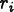 are called the
nodes of the mesh.[5]
There are always nodes at the corners of an element, so the
nodes of a
are called the
nodes of the mesh.[5]
There are always nodes at the corners of an element, so the
nodes of a Skeleton element always correspond to nodes of a
Mesh element, but a Mesh element may have nodes along its
edges or even in its interior.
The above equation
means that a Field 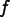 can be determined
by specifying its values
can be determined
by specifying its values
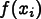 only at the
nodes. Thus we think of the
only at the
nodes. Thus we think of the Field values as living on the
nodes of the mesh. The goal of a finite element solution is
to find Field values at nodes.
Why did we bother to explain all this? OOF2 requires you to
choose what kind of finite elements to use when creating a
Mesh. Different types of elements differ in the shape
functions that they provide and in the number and position of
their nodes.
The polynomial order of the element shape functions determines
the order of the interpolation within the element, and
therefore affects the accuracy of the solution. (Fields
computed with linear shape functions will be constrained to
have constant gradients within elements, for example.)
Because shape functions are 1 at one node and 0 at all others,
the number of nodes along an element edge determines the order
of the shape functions: an edge with nodes only at its
endpoints must have linear shape functions, whereas an edge
with nodes at its endpoints and one more in its interior must
have quadratic shape functions.
There are actually three kinds of nodes: nodes used to store
Field values (function nodes), nodes
used to determine the element geometry
(mapping nodes), and nodes used for both
purposes. (Nodes determine element geometry by defining a
mapping from a “master” element with a standard
shape and position to the actual element. The mapping nodes
of the master element are mapped to the nodes of the actual
element, and all other points are mapped by using the mapping
nodes' shape functions for interpolation. Non-linear mapping
can produce elements with curved edges.) Elements with the
same number of function and mapping nodes are called
isoparametric. Elements with more
function nodes than mapping nodes are called
subparametric, and elements with more
mapping nodes than function nodes are called
superparametric.
![[Note]](IMAGES/note.png) |
Note |
|---|---|
|
Currently, although OOF2 allows high-order iso- and
superparametric elements with non-linear mapping and
curved element edges, it actually doesn't do anything
useful with them. This is because |
A Mesh may be divided into a number of SubProblems, which
can be solved independently. SubProblems may differ from
one another geographically, by including different Elements.
They may also differ in which Fields and Equations are
defined on them. For example, you might want to solve one set
of equations on particulate inclusions and another set on the
matrix in which they're embedded. Or in a time dependent
problem, you might put the fast and slow degrees of freedom in
separate subproblems and use different solution methods on
each.
When a Mesh is created, a default SubProblem, called
default, is created as well. The
default SubProblem includes the entire Mesh. Users who
don't need to use more complicated SubProblems can simply
use the default, and can more or less forget that
SubProblems exist at all. (Just think “mesh”
when you read “subproblem” and you'll be fine.)
SubProblems are created in the
Subproblem pane in the FE Mesh Task Page. The
various kinds of SubProblems differ in their geographical
extent. A MaterialSubProblem
includes all Elements with a given Material type. A PixelGroupSubProblem includes all
Elements which have a majority of their underlying pixels in a
given PixelGroup. An EntireMeshSubProblem includes all
Elements. There are also boolean SubProblems that are
defined in terms of other existing SubProblems. The full
set is documented in the SubProblemType class.
Fields are the quantities, such as
Temperature and
Displacement, that OOF2 solves
for. Fields have values at all points of the SubProblem or
SubProblems on which they are defined. The Fields &
Equations Task Page in OOF2 is used to change the
status of Fields.
-
A
Fieldthat is defined on aSubProblemhas memory allocated to store its values at the nodes. -
Values of a field that is active
will be found when the
SubProblemis solved. Only definedFieldscan be activated.
If a Field is defined on two or more geographically
overlapping SubProblems on a Mesh, then the Field's
values are the same for each SubProblem whereever the
SubProblems overlap. That is, although Fields are defined
on SubProblems, their values are actually only stored on the
Mesh.
OOF2 can handle scalar Fields (such as
Temperature), vector Fields (such as
Displacement), and even tensor
fields[6]
(such as liquid crystal order parameters).
Each Mesh also contains a time value.
If a time dependent problem has been solved on a Mesh, the
Mesh will store the values of the Fields at the starting
time, the ending time, and possibly, if Outputs have been
scheduled, at intermediate times as well, but there is always
one time and one set of Fields that describe the current
state of the Mesh. The current time can be changed either by
initializing
the Fields or by solving time dependent equations.
OOF2 sometimes needs to store the first time derivative of a
Field. In this case, a new Field will automatically be
created for it. The new Field's name is constructed by
appending _t to the name of the original
Field. For example, Displacement_t
stores the first derivative of
Displacement.
Storing all of the Field values at each time can use a lot
of memory. OOF2 can cache the values either in RAM or in
temporary files on a disk. The cache type for any Mesh can
be changed in the Mesh Operations pane in
the FE Mesh page.
The default cache type, used for new Meshes, can be set in
the OOF.Settings.Mesh_Defaults
menu in the main window's menubar.
In OOF2 a Flux is a quantity analogous to stress in
elasticity: it is generally some modulus times the derivative
of a Field. Some examples are stress (elastic modulus times
the strain, which is the symmetric gradient of the
displacement), heat flux (thermal conductivity times the
negative gradient of the temperature), and electrical
polarization (permittivity times the negative gradient of the
voltage). Properties define how Fields contribute to
Fluxes. One flux may have contributions simultaneously from
many different Properties and Fields.
Fluxes don't appear explicitly when setting up a problem,
except when specifying Neumann or Generalized Force
boundary conditions in the Boundary
Condition page. After obtaining a solution, Fluxes
may be computed for plots or analysis.
OOF2 uses three dimensional material properties but only solves two dimensional problems. In elasticity, two standard ways of reducing three dimensional systems to two dimensions are plane strain and plane stress. Plane strain is implemented by constraining the out-of-plane components of the strain to be zero, and plane stress is (usually) implemented by using an effective in-plane elastic modulus.
OOF2 has to generalize the concepts of plane-stress and
plane-strain because it deals with problems other than
elasticity. Furthermore, since OOF2 allows couplings
between Fields, more than one Field can
contribute to a given Flux, and these couplings are not
known in advance, it is not possible to compute effective
in-plane moduli for generalized plane-stress problems.
OOF2's approach to the out-of-plane problem is to augment
each Field with the out-of-plane
components of its derivatives. For example, scalar Fields
like Temperature become a pair of
Fields, Temperature and
Temperature_z, where
Temperature_z is the z-derivative of
the temperature. Displacement, which
is a two-dimensional vector Field in the plane, is augmented
with Displacement_z, which is the
triplet of partial derivatives
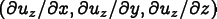 ,
where
,
where
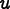 is the (three dimensional) displacement field. Then the
generalization of plane-strain simply sets these out-of-plane
derivatives to zero and excludes them from the solution
process. This is done for
is the (three dimensional) displacement field. Then the
generalization of plane-strain simply sets these out-of-plane
derivatives to zero and excludes them from the solution
process. This is done for Fields that are marked as
in-plane in the Fields &
Equations task page. Note that Fields that are
in-plane in one SubProblem must be in-plane in all
SubProblems.
Plane-stress is generalized by augmenting the system of finite
element equations by plane-flux
equations that constrain the out-of-plane components of the
Fluxes to be zero. This increases the size of the system of
linear equations to be solved, but, unlike the method of
defining effective in-plane moduli, works even if there are
arbitrary couplings between fields.
Activating
Equations in the Fields &
Equations task page determines what physics problem
OOF2 solves. There are (currently) two kinds of equations,
divergence
equations and plane-flux
equations.
Equations are activated and deactivated on SubProblems.
When we say that a SubProblem is solved, we
really mean that its active Equations are solved in the
portion of the Mesh that is included in the SubProblem.
Section 6.4.4 in Chapter 6 lists all of the predefined
Equations in OOF2. Chapter 7
explains how to add new Equations.
Divergence equations are of the form
where 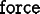 is a generalized force.
Examples are the force balance equation
(
is a generalized force.
Examples are the force balance equation
(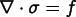 , where f is an actual force) and the heat equation
(
, where f is an actual force) and the heat equation
(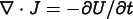 , where the right hand side is
a given rate of change of thermal energy density).
, where the right hand side is
a given rate of change of thermal energy density).
The general form of the time dependent version of the divergence equation is
For first order problems,
e.g. the heat equation, the
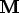 term will be zero. For second order problems the
term will be zero. For second order problems the
 term may be zero.
term may be zero.
Plane flux equations implement OOF2's generalization of plane-stress. They simply state that the out-of-plane components of some flux are zero:
Examples are the plane-stress equation
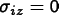 ,
,
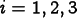 ,
and the plane-heat-flux equation
,
and the plane-heat-flux equation
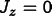 .
.
OOF2 can solve nonlinear versions of Equations (2.8), (2.9), and (2.10), as long as the nonlinearity is
confined to the 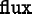 and
and
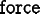 terms.
terms.
The exact form of the Equations that OOF2 solves is
determined by a number of things:
-
The
Equationsmust be activated, or they won't be solved. -
If the
MaterialscontainPropertiesthat contribute to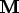 or
or  , then the time
dependent version of equation (2.9) will be solved instead
of the static version (2.8).
, then the time
dependent version of equation (2.9) will be solved instead
of the static version (2.8).
-
However, if the
SubProblem's solver is static, the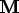 and
and  terms in its
equations will be ignored, even if
terms in its
equations will be ignored, even if Propertiescontribute to them. -
The form of the
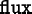 that appears in equations (2.8), (2.9), or (2.10) is determined by the
that appears in equations (2.8), (2.9), or (2.10) is determined by the
Properties. EachEquationinvolves a singleFlux. All of theMaterial'sPropertiesthat contribute to theFluxwill be included, if theFieldsthat thePropertyrequires are defined.For example, if a linear
ElasticityPropertyis the onlyPropertypresent and if theDisplacementFieldis defined, then the stress flux (which is flux for the Force Balance equation) will be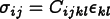 . If a
Thermal
Expansion
. If a
Thermal
Expansion Propertyis present as well andTemperatureis also defined, the stress will be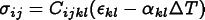 .
.
OOF2 provides five kinds of boundary conditions, Dirichlet, Neumann, Floating, Generalized Force and Periodic.
They can be applied only at boundaries
that have been defined in the Skeleton from which the Mesh was
derived. The Fields and Equations referred to in the
boundary conditions need to be active.
-
A Dirichlet boundary condition specifies the value of one component of a
Fieldalong a boundary. -
A Neumann boundary condition specifies the normal component of a
Fluxon a boundary. -
A Floating boundary condition is like a Dirichlet condition, except that the
Fieldvalues along the boundary can vary by an unknown offset, which will be solved for. That is, if the condition specifies that the field values are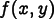 ,
the actual values will be
,
the actual values will be
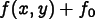 where
where
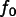 is unknown, but has the same value at all points on the
boundary.
is unknown, but has the same value at all points on the
boundary.
-
A Force boundary condition specifies the generalized force on each
Nodein the boundary. It is a discrete version of a Neumann condition, appropriate if you really have point sources of mechanical force or heat flux, for example. -
A Periodic boundary condition specifies that a component of a
Fieldon the boundary has the same value as theFieldon the boundary on the opposite side of the system. Periodic boundary conditions can only be applied toMeshesbuilt from periodicSkeletons.
The Boundary Conditions Task Page contains the GUI for constructing and manipulating boundary conditions. The underlying commands are in the OOF.Mesh.Boundary_Conditions menu. The boundary condition objects themselves are in the BC class.
Boundary conditions may be explicitly enabled or disabled after they've been defined, using the button on the Boundary Conditions page. This allows you to switch back and forth easily to see the effects of different boundary conditions on a solution.
![[Note]](IMAGES/note.png) |
Note |
|---|---|
|
If you are using non-trivial |
A Profile object describes the
shape of a boundary
condition. That is, a boundary condition fixes some
quantity (a Field component, for example) on a boundary
and the Profile of the boundary
condition specifies how that quantity varies along the
length of the boundary.
There are three kinds of Profiles,
used by different kinds of boundary conditions. The
graphical user interface takes care of selecting the right
kind for you, but if you edit scripts, you need to use the
correct type:
-
Subclasses of ProfileX are
Profilesthat vary in position but not in time. They're used in Floating boundary conditions. -
Subclasses of ProfileXT are
Profilesthat can vary in time as well as position. They're used in Neumann and Force boundary conditions. -
Subclasses of ProfileXTd are also
Profilesthat can vary in time and position, but if they vary in time, the time derivative must be provided. They're used in Dirichlet boundary conditions.
In time dependent problems, the initial values of each active
Field must be set. In static linear problems, setting the
initial value is optional, but a good choice of initial value
can help the iterative solvers converge quickly. In static
nonlinear problems, the choice of initial values can affect
the solution.
If the active Equations include second time derivatives,
initial values must also be provided for the Fields' first
time derivatives.
Field initialization is a Mesh-wide operation, and is not
specific to a particular SubProblem. When a Field is
initialized, a value is assigned to it at all Nodes where
the Field is defined.
The initial values of the Fields are set in two steps. In
the first step, the initialization method for each Field is
defined (OOF.Mesh.Set_Field_Initializer).
Initializers can be constants or functions, or they can copy
values from another Mesh. In the second step, all of the
initializers for all of the defined Fields on the Mesh are
applied simultaneously. This step can optionally also set the
Mesh's current time. See OOF.Mesh.Apply_Field_Initializers and
OOF.Mesh.Apply_Field_Initializers_at_Time.
Fields without initializers are unchanged when initializers
are applied. If those Fields have never been solved or
initialized, their values are undetermined, but are probably
zero. It's a good idea to initialize all Fields.
After Materials have been defined and assigned to pixels, a
Mesh has been created, Fields have been defined and
activated, equations have been activated and boundary
conditions have been applied, the next step in solving a
Mesh is to choose a solution method
for each SubProblem. OOF2 lets you choose a solver in one
of two ways:
Both solver modes let you choose a time stepping method. There are three kinds of time steppers:
-
Static steppers don't actually take any time steps, they just solve for the instantaneous values of the
Fieldsat the current time. If theEquationsinclude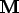 or
or  terms, those terms will be ignored. OOF2 versions
prior to 2.1.0 only included static steppers.
terms, those terms will be ignored. OOF2 versions
prior to 2.1.0 only included static steppers.
-
Uniform steppers take time steps of a fixed size, which you have to specify.
-
Adaptive steppers adjust the size of their time steps in order to keep the estimated error below a given tolerance. You have to specify the tolerance and a minimum allowable step size. Adaptive steppers have to do more computation than uniform steppers on each step, but can often achieve the same accuracy with fewer steps, and therefore are generally preferred.
All of the steppers have to solve a matrix equation at some
point on each step. The matrix has one row for each
Equation component being solved at every Node in the
Mesh, and one column for each Field component at every
Node. Therefore the matrices can be quite large. However,
they are also generally sparse, meaning
that most of its entries are zero. Large sparse matrix
equations are best solved by iterative
methods, which don't require the zeros to be stored
explicitly, but which only provide approximate solutions.
Direct matrix solvers, such as Gaussian
elimination, may give more accurate solutions, but require a
lot more storage and are not suitable for very large problems.
In basic solver mode, you must choose either an iterative or
direct
matrix method. In advanced mode, you have to choose two matrix methods,
for symmetric and asymmetric matrices. The choices include a
number of different iterative techniques and a direct solver.
If the Materials have nonlinear Properties, either the
matrix or the right hand side vector will depend on the
Field values, and a nonlinear matrix solver must be
selected. The nonlinear solvers use the linear solvers, so
you still need to specify a linear matrix method. In basic solver
mode, the nonlinear equations are detected and a nonlinear
solver is chosen automatically. In advanced
mode, you have to select one of OOF2's nonlinear
solvers, Newton and
Picard. Newton uses derivative information
and generally converges faster than Picard, although it requires more
computation per iteration. If the problem is linear, you
should select None for
the nonlinear solver. Picard and Newton will work on linear
problems, but they'll do more work than necessary.
The Solver Page
lets you solve static, quasi-static, and time dependent
systems. Which one it does depends on the solvers that have
been assigned to each SubProblem and on the setting of the
end time with respect to the Mesh's current time:
-
To compute a solution to a static problem, for which static solvers have been chosen for all active
SubProblems, the end time set on the Solver Page must be equal to the current time, or empty. -
To compute the solution to a time dependent problem, adaptive or uniform solvers must assigned to the
SubProblems, and the end time must be set to a time greater than the current time. -
A quasistatic problem is one in which the
Fieldsare completely equilibrated at each time step. To compute a quasistatic solution with OOF2, assign static solvers to theSubProblemsand set the end time to a time greater than the current time.
Time dependent and quasistatic subproblems can be solved
together, by setting the end time greater than the start time,
and assigning a static solver to some SubProblems and an
adaptive or uniform solver to other SubProblems.
The starting time for a time dependent or quasistatic
computation is determined by the initial
conditions. The end time is set by the end
time box in the Solver page. After
solving, a solution may be continued by
increasing the end time and solving again. As long as the
Materials and Equations have not been changed, or the
Fields have not been reinitialized, a continued calculation
is indistinguishable from a calculation that used the new end
time originally.
When multiple SubProblems are being solved, each is
addressed in turn. Because the SubProblems may not be
independent, the whole procedure is iterated until consistent
answers are obtained. For time-dependent problems, this
iteration takes place at every time step. For time-dependent
problems with adapative solvers, the time step will be the
smallest step chosen by all of the solvers.
After solving a Mesh, it's possible to view the resulting
Fields and other quantities that depend on them. These
quantities are generically called
Outputs, and are discussed in Section 6.3. Outputs can be plotted in contour
plots (both plain and
filled)
in the graphics
window, queried at single points with the data
viewer in the Mesh Info toolbox
in the graphics window, or sent through various analysis
routines in the Analysis and Boundary
Analysis pages. The combination of an Output, the
Operations
performed on it, the Domain from which the
data is taken, and the way in which the domain is sampled is called
an Analyis.
Analyses can be scheduled to occur at
particular times during a solution, by using the Scheduled
Output page or the commands in the OOF.Mesh.Scheduled_Output menu.[7] When Outputs are scheduled,
the time stepper will adjust its steps so that it finishes a
step at each output time. Any quantity that can be computed
on the Analysis
or Boundary
Analysis pages can be used as a Scheduled Output.
Operations such as updating the Graphics Window and saving
the Mesh can also be scheduled.
To make it easier to reuse Analyses, they can be given names
on the Analysis
or Boundary
Analysis pages. A Named Analysis can be retrieved and
reused either on the page where it was defined, or as a
Scheduled Output. A Named Analysis defined on one Mesh can
be used on any Mesh on which its Output
is computable and its Domain
is defined.
If a Skeleton is modified, such as by moving Nodes, refining Elements,
defining or removing boundaries,
or undoing or redoing a previous modification, any Meshes
belonging to that Skeleton are declared to be out of
sync, and most operations on the Meshes are
forbidden until the Meshes have been rebuilt. The
rebuilt Mesh will retain all of the SubProblems and boundary
conditions of the old Mesh, and Field values will
be preserved, although they may have to be interpolated onto
the new positions of the Nodes.
A brief description of the state of the current Mesh is
displayed in the Info
pane in the FEMesh
page and in the Status pane of the Solver page. Clicking
the button on the Solver page prints more
information in the Message window.
The status messages are:
-
Unsolved. The
Meshhas been changed in some way since the last time that it was solved, or it has never been solved, but it is ready to be solved. -
Unsolvable. The
Meshcannot be solved for some reason. TheMaterialproperties may be defined inconsistently. There may be activeFieldsthat aren't used in any activeEquations, or activeEquationsto which noPropertiescontribute. The third dimension may not be addressed properly. -
Solved. The
Meshhas been solved, and hasn't been changed since then. -
Failed. A solution was attempted, but it failed for some reason.
-
Out of sync with Skeleton. The
Skeletonhas been changed in some way after theMeshwas created, and theMeshgeometry no longer agrees with it. MostMeshoperations cannot be performed until theMeshis rebuilt.


![\[
f(r) = \sum_i a_i\,N_i(r)
\]](equations/2.5.1-eq-1.gif)
![\[
N_i(r_i) = 1
\]](equations/2.5.1-eq-2.gif)
![\[
N_i(r_j) = 0
\]](equations/2.5.1-eq-3.gif)
![\[
a_i = f(r_i).
\]](equations/2.5.1-eq-4.gif)
![\[
\nabla\cdot\mathrm{flux} + \mathrm{force}
= 0,
\]](equations/2.5.6-eq-1.gif)
![\[
{\bf M}\frac{\partial^2}{\partial t^2}\mathrm{field}
+ {\bf C}\frac{\partial}{\partial t}\mathrm{field}
+ \nabla\cdot\mathrm{flux} + \mathrm{force} = 0.
\]](equations/2.5.6-eq-2.gif)
![\[\mathrm{flux}_z = 0.\]](equations/2.5.6-eq-3.gif)

