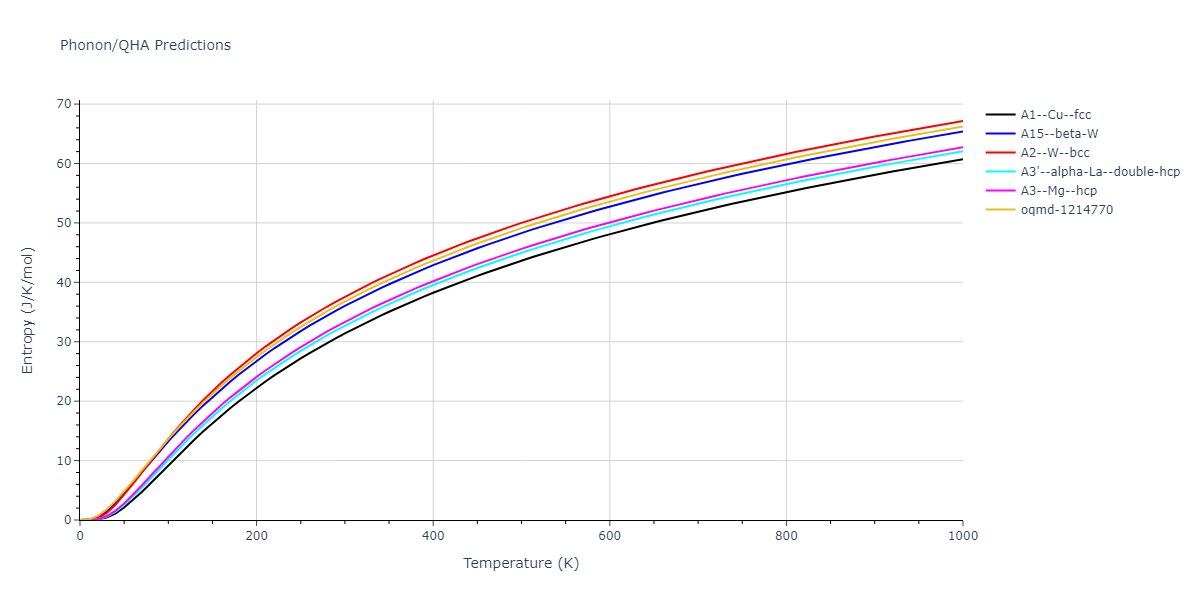
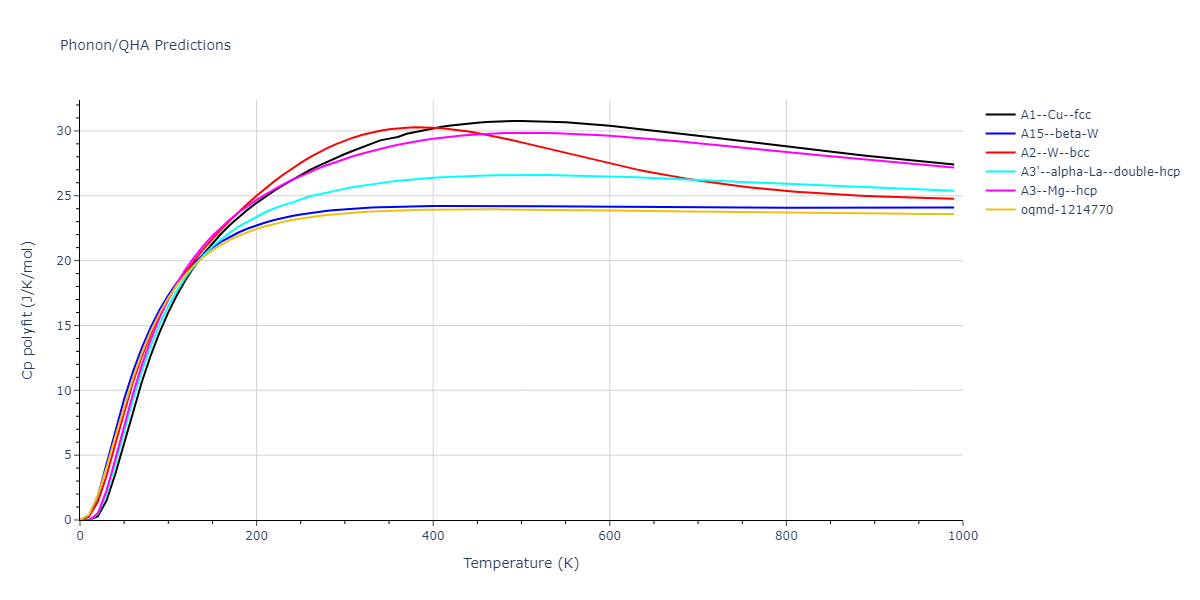
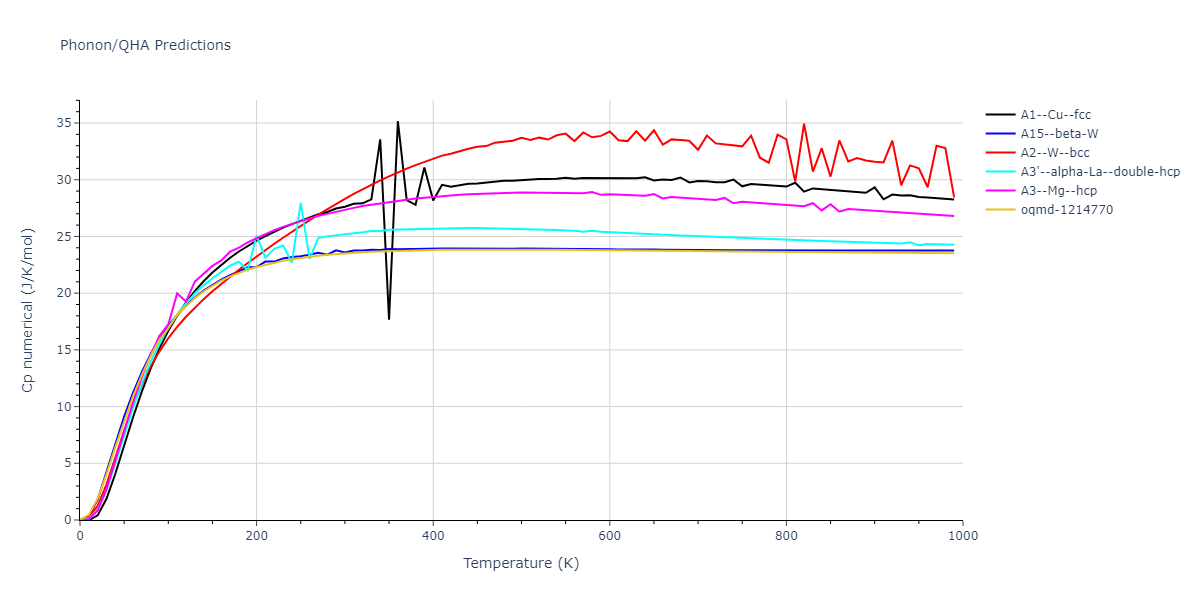
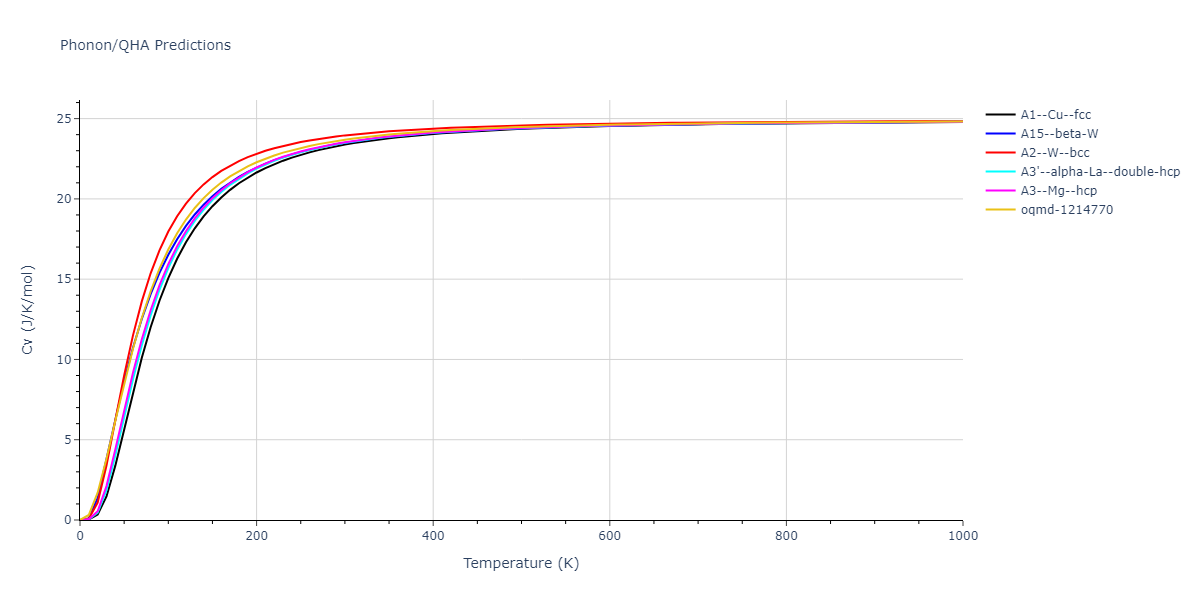
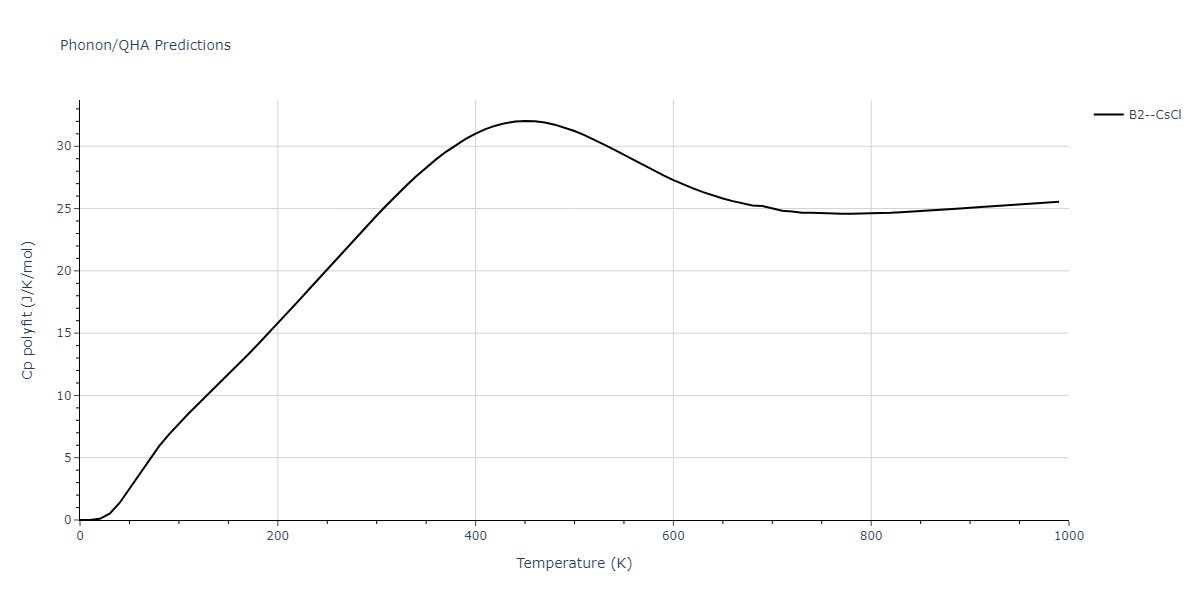
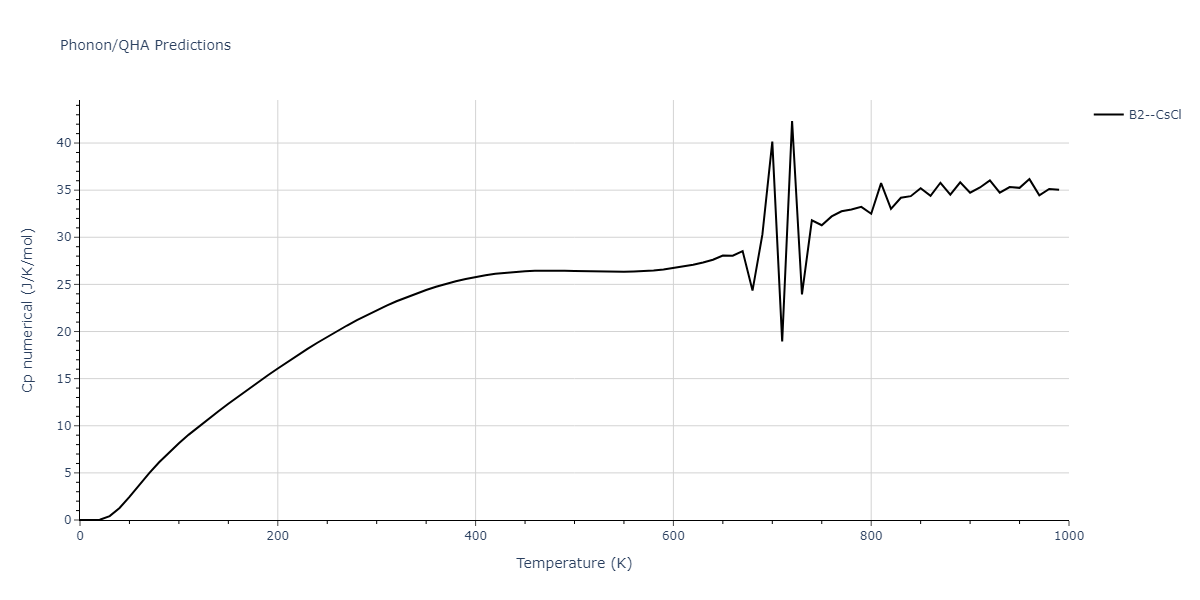
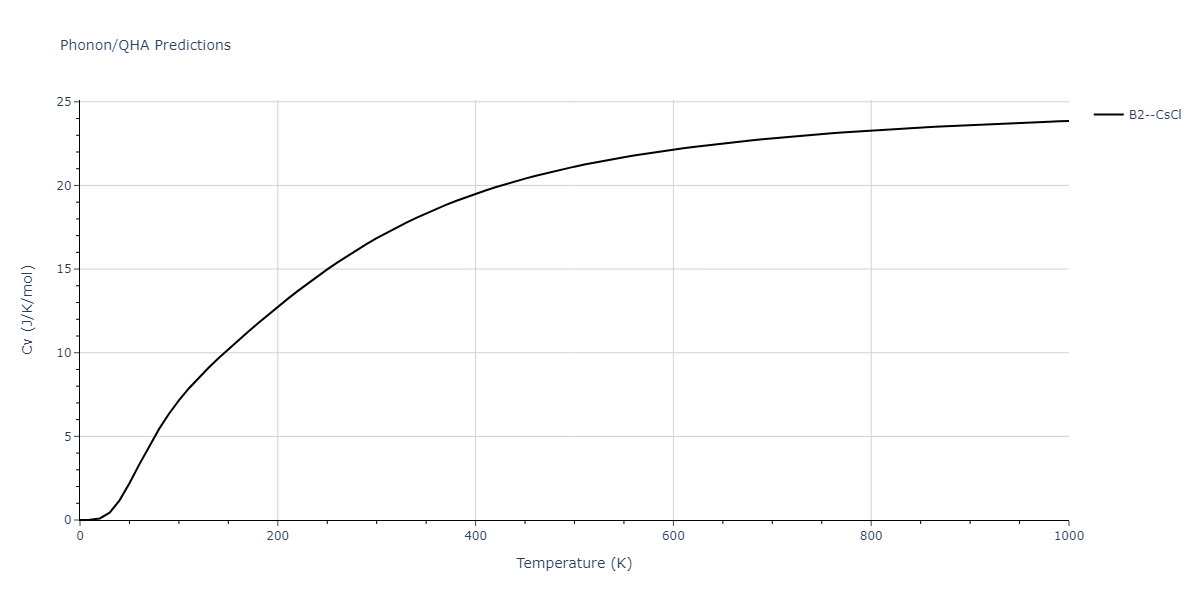
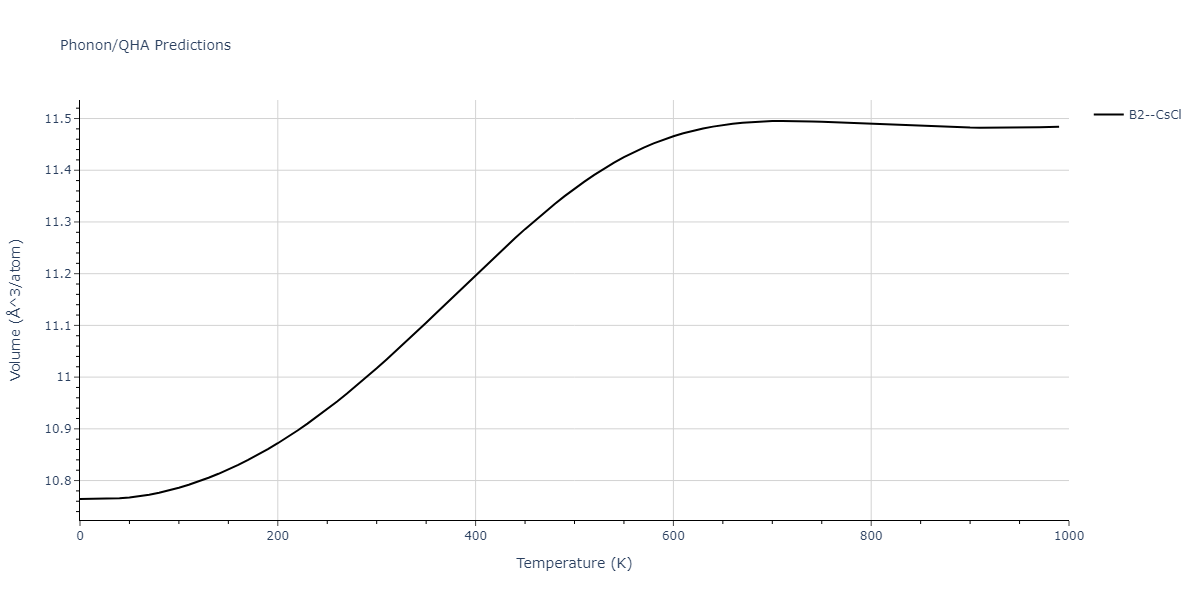
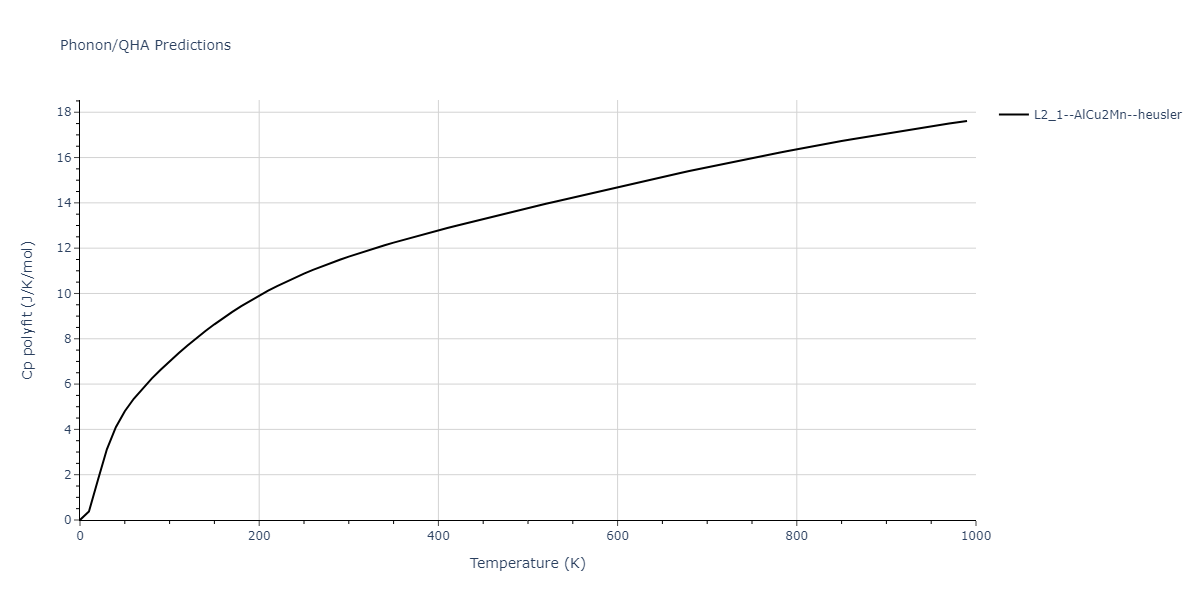
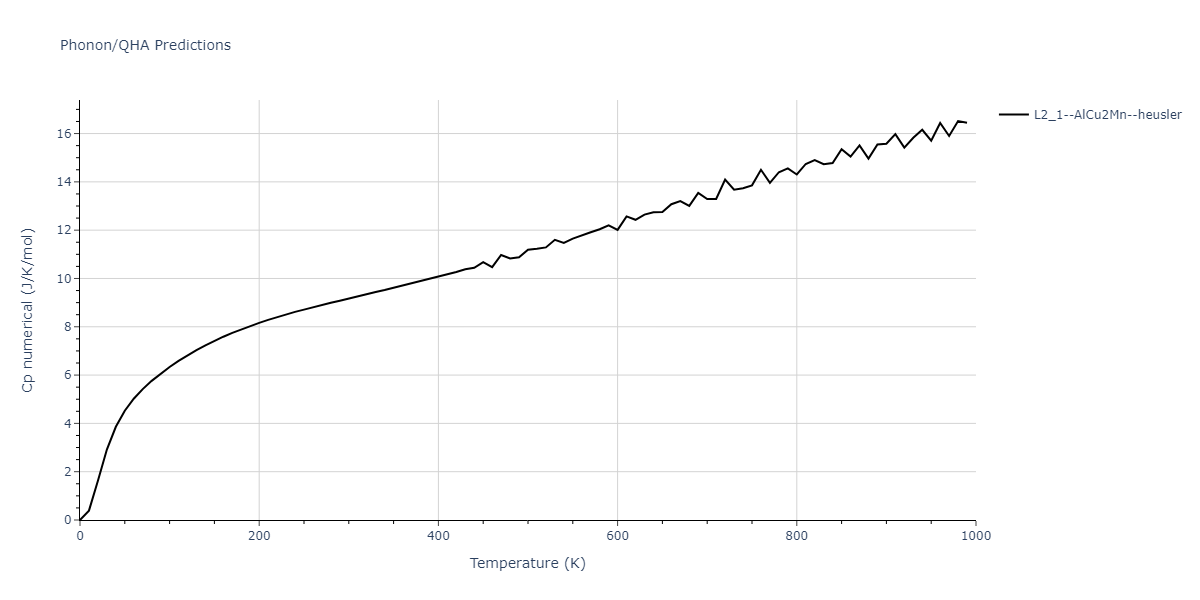
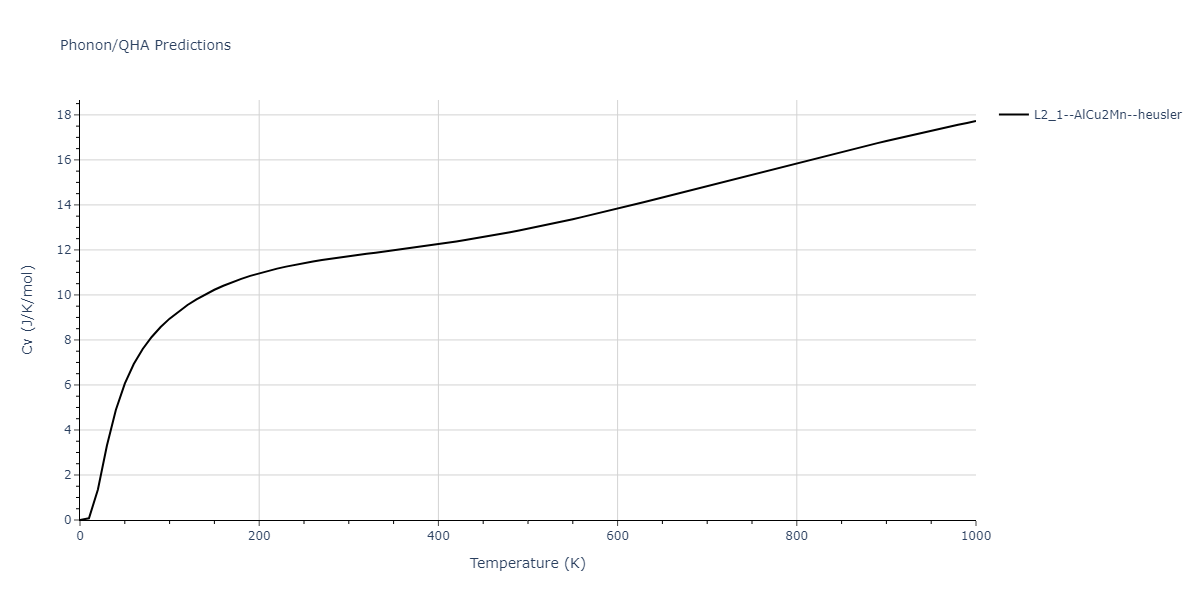
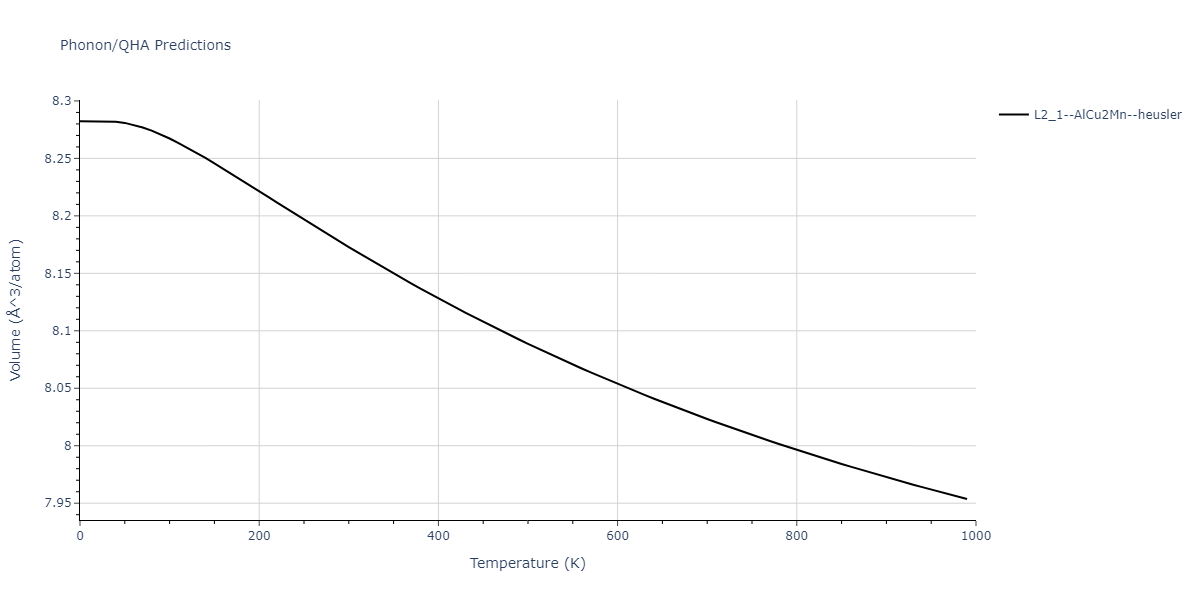
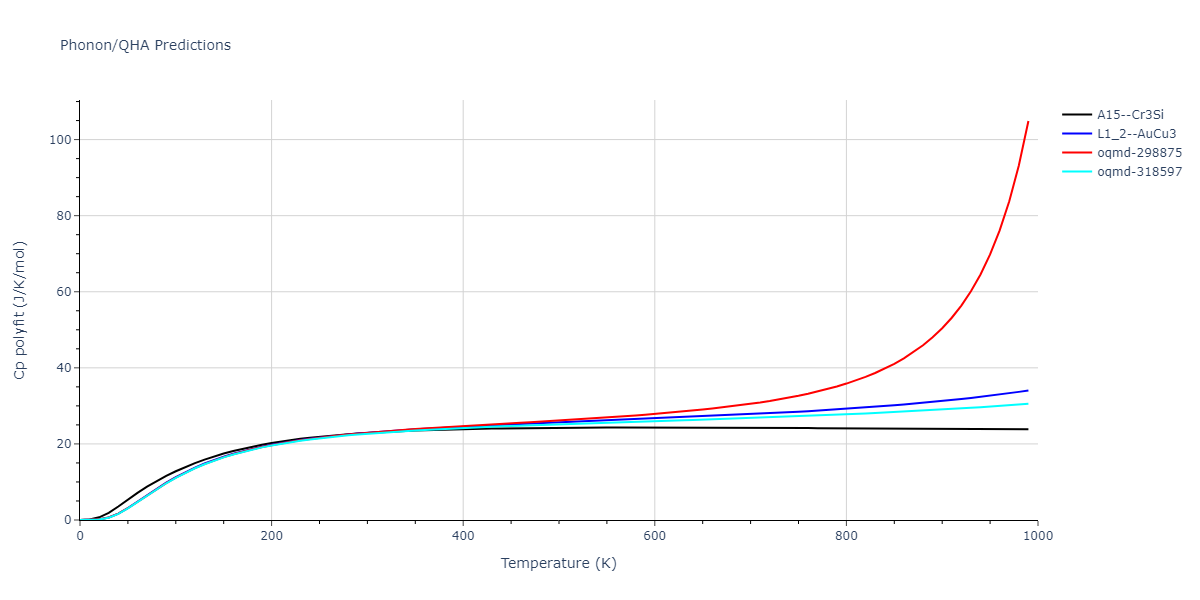
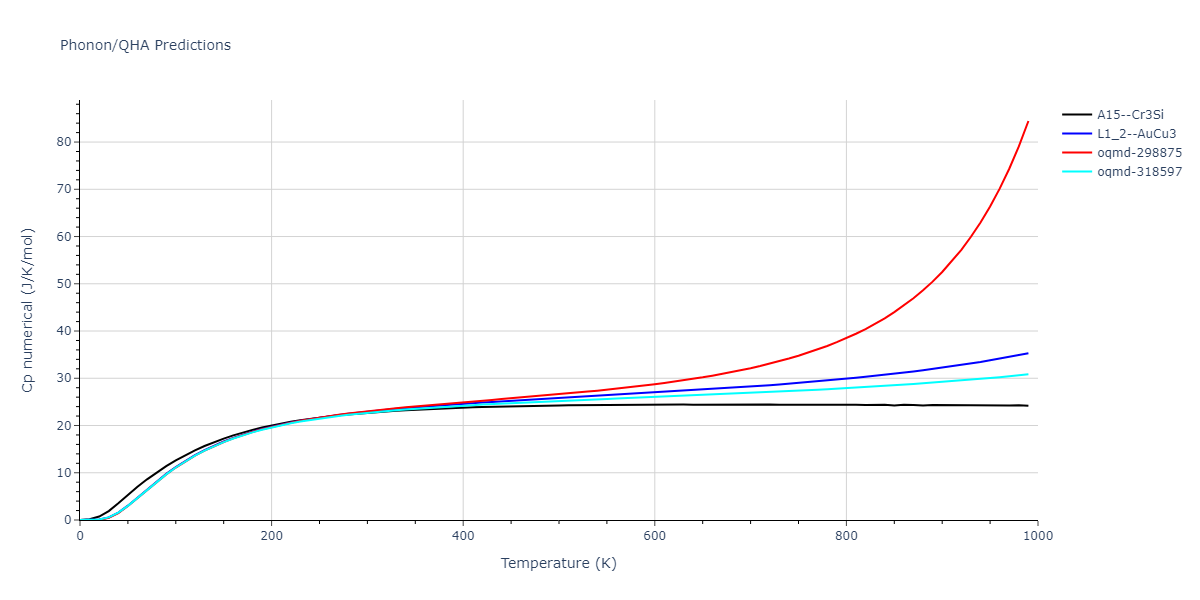
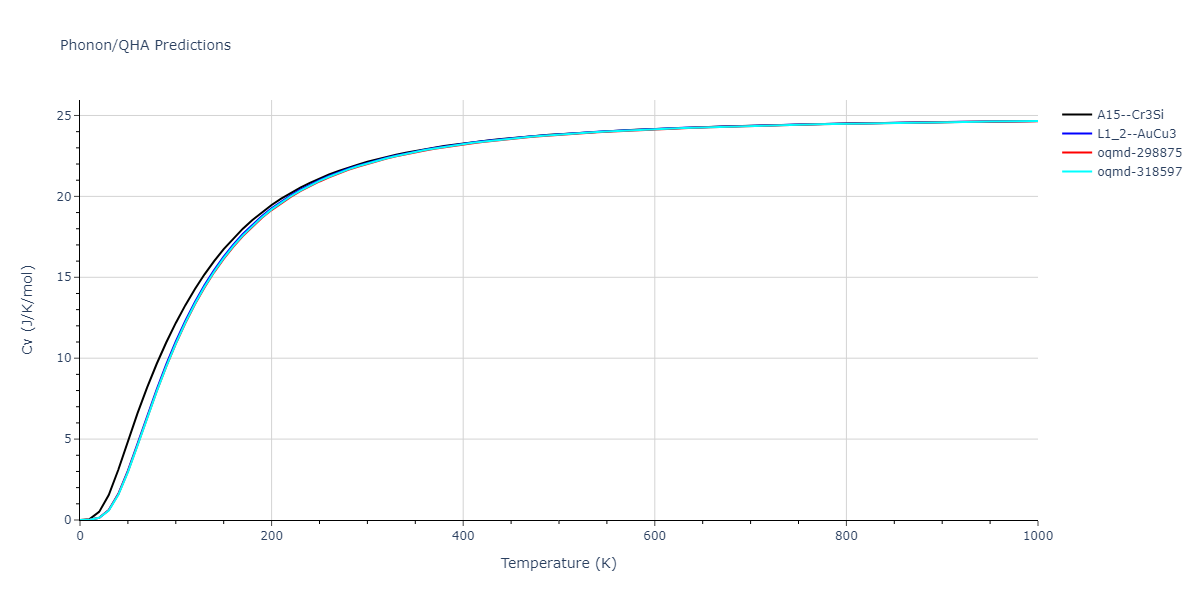
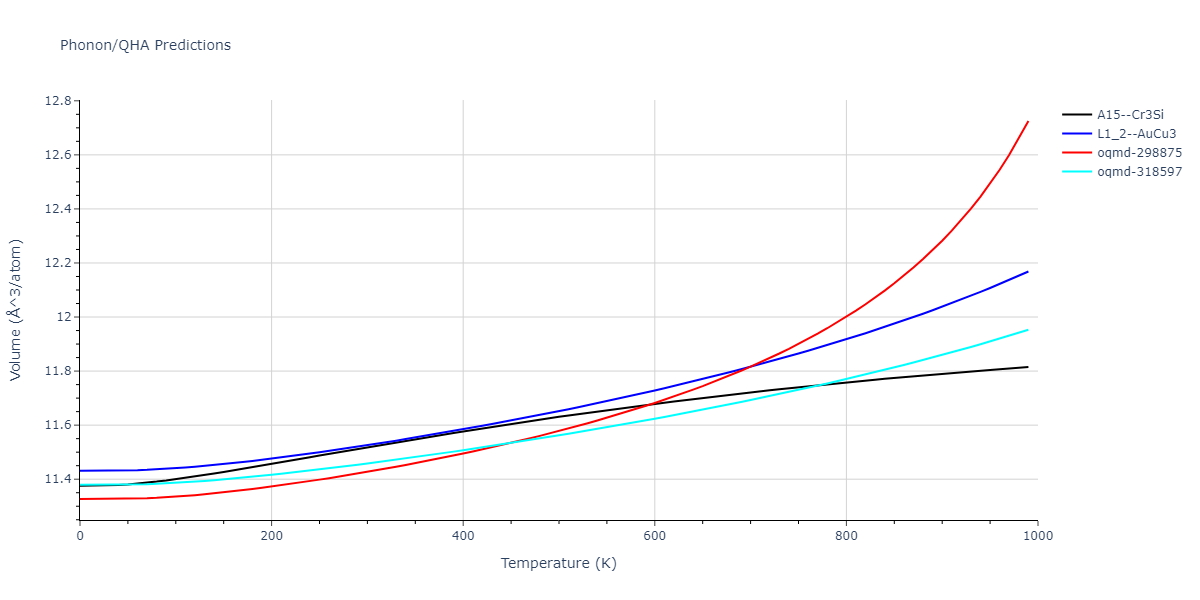
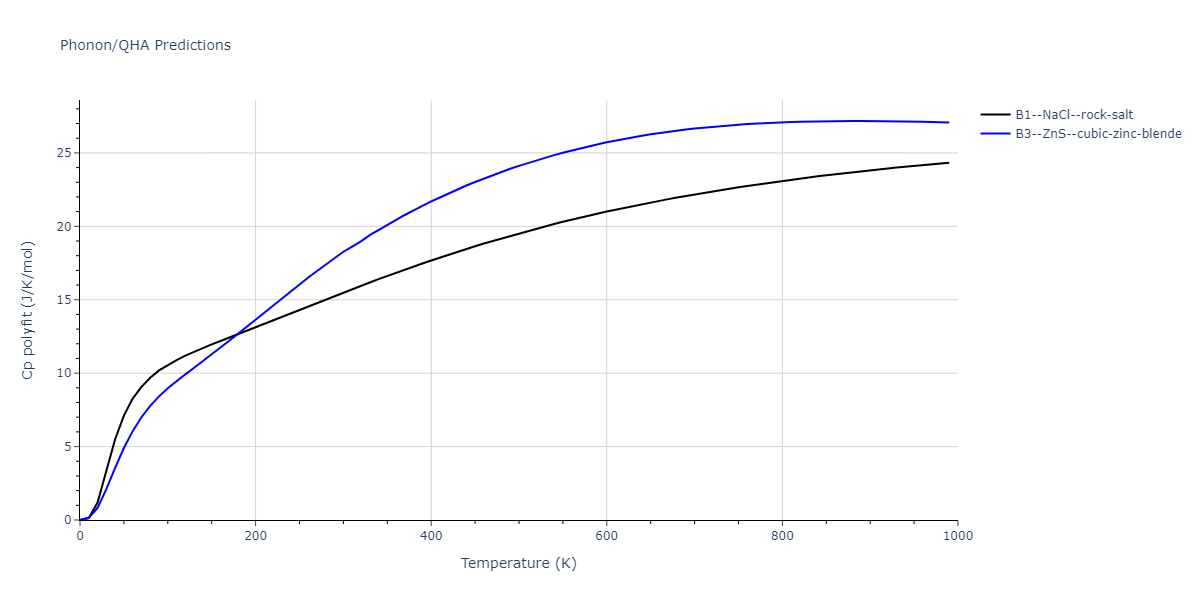
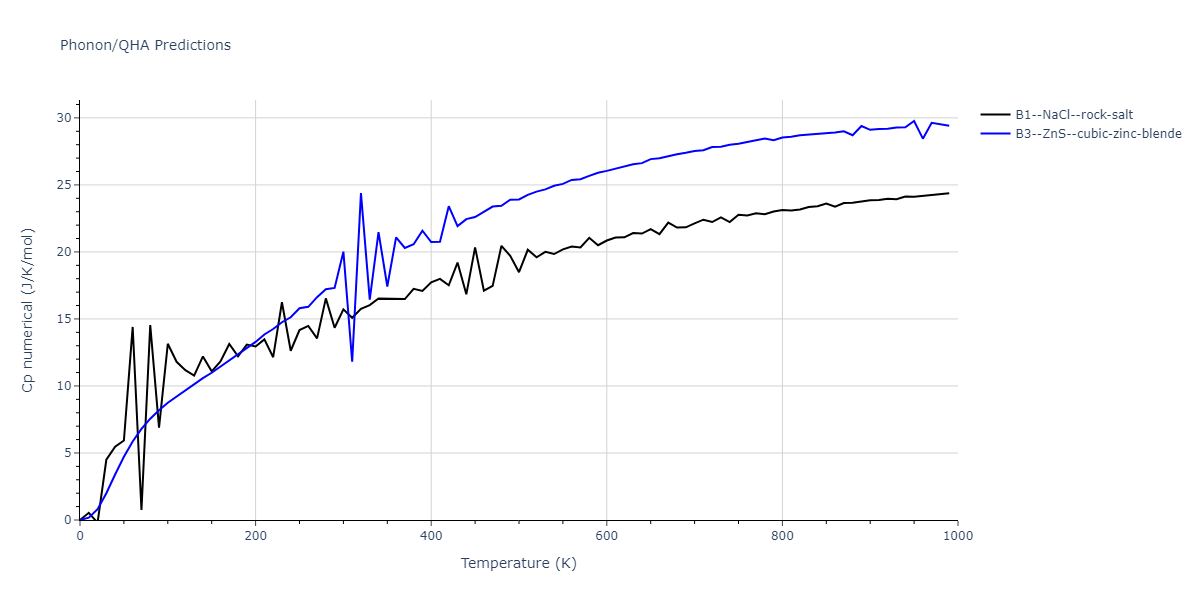
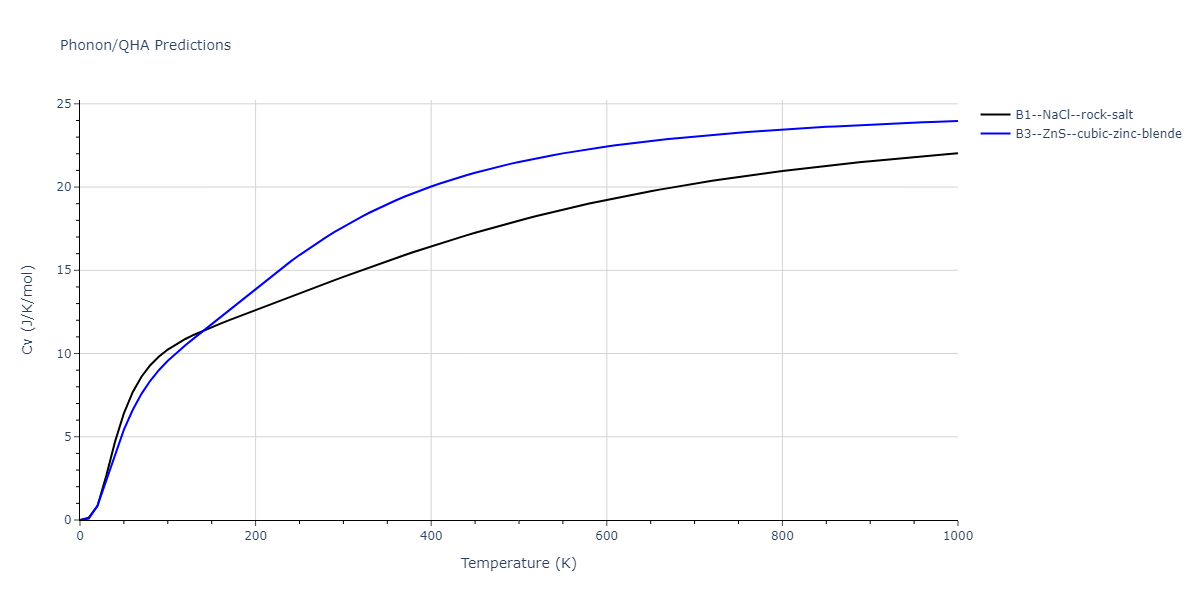
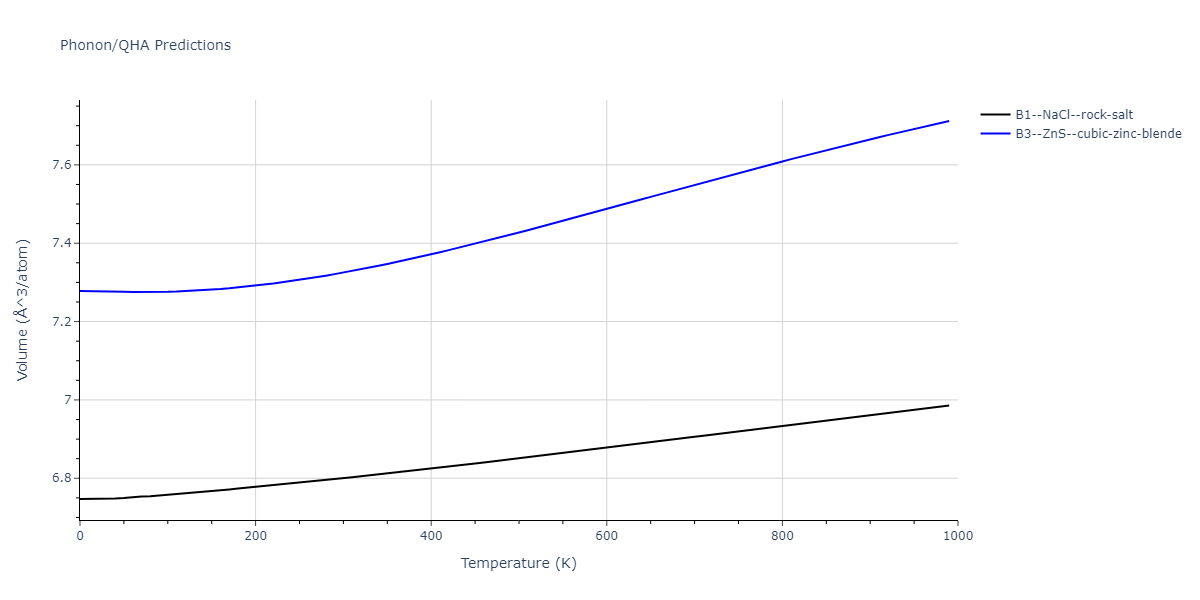
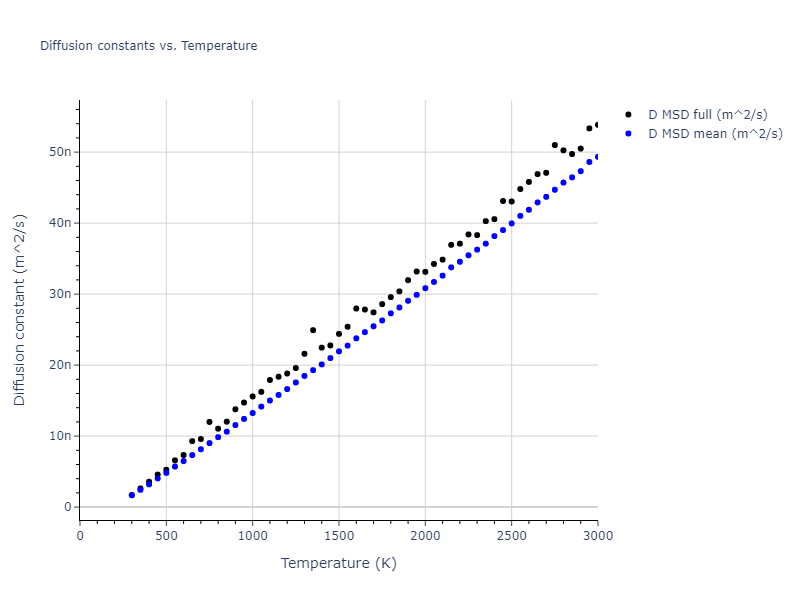
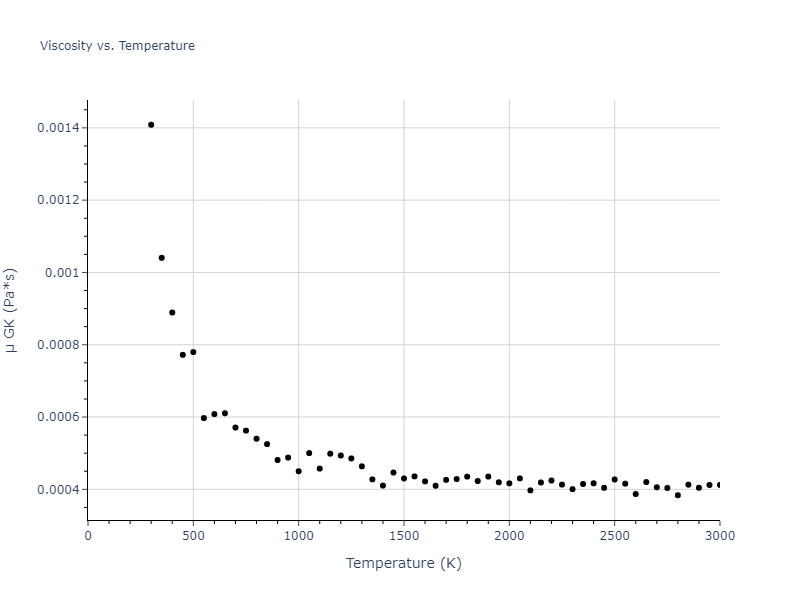
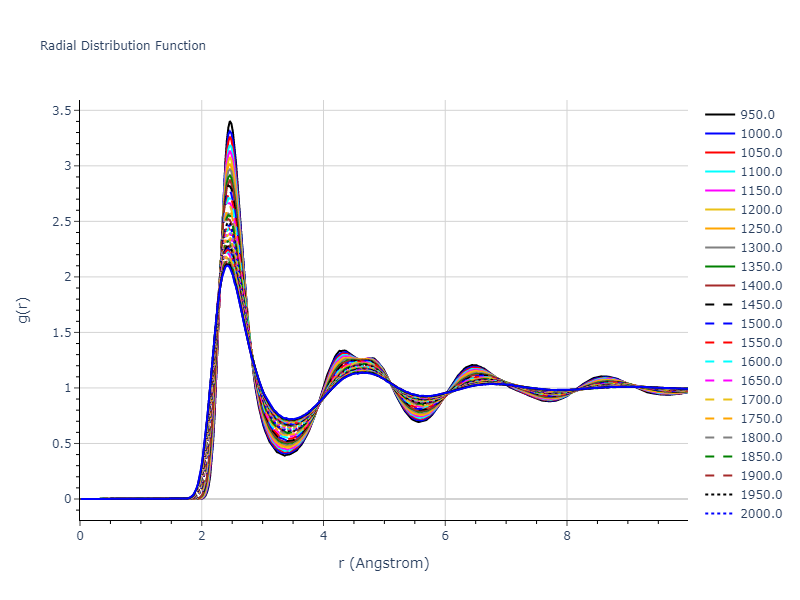
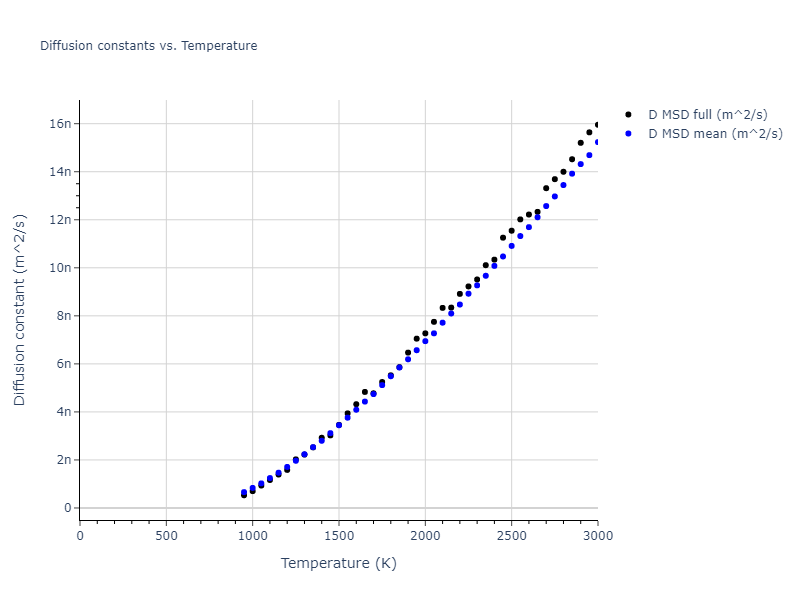
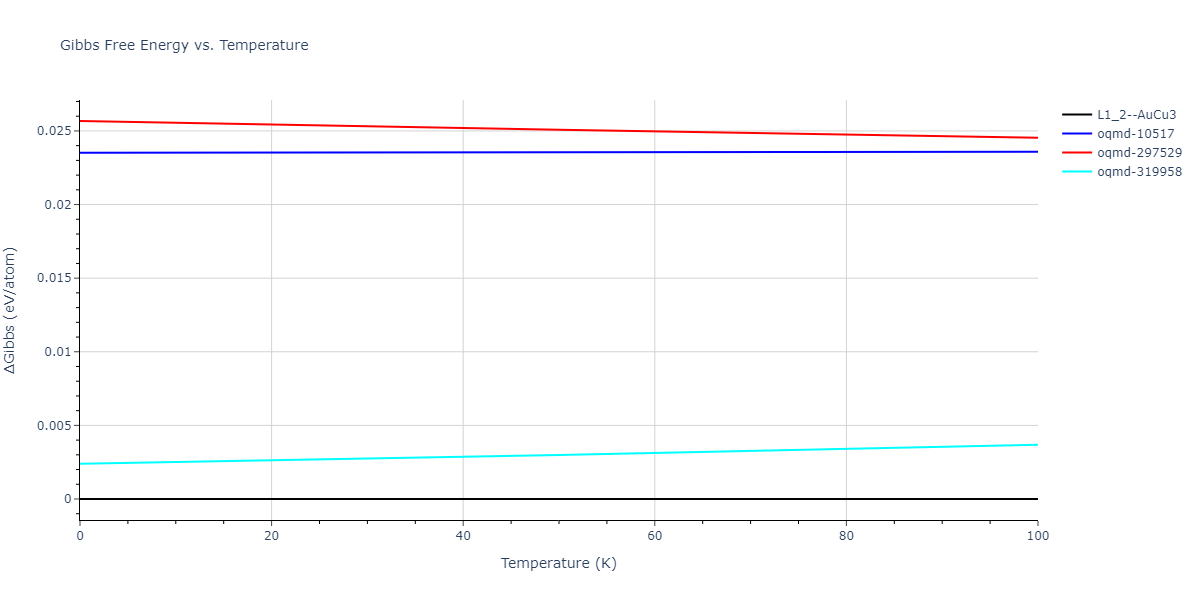
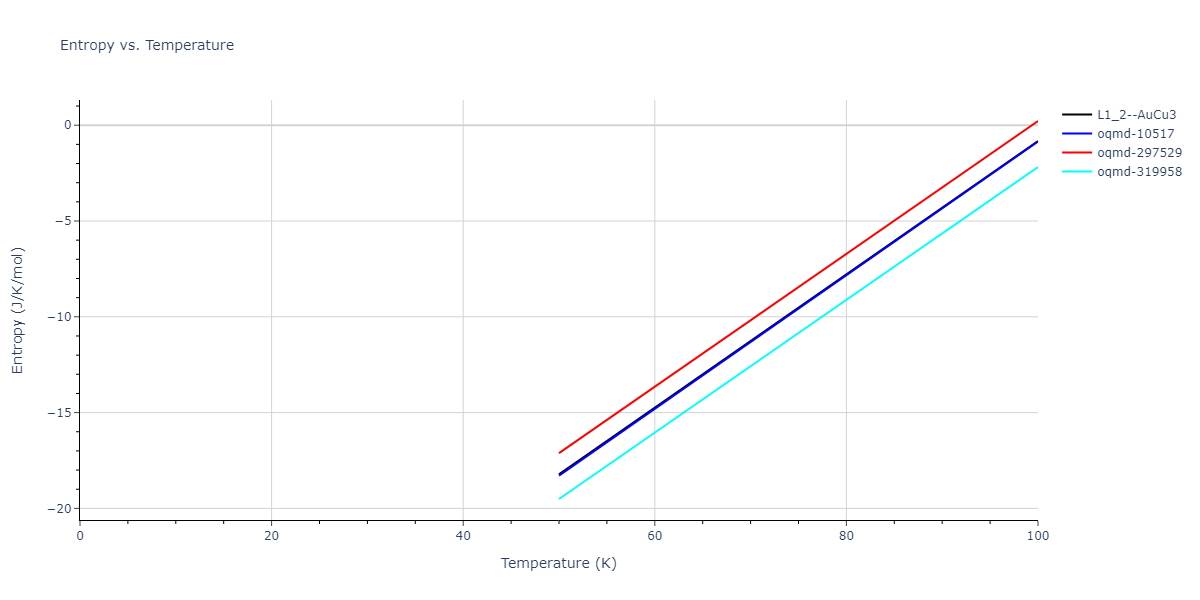
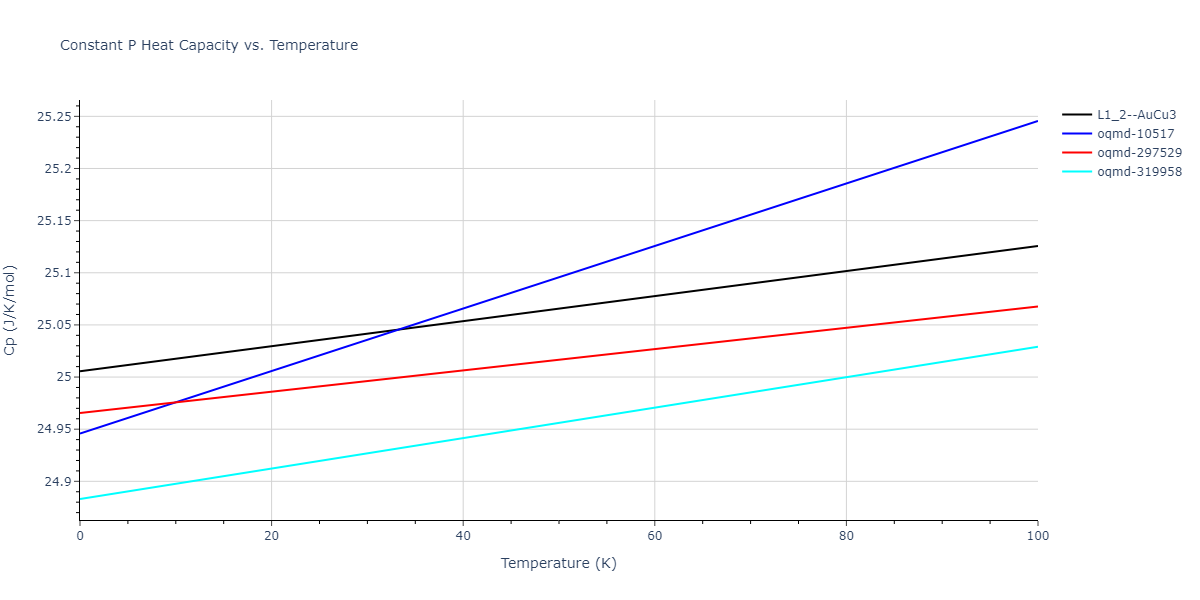
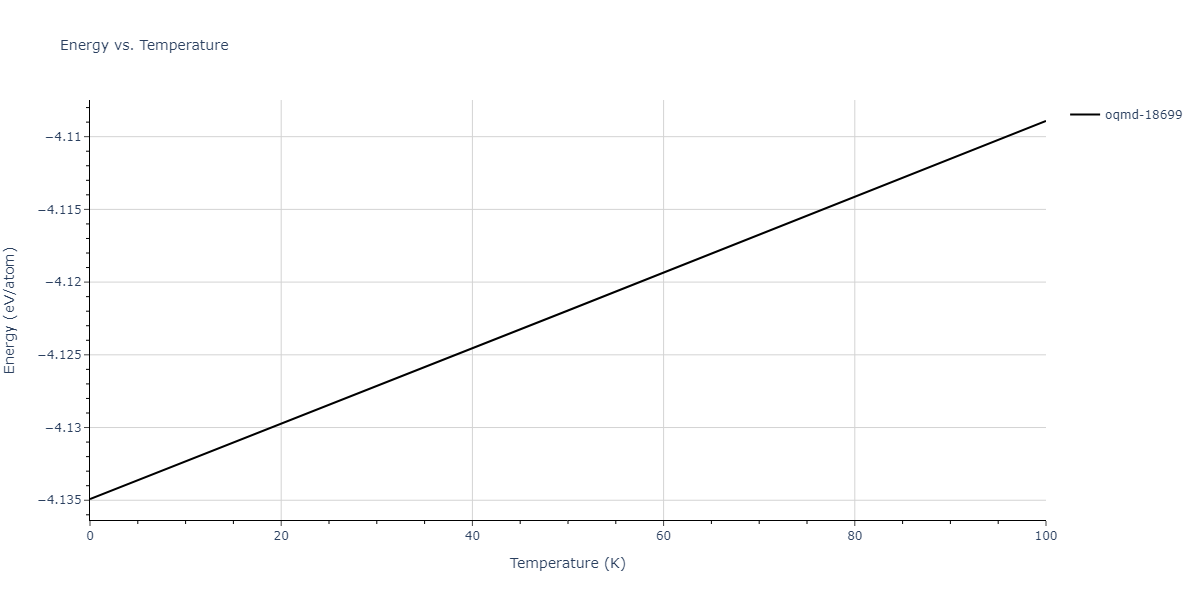
-
Citation: J.E. Angelo, N.R. Moody, and M.I. Baskes (1995), "Trapping of hydrogen to lattice defects in nickel", Modelling and Simulation in Materials Science and Engineering 3(3), 289-307. DOI: 10.1088/0965-0393/3/3/001.Abstract: This paper addresses the energy associated with the trapping of hydrogen to defects in a nickel lattice. Several dislocations and grain boundaries which occur in nickel are studied. The dislocations include an edge, a screw, and a Lomer dislocation in the locked configuration, i.e. a Lomer-Cottrell lock (LCL). For both the edge and screw dislocations, the maximum trap site energy is approximately 0.1 eV occurring in the region where the lattice is in tension approximately 3-4 angstroms from the dislocation core. For the Lomer-Cottrell lock, the maximum binding energy is 0.33 eV and is located at the core of the a/6(110) dislocation. Several low-index coincident site lattice grain boundaries are investigated, specifically the Sigma 3(112), Sigma 9(221) and Sigma 11(113) tilt boundaries. The boundaries all show a maximum binding energy of approximately 0.25 eV at the tilt boundary. Relaxation of the boundary structures produces an asymmetric atomic structure for both the Sigma 3 and Sigma 9 boundaries and a symmetric structure for the Sigma 11 tilt boundary. The results of this study can be compared to recent experimental studies showing that the activation energy for hydrogen-initiated failure is approximately 0.3-0.4 eV in the Fe-based superalloy IN903. From the results of this comparison it can be concluded that the embrittlement process is likely associated with the trapping of hydrogen to grain boundaries and Lomer-Cottrell locks.
Notes: M.I. Baskes provided the reference property calculations in NiAlH_properties.pdf and a list of papers using this potential. If others should be included, please send the citations.- \n
- N.R. Moody, J.E. Angelo, S.M. Foiles, and M.I. Baskes, "Atomistic Simulation of the Hydrogen-Induced Fracture Process in an Iron-Based Superalloy," Sandia National Laboratories Report Number SAND-95-8549C CONF-9510273-1 (1995). \n
- J.E. Angelo and M.I. Baskes, "Interfacial Studies Using the EAM and MEAM," Interface Sci. 4, 47-63 (1996). \n
- M.I. Baskes, J.E. Angelo, and N.R. Moody, "Atomistic calculations of hydrogen interactions with Ni3Al grain boundaries and Ni/Ni3Al interfaces," in A.W. Thompson and N.R. Moody, editors. Hydrogen effects in materials: proceedings of the fifth international conference on the effect of hydrogen on the behavior of materials, Moran, Wyoming, 1994. Warrendale, PA: The Minerals, Metals and Materials Society; 1996. p. 77-90. \n
- J.E. Angelo, N.R. Moody, and M.I. Baskes, "Modeling the segregation of hydrogen to lattice defects in nickel," in A.W. Thompson and N.R. Moody, editors. Hydrogen effects in materials: proceedings of the fifth international conference on the effect of hydrogen on the behavior of materials, Moran, Wyoming, 1994. Warrendale, PA: The Minerals, Metals and Materials Society; 1996. p. 161-170. \n
- M.F. Horstemeyer, M.I. Baskes, and S.J. Plimpton, "Length Scale and Time Scale Effects on the Plastic Flow of FCC Metals," Acta Mater. 49, 4363-4374 (2001). \n
- M.F. Horstemeyer, M.I. Baskes, A. Godfrey, and D.A. Hughes, "A large deformation atomistic study examining crystal orientation effects on the stress-strain relationship," International Journal of Plasticity 18, 203-229 (2002). \n
- S.G. Srinivasan, X.Z. Liao, M.I. Baskes, R.J. McCabe, Y.H. Zhao, and Y.T. Zhu, "Compact and dissociated dislocations in aluminum: Implications for deformation," Phys. Rev. Lett. 94, 125502 (2005). \n
- S.G. Srinivasan, M.I. Baskes, and G.J. Wagner, "Atomistic simulations of shock induced microstructural evolution and spallation in single crystal nickel," J. Appl. Phys. 101, 043504 (2007). \n
- Mei. Q. Chandler, M.F. Horstemeyer, M.I. Baskes, P.M. Gullett, G.J. Wagner, and B. Jelinek, "Hydrogen effects on nanovoid nucleation in face-centered cubic single-crystals," Acta Mat. 56, 95-104 (2008). \n
- Mei. Q. Chandler, M.F. Horstemeyer, M.I. Baskes, G.J. Wagner, P.M. Gullett, and B. Jelinek, "Hydrogen effects on nanovoid nucleation at nickel grain boundaries," Acta Mat. 56, 619-631 (2008).
Related Models: -
LAMMPS pair_style eam/alloy (1995--Angelo-J-E--Ni-Al-H--LAMMPS--ipr1)See Computed Properties
Notes: This file was obtained from the 7 July 2009 LAMMPS distribution and approved by M.I. Baskes.
File(s): -
OpenKIM (MO_418978237058)See Computed Properties
Notes: Listing found at https://openkim.org. This KIM potential is based on the files from 1995--Angelo-J-E-Moody-N-R-Baskes-M-I--Ni-Al-H.
Link(s):
Implementation Information
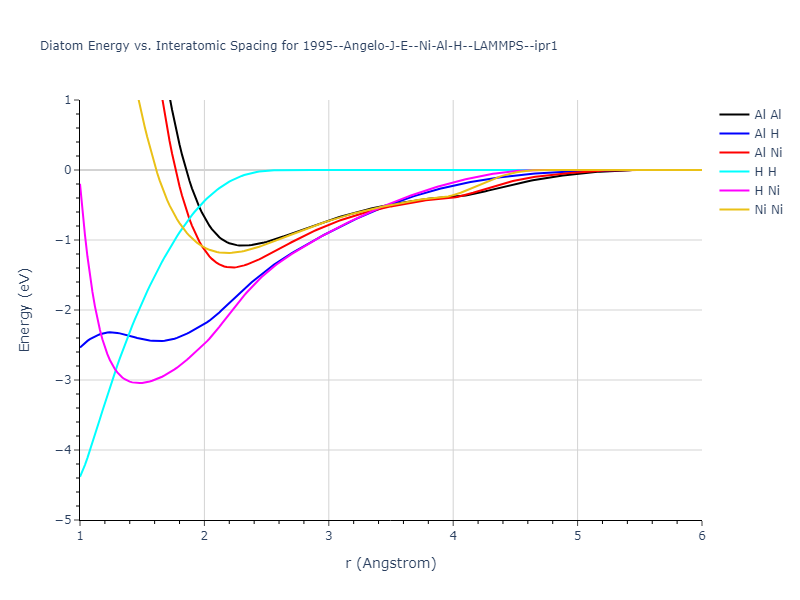
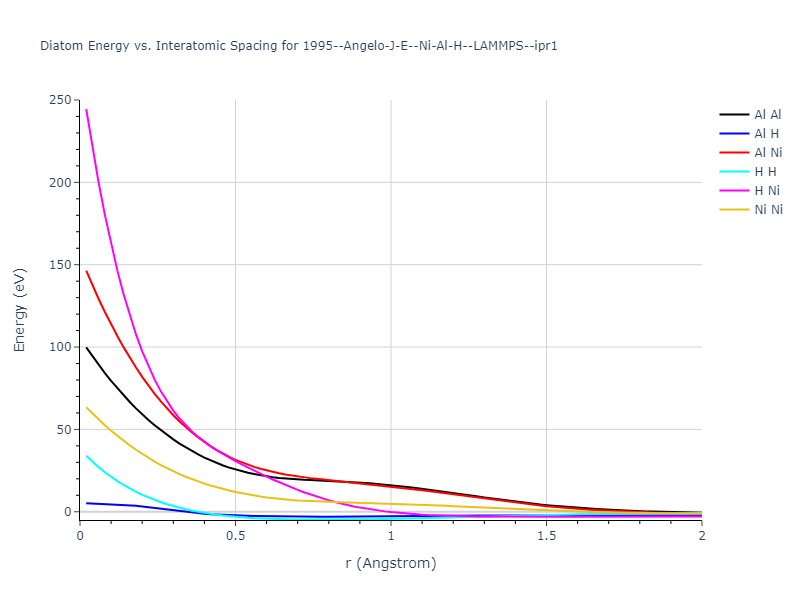
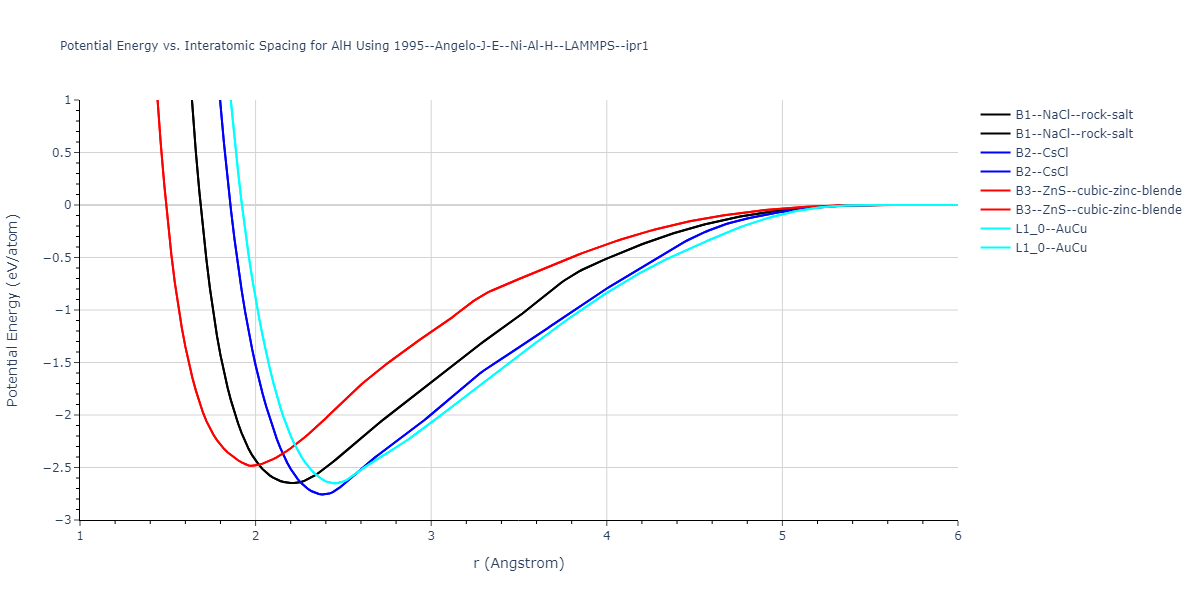
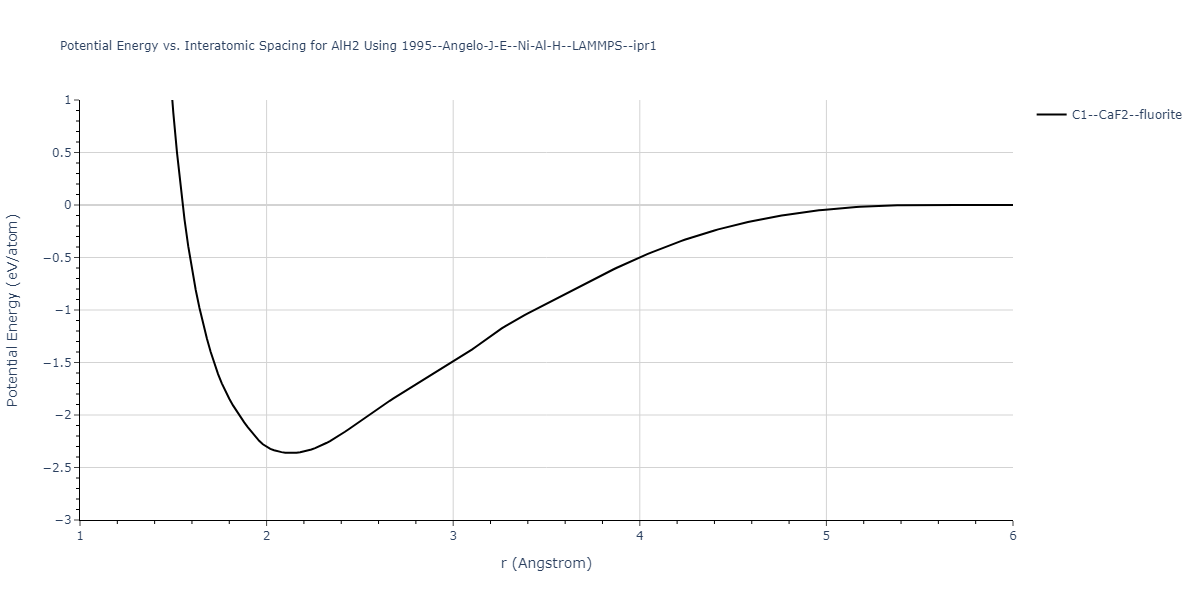
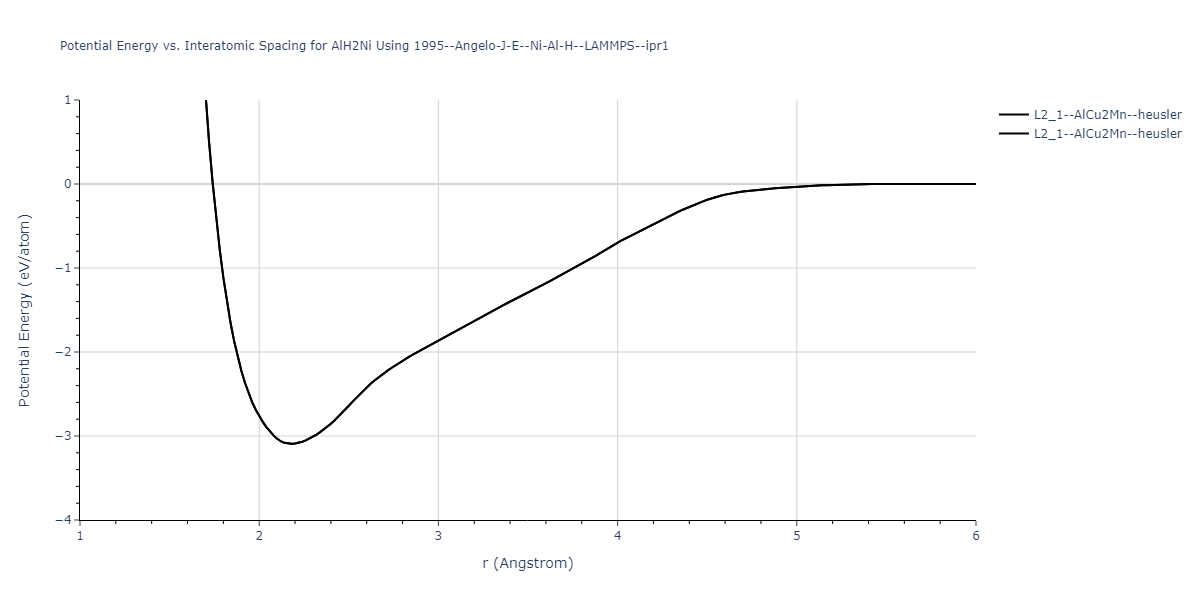
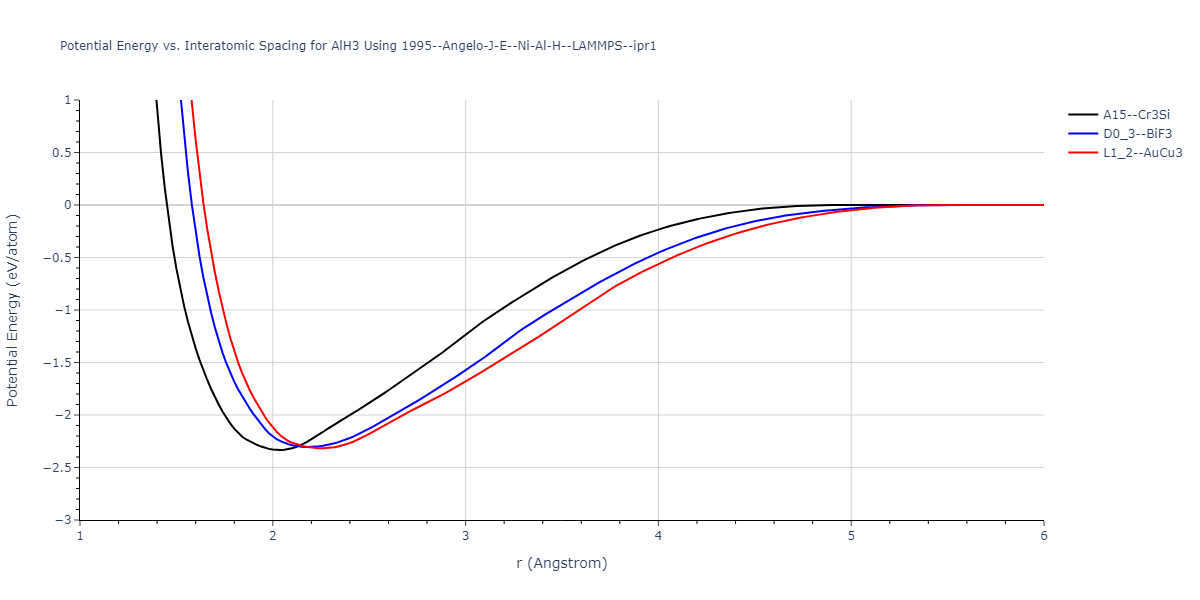
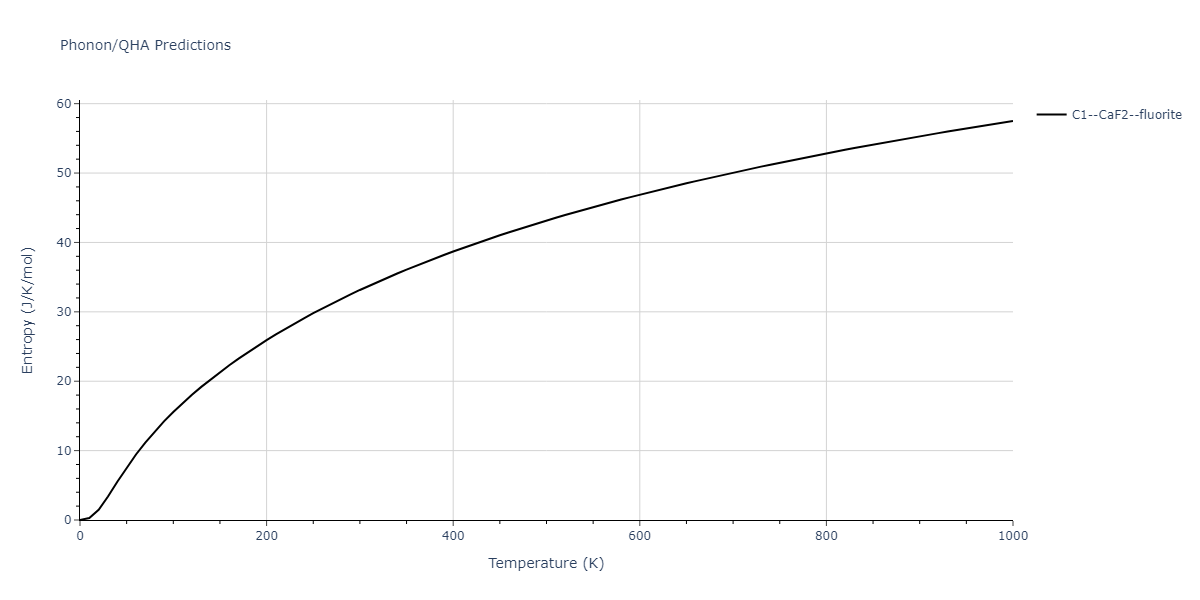
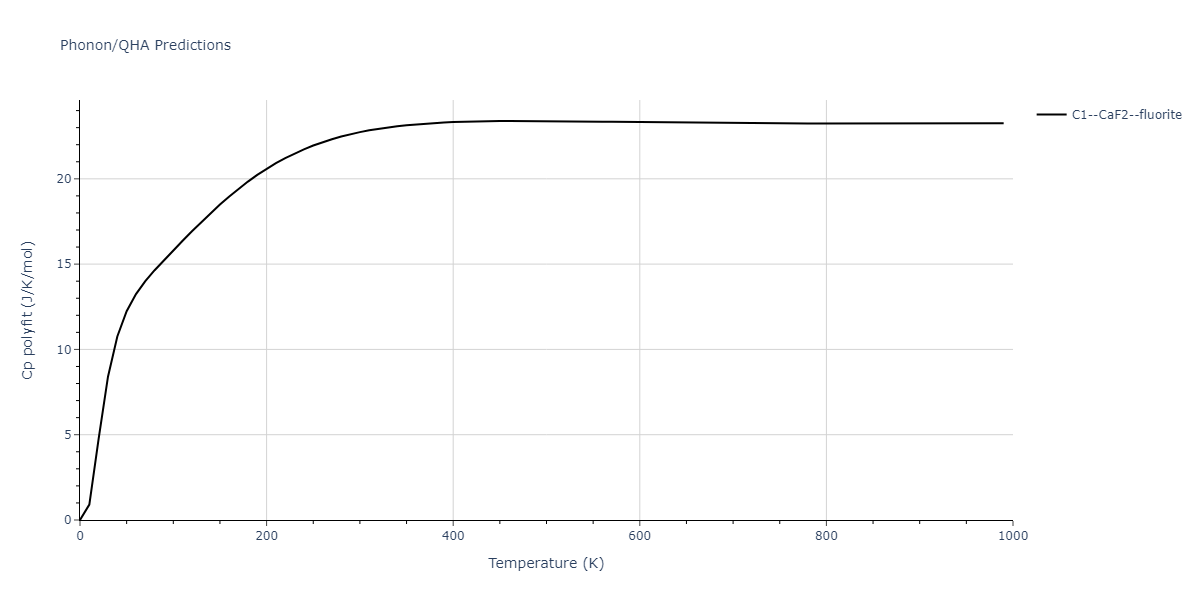
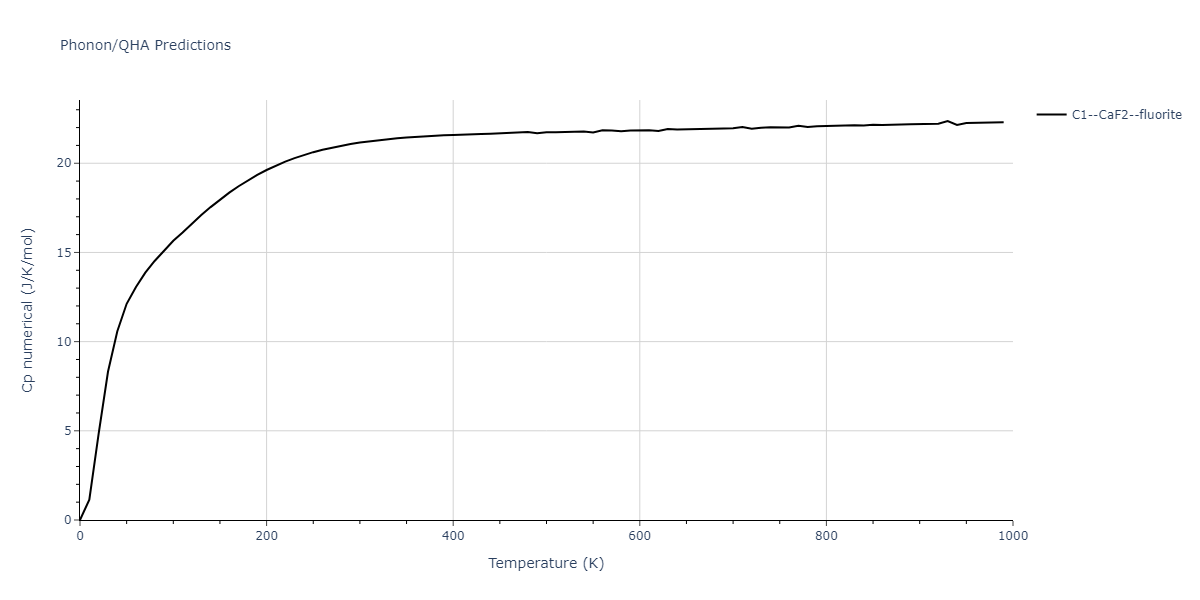
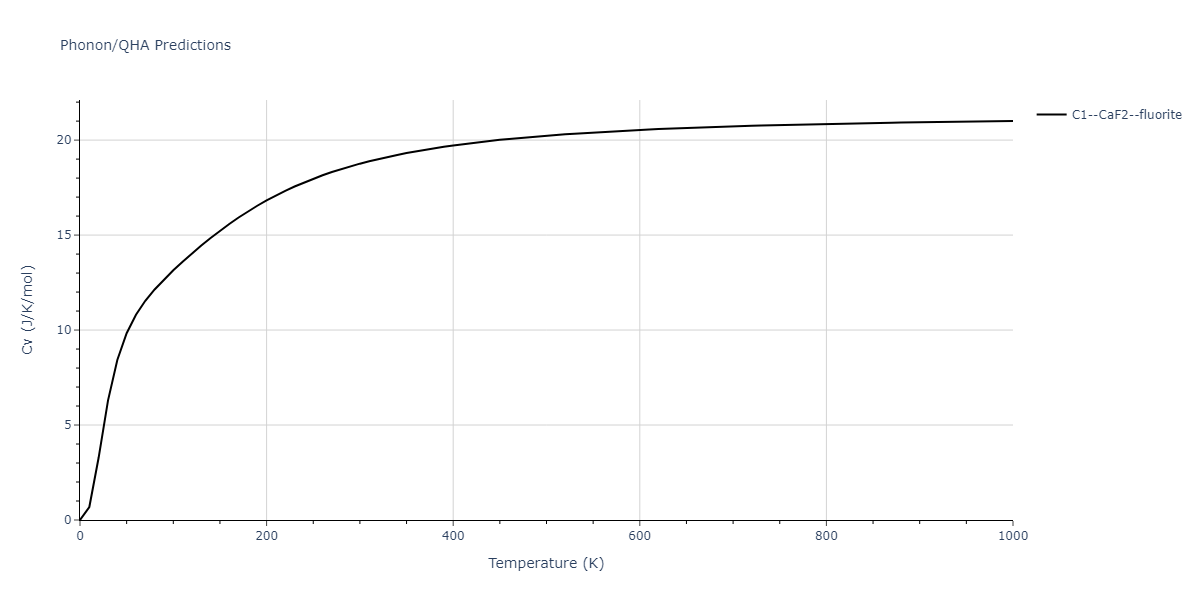
Diatom Energy vs. Interatomic Spacing
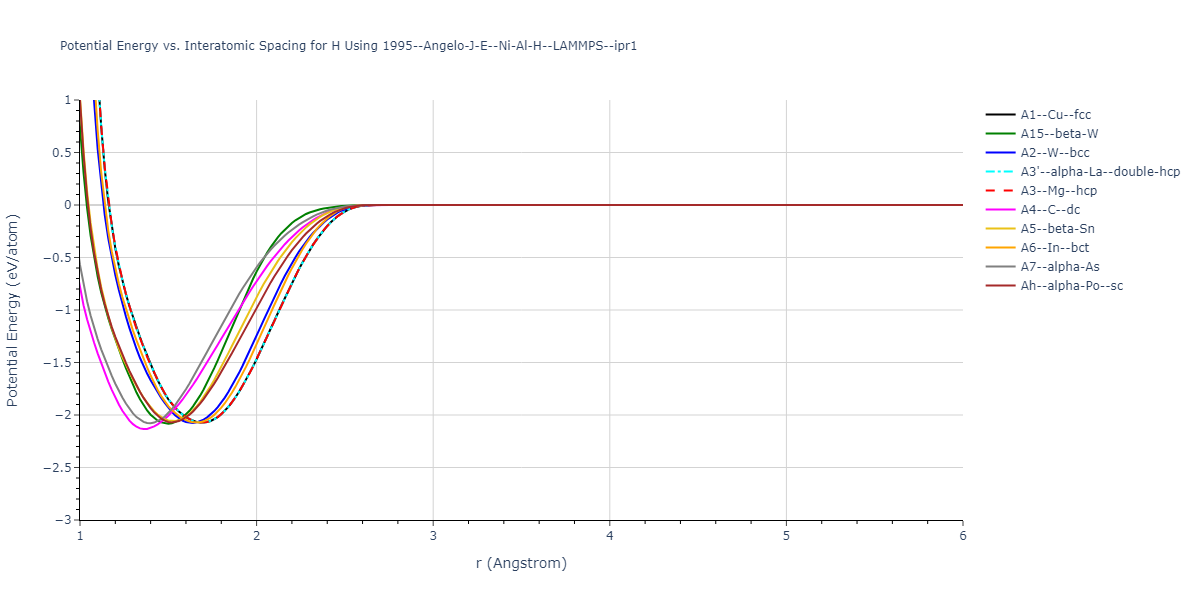
Plots of the potential energy vs interatomic spacing, r, are shown below for all diatom sets associated with the interatomic potential. This calculation provides insights into the functional form of the potential's two-body interactions. A system consisting of only two atoms is created, and the potential energy is evaluated for the atoms separated by 0.02 Å <= r <= 6.0> Å in intervals of 0.02 Å. Two plots are shown: one for the "standard" interaction distance range, and one for small values of r. The small r plot is useful for determining whether the potential is suitable for radiation studies.
The calculation method used is available as the iprPy diatom_scan calculation method.
Clicking on the image of a plot will open an interactive version of it in a new tab. The underlying data for the plots can be downloaded by clicking on the links above each plot.
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for variations in calculation methods, simulation software and implementations of the interatomic potentials.
- As this calculation only involves two atoms, it neglects any multi-body interactions that may be important in molecules, liquids and crystals.
- NIST disclaimer
Version Information:
- 2019-11-14. Maximum value range on the shortrange plots are now limited to "expected" levels as details are otherwise lost.
- 2019-08-07. Plots added.
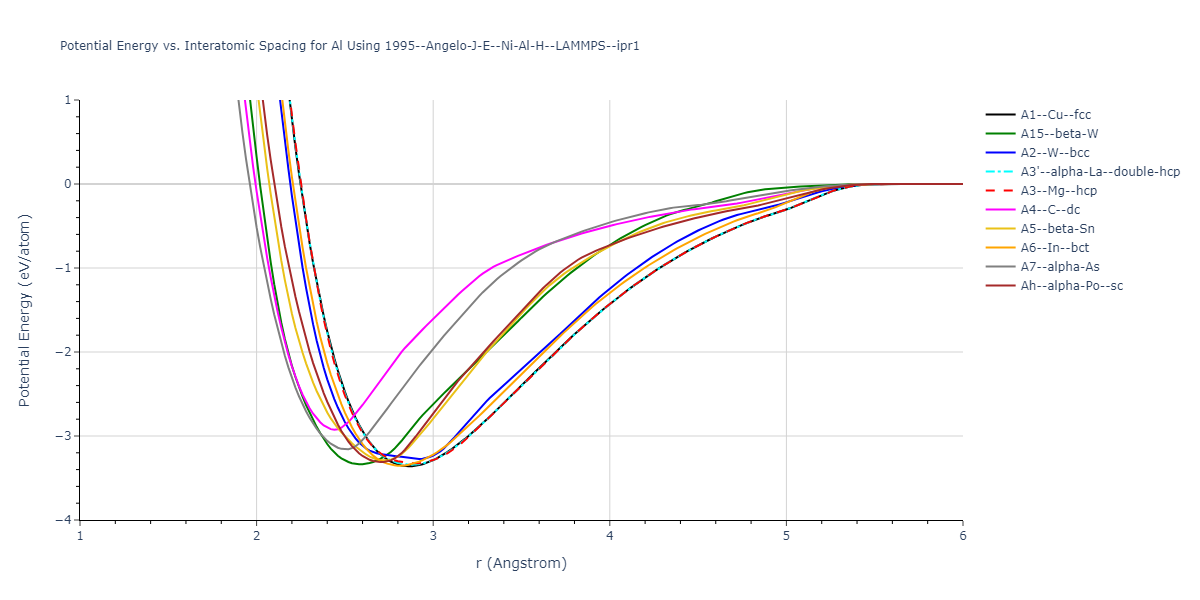
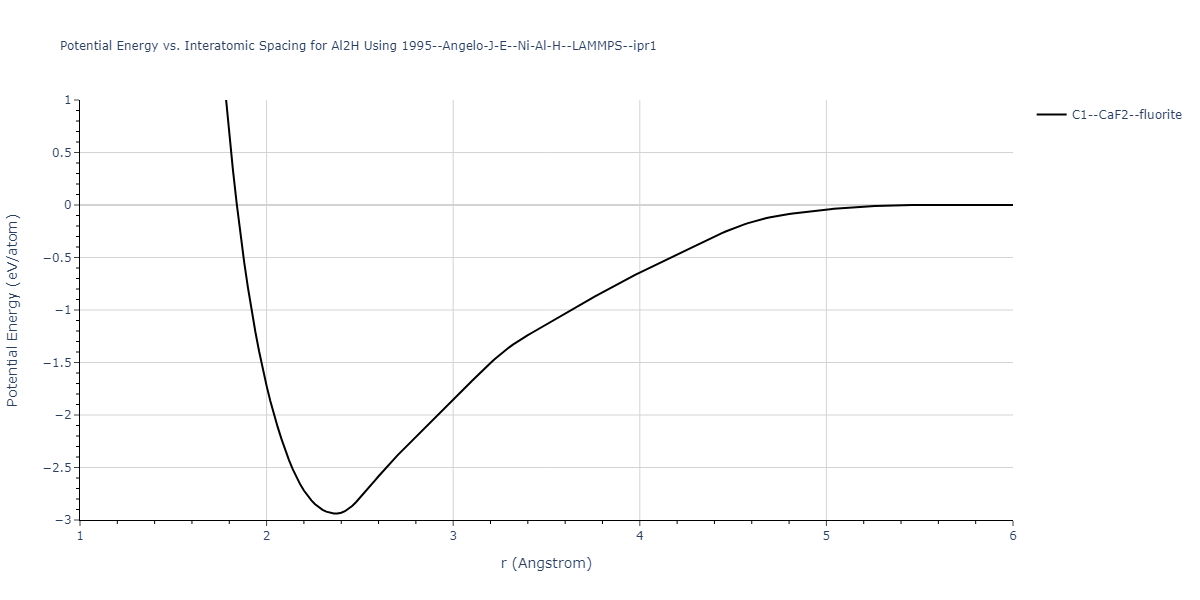
Cohesive Energy vs. Interatomic Spacing
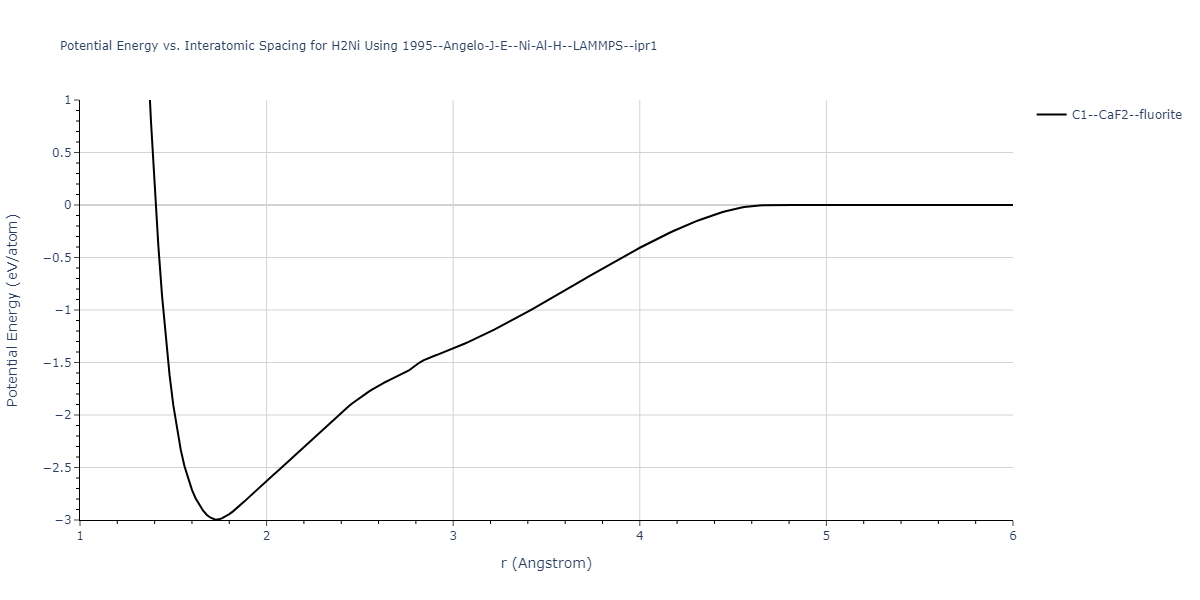
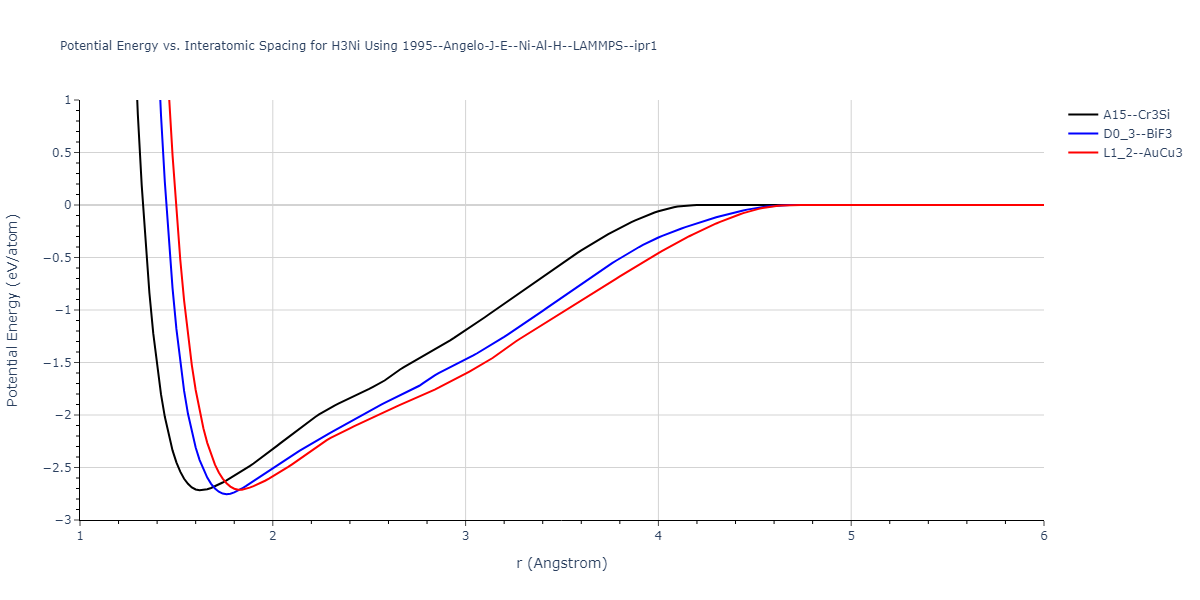
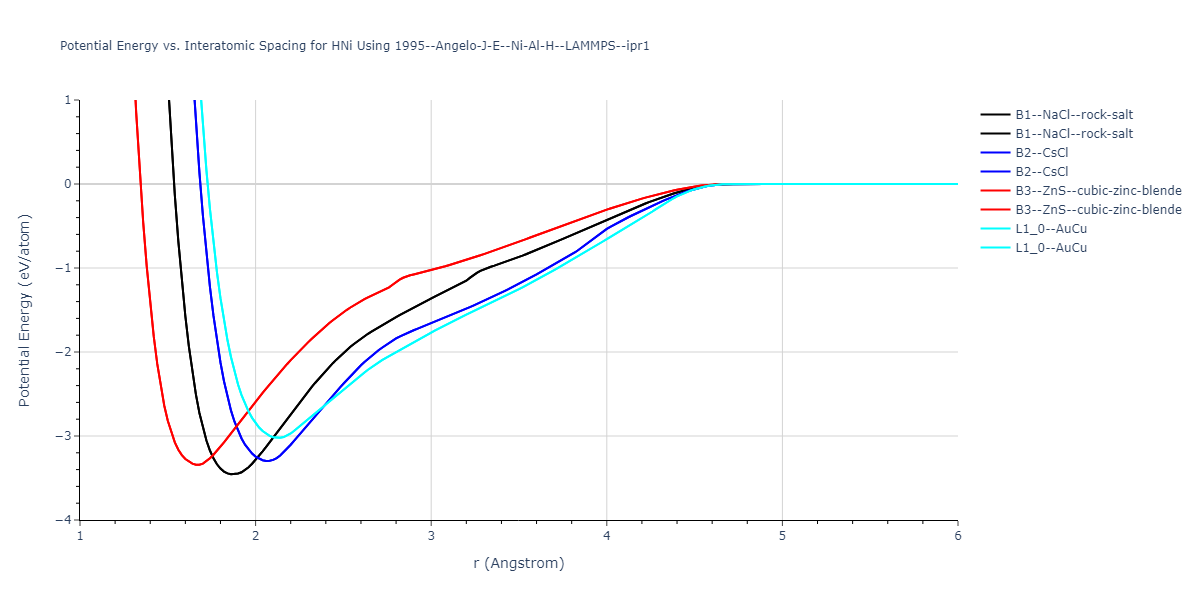
Plots of potential energy vs interatomic spacing, r, are shown below for a number of crystal structures. The structures are generated based on the ideal atomic positions and b/a and c/a lattice parameter ratios for a given crystal prototype. The size of the system is then uniformly scaled, and the energy calculated without relaxing the system. To obtain these plots, values of r are evaluated every 0.02 Å up to 6 Å.
The calculation method used is available as the iprPy E_vs_r_scan calculation method.
Clicking on the image of a plot will open an interactive version of it in a new tab. The underlying data for the plots can be downloaded by clicking on the links above each plot.
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for variations in calculation methods, simulation software and implementations of the interatomic potentials.
- The minima identified by this calculation do not guarantee that the associated crystal structures will be stable since no relaxation is performed.
- NIST disclaimer
Version Information:
- 2020-12-18. Descriptions, tables and plots updated to reflect that the energy values are the measuredper atom potential energy rather than cohesive energy as some potentials have non-zero isolated atom energies.
- 2019-02-04. Values regenerated with even r spacings of 0.02 Å, and now include values less than 2 Å when possible. Updated calculation method and parameters enhance compatibility with more potential styles.
- 2019-04-26. Results for hcp, double hcp, α-As and L10 prototypes regenerated from different unit cell representations. Only α-As results show noticable (>1e-5 eV) difference due to using a different coordinate for Wykoff site c position.
- 2018-06-13. Values for MEAM potentials corrected. Dynamic versions of the plots moved to separate pages to improve page loading. Cosmetic changes to how data is shown and updates to the documentation.
- 2017-01-11. Replaced png pictures with interactive Bokeh plots. Data regenerated with 200 values of r instead of 300.
- 2016-09-28. Plots for binary structures added. Data and plots for elemental structures regenerated. Data values match the values of the previous version. Data table formatting slightly changed to increase precision and ensure spaces between large values. Composition added to plot title and structure names made longer.
- 2016-04-07. Plots for elemental structures added.
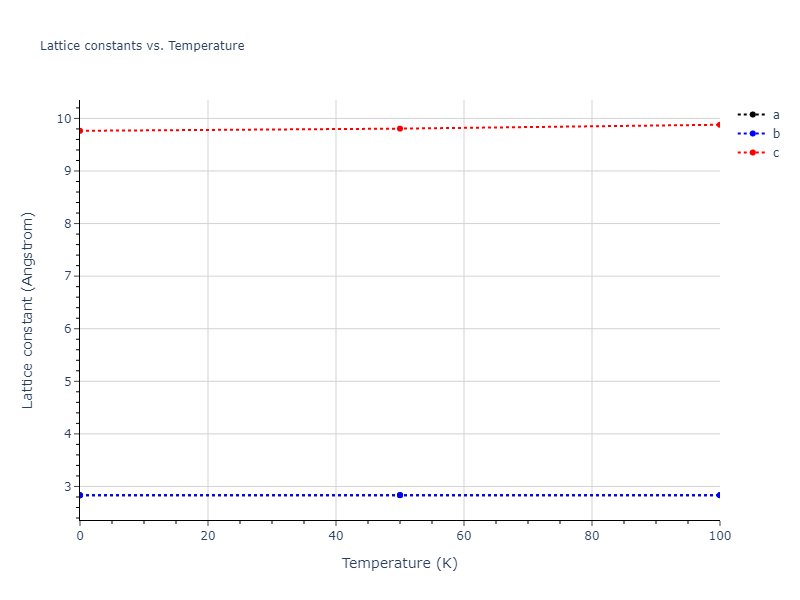
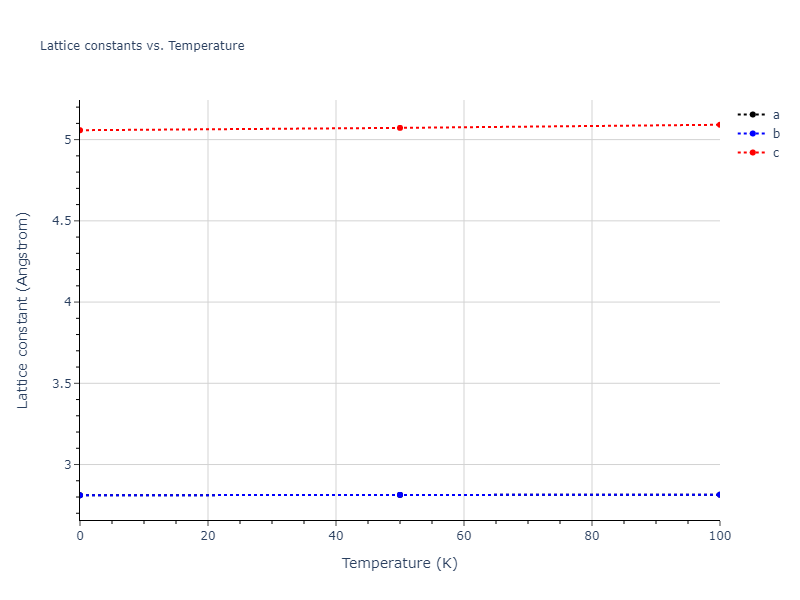
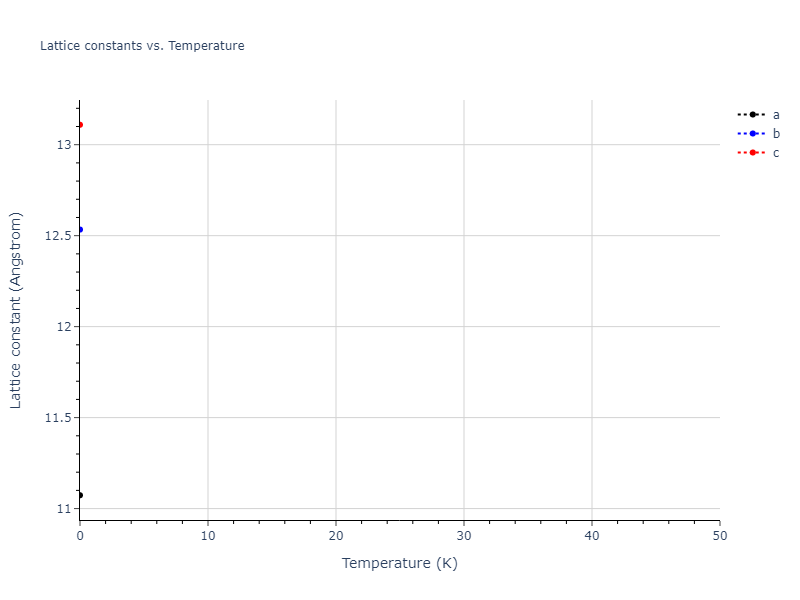
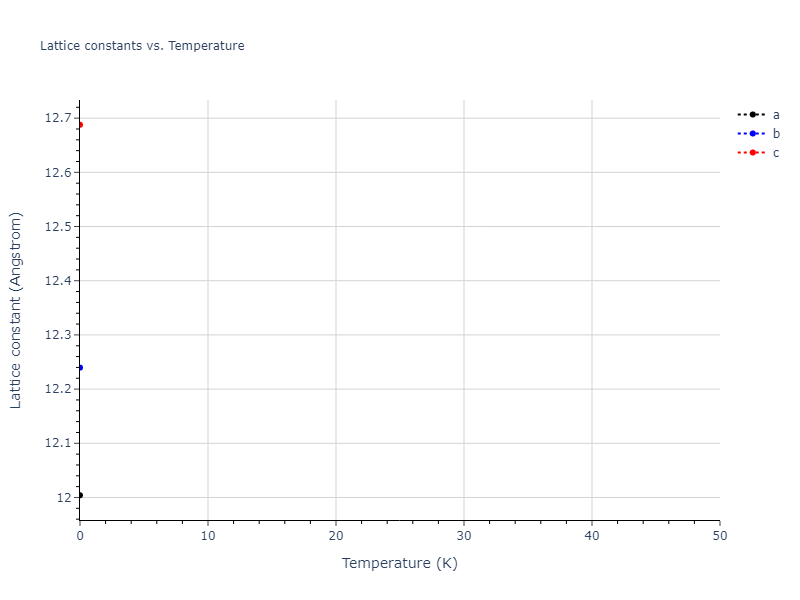
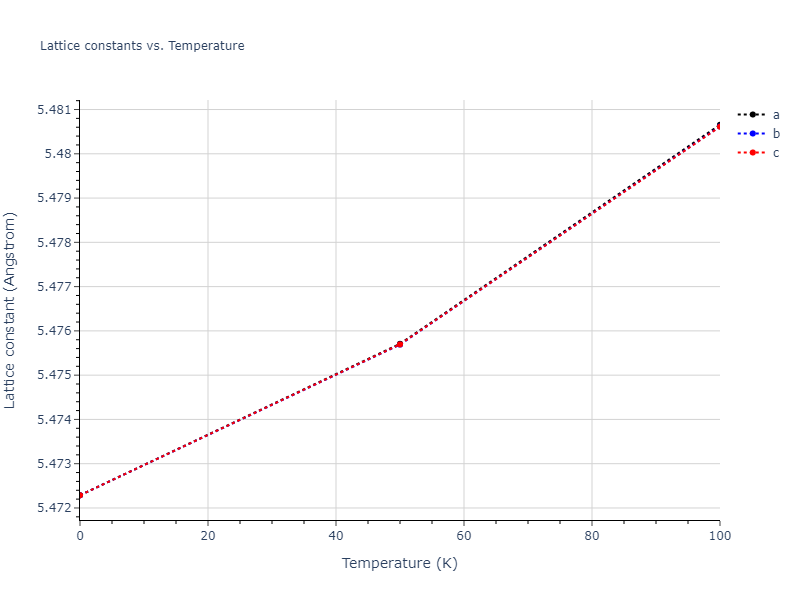
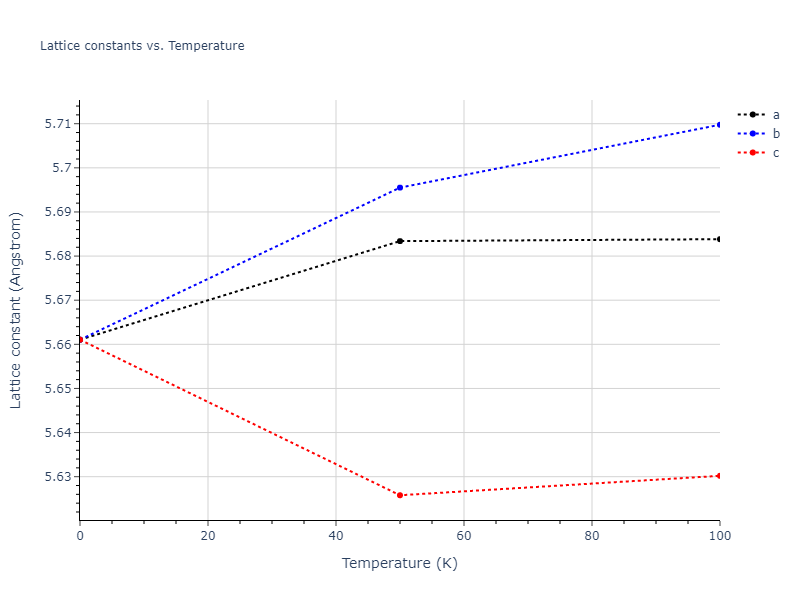
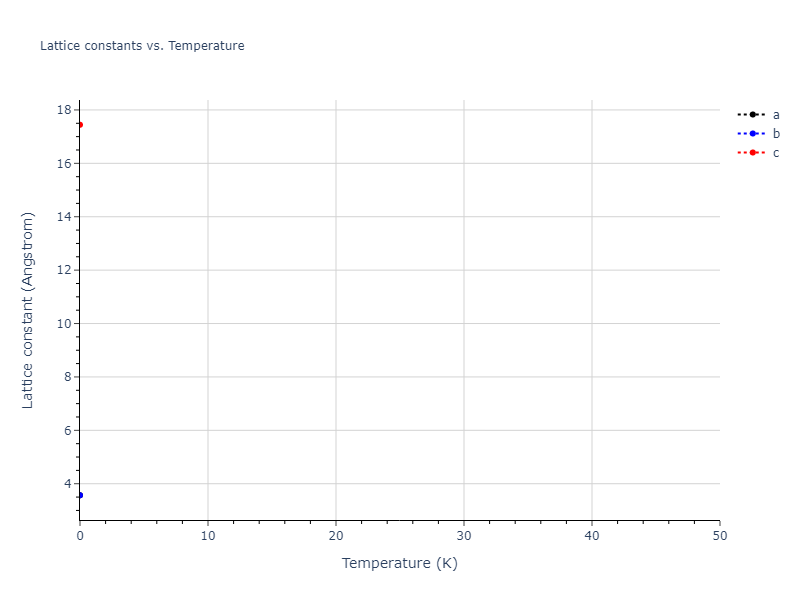
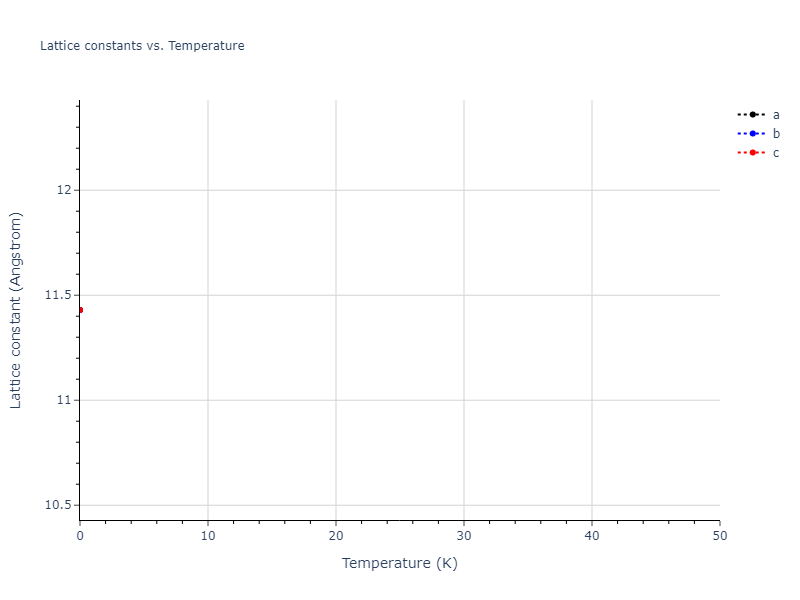
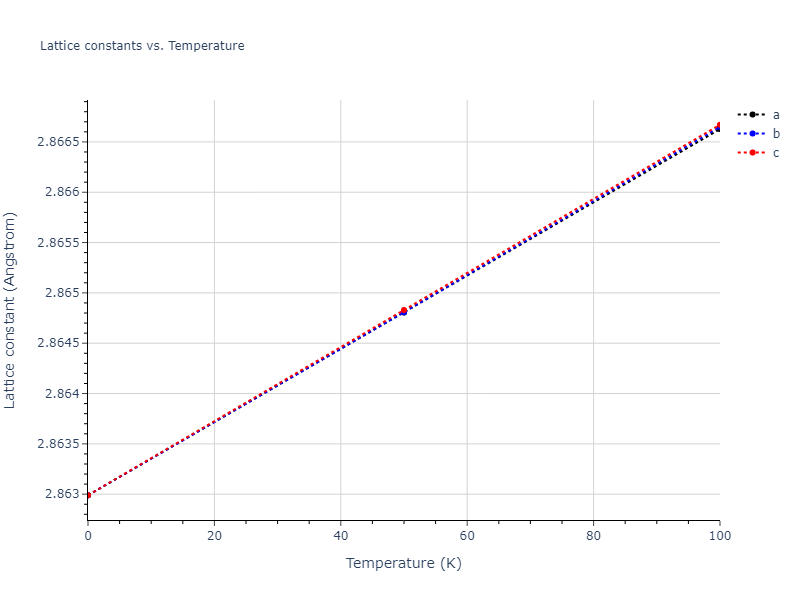
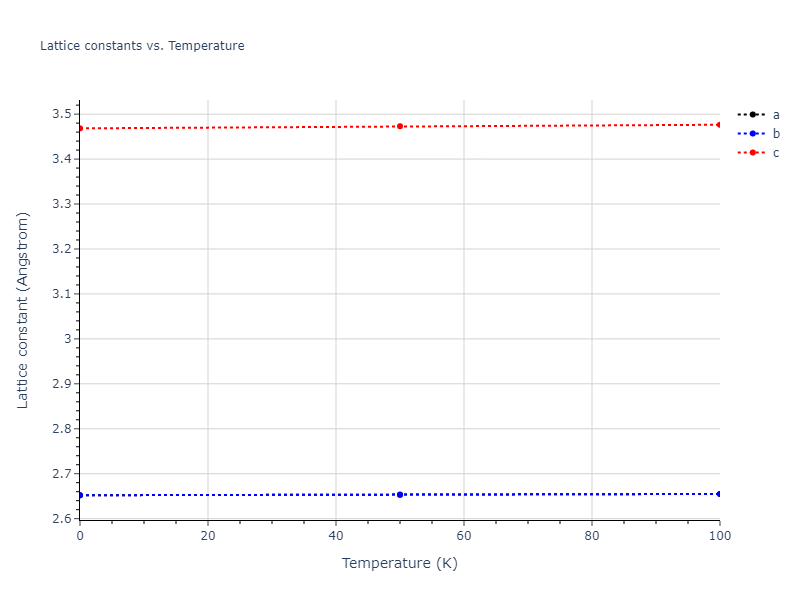
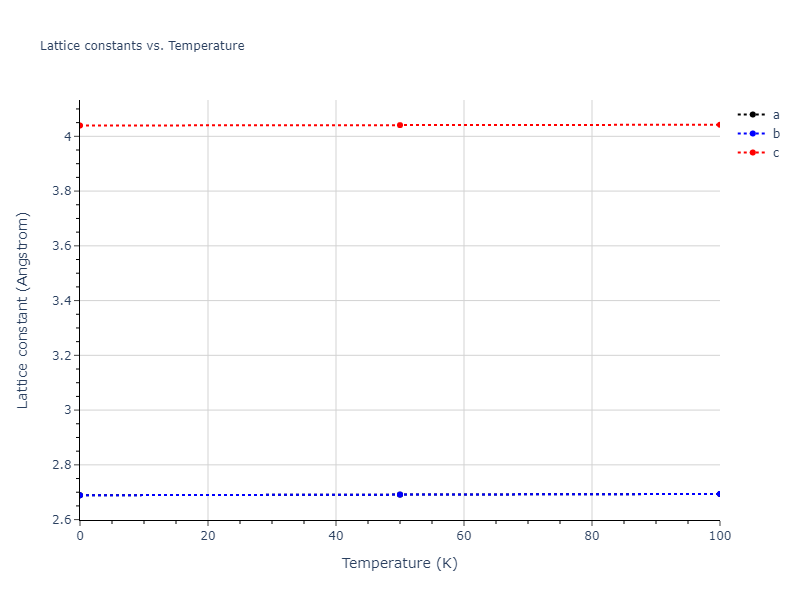
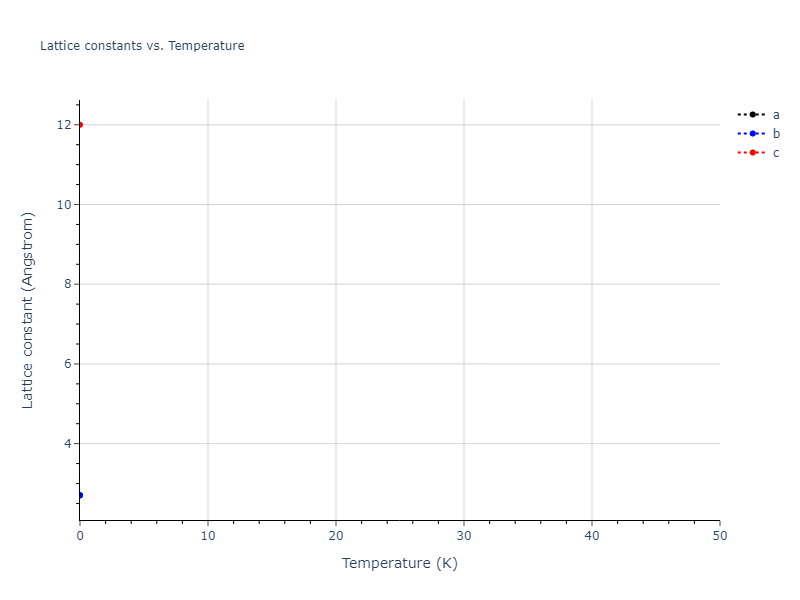
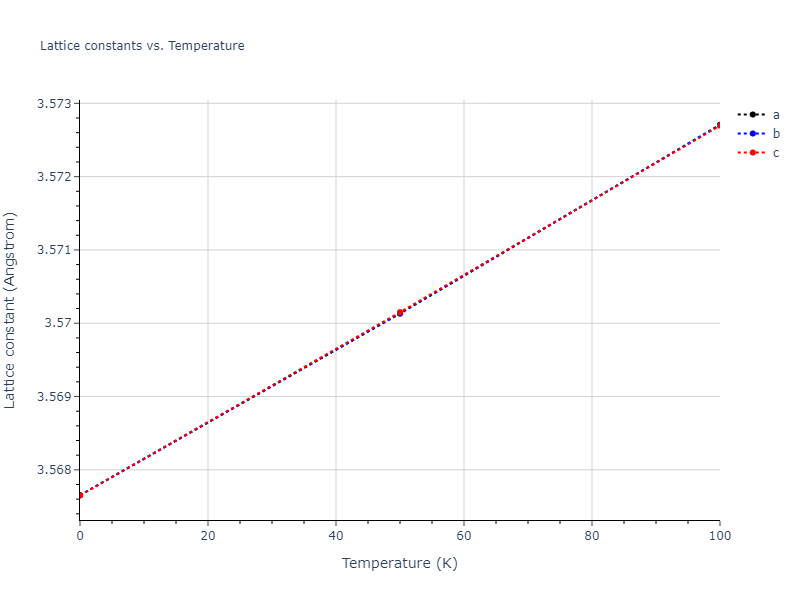
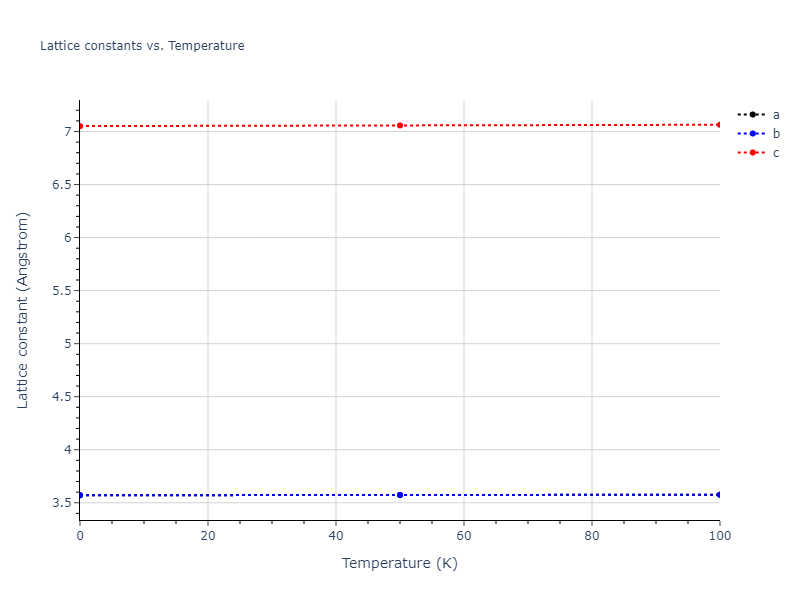
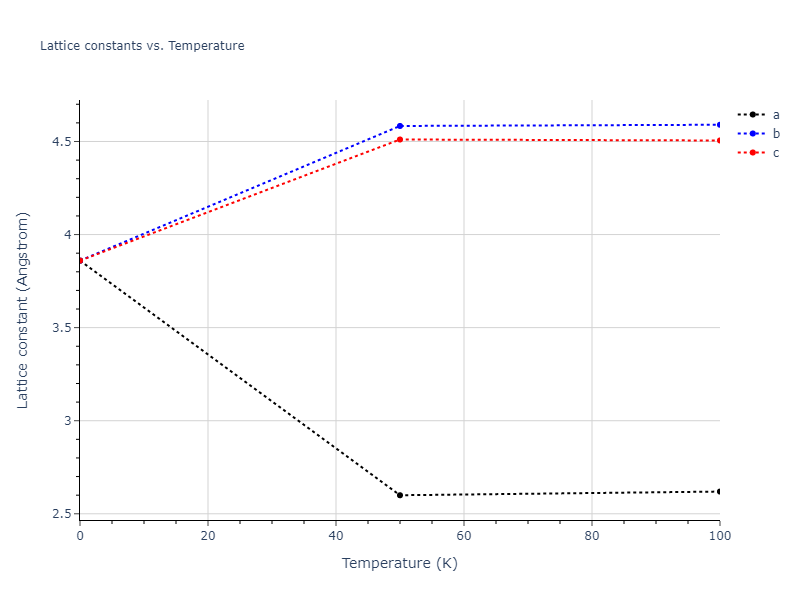
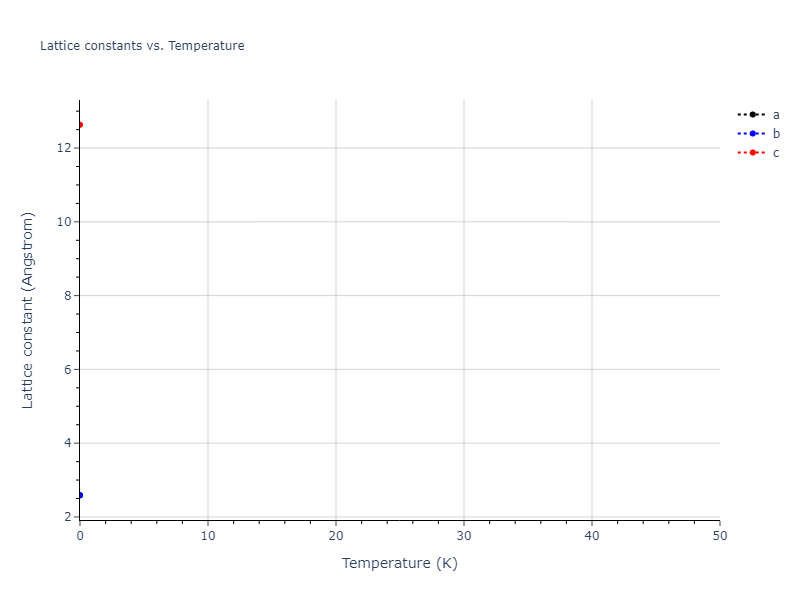
Crystal Structure Predictions
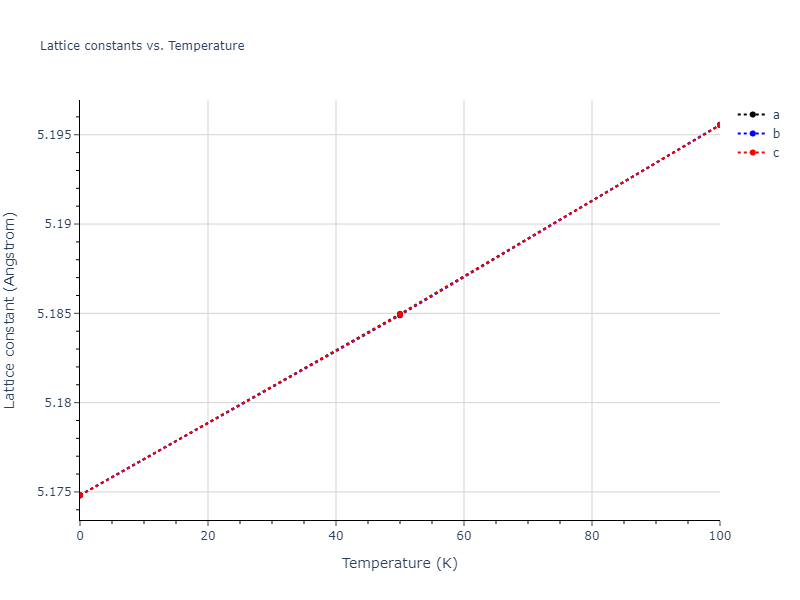
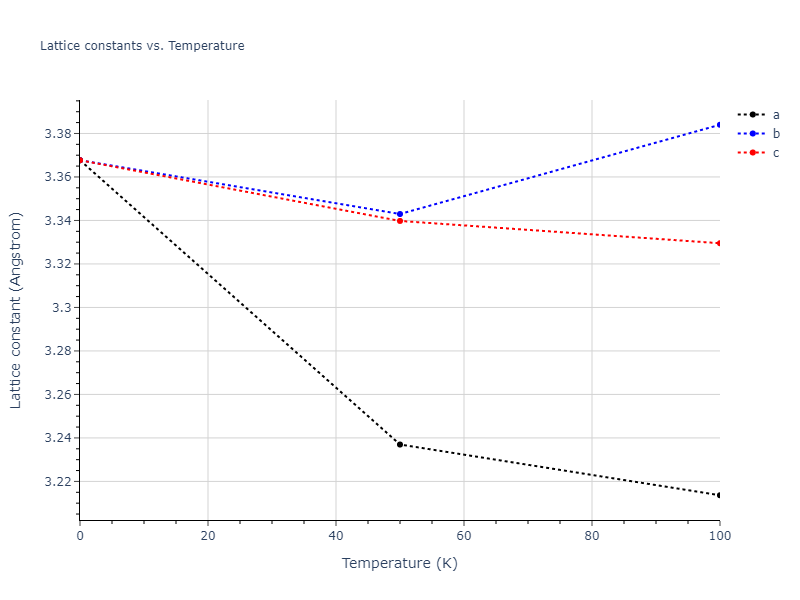
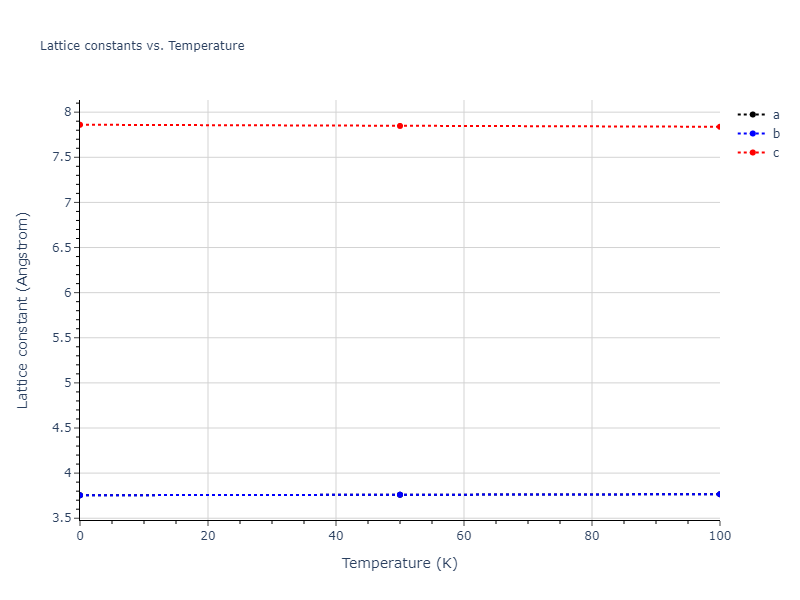
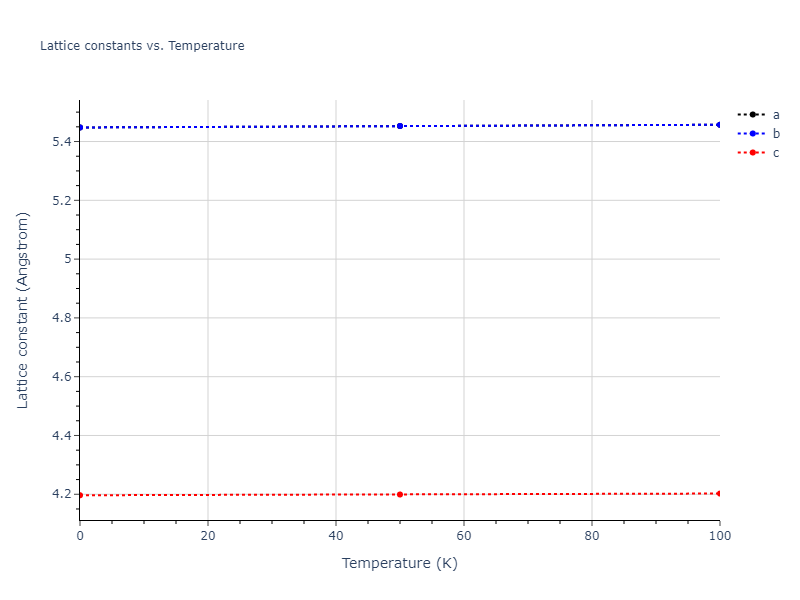
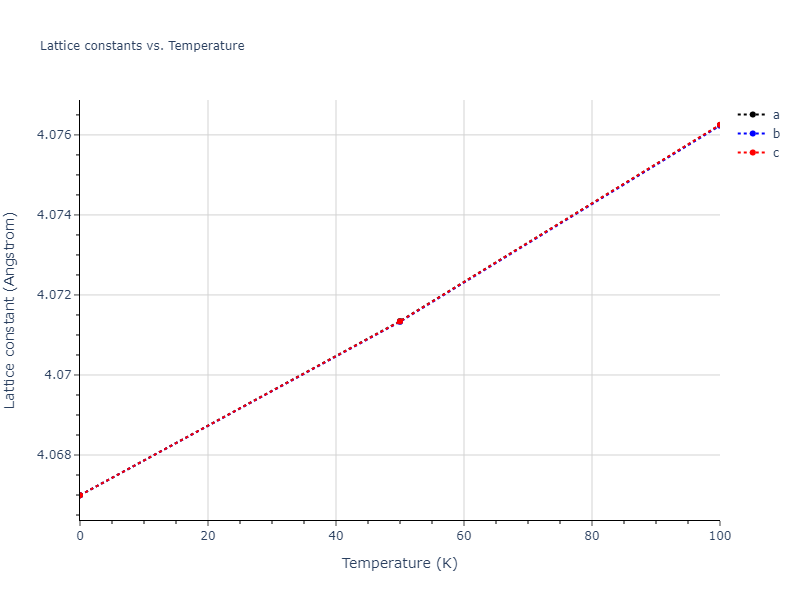
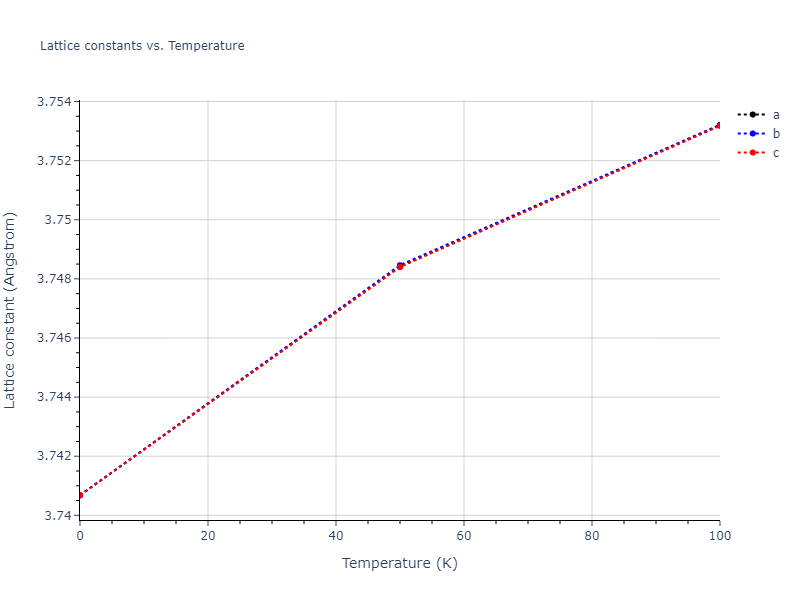
Computed lattice constants and cohesive/potential energies are displayed for a variety of crystal structures. The values displayed here are obtained using the following process.
- Initial crystal structure guesses are taken from:
- The iprPy E_vs_r_scan calculation results (shown above) by identifying all energy minima along the measured curves for a given crystal prototype + composition.
- Structures in the Materials Project and OQMD DFT databases.
- All initial guesses are relaxed using three independent methods using a 10x10x10 supercell:
- "box": The system's lattice constants are adjusted to zero pressure without internal relaxations using the iprPy relax_box calculation with a strainrange of 1e-6.
- "static": The system's lattice and atomic positions are statically relaxed using the iprPy relax_static calculation with a minimization force tolerance of 1e-10 eV/Angstrom.
- "dynamic": The system's lattice and atomic positions are dynamically relaxed for 10000 timesteps of 0.01 ps using the iprPy relax_dynamic calculation with an nph integration plus Langevin thermostat. The final configuration is then used as input in running an iprPy relax_static calculation with a minimization force tolerance of 1e-10 eV/Angstrom.
- The relaxed structures obtained from #2 are then evaluated using the spglib package to identify an ideal crystal unit cell based on the results.
- The space group information of the ideal unit cells is compared to the space group information of the corresponding reference structures to identify which structures transformed upon relaxation. The structures that did not transform to a different structure are listed in the table(s) below. The "method" field indicates the most rigorous relaxation method where the structure did not transform. The space group information is also used to match the DFT reference structures to the used prototype, where possible.
- The cohesive energy, Ecoh, is calculated from the measured potential energy per atom, Epot$, by subtracting the isolated energy averaged across all atoms in the unit cell. The isolated atom energies of each species model is obtained either by evaluating a single atom atomic configuration, or by identifying the first energy plateau from the diatom scan calculations for r > 2 Å.
The calculation methods used are implemented into iprPy as the following calculation styles
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for variations in calculation methods, simulation software and implementations of the interatomic potentials.
- The presence of any structures in this list does not guarantee that those structures are stable. Also, the lowest energy structure may not be included in this list.
- Multiple values for the same crystal structure but different lattice constants are possible. This is because multiple energy minima are possible for a given structure and interatomic potential. Having multiple energy minima for a structure does not necessarily make the potential "bad" as unwanted configurations may be unstable or correspond to conditions that may not be relevant to the problem of interest (eg. very high strains).
- NIST disclaimer
Version Information:
- 2025-07-02. All "mp-" reference structure calculations were re-relaxed using the updated Materials Project database rather than the original database structures. Also, a bug was fixed that caused the "static" relaxations to occasionally throw unnecessary errors. This was fixed and all affected calculations were reset and performed again.
- 2022-05-27. The "box" method results have all been redone with an updated methodology more suited for non-orthogonal systems.
- 2020-12-18. Cohesive energies have been corrected by making them relative to the energies of the isolated atoms. The previous cohesive energy values are now listed as the potential energies.
- 2019-06-07. Structures with positive or near zero cohesive energies removed from the display tables. All values still present in the raw data files.
- 2019-04-26. Calculations now computed for each implementation. Results for hcp, double hcp, α-As and L10 prototypes regenerated from different unit cell representations.
- 2018-06-14. Methodology completely changed affecting how the information is displayed. Calculations involving MEAM potentials corrected.
- 2016-09-28. Values for simple compounds added. All identified energy minima for each structure are listed. The existing elemental data was regenerated. Most values are consistent with before, but some differences have been noted. Specifically, variations are seen with some values for potentials where the elastic constants don't vary smoothly near the equilibrium state. Additionally, the inclusion of some high-energy structures has changed based on new criteria for identifying when structures have relaxed to another structure.
- 2016-04-07. Values for elemental crystal structures added. Only values for the global energy minimum of each unique structure given.
Download raw data (including filtered results)
Reference structure matches:
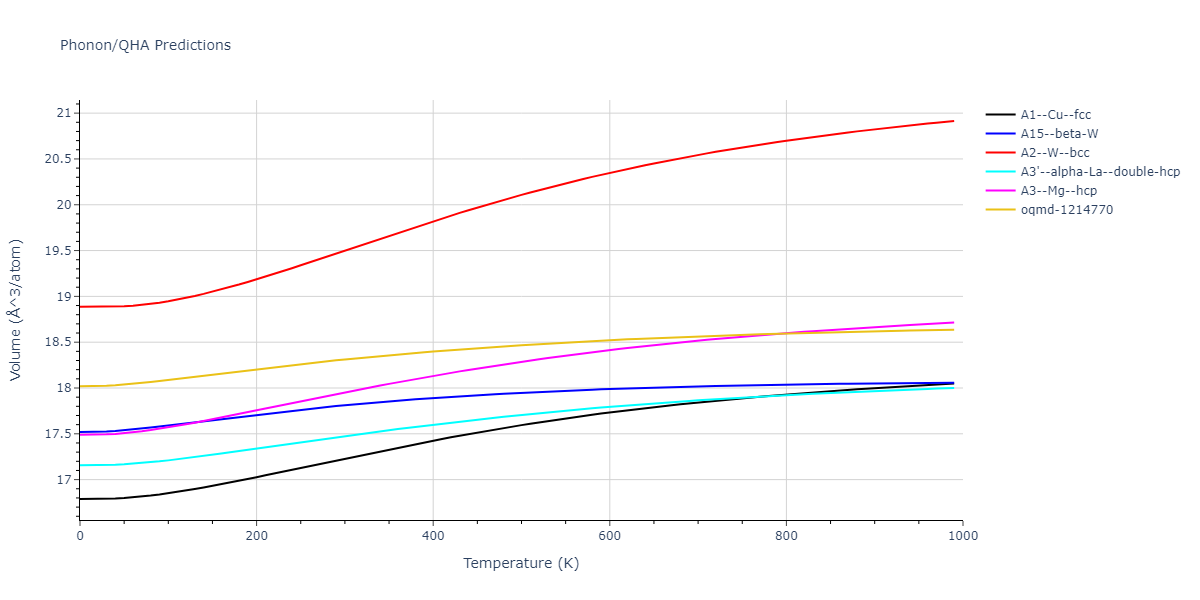
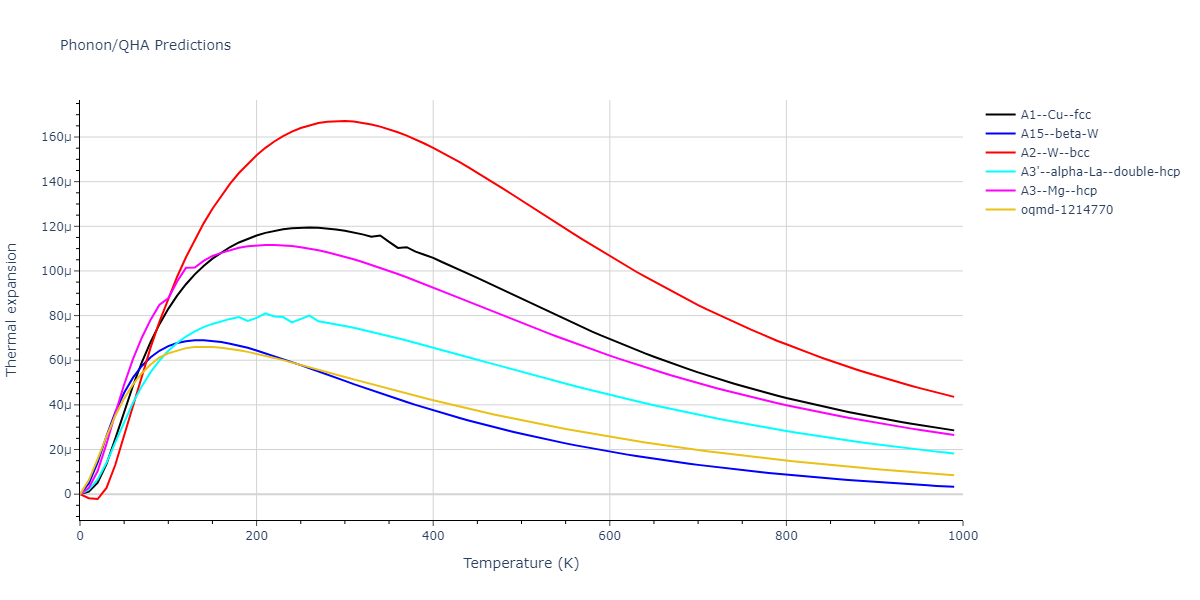
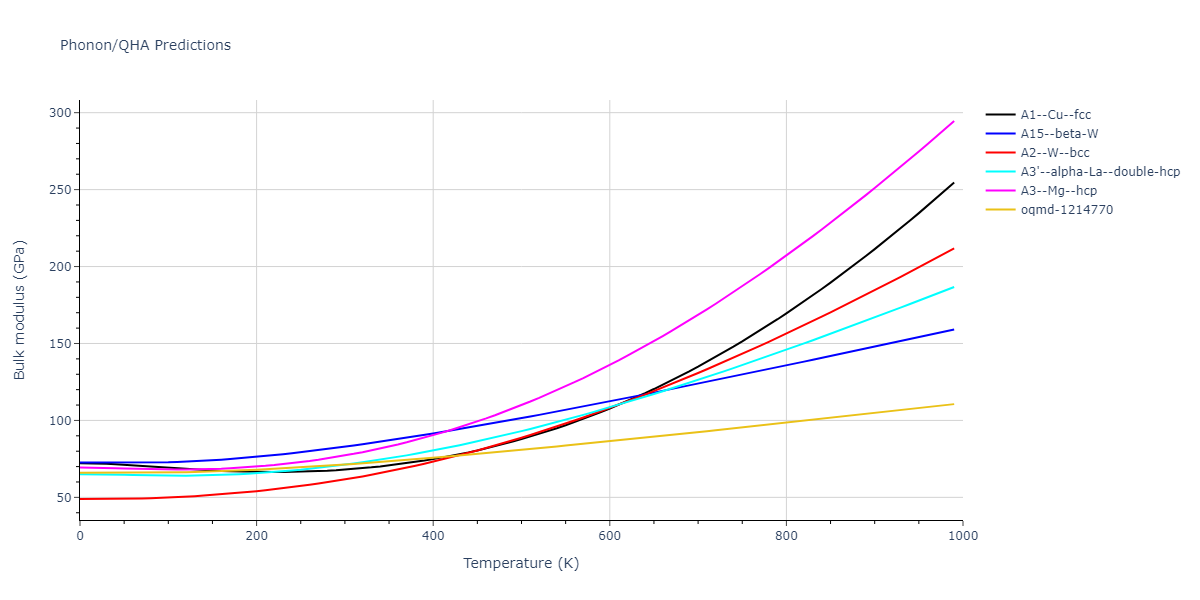
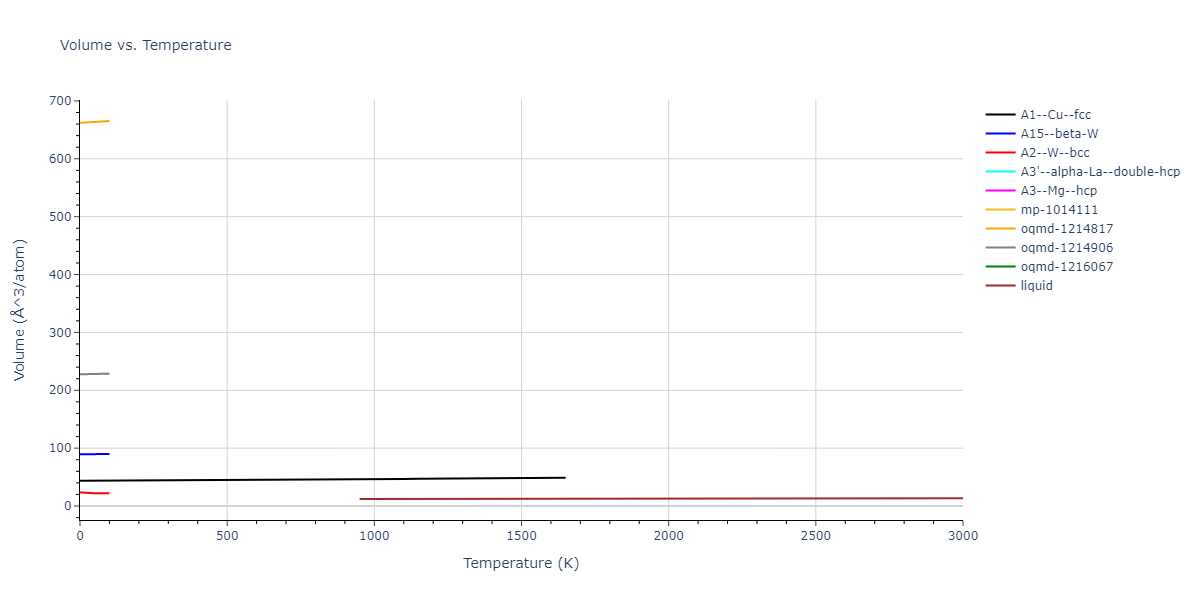
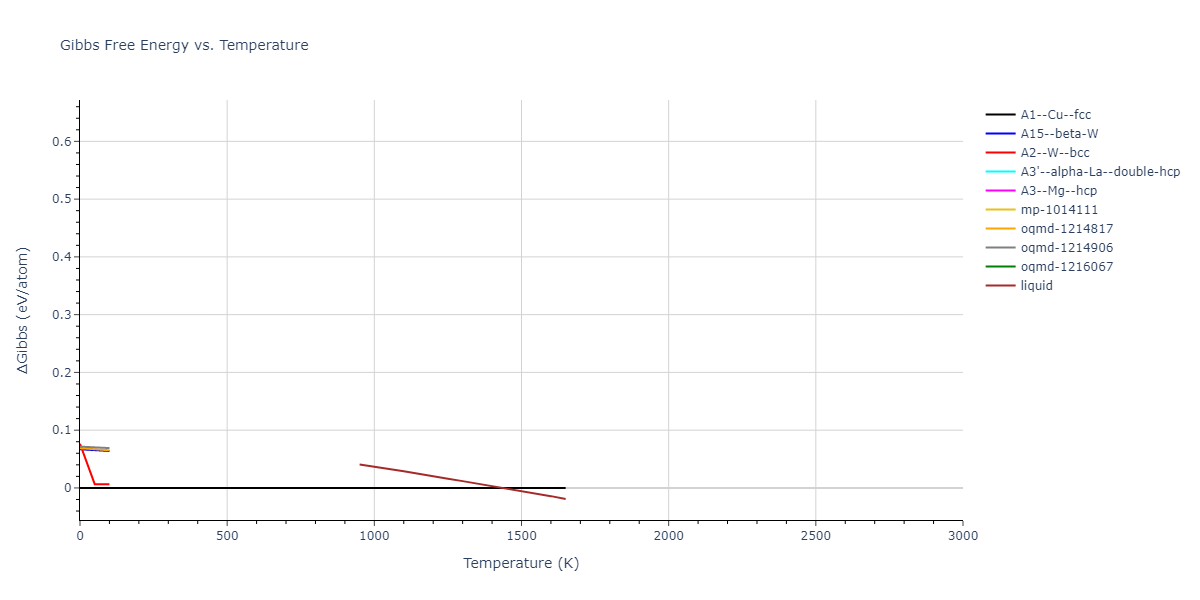
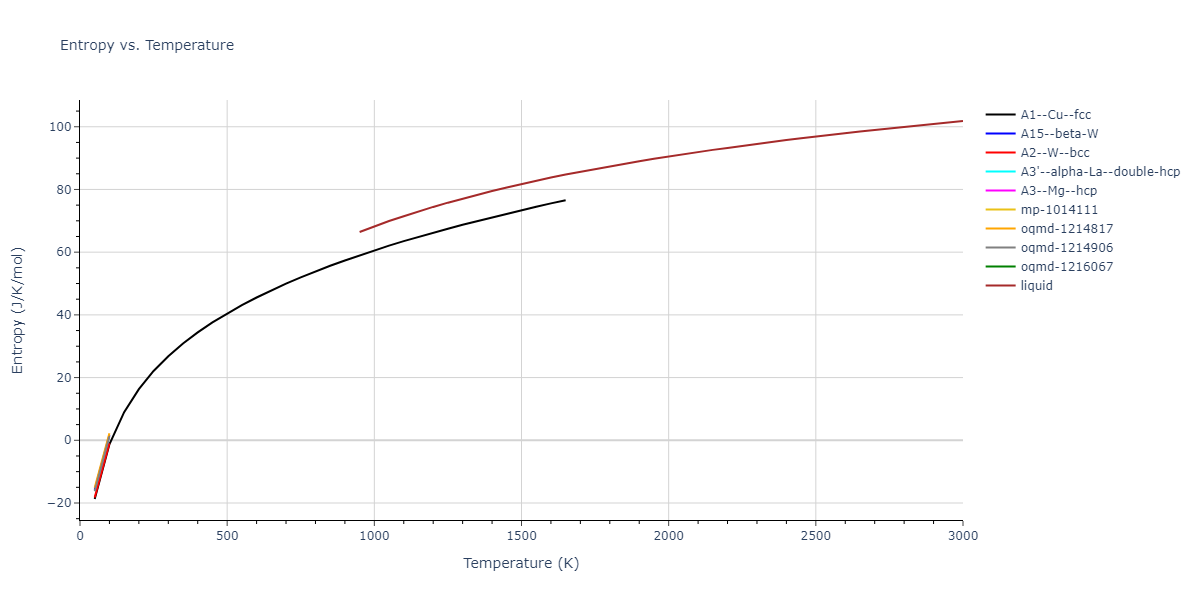
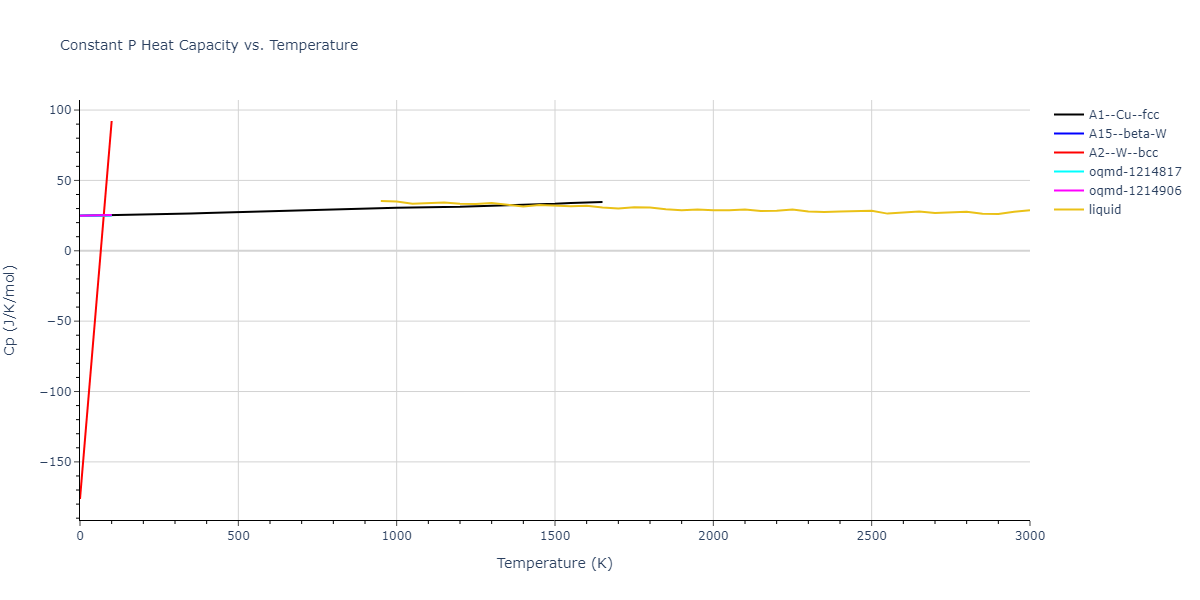
A1--Cu--fcc = mp-134, oqmd-8100, oqmd-1214503
A15--beta-W = oqmd-1214948, oqmd-1280406
A2--W--bcc = mp-998860, oqmd-1215126
A3'--alpha-La--double-hcp = mp-1183144, oqmd-1215394
A3--Mg--hcp = oqmd-1215215, oqmd-1215304
A4--C--dc = oqmd-1215483
A5--beta-Sn = oqmd-1215572
A6--In--bct = oqmd-1215661
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| A1--Cu--fcc | dynamic | -3.36 | -3.36 | 4.05 | 4.05 | 4.05 | 90.0 | 90.0 | 90.0 |
| A3--Mg--hcp | dynamic | -3.348 | -3.348 | 2.8109 | 2.8109 | 5.0579 | 90.0 | 90.0 | 120.0 |
| oqmd-1216017 | dynamic | -3.3479 | -3.3479 | 2.8256 | 2.8256 | 22.2291 | 90.0 | 90.0 | 120.0 |
| A3'--alpha-La--double-hcp | dynamic | -3.3478 | -3.3478 | 2.8327 | 2.8327 | 9.7644 | 90.0 | 90.0 | 120.0 |
| oqmd-1215037 | dynamic | -3.337 | -3.337 | 2.7611 | 5.006 | 10.989 | 90.0 | 90.0 | 90.0 |
| A15--beta-W | dynamic | -3.3363 | -3.3363 | 5.1748 | 5.1748 | 5.1748 | 90.0 | 90.0 | 90.0 |
| oqmd-1214770 | dynamic | -3.3338 | -3.3338 | 10.1051 | 10.1051 | 10.1051 | 90.0 | 90.0 | 90.0 |
| oqmd-1214770 | box | -3.3311 | -3.3311 | 10.0858 | 10.0858 | 10.0858 | 90.0 | 90.0 | 90.0 |
| oqmd-1214859 | static | -3.3251 | -3.3251 | 7.0398 | 7.0398 | 7.0398 | 90.0 | 90.0 | 90.0 |
| mp-1245307 | dynamic | -3.3228 | -3.3228 | 11.7994 | 12.1192 | 12.792 | 88.3 | 87.8 | 84.6 |
| mp-1245067 | dynamic | -3.3208 | -3.3208 | 12.0041 | 12.2396 | 12.6878 | 94.8 | 98.7 | 93.8 |
| mp-1245129 | dynamic | -3.3205 | -3.3205 | 11.5792 | 12.4682 | 12.6517 | 88.7 | 84.9 | 87.9 |
| mp-1244953 | dynamic | -3.3203 | -3.3203 | 11.0733 | 12.5337 | 13.1097 | 91.9 | 93.4 | 91.9 |
| mp-1245152 | dynamic | -3.3196 | -3.3196 | 11.8545 | 11.9806 | 12.9734 | 94.6 | 90.6 | 95.5 |
| mp-1244953 | static | -3.3163 | -3.3163 | 11.7609 | 12.3631 | 12.5549 | 88.3 | 85.5 | 87.7 |
| mp-1245067 | static | -3.3162 | -3.3162 | 12.0893 | 12.3105 | 12.3968 | 92.9 | 97.3 | 91.9 |
| mp-1245152 | static | -3.3154 | -3.3154 | 11.9069 | 12.044 | 12.861 | 90.5 | 93.2 | 98.2 |
| oqmd-1214859 | box | -3.3144 | -3.3144 | 7.0473 | 7.0473 | 7.0473 | 90.0 | 90.0 | 90.0 |
| Ah--alpha-Po--sc | static | -3.3111 | -3.3111 | 2.705 | 2.705 | 2.705 | 90.0 | 90.0 | 90.0 |
| mp-1245129 | box | -3.3055 | -3.3055 | 11.8347 | 12.2702 | 12.4776 | 93.5 | 92.6 | 95.4 |
| mp-1245152 | box | -3.3007 | -3.3007 | 12.0754 | 12.2451 | 12.3051 | 92.2 | 92.6 | 96.8 |
| mp-1244953 | box | -3.3 | -3.3 | 12.1672 | 12.2061 | 12.2915 | 87.1 | 81.2 | 87.1 |
| mp-1245067 | box | -3.2992 | -3.2992 | 12.0178 | 12.3476 | 12.38 | 92.7 | 94.0 | 97.1 |
| mp-1245307 | box | -3.2983 | -3.2983 | 11.997 | 12.2704 | 12.3069 | 91.0 | 93.3 | 93.4 |
| A5--beta-Sn | static | -3.2925 | -3.2925 | 5.2442 | 5.2442 | 2.8922 | 90.0 | 90.0 | 90.0 |
| A2--W--bcc | dynamic | -3.2734 | -3.2734 | 3.3677 | 3.3677 | 3.3677 | 90.0 | 90.0 | 90.0 |
| oqmd-1214681 | box | -3.2552 | -3.2552 | 4.2517 | 7.9963 | 4.5618 | 90.0 | 90.0 | 90.0 |
| oqmd-1215928 | box | -3.041 | -3.041 | 4.3509 | 4.3509 | 5.0887 | 90.0 | 90.0 | 120.0 |
| mp-1239196 | static | -2.961 | -2.961 | 3.6275 | 3.6275 | 12.8594 | 90.0 | 90.0 | 90.0 |
| mp-1239196 | box | -2.9308 | -2.9308 | 3.714 | 3.714 | 12.5691 | 90.0 | 90.0 | 90.0 |
| A4--C--dc | static | -2.9243 | -2.9243 | 5.636 | 5.636 | 5.636 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
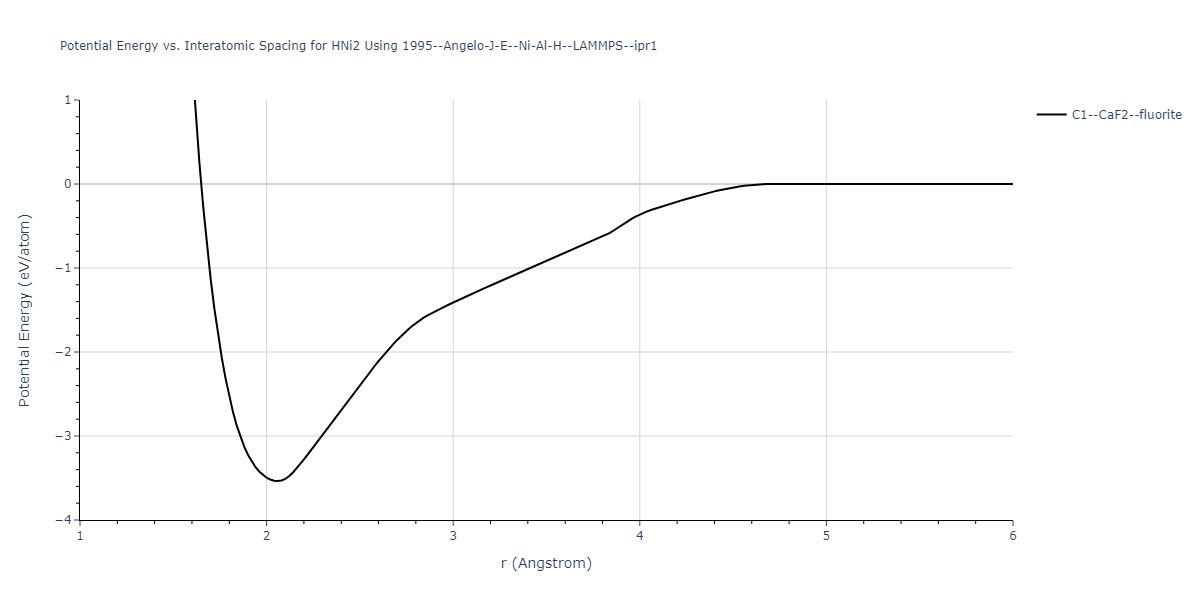
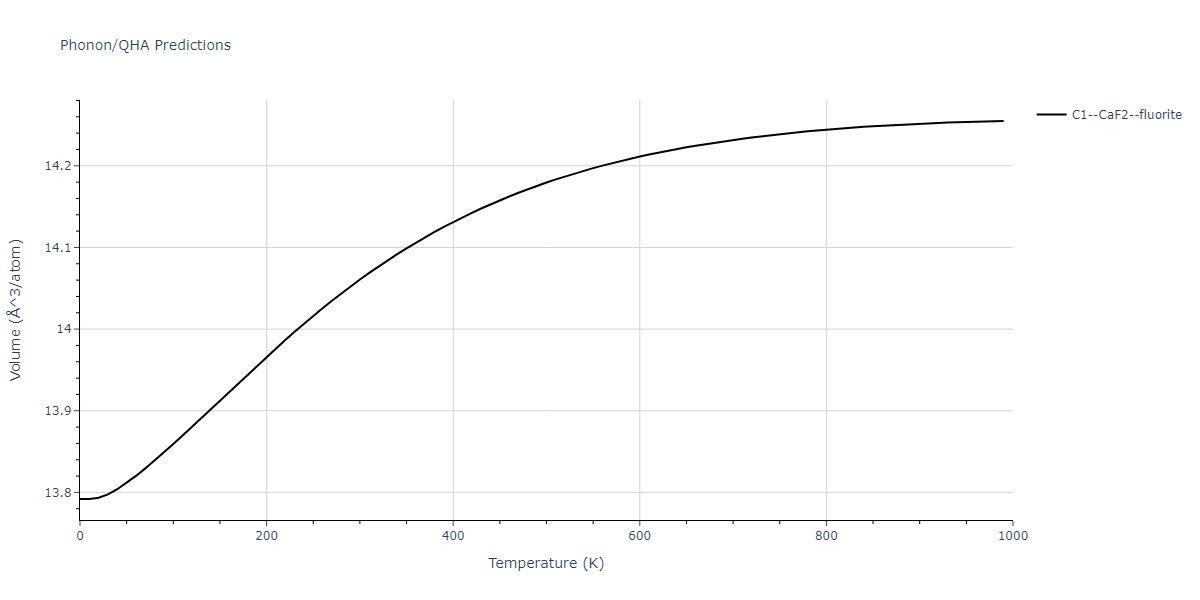
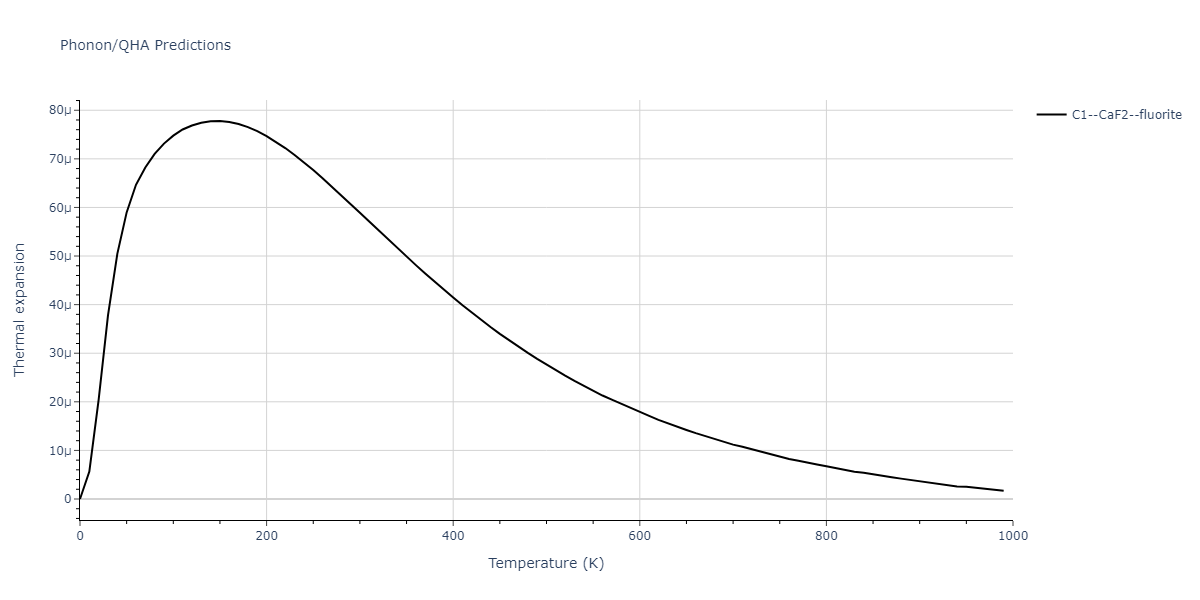
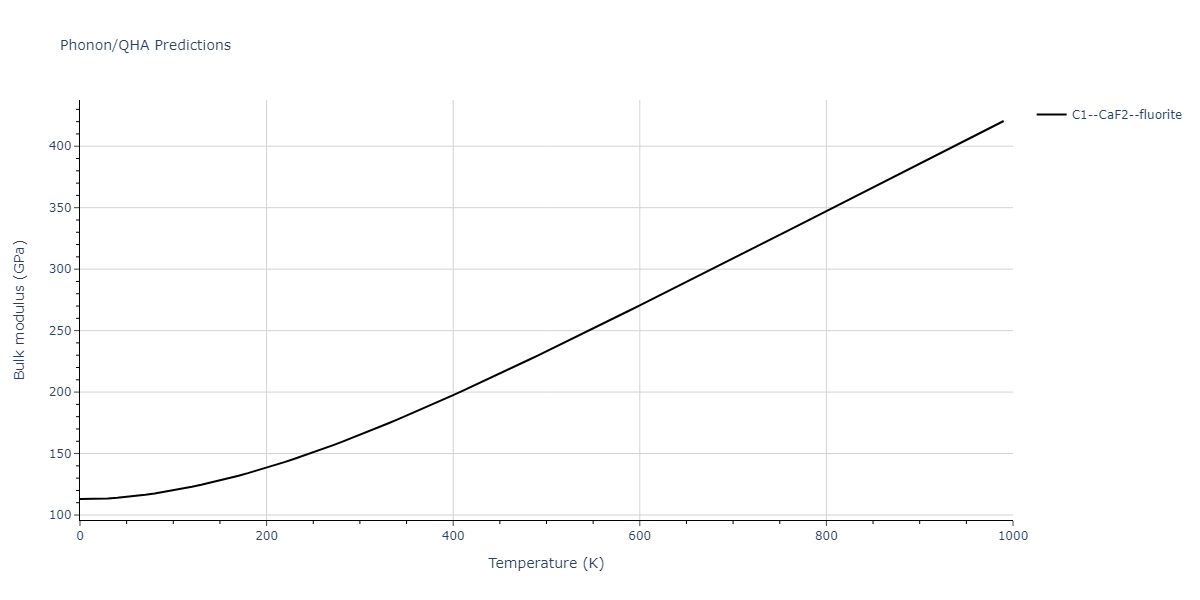
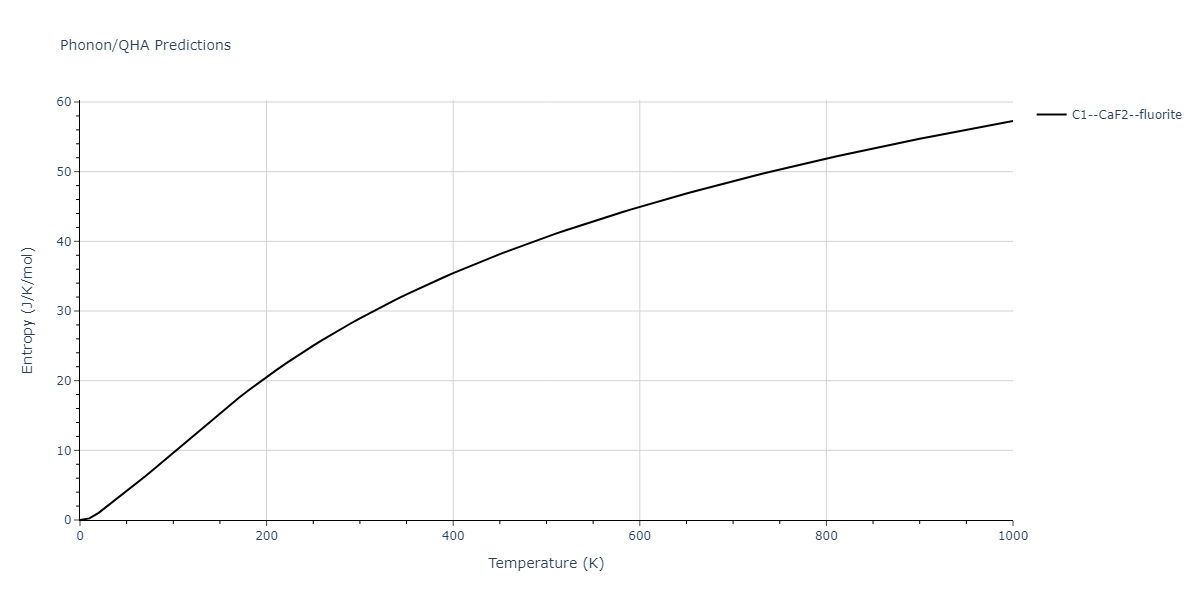
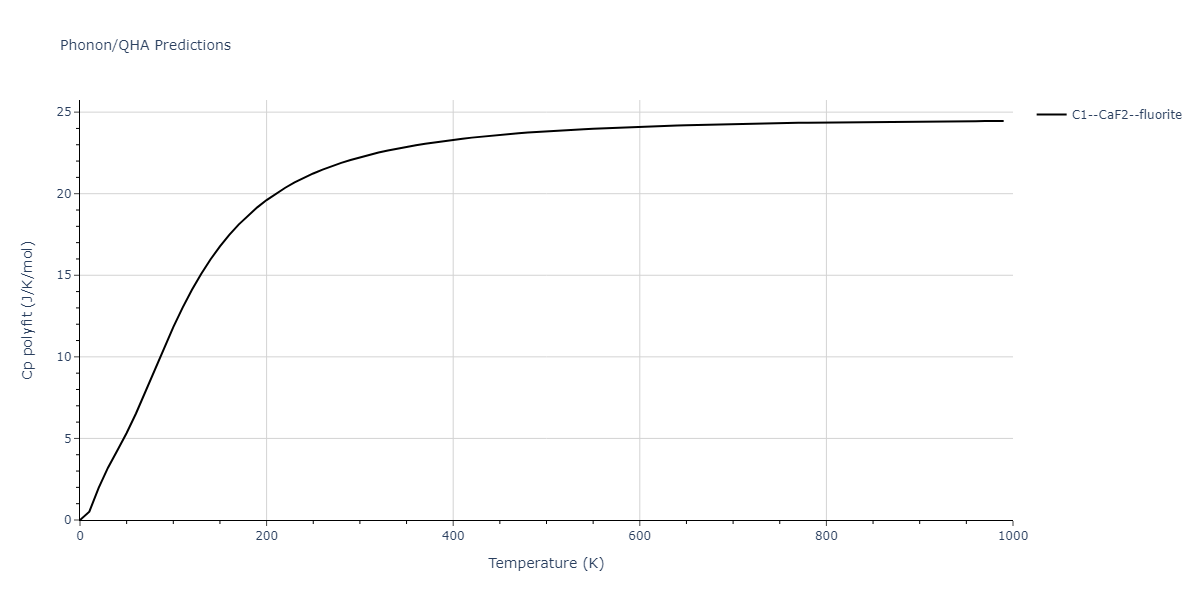
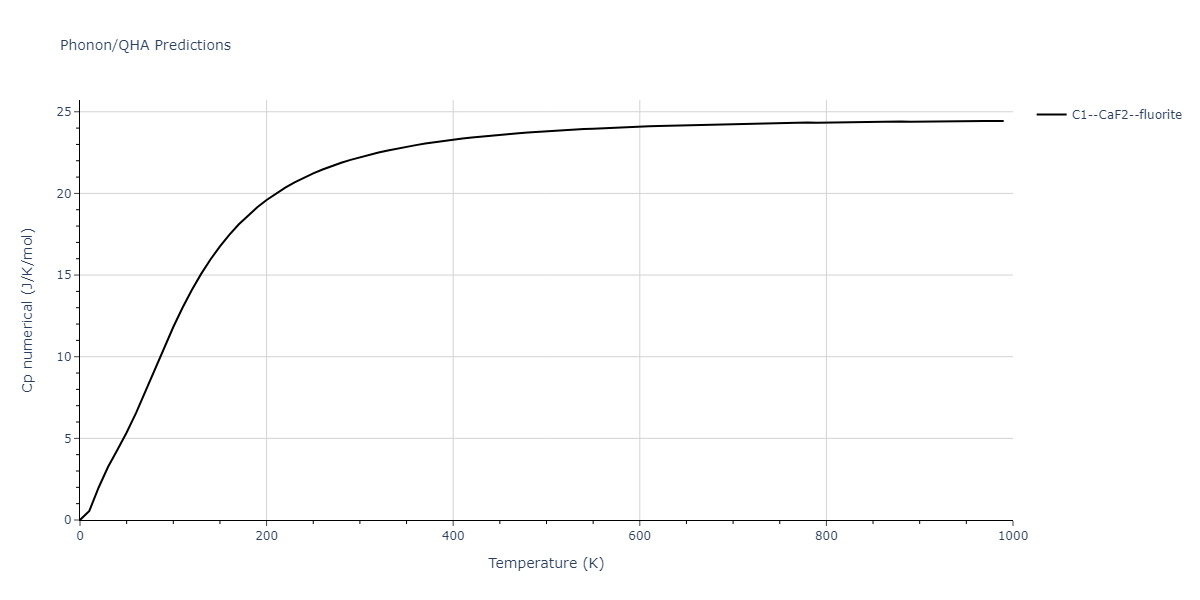
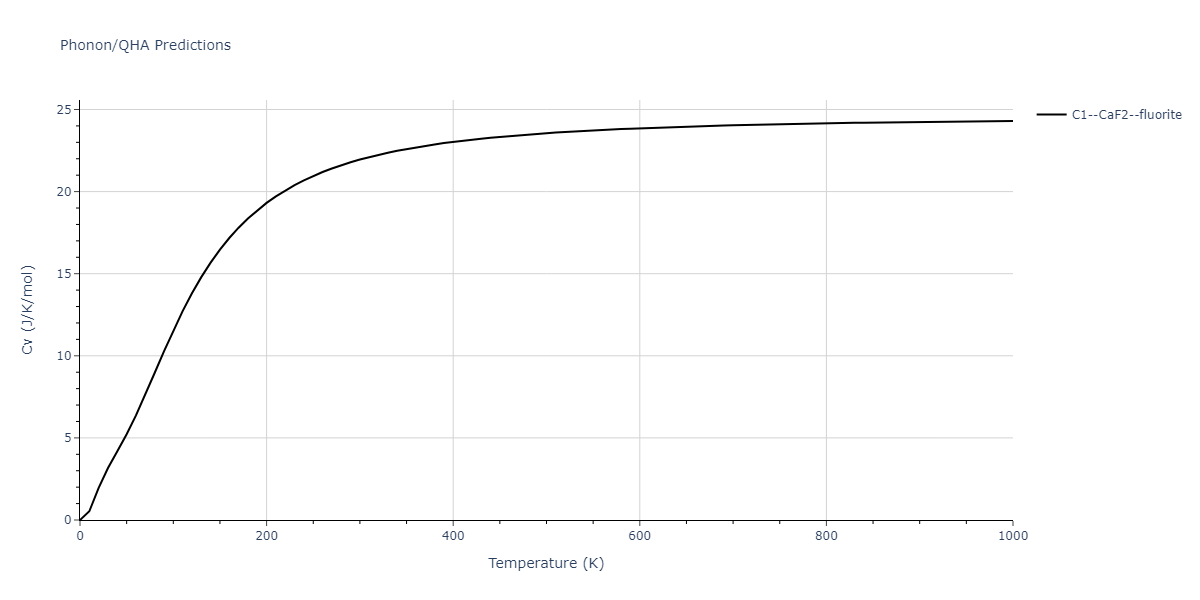
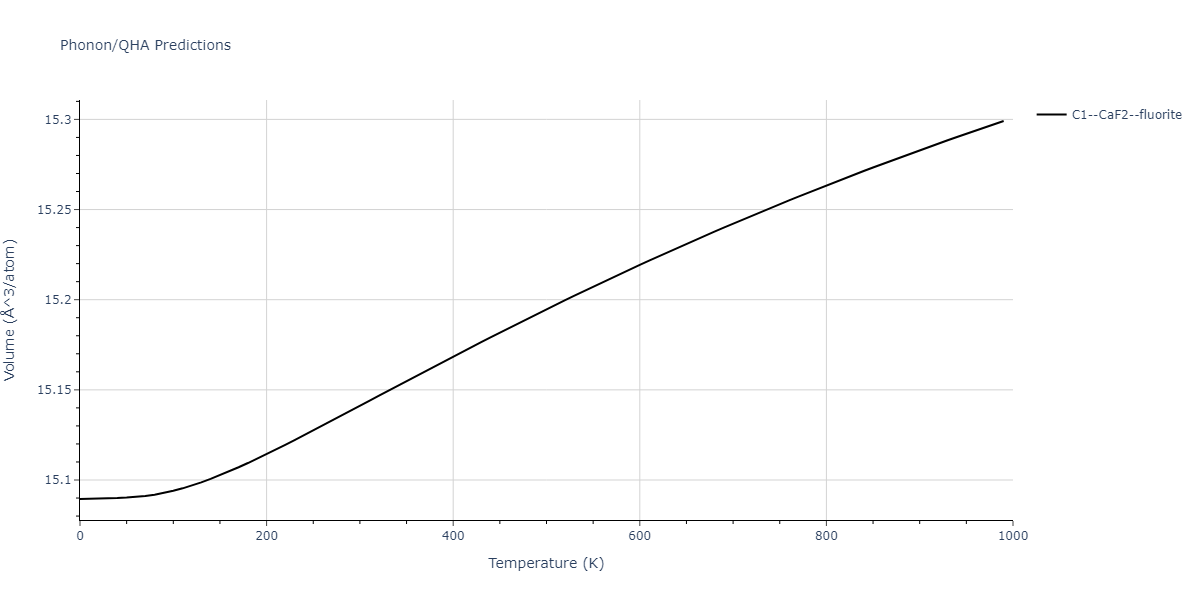
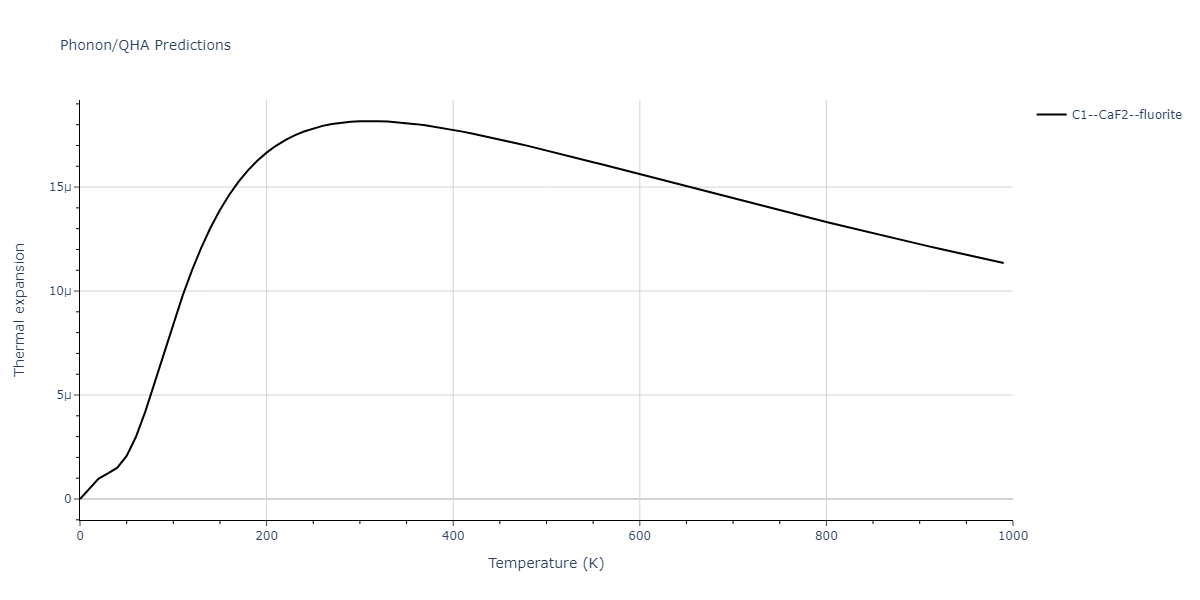
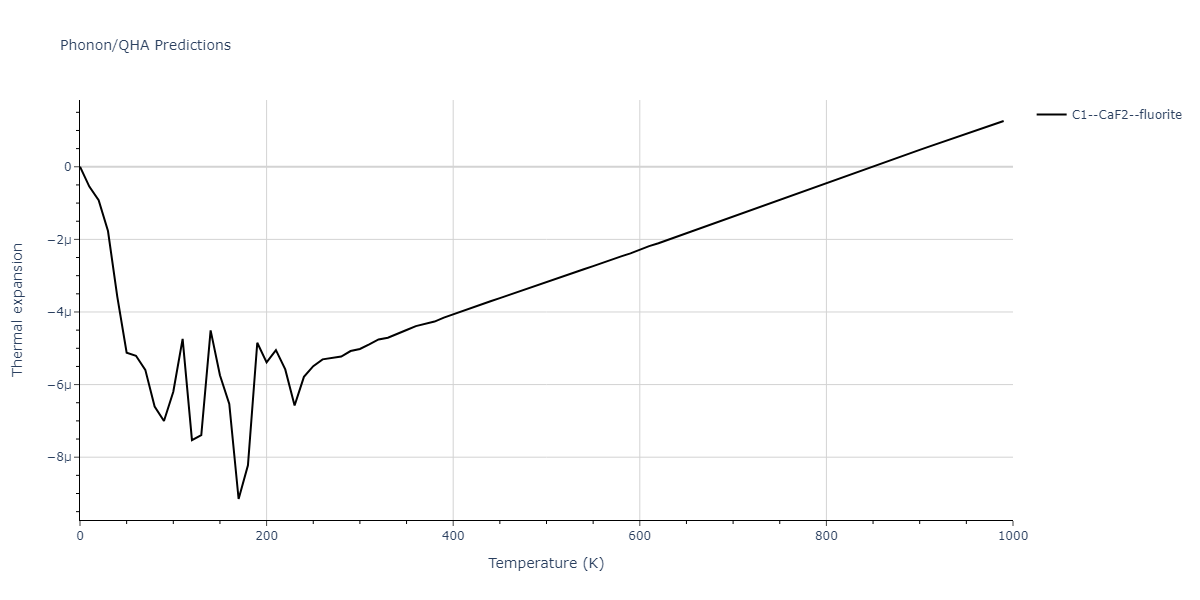
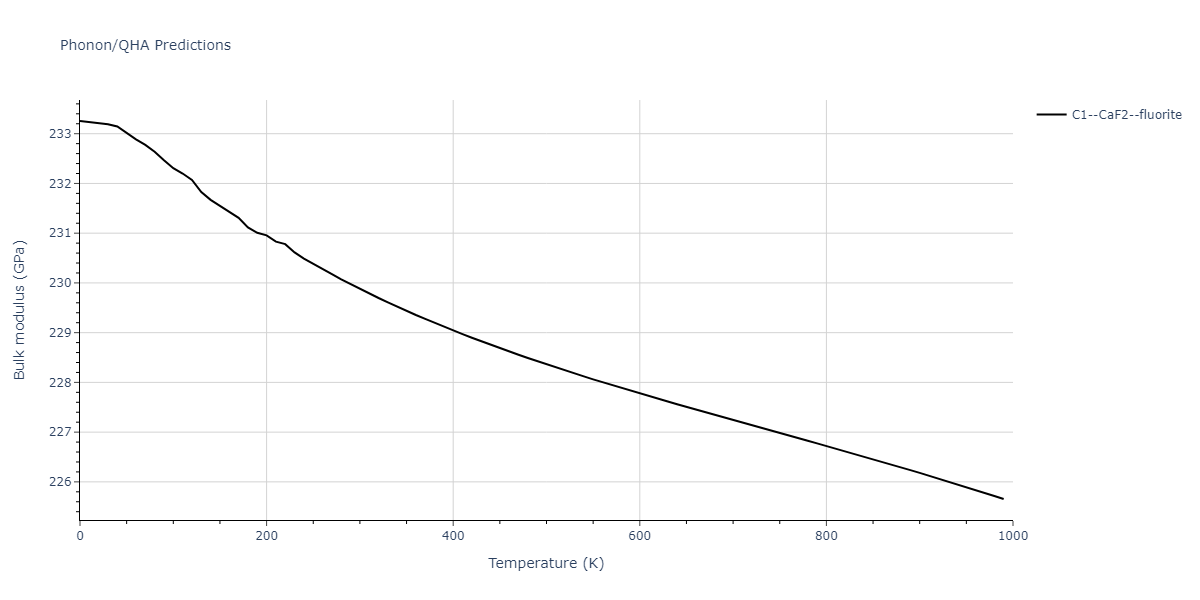
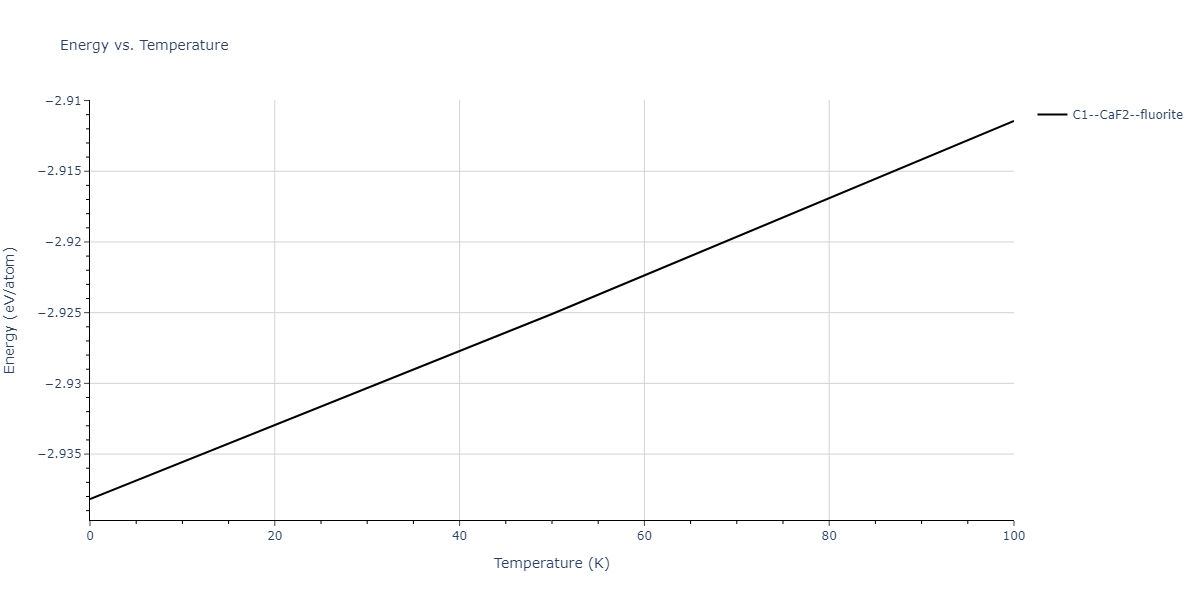
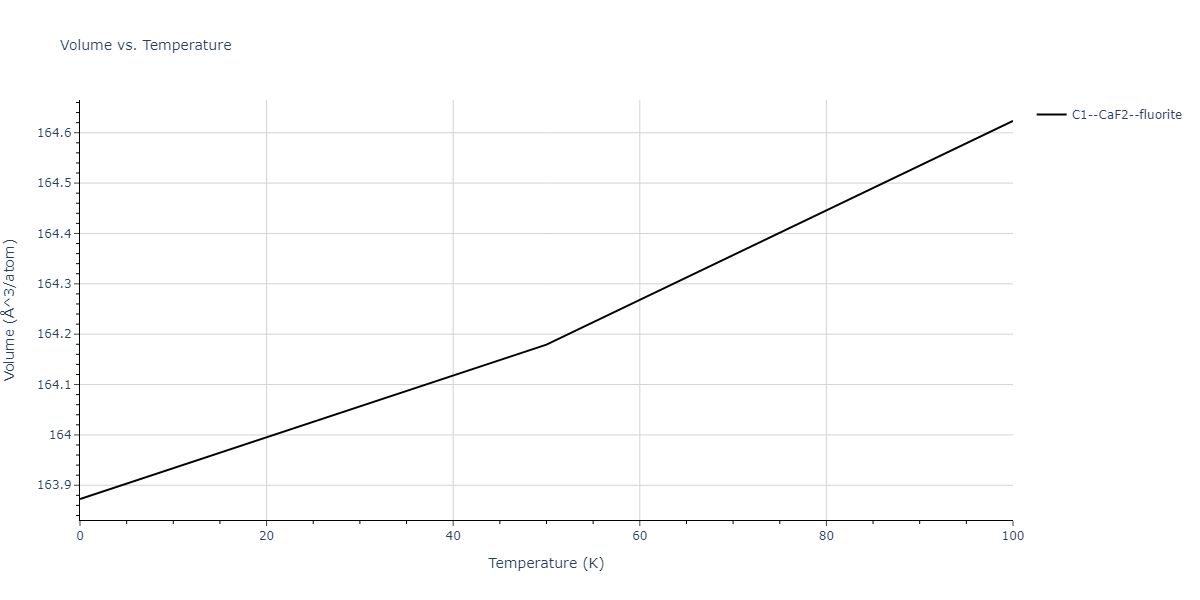
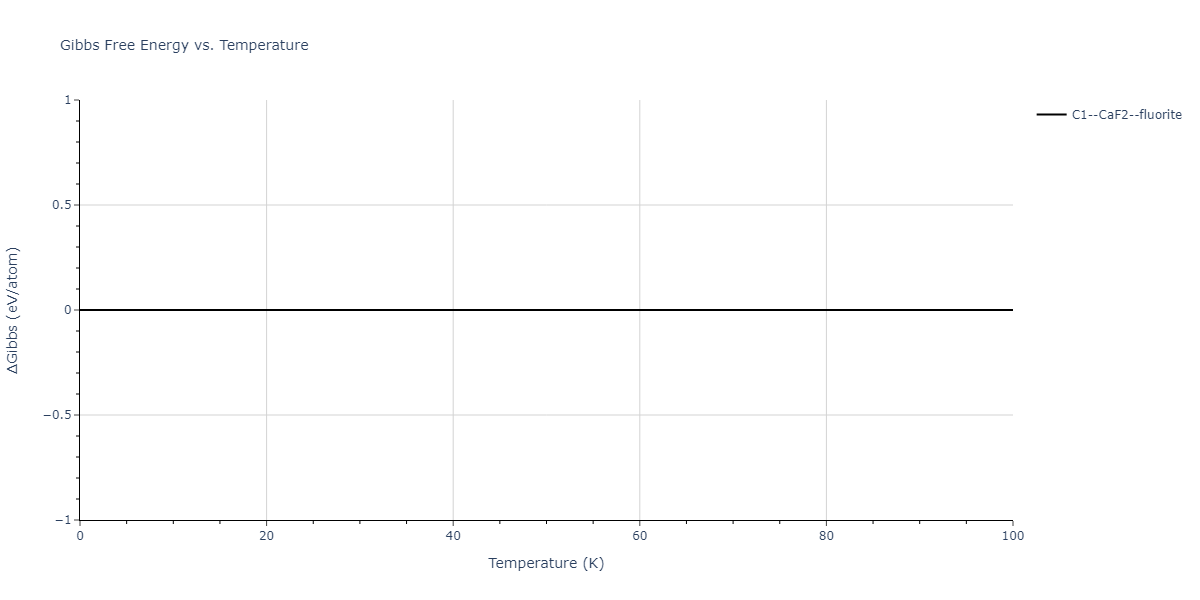
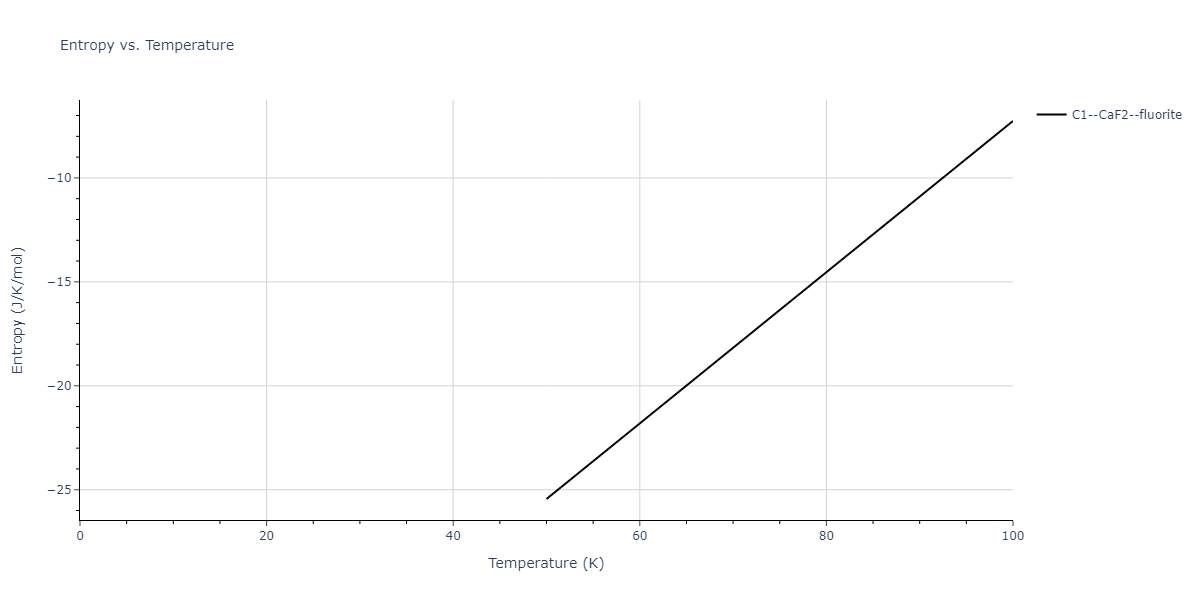
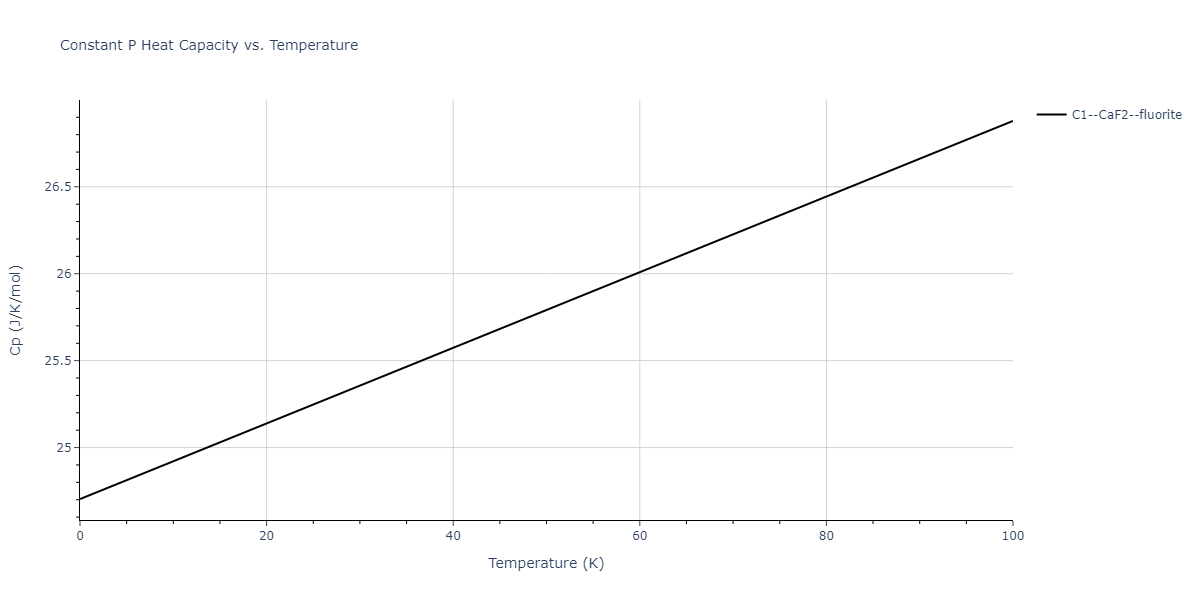
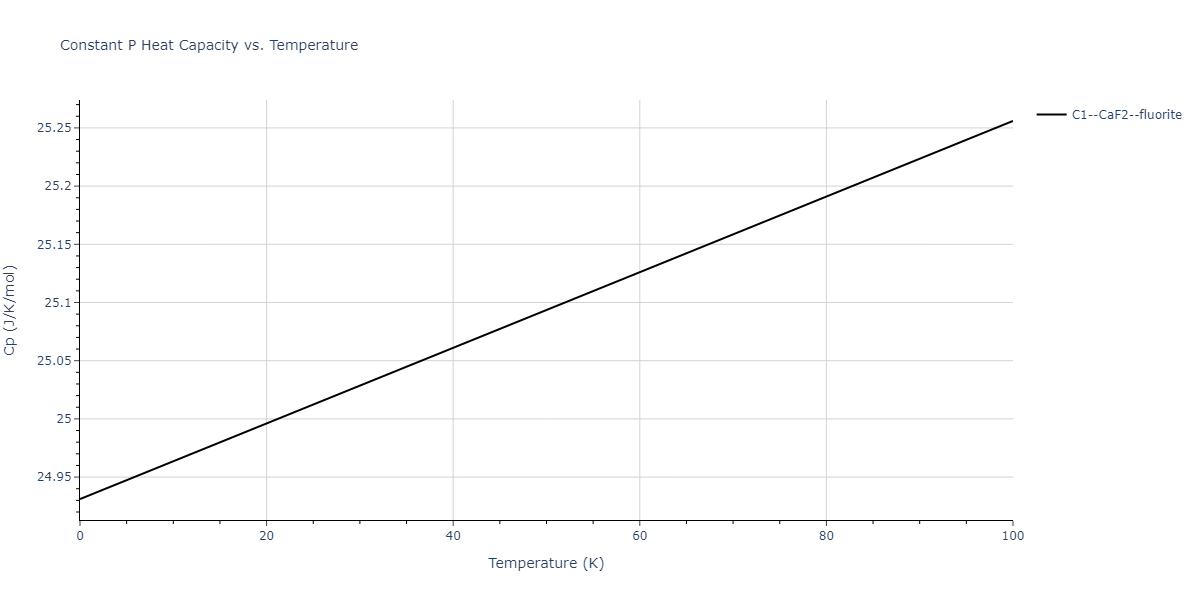
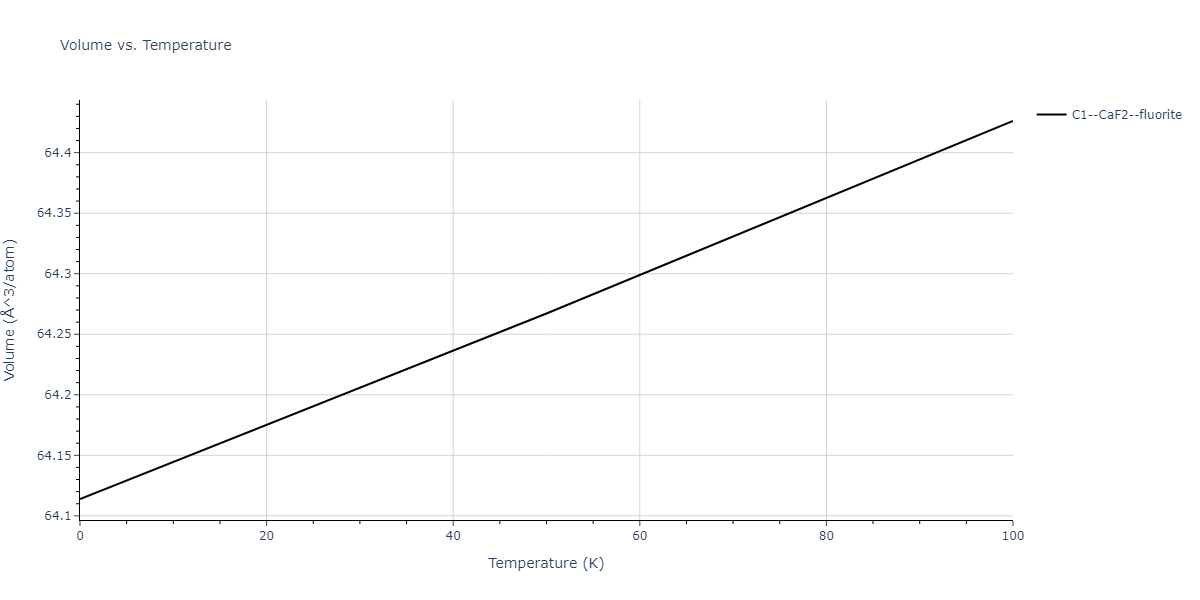
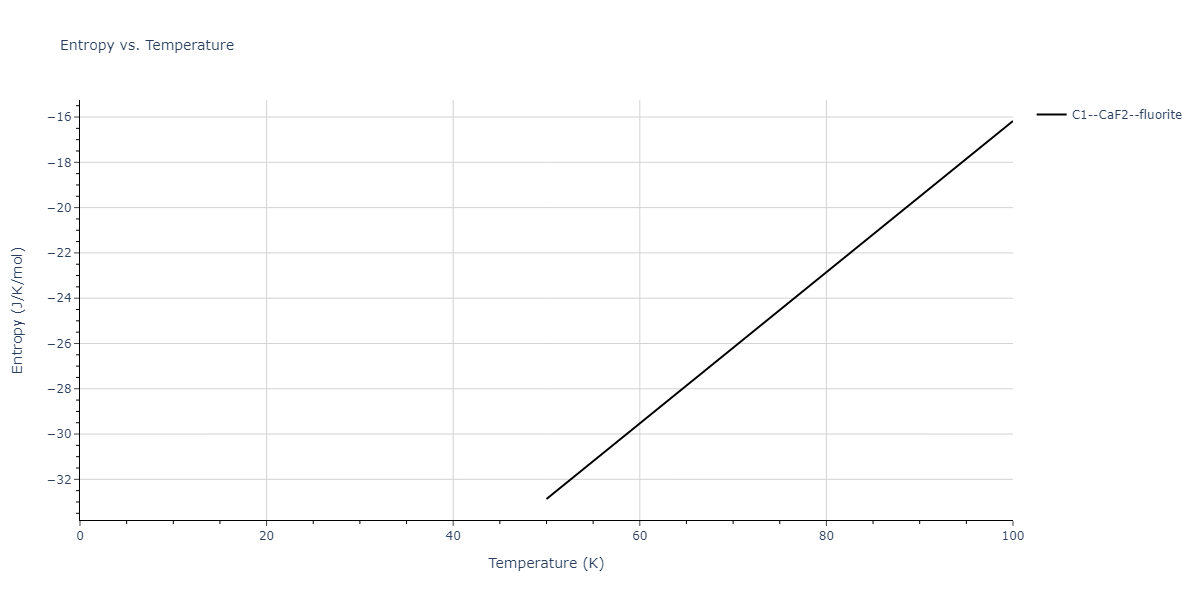
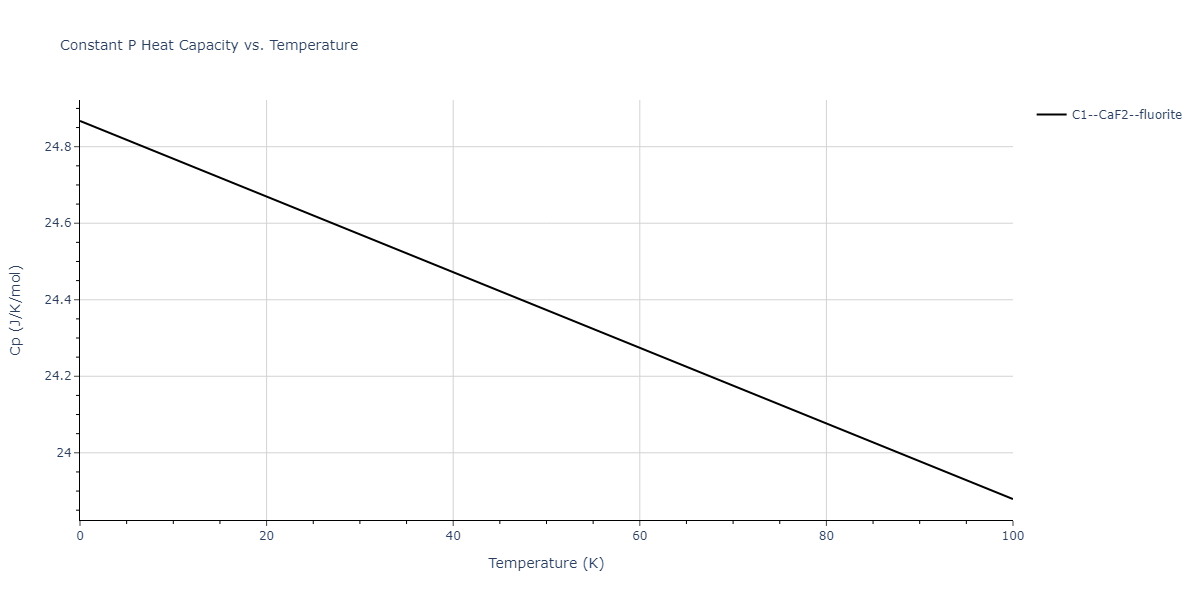
| C1--CaF2--fluorite | dynamic | -2.9382 | -2.9382 | 5.4723 | 5.4723 | 5.4723 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
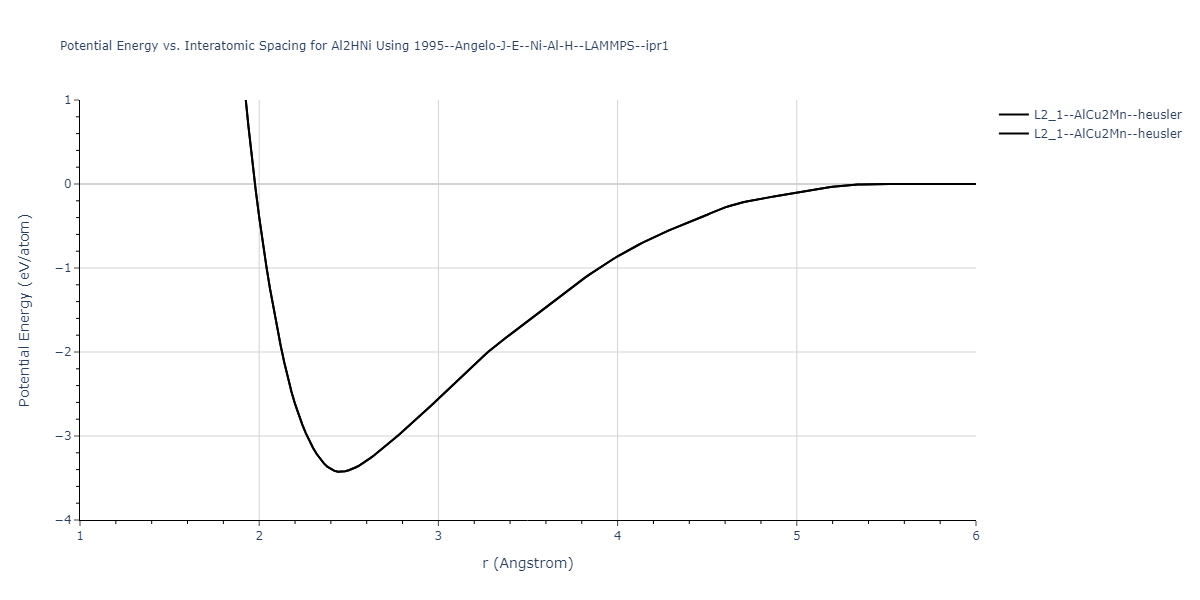
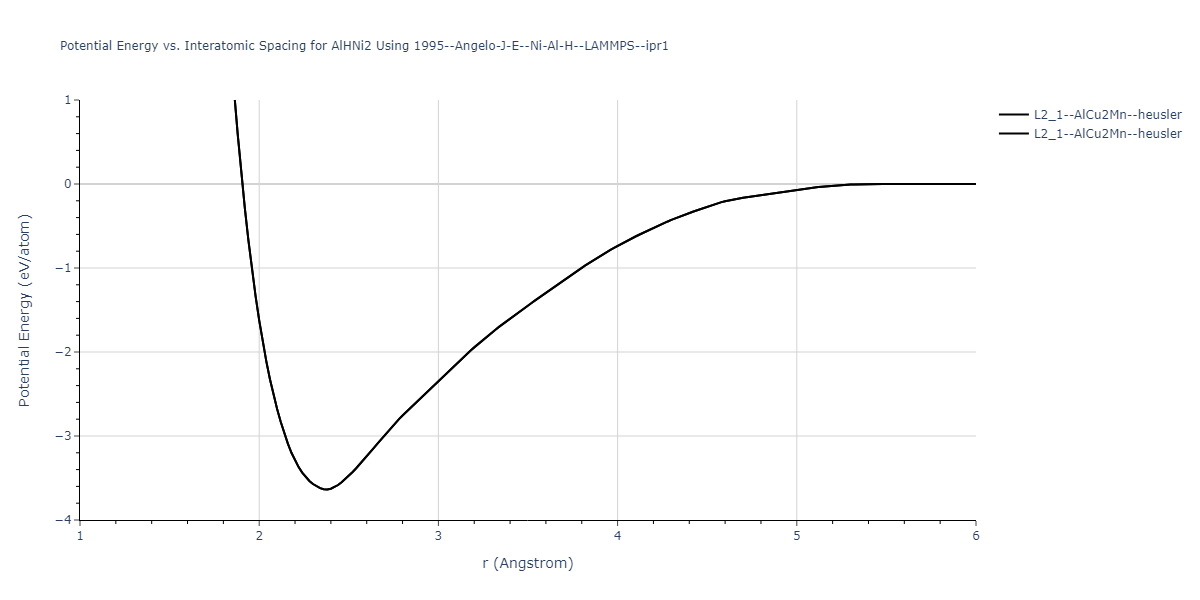
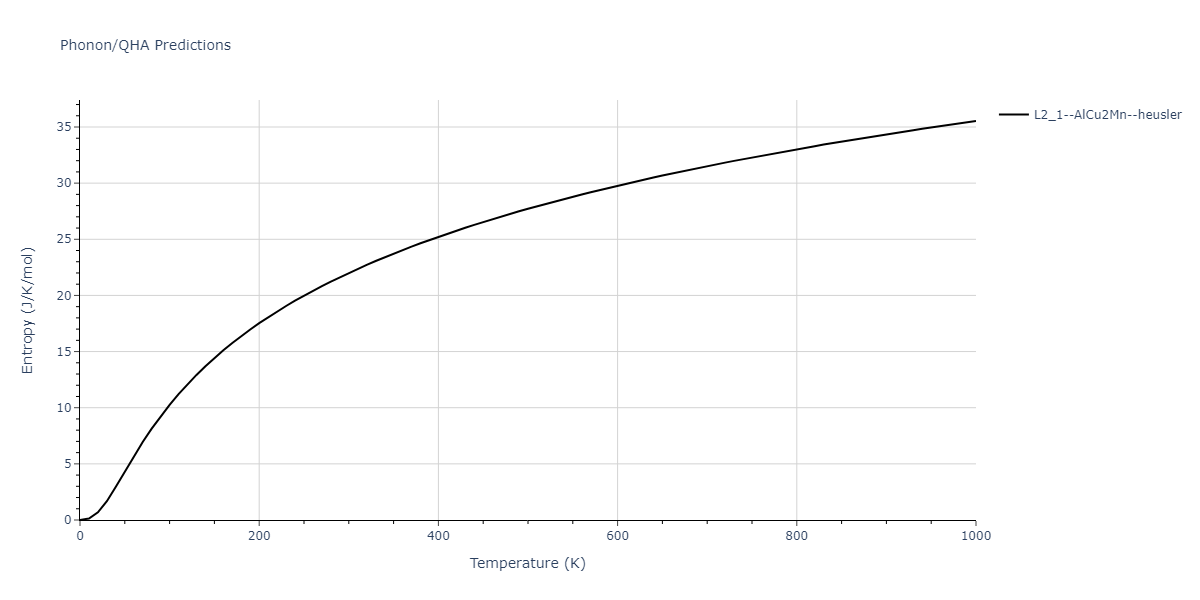
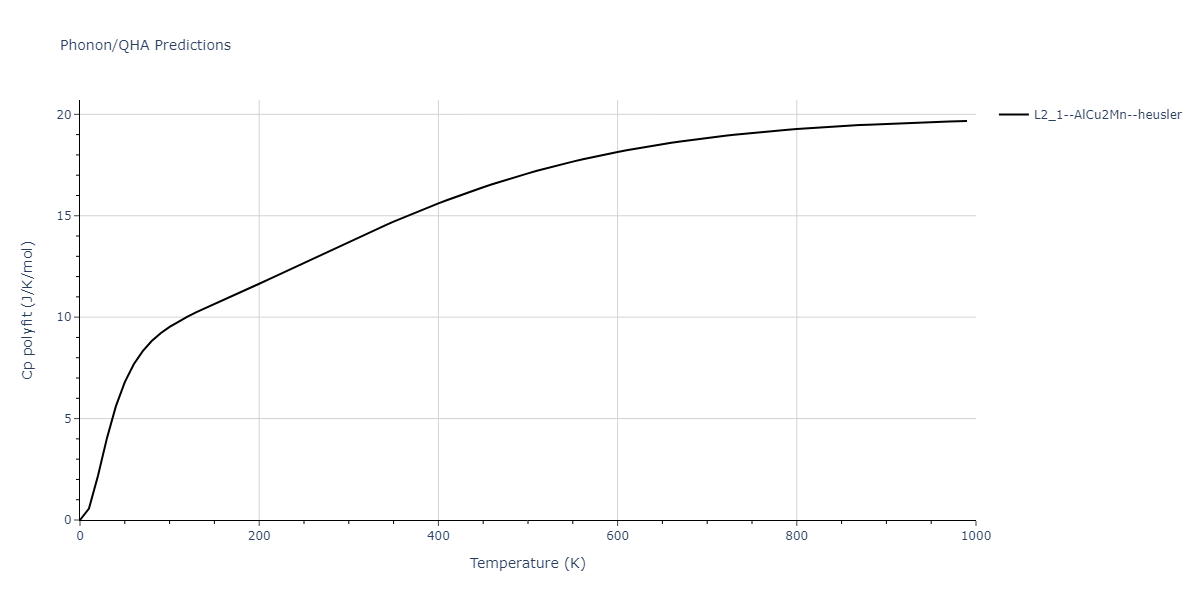
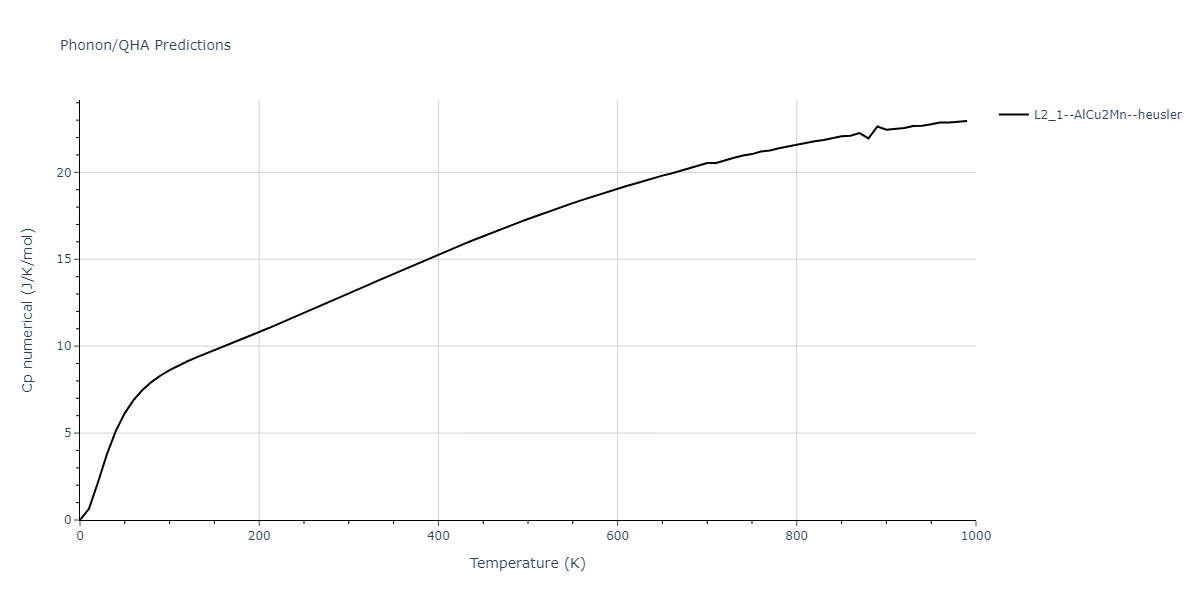
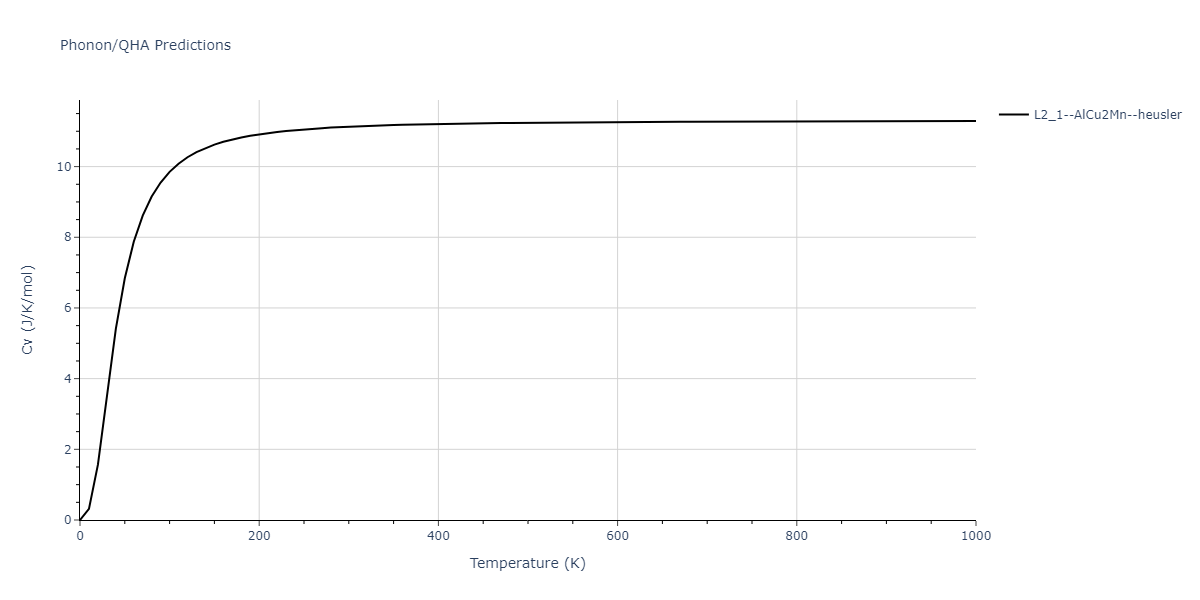
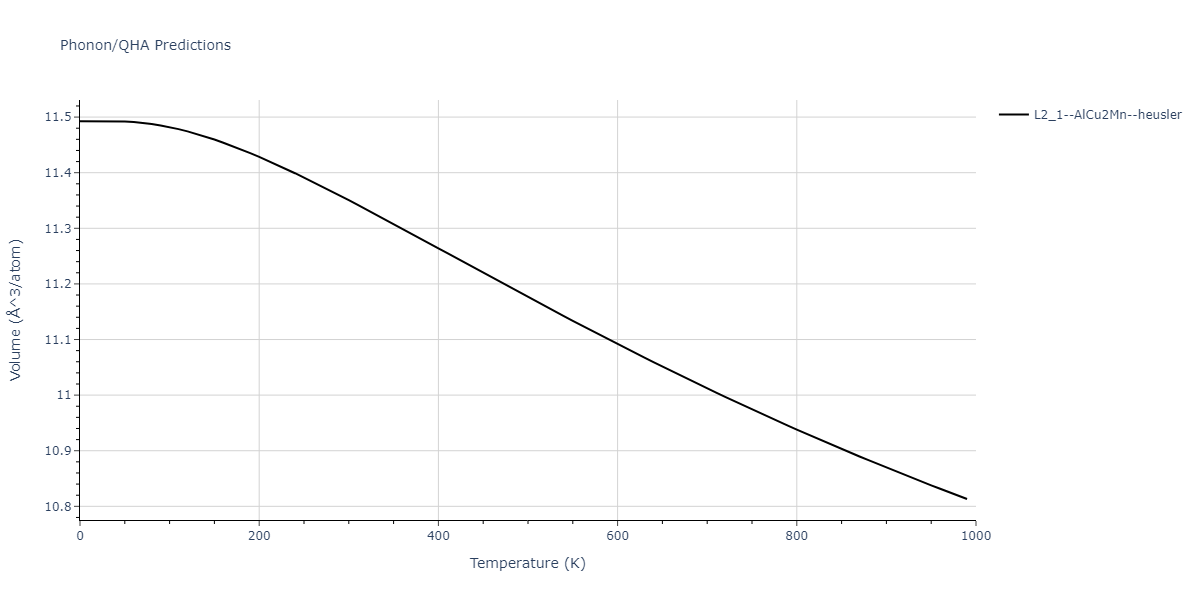
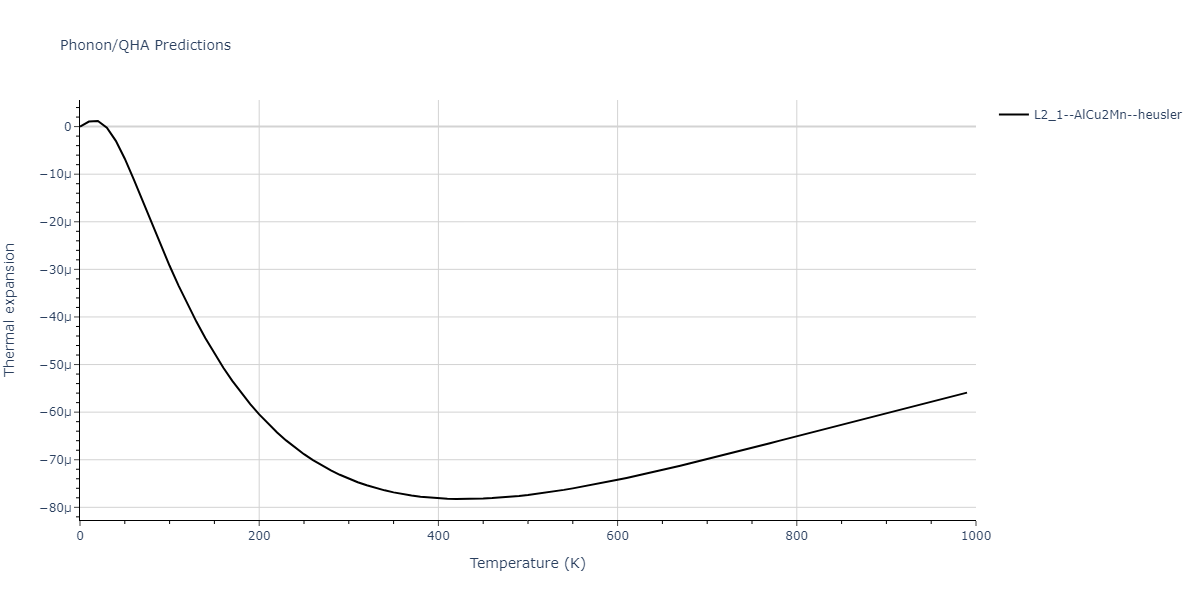
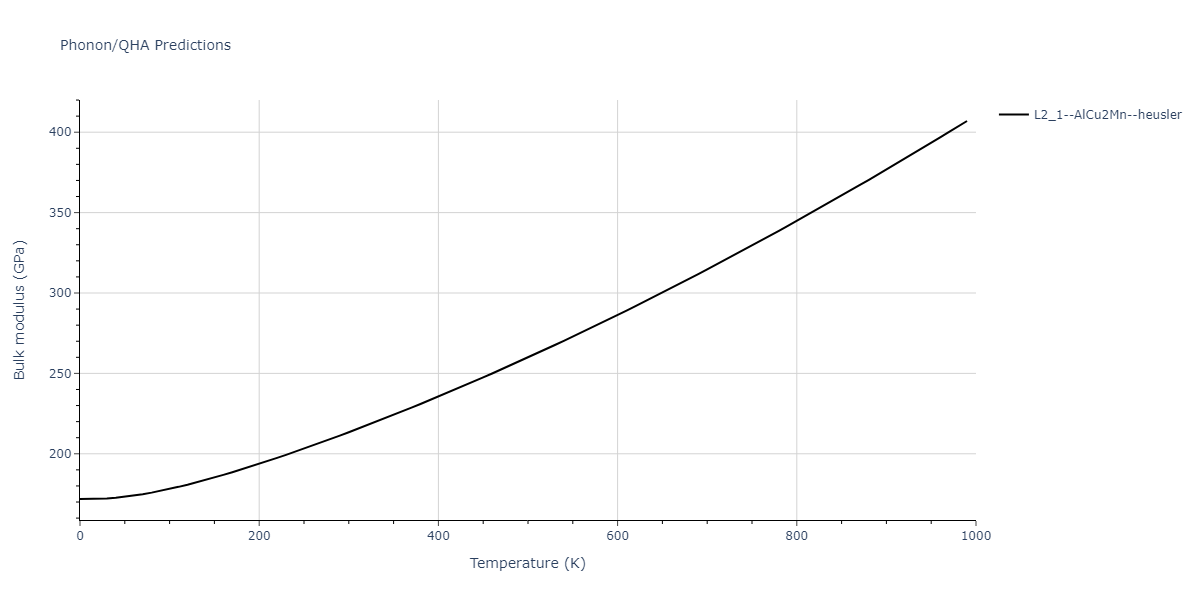
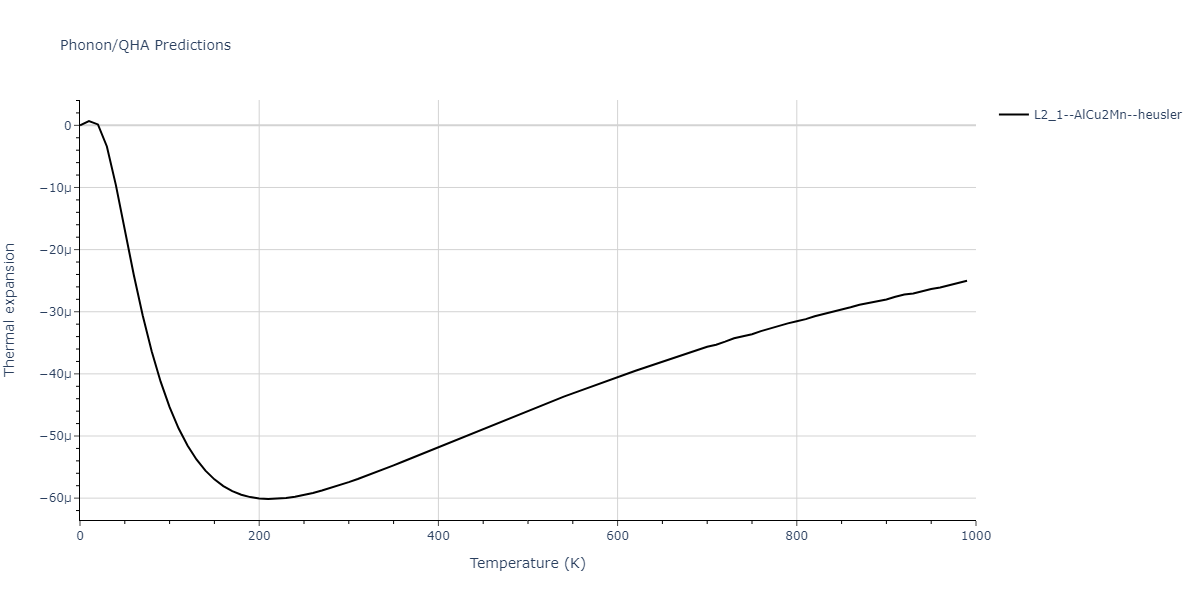
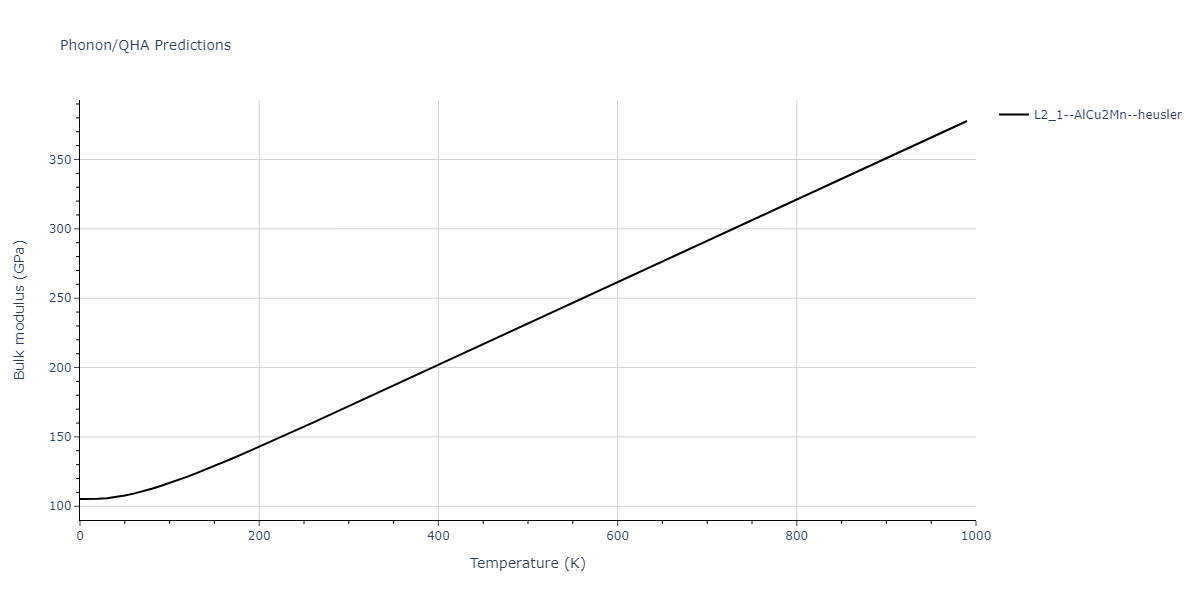
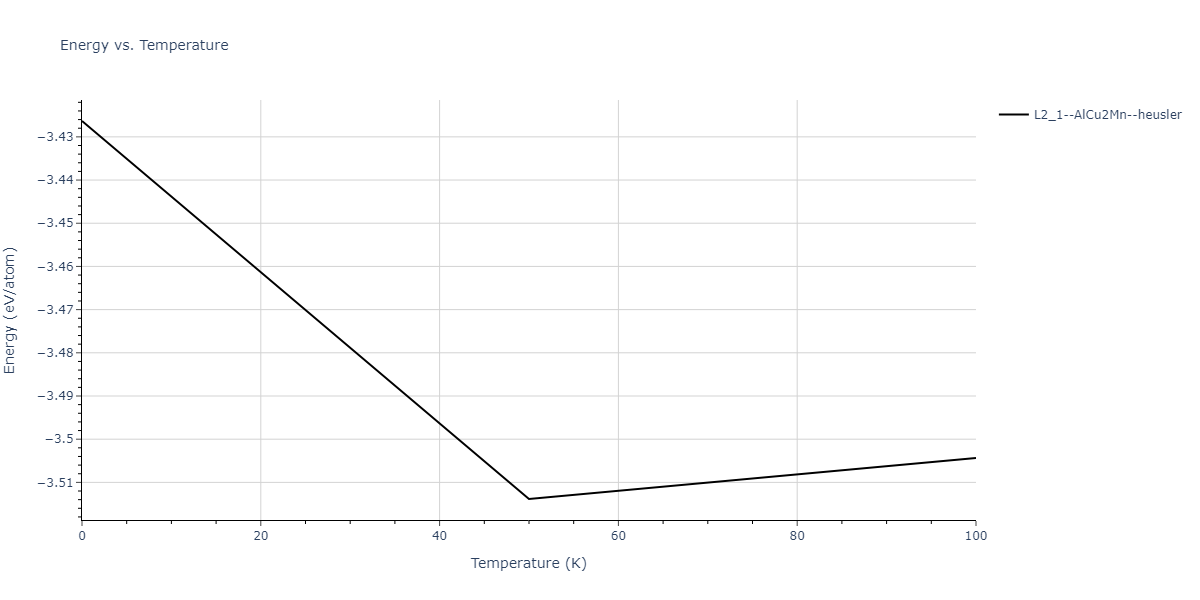
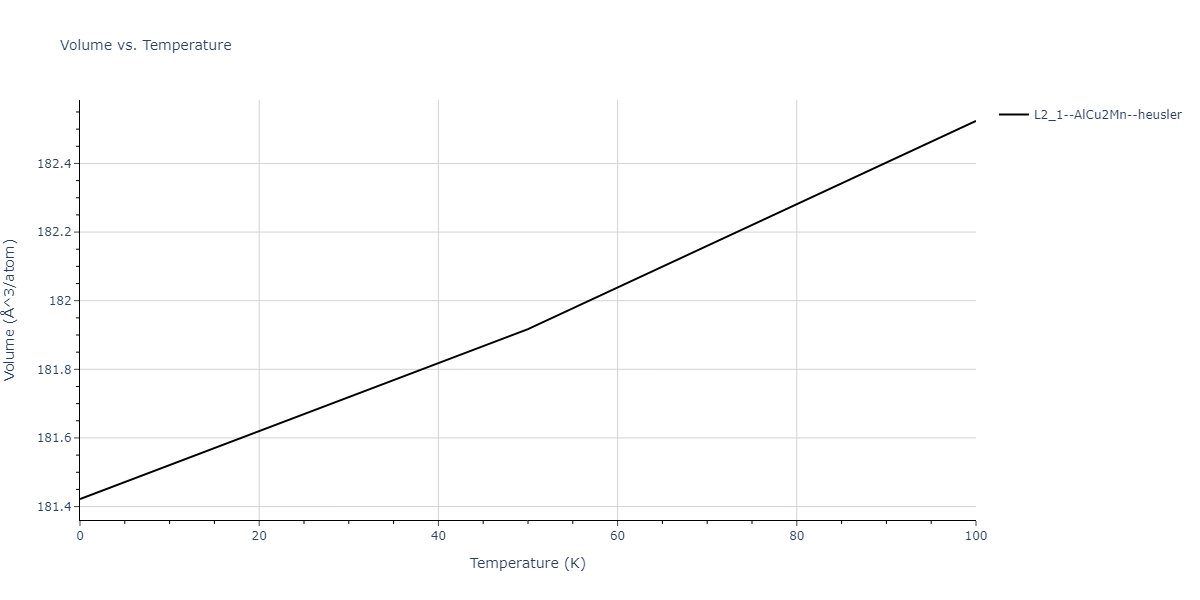
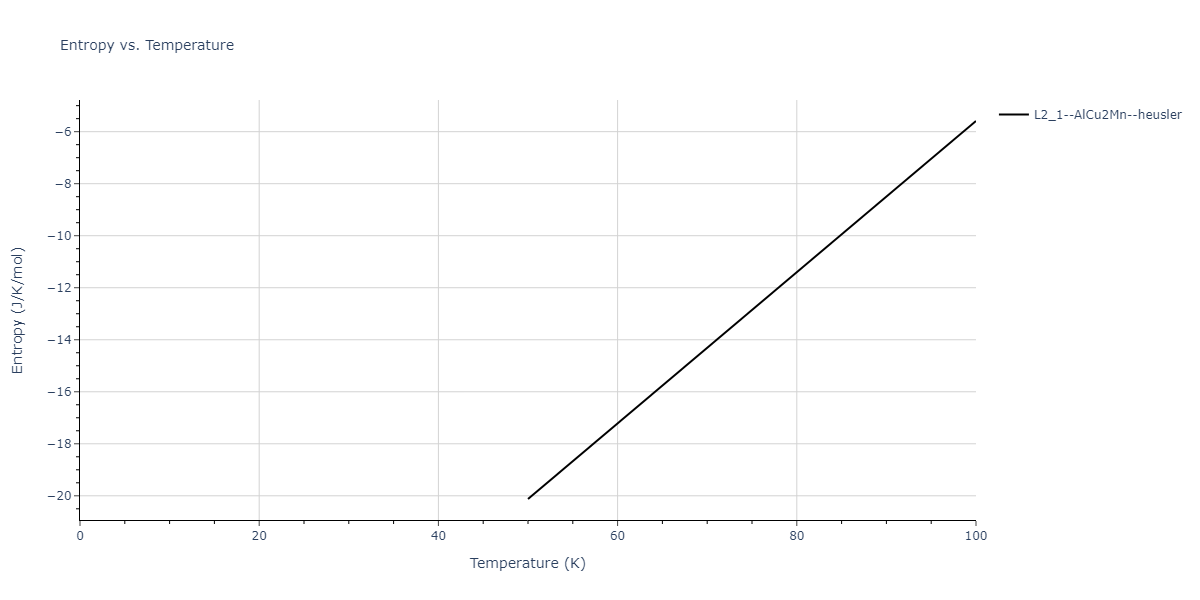
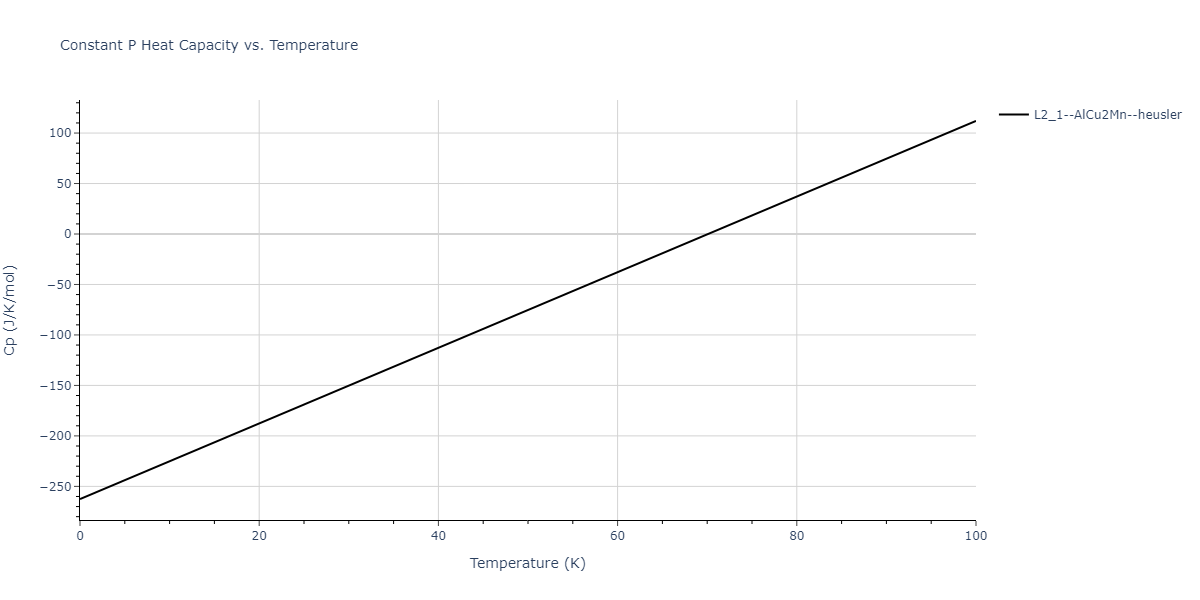
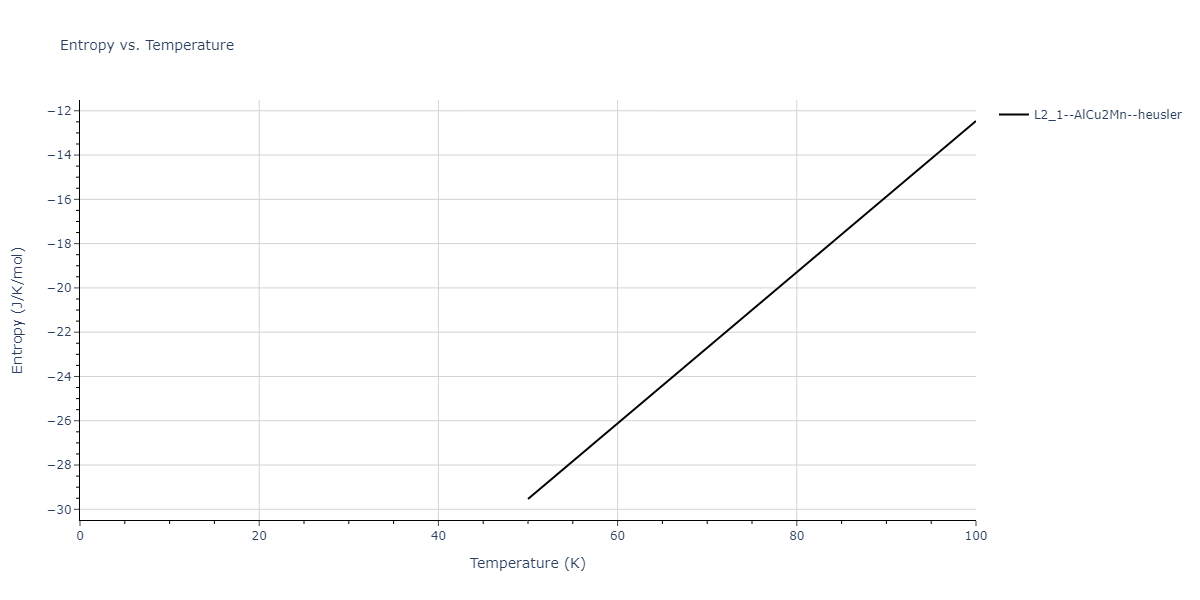
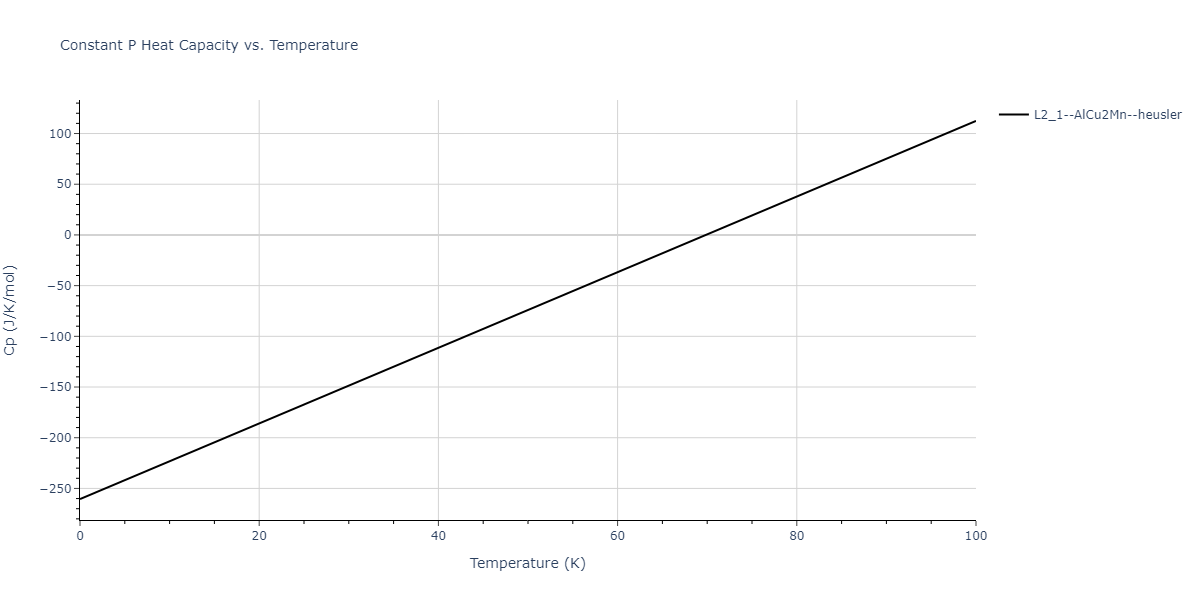
| L2_1--AlCu2Mn--heusler | dynamic | -3.4263 | -3.4263 | 5.661 | 5.661 | 5.661 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
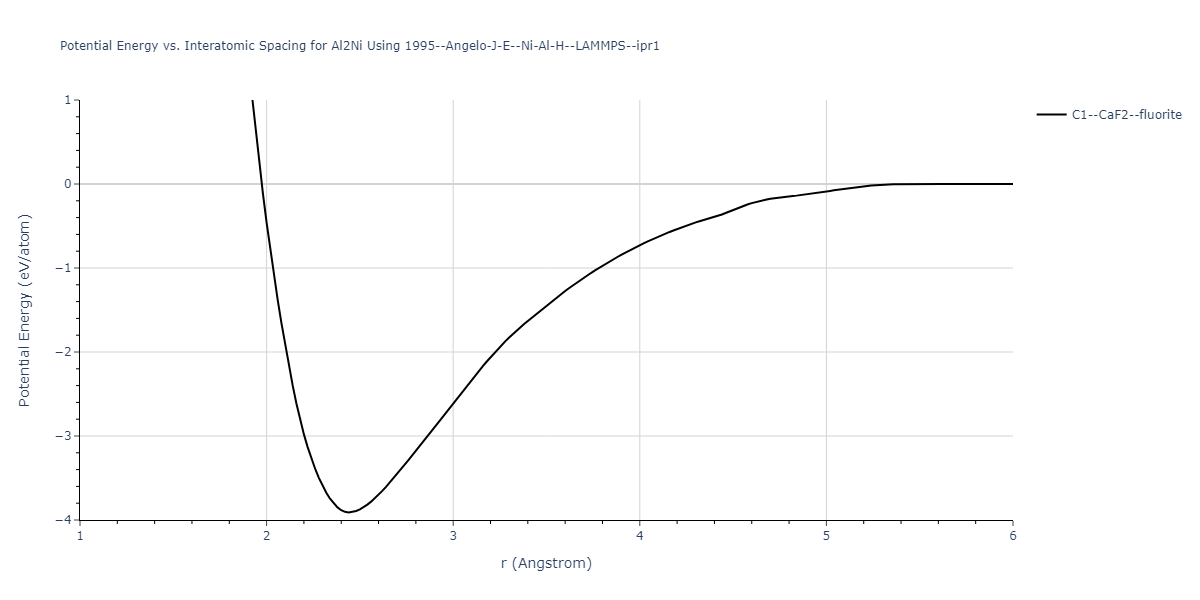
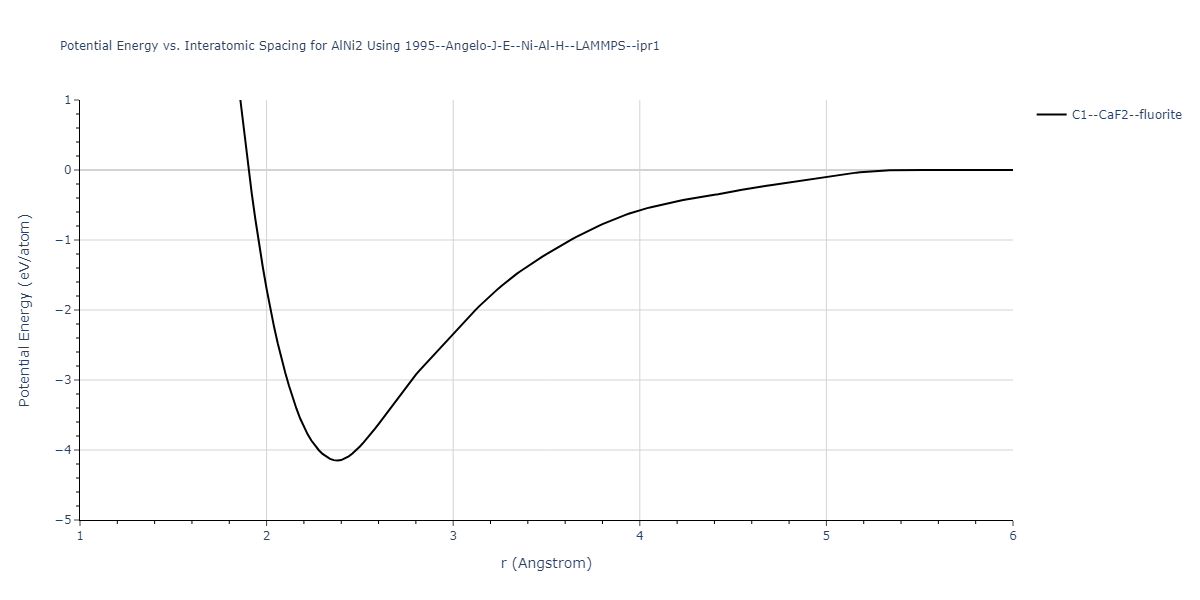
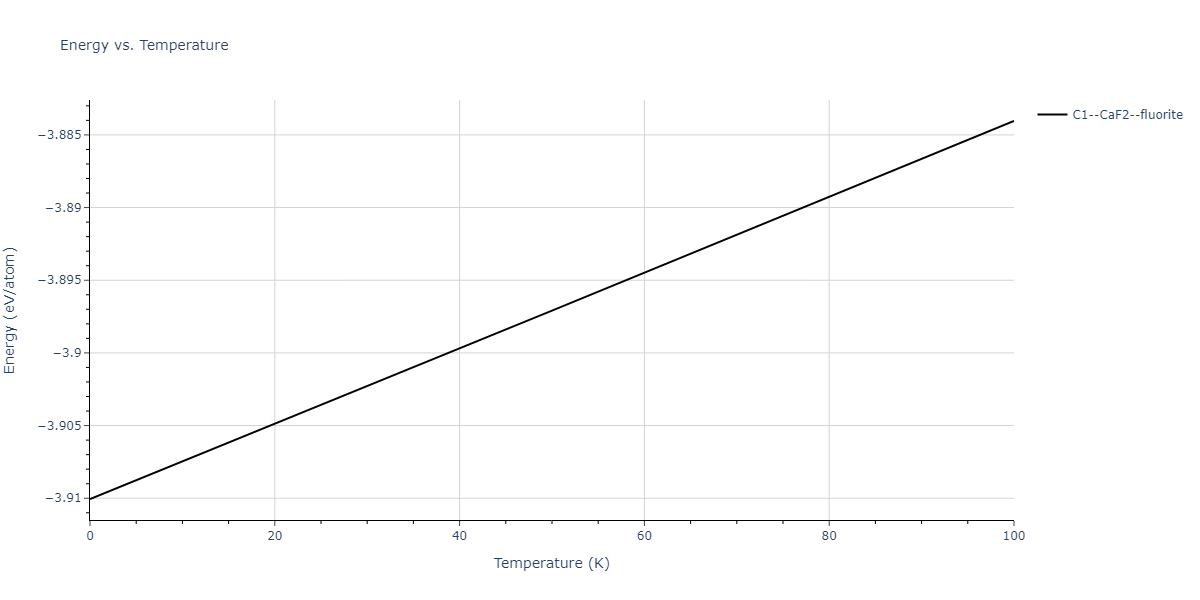
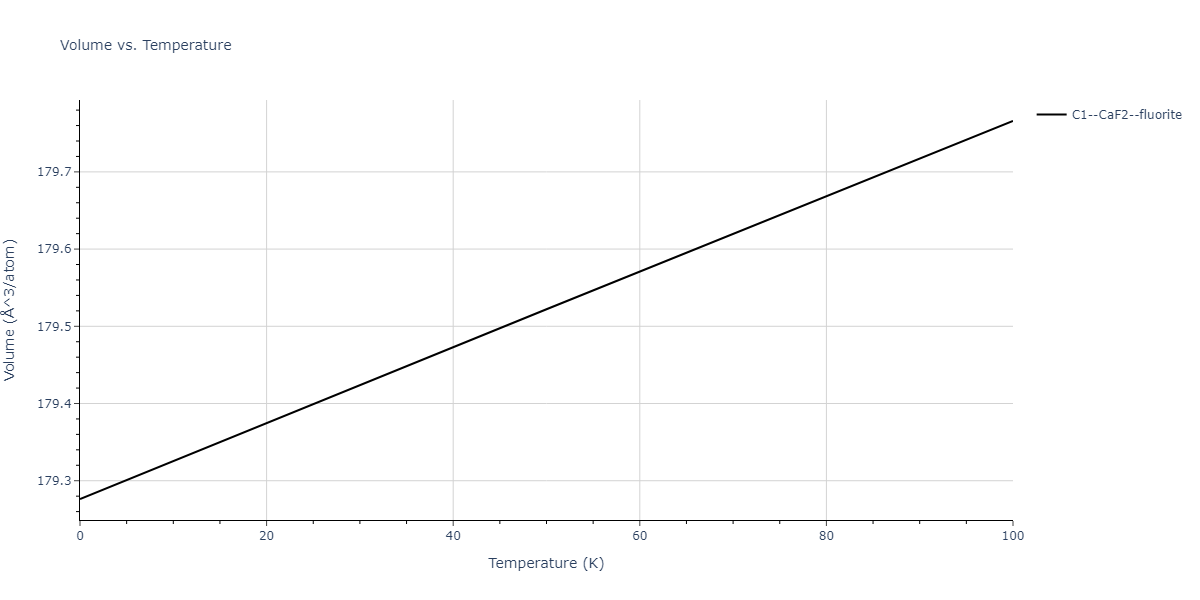
| C1--CaF2--fluorite | dynamic | -3.9101 | -3.9101 | 5.6386 | 5.6386 | 5.6386 | 90.0 | 90.0 | 90.0 |
| oqmd-1231494 | box | -3.592 | -3.592 | 6.2591 | 6.2591 | 2.6316 | 90.0 | 90.0 | 90.0 |
| oqmd-1239581 | static | -2.1005 | -2.1005 | 10.4528 | 10.4528 | 10.4528 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-1229048 | dynamic | -4.4609 | -4.4609 | 2.893 | 2.893 | 13.9116 | 90.0 | 90.0 | 90.0 |
| mp-1229048 | box | -4.4597 | -4.4597 | 2.9004 | 2.9004 | 13.8245 | 90.0 | 90.0 | 90.0 |
| oqmd-425572 | box | -4.1193 | -4.1193 | 6.2355 | 6.2355 | 12.3091 | 90.0 | 90.0 | 120.0 |
Download raw data (including filtered results)
Reference structure matches:
D0_3--BiF3 = mp-1183138, oqmd-313157
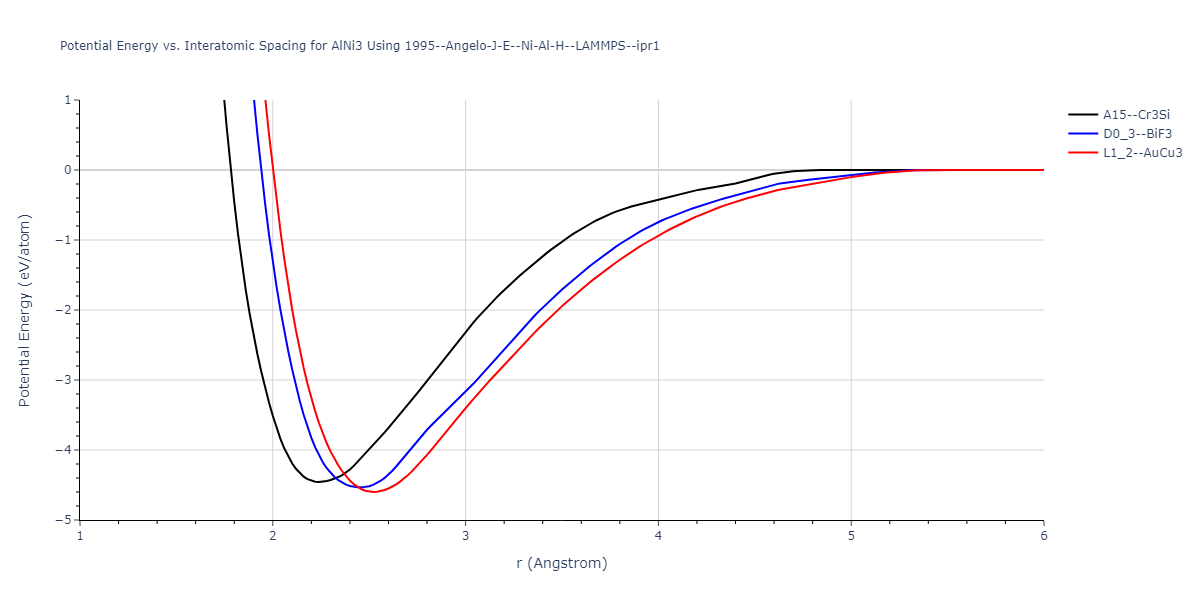
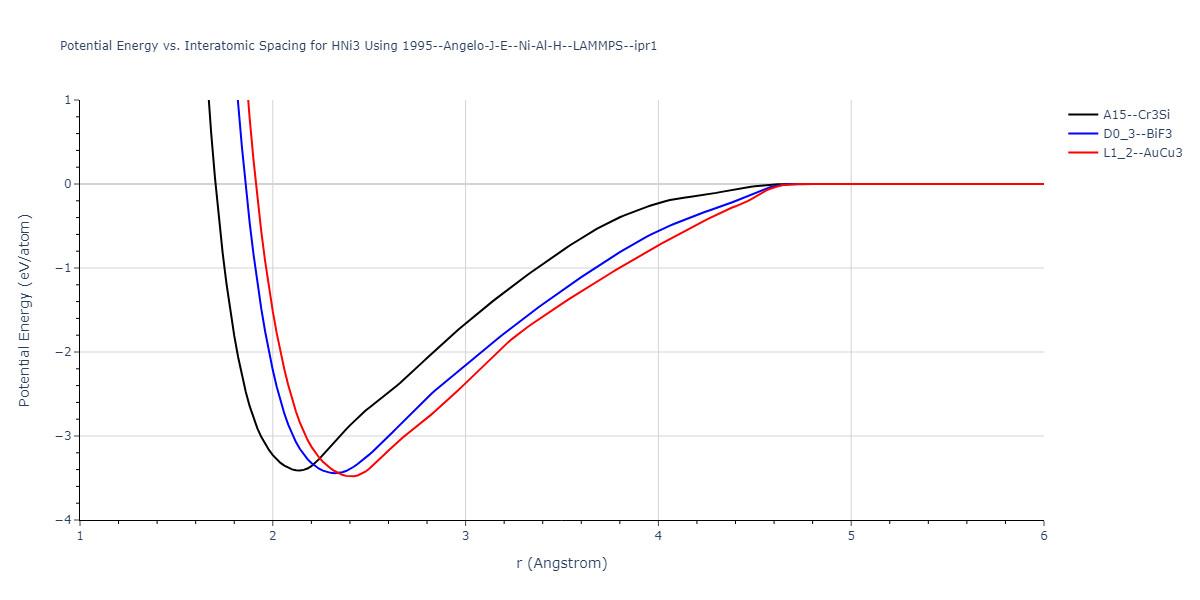
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| oqmd-302615 | box | -2.9468 | -2.9468 | 3.9646 | 3.9646 | 7.5117 | 90.0 | 90.0 | 90.0 |
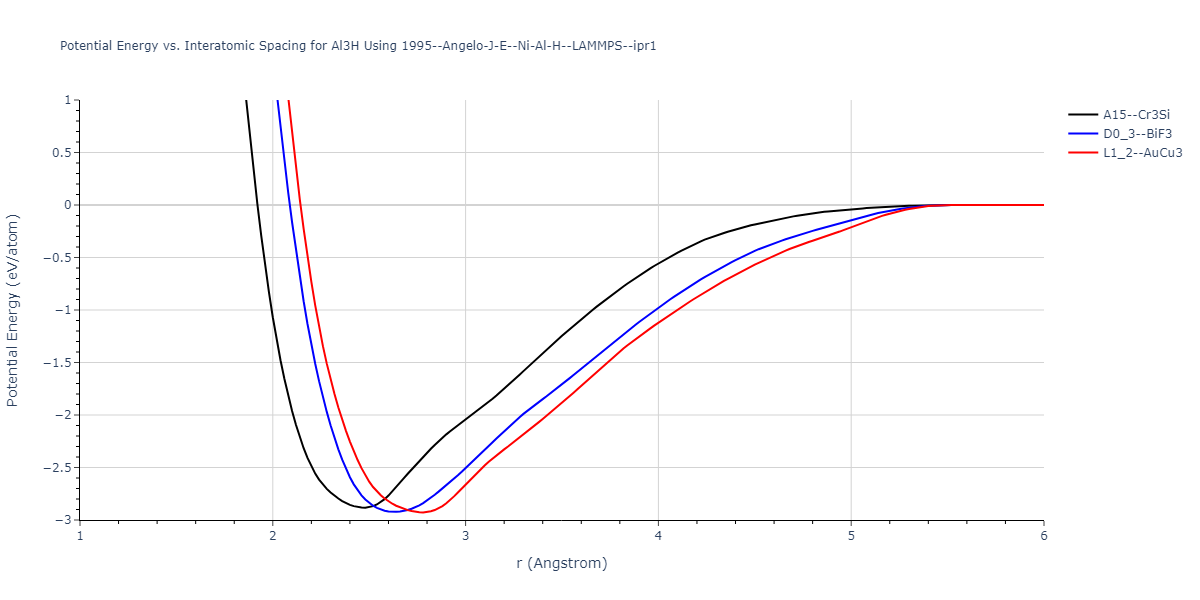
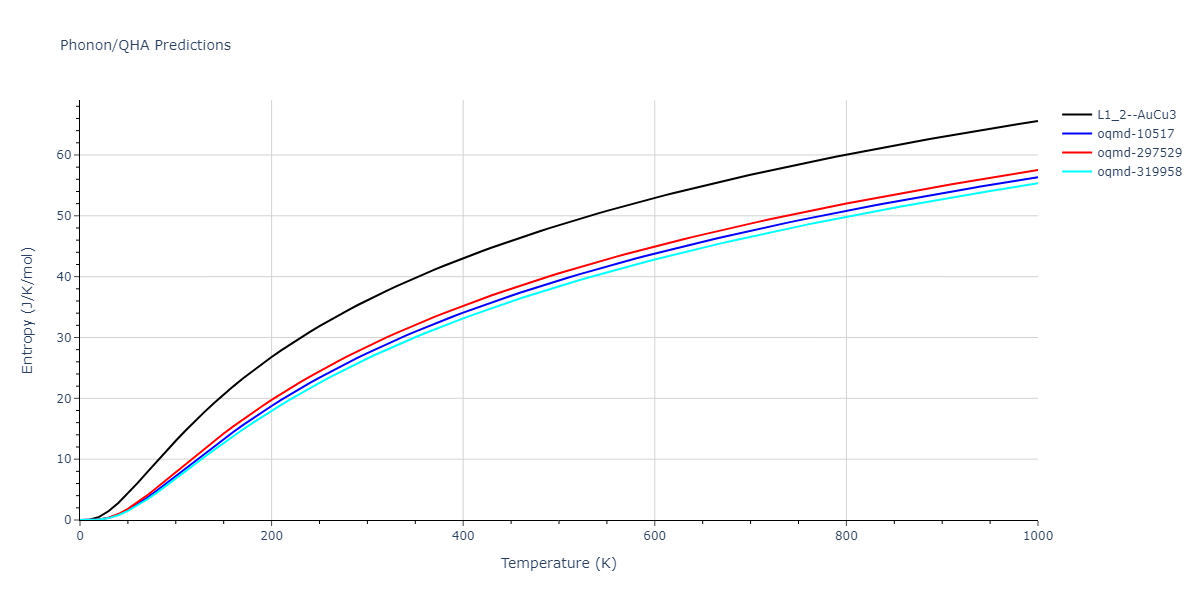
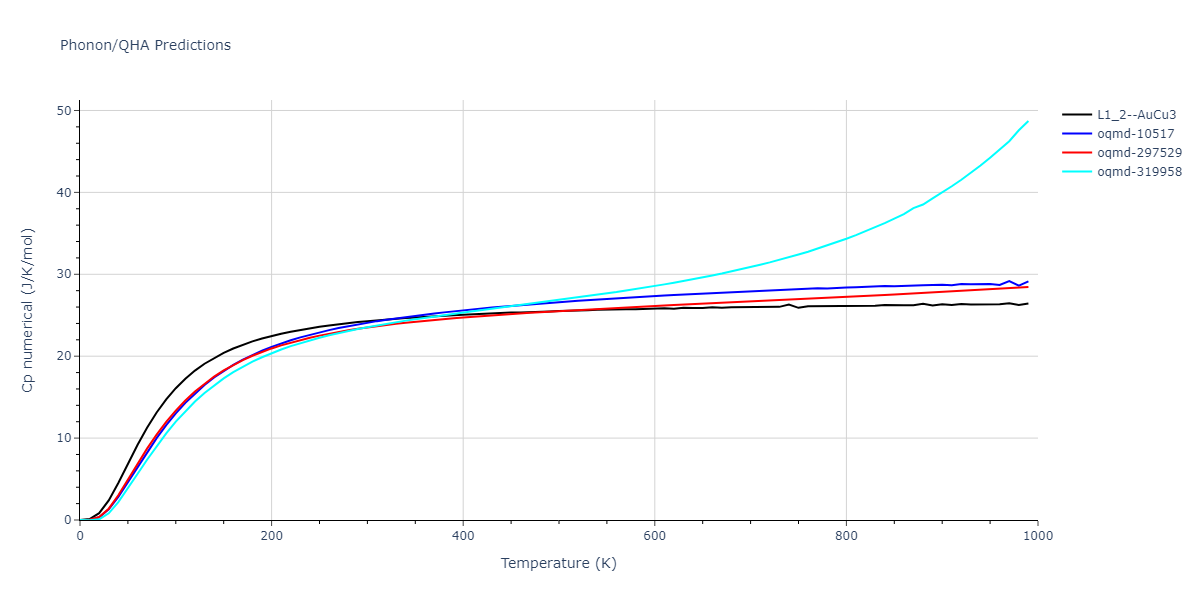
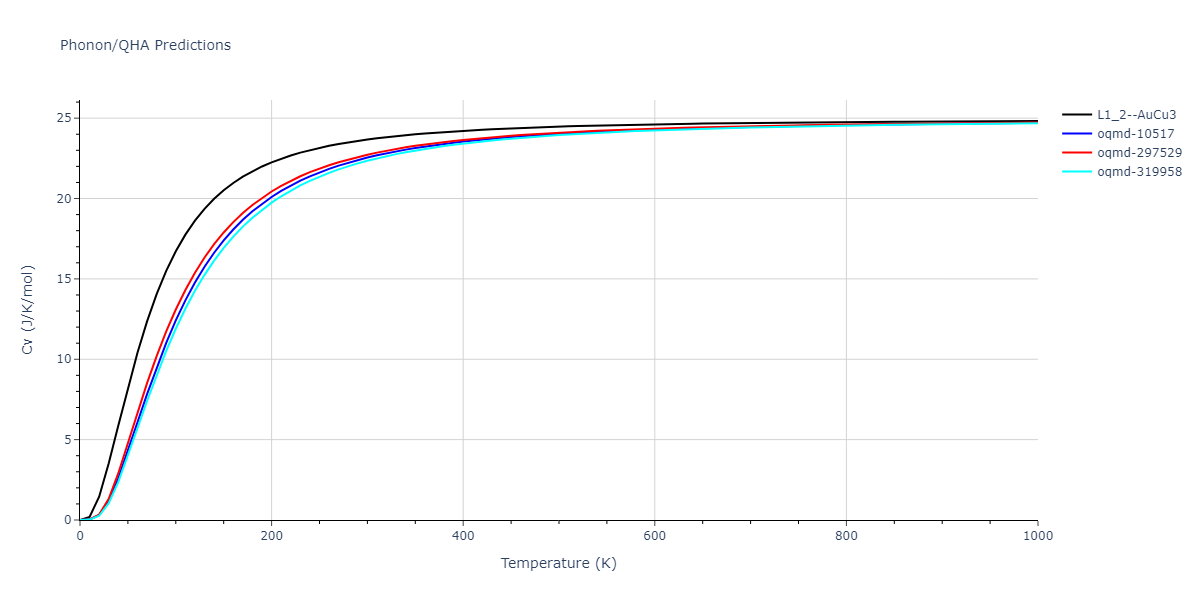
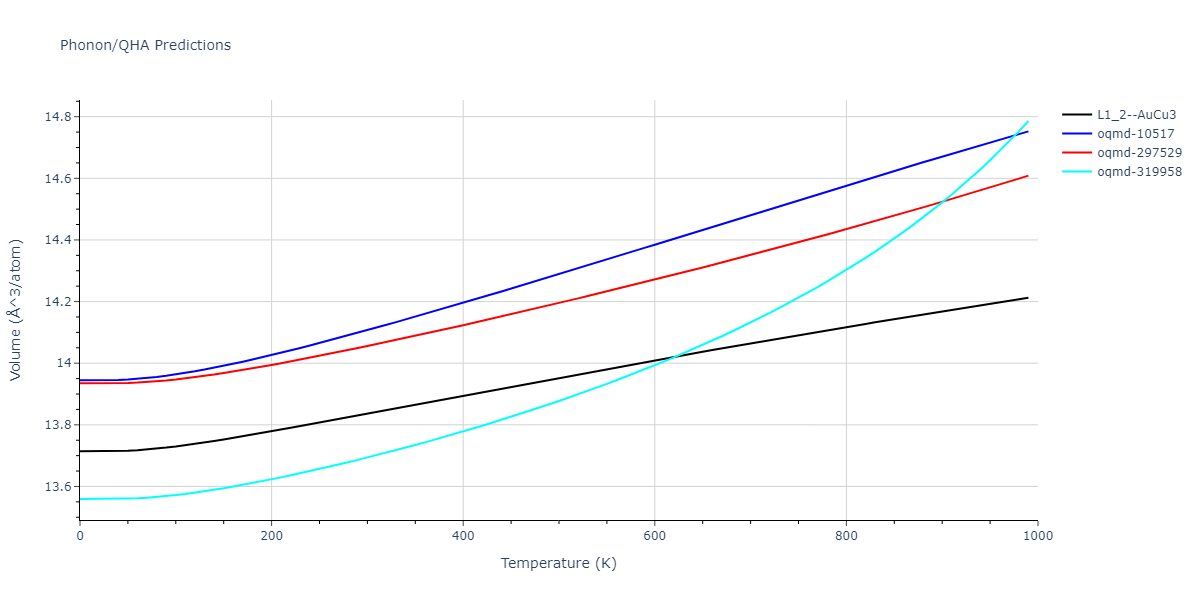
| L1_2--AuCu3 | static | -2.9276 | -2.9276 | 3.9248 | 3.9248 | 3.9248 | 90.0 | 90.0 | 90.0 |
| D0_3--BiF3 | static | -2.9229 | -2.9229 | 6.0748 | 6.0748 | 6.0748 | 90.0 | 90.0 | 90.0 |
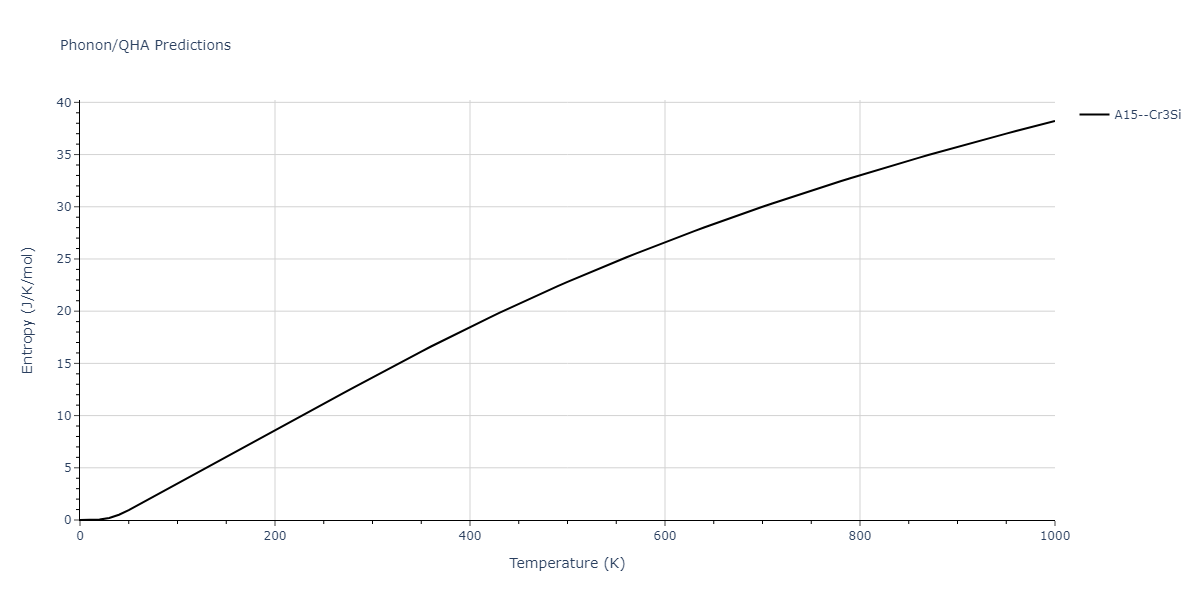
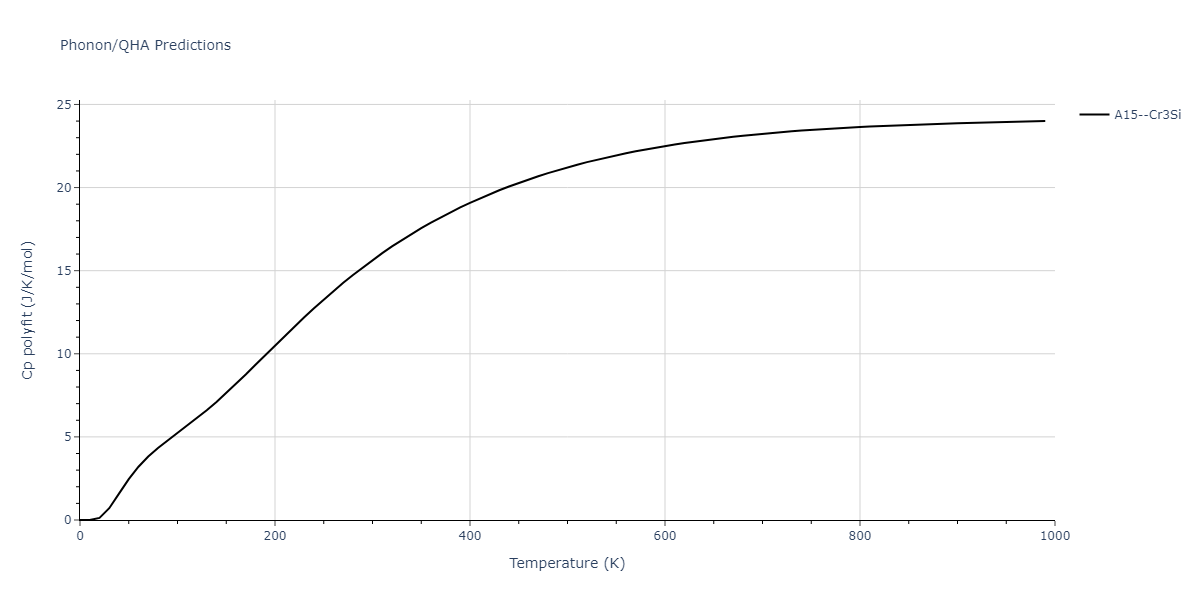
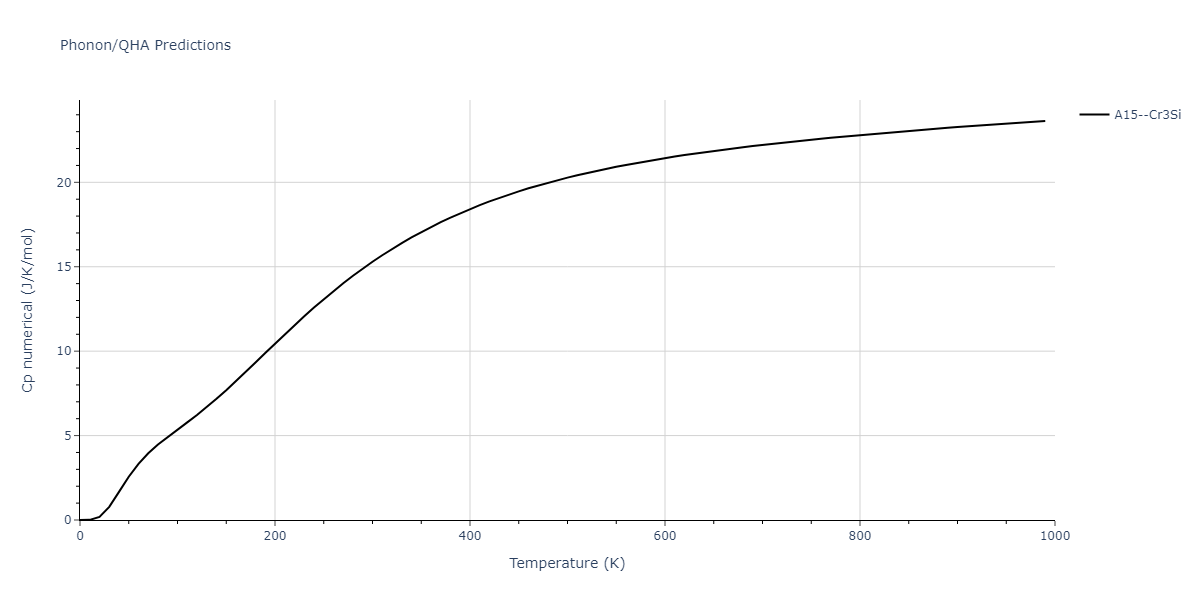
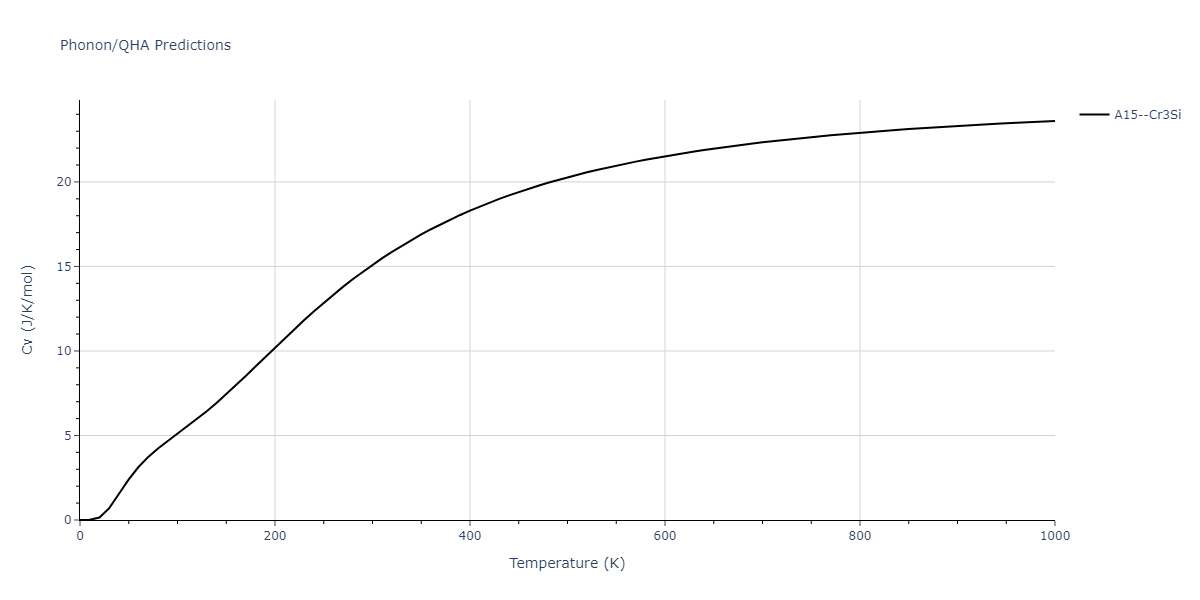
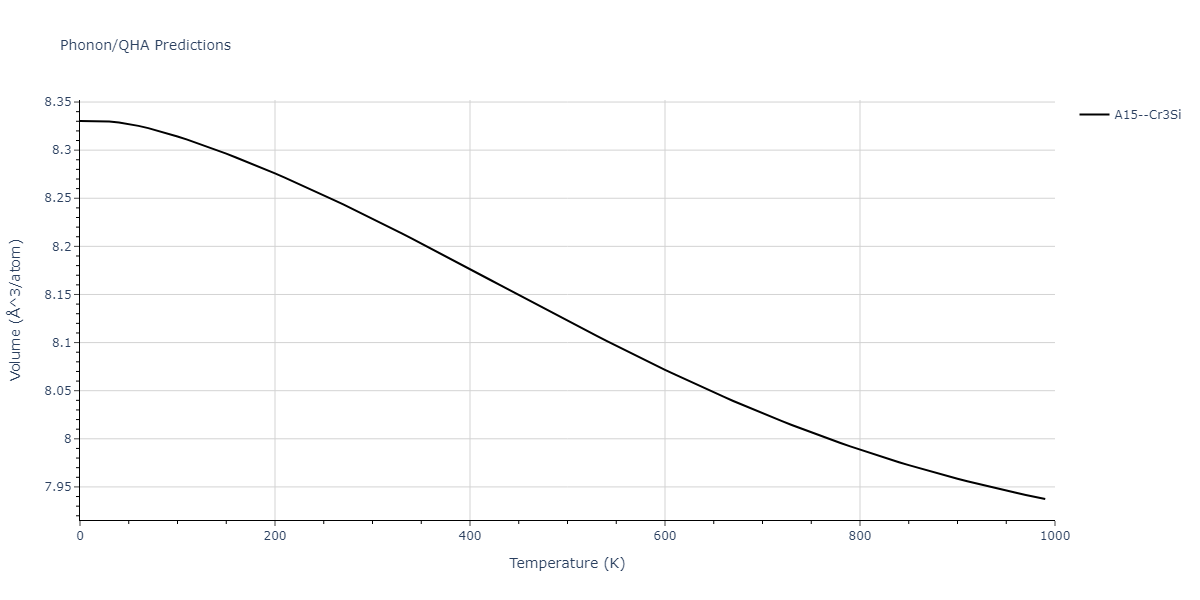
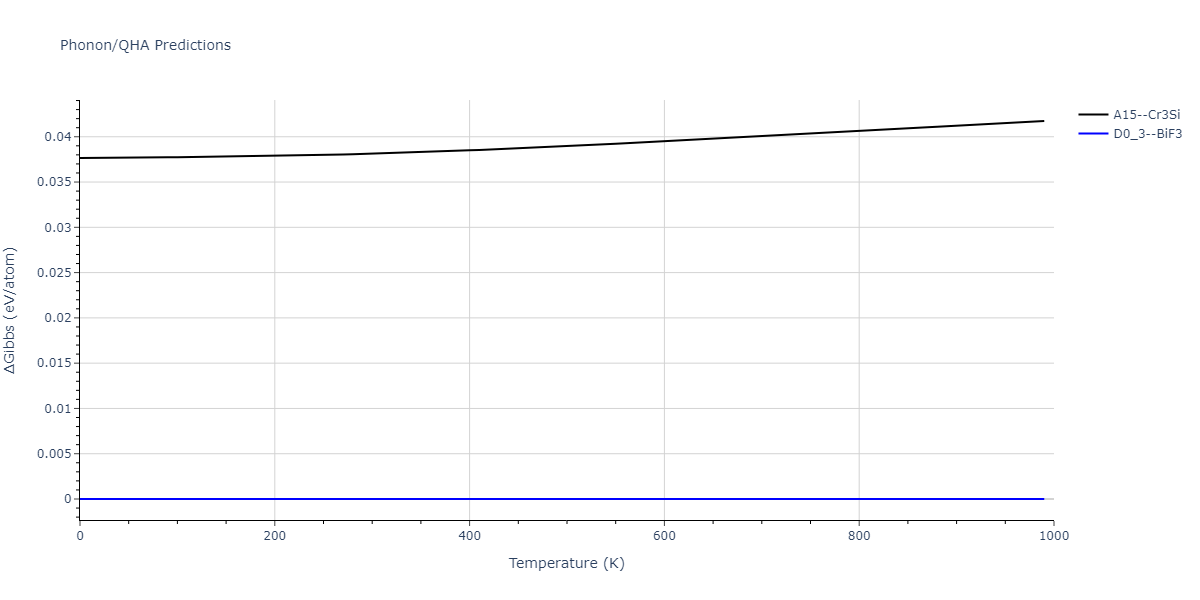
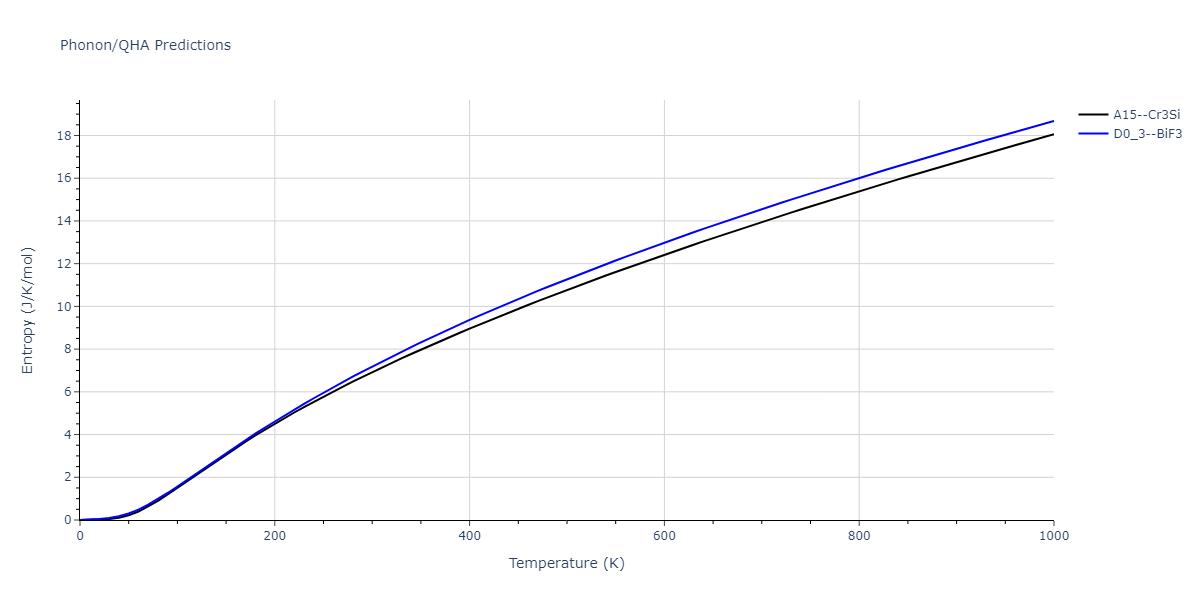
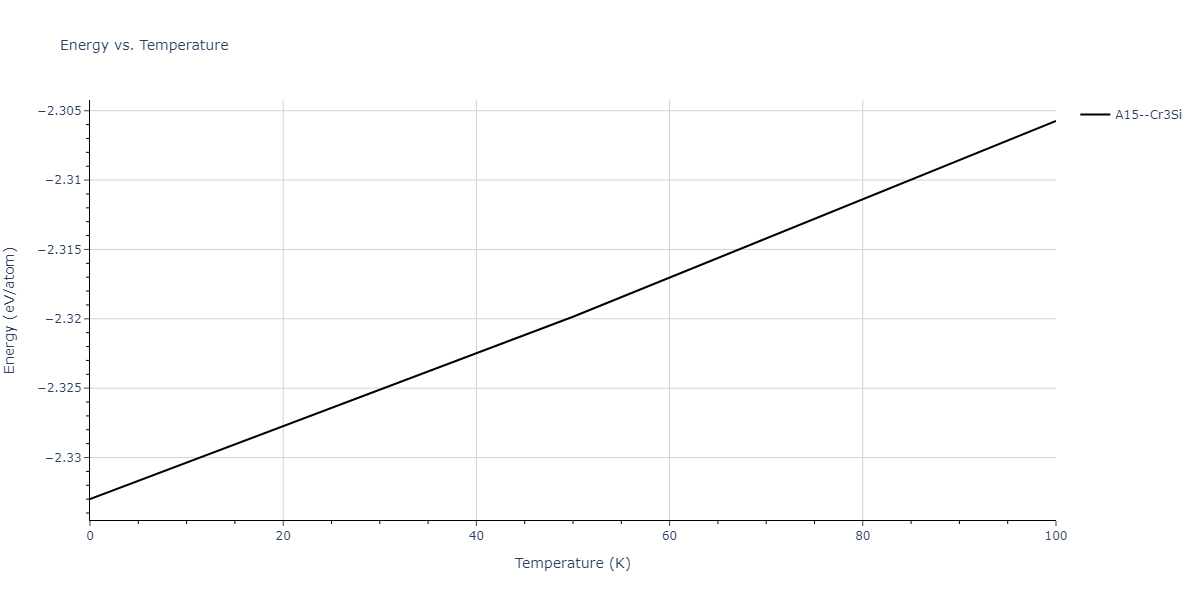
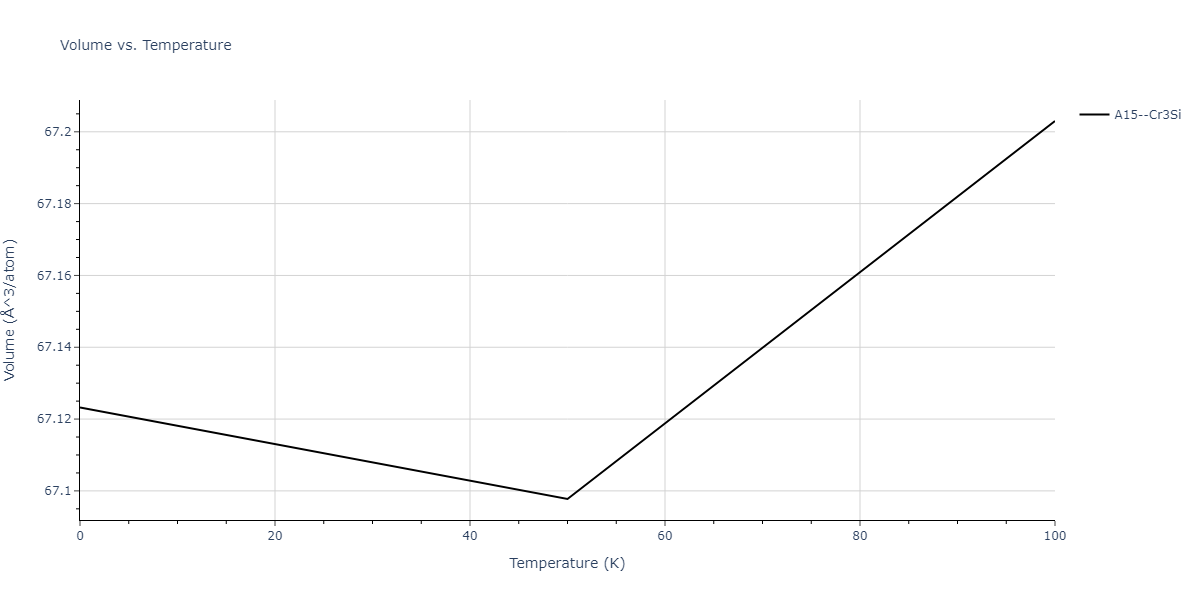
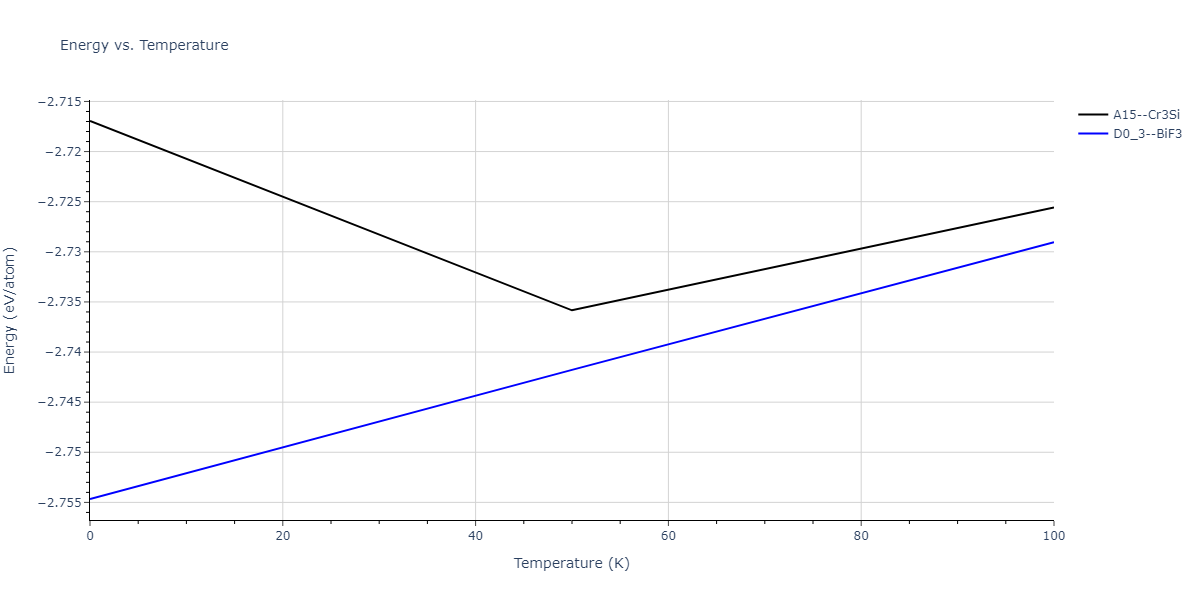
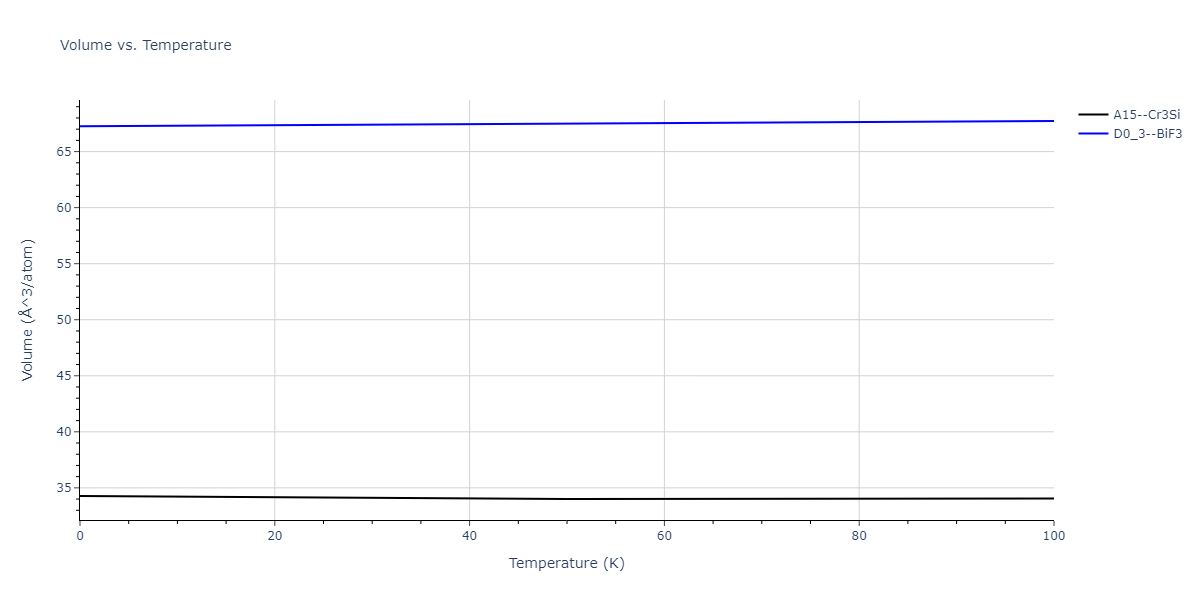
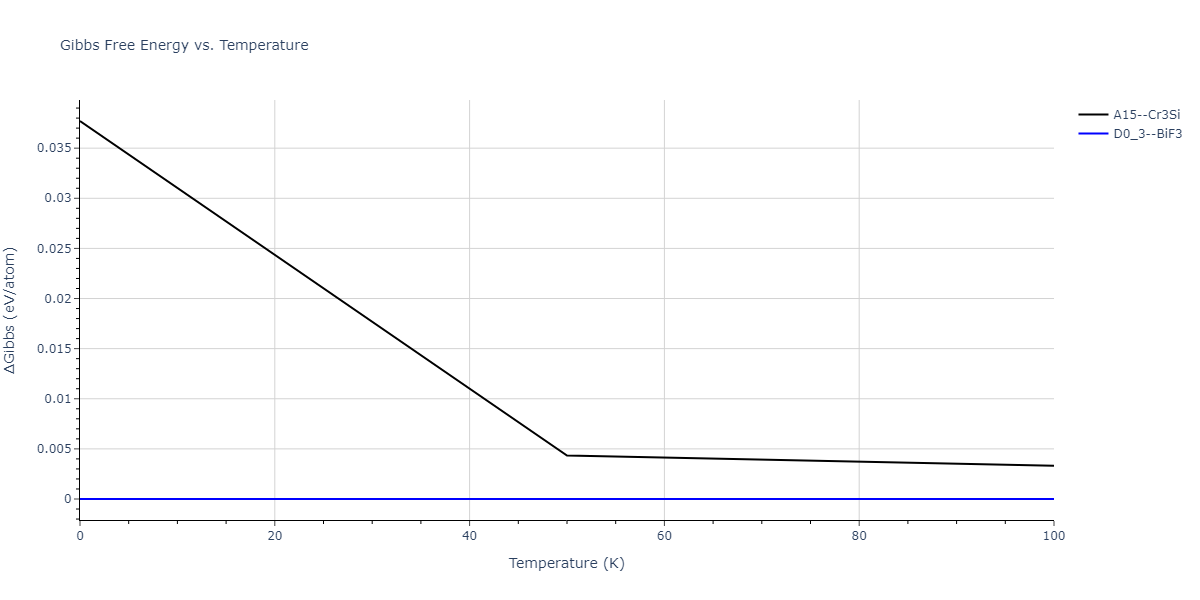
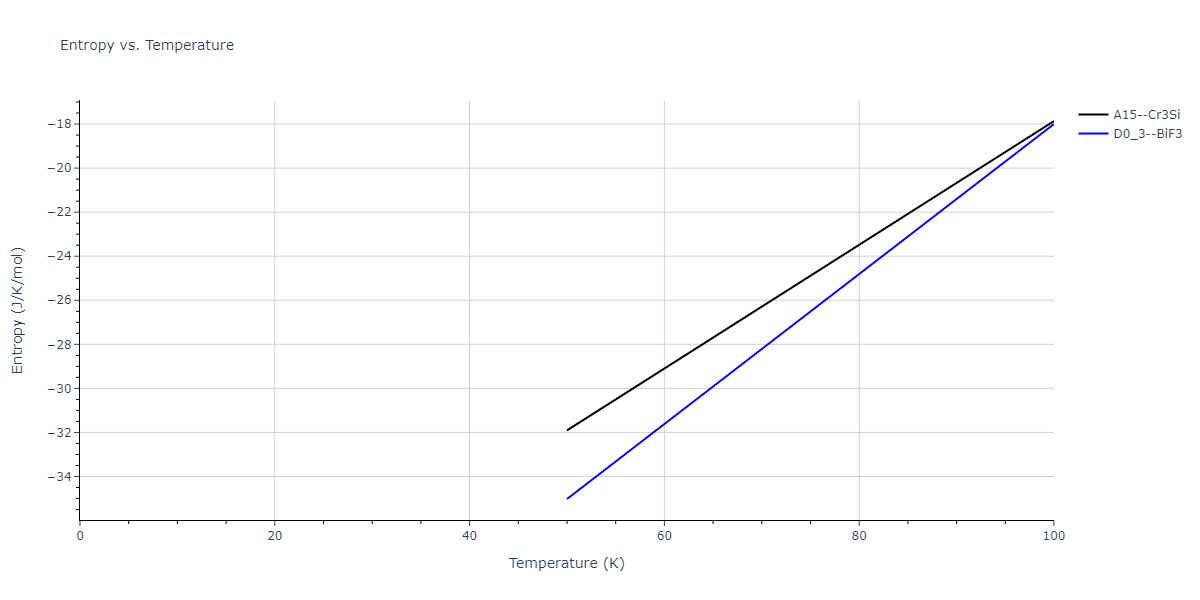
| A15--Cr3Si | static | -2.8829 | -2.8829 | 4.9463 | 4.9463 | 4.9463 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
D0_3--BiF3 = oqmd-308055
L1_2--AuCu3 = oqmd-344444
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
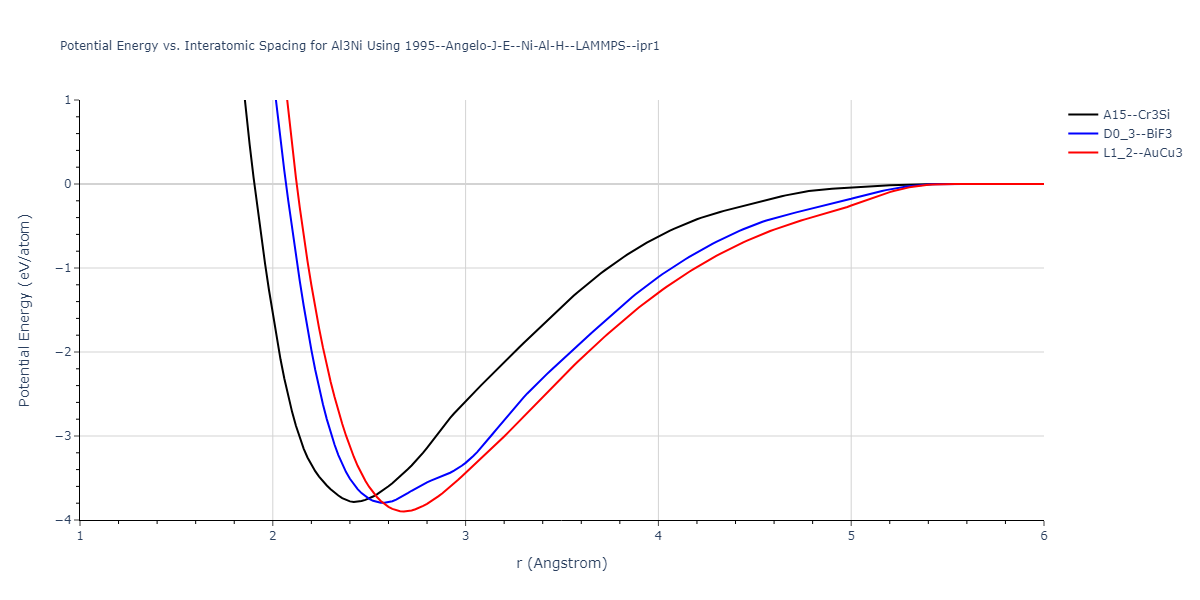
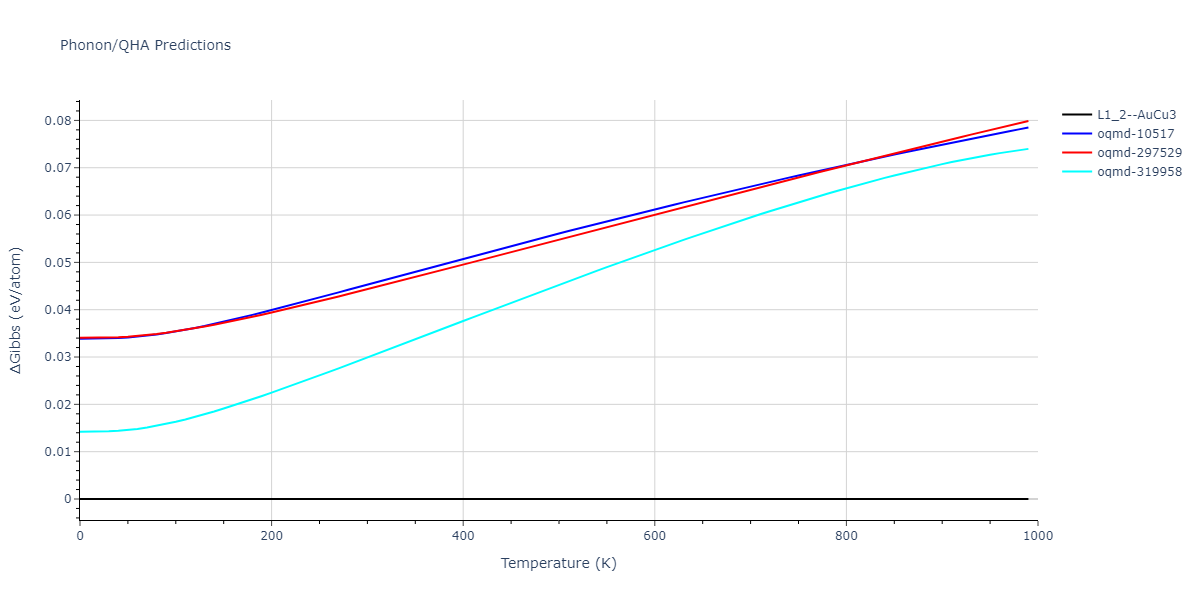
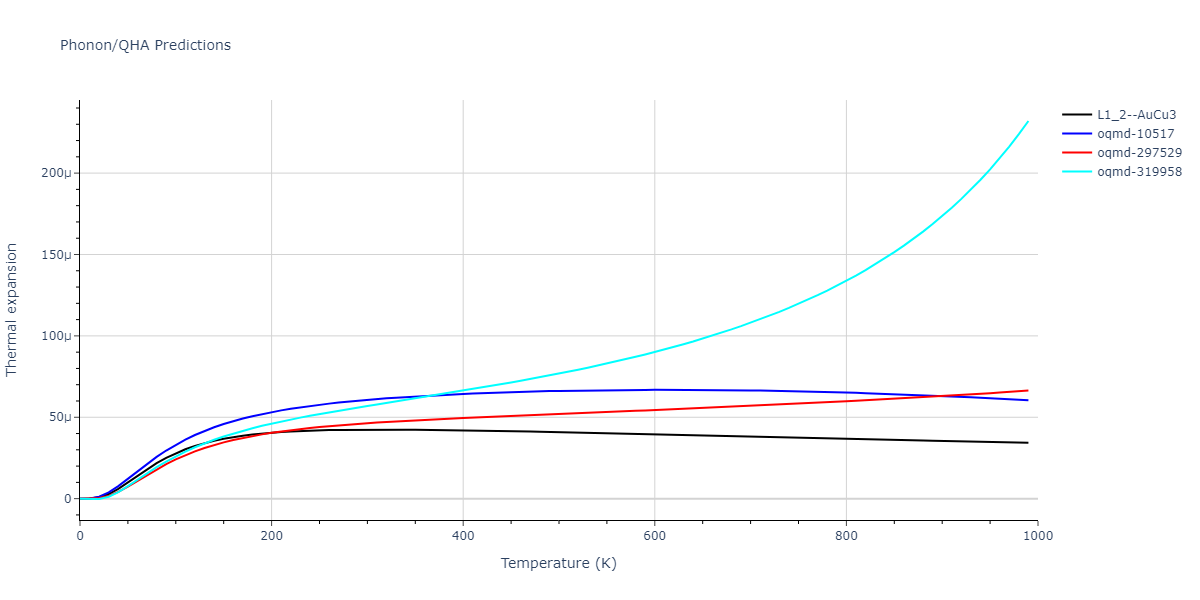
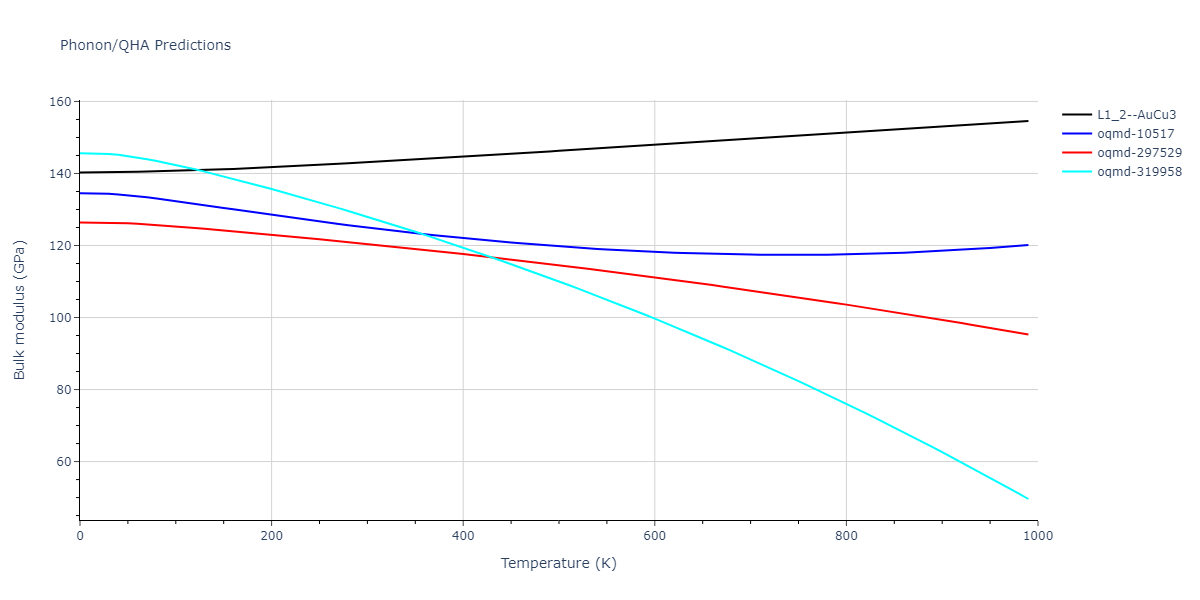
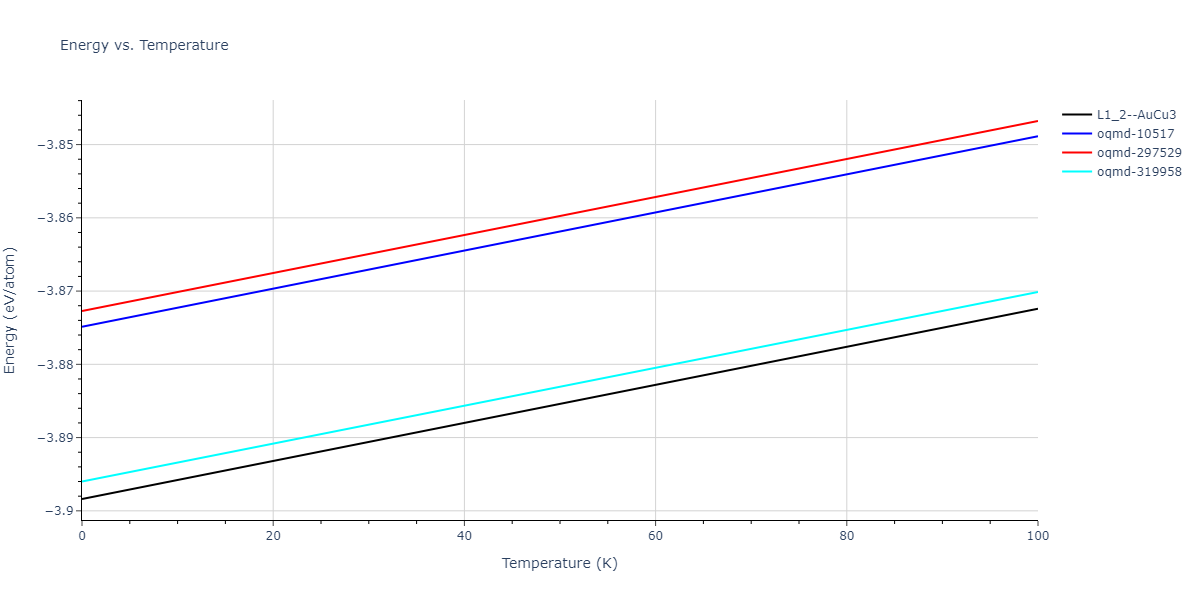
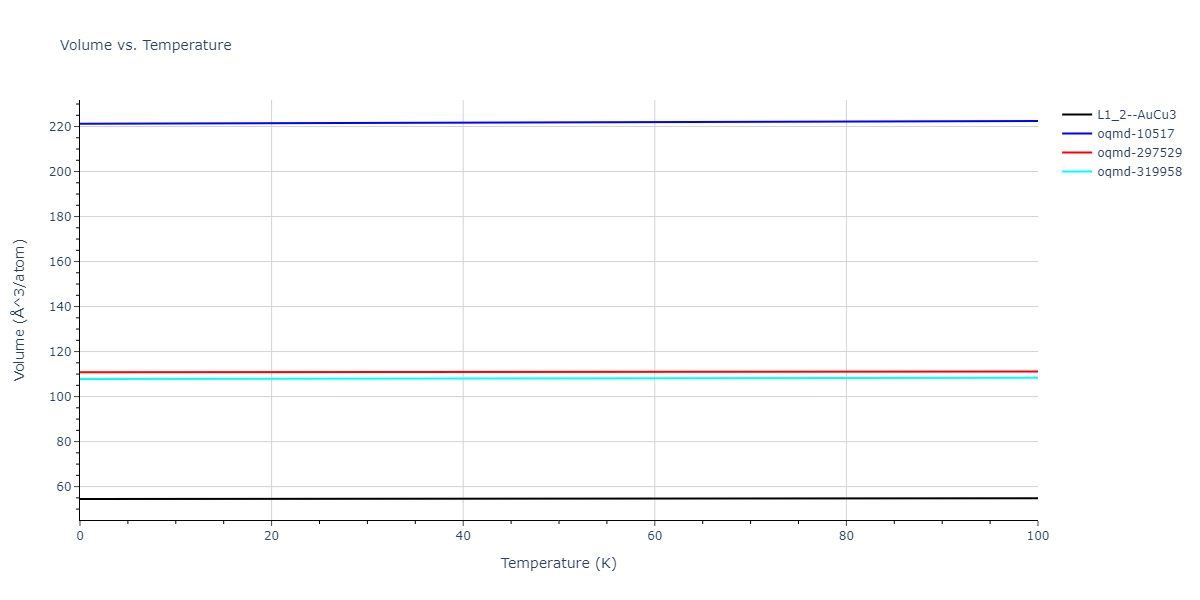
| L1_2--AuCu3 | dynamic | -3.8984 | -3.8984 | 3.7912 | 3.7912 | 3.7912 | 90.0 | 90.0 | 90.0 |
| oqmd-319958 | dynamic | -3.896 | -3.896 | 5.4478 | 5.4478 | 4.1967 | 90.0 | 90.0 | 120.0 |
| oqmd-319958 | box | -3.8928 | -3.8928 | 5.421 | 5.421 | 4.2176 | 90.0 | 90.0 | 120.0 |
| oqmd-10517 | dynamic | -3.8749 | -3.8749 | 4.8272 | 8.4665 | 5.4144 | 90.0 | 90.0 | 90.0 |
| oqmd-297529 | dynamic | -3.8727 | -3.8727 | 3.7547 | 3.7547 | 7.8606 | 90.0 | 90.0 | 90.0 |
| oqmd-10517 | box | -3.8193 | -3.8193 | 6.5155 | 7.7361 | 4.7993 | 90.0 | 90.0 | 90.0 |
| mp-622209 | box | -3.8159 | -3.8159 | 6.5468 | 7.7182 | 4.7901 | 90.0 | 90.0 | 90.0 |
| D0_3--BiF3 | static | -3.7961 | -3.7961 | 5.9412 | 5.9412 | 5.9412 | 90.0 | 90.0 | 90.0 |
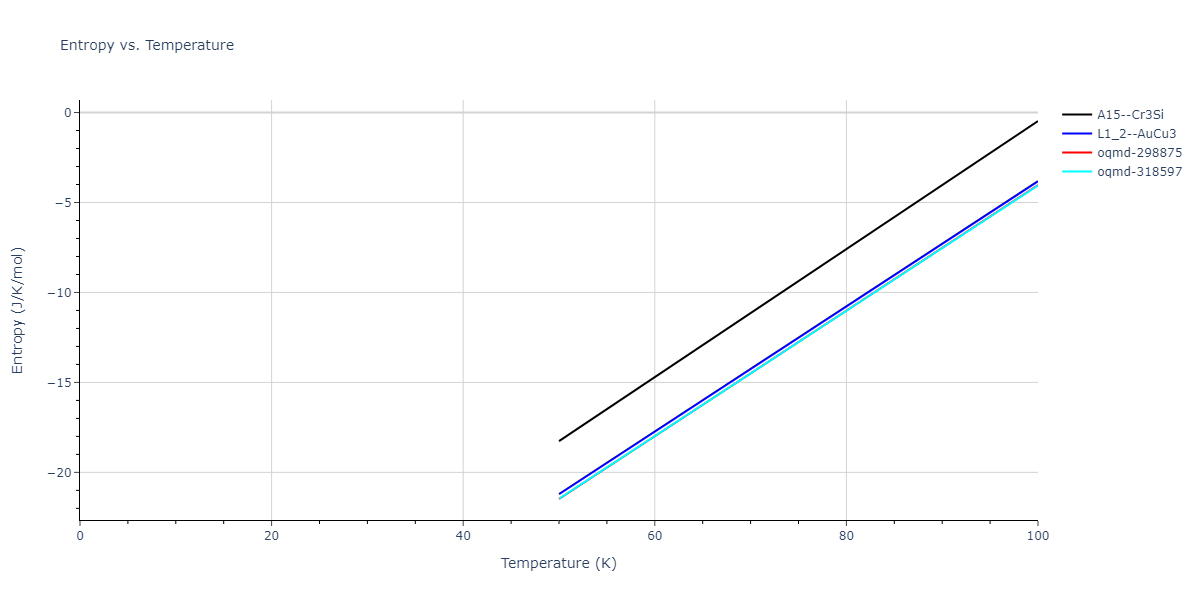
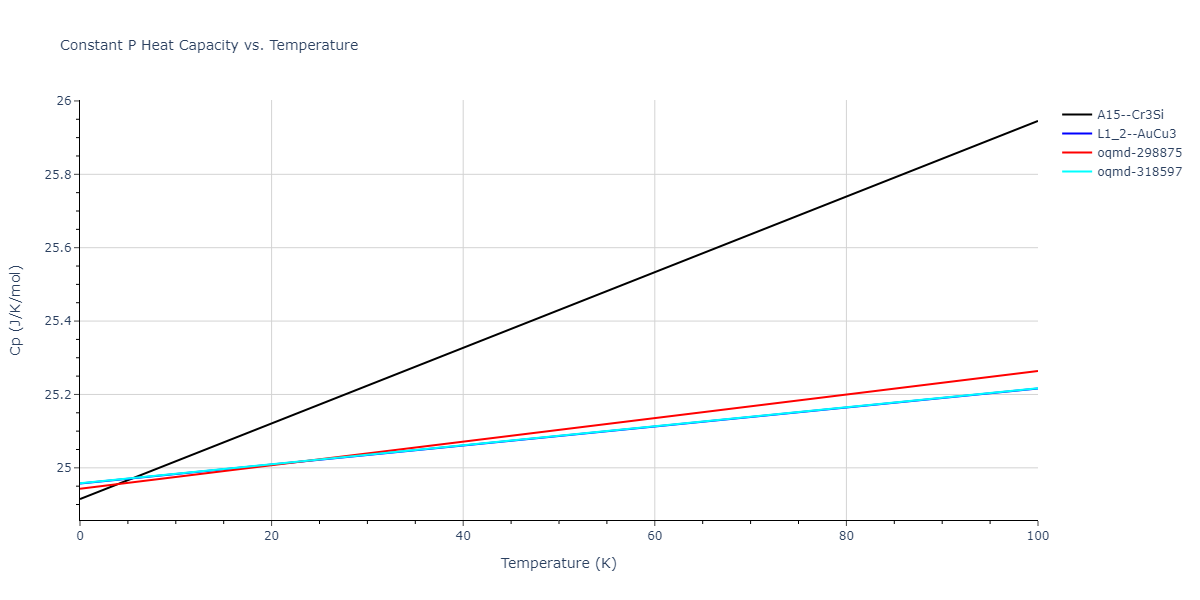
| A15--Cr3Si | static | -3.7847 | -3.7847 | 4.8479 | 4.8479 | 4.8479 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
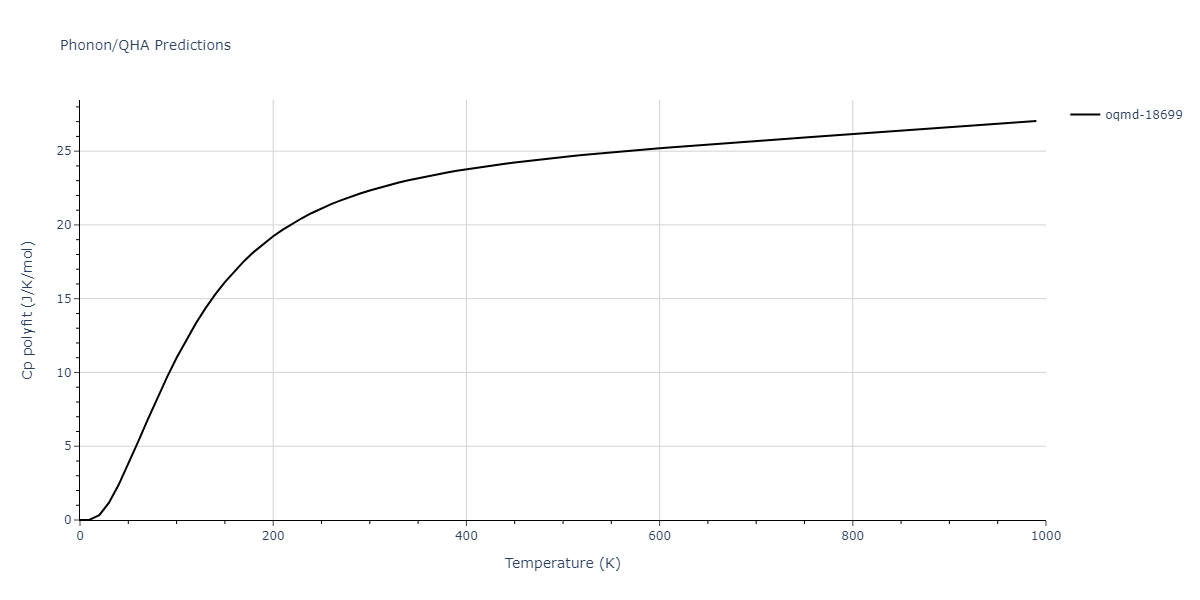
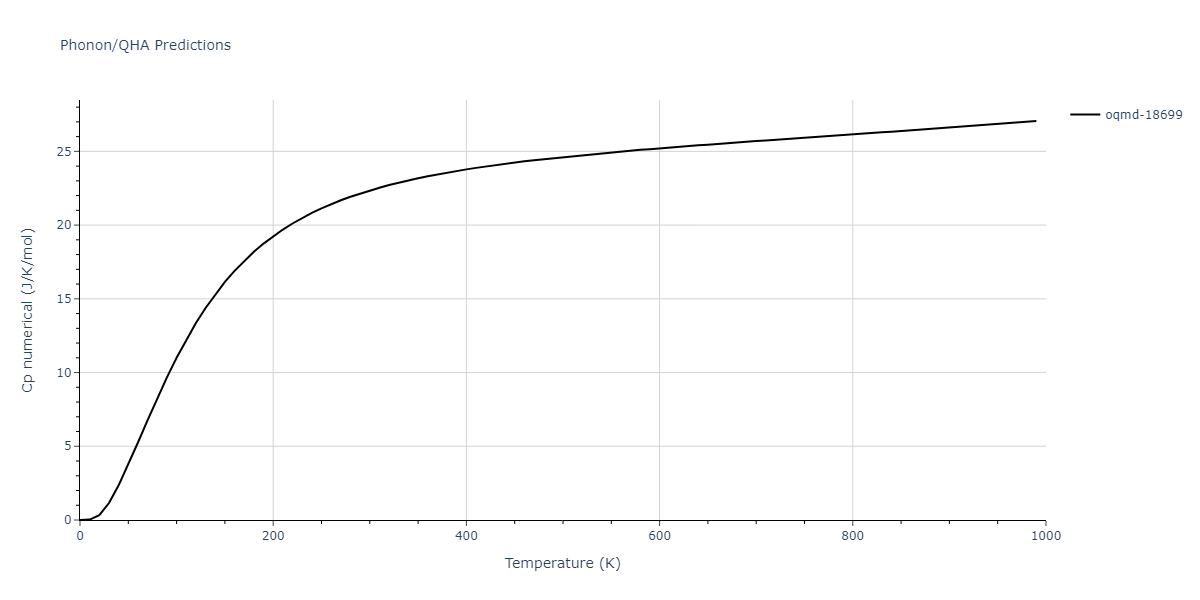
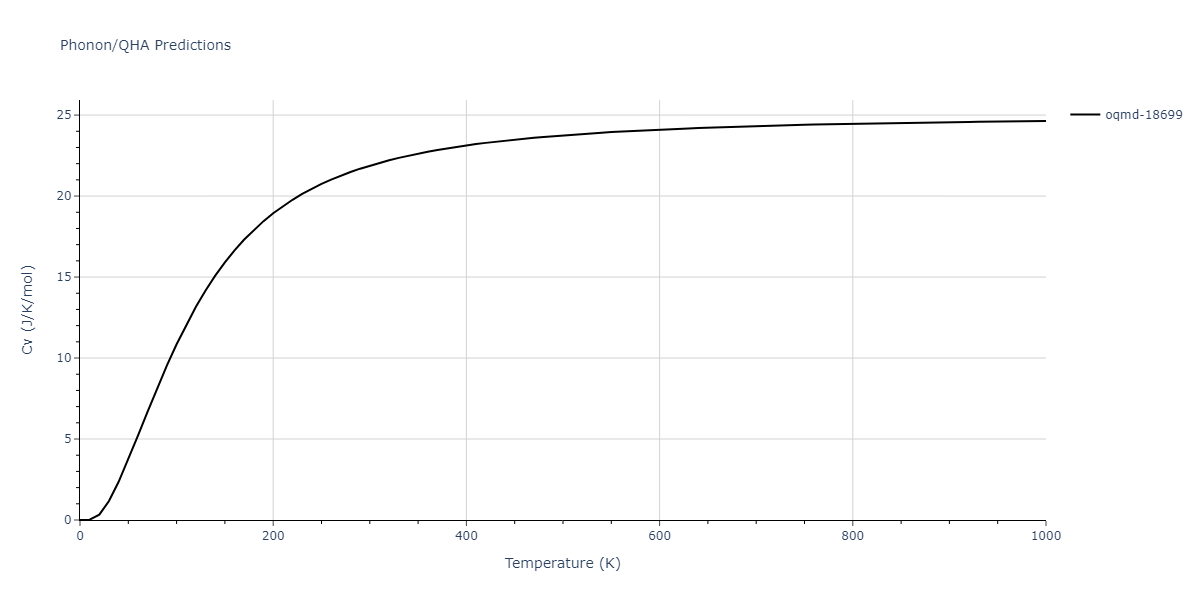
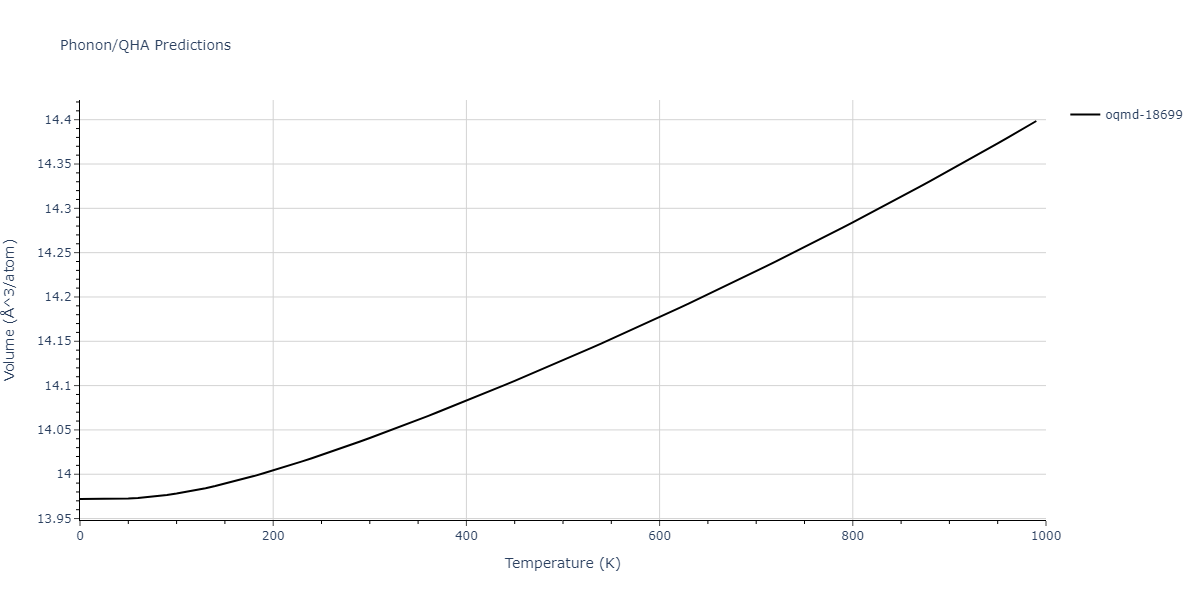
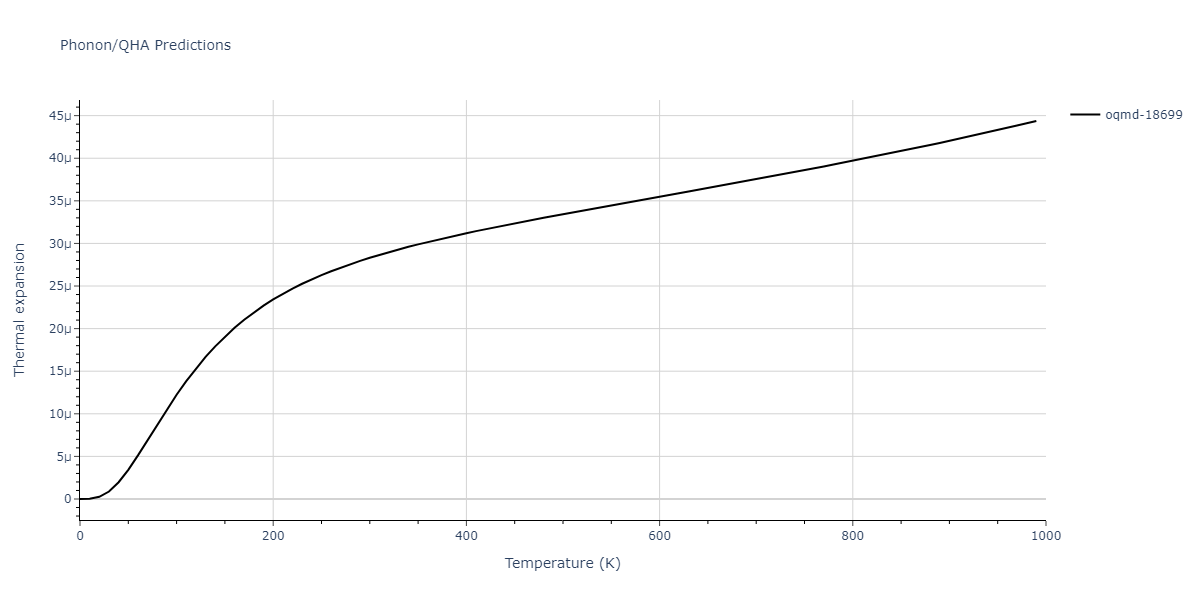
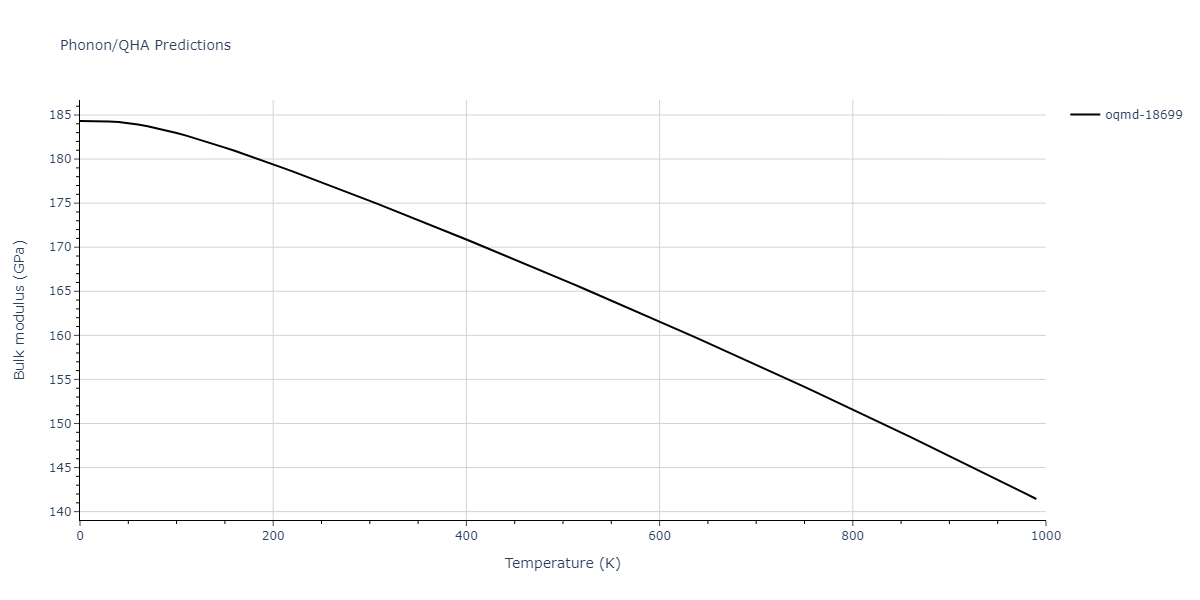
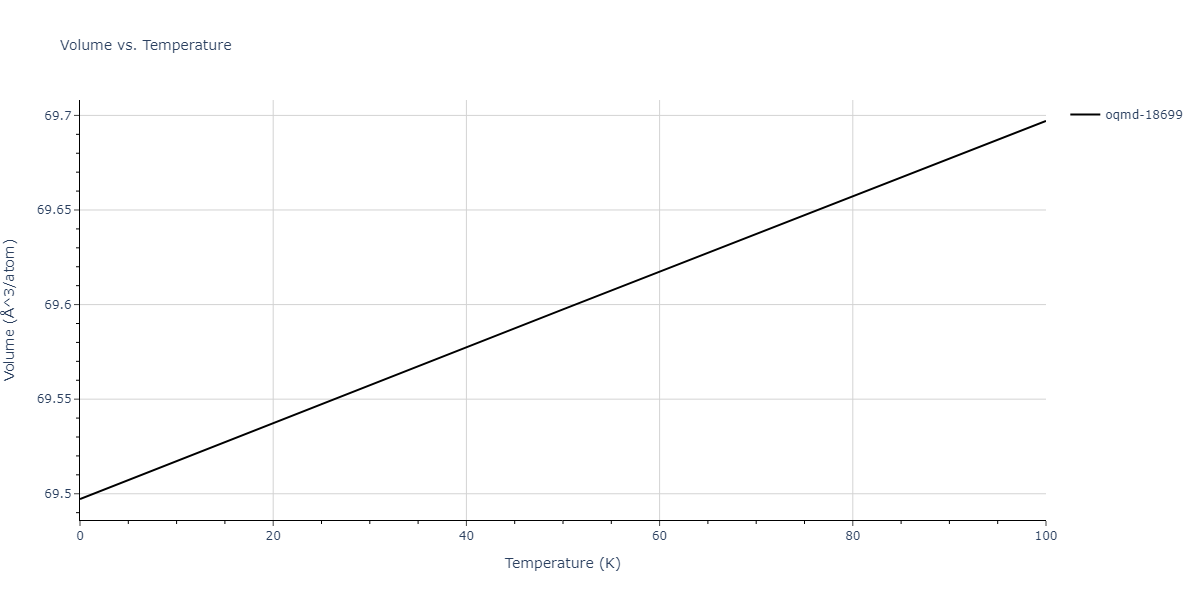
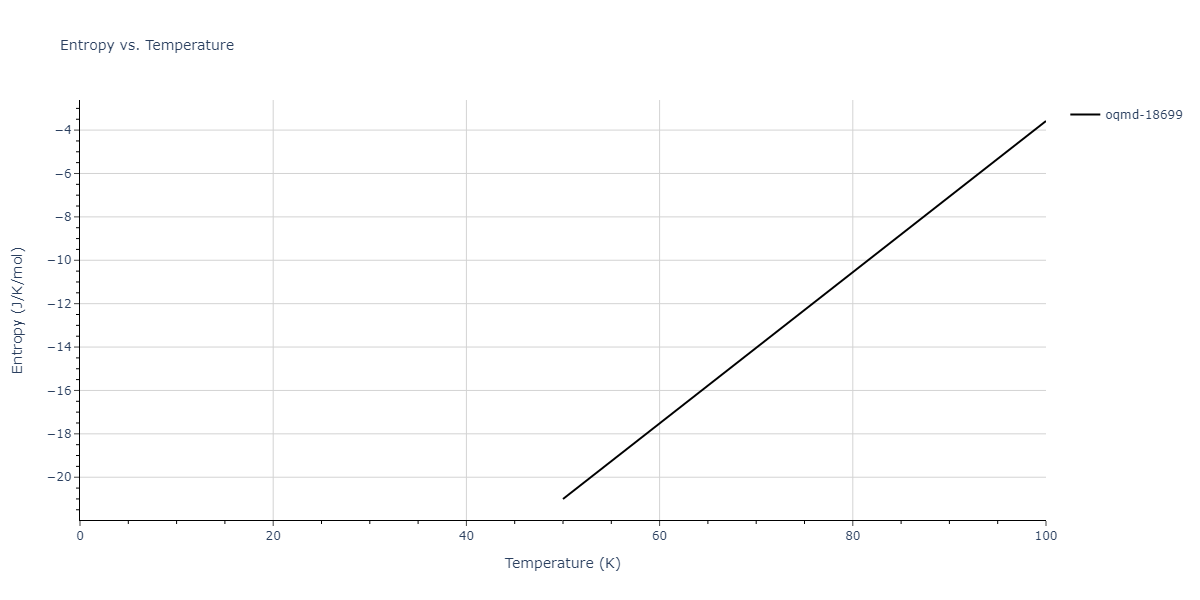
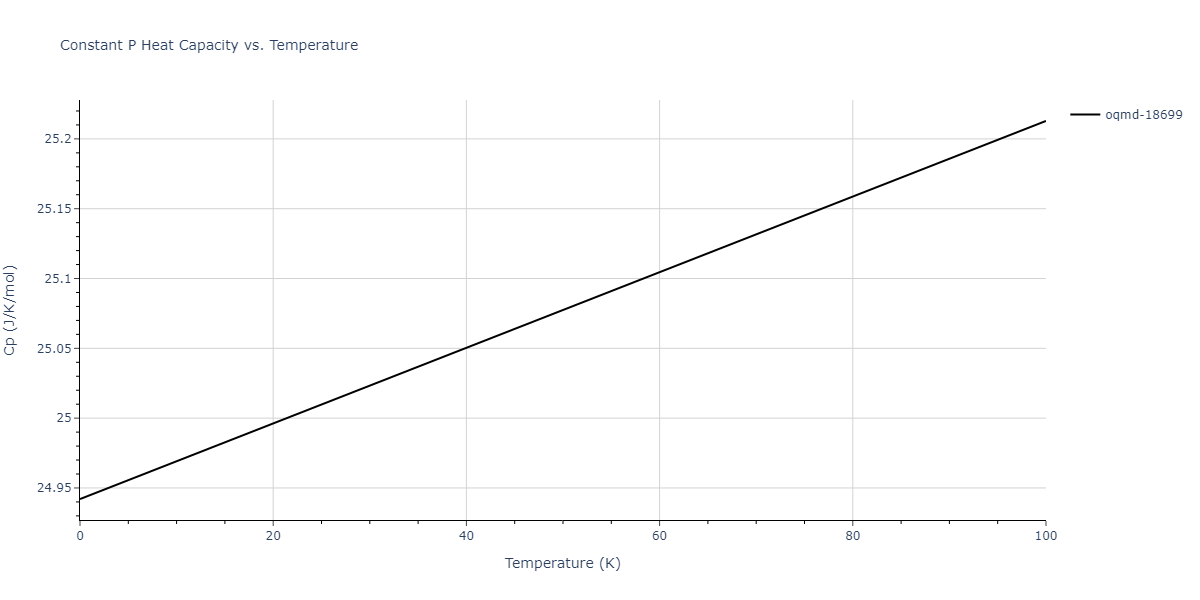
| oqmd-18699 | dynamic | -4.1349 | -4.1349 | 4.0127 | 4.0127 | 4.9837 | 90.0 | 90.0 | 120.0 |
| oqmd-18699 | box | -4.1331 | -4.1331 | 4.0181 | 4.0181 | 4.9781 | 90.0 | 90.0 | 120.0 |
| mp-1057 | box | -4.1321 | -4.1321 | 4.0193 | 4.0193 | 4.9778 | 90.0 | 90.0 | 120.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-16514 | dynamic | -4.5108 | -4.5108 | 7.0312 | 7.3308 | 3.6541 | 90.0 | 90.0 | 90.0 |
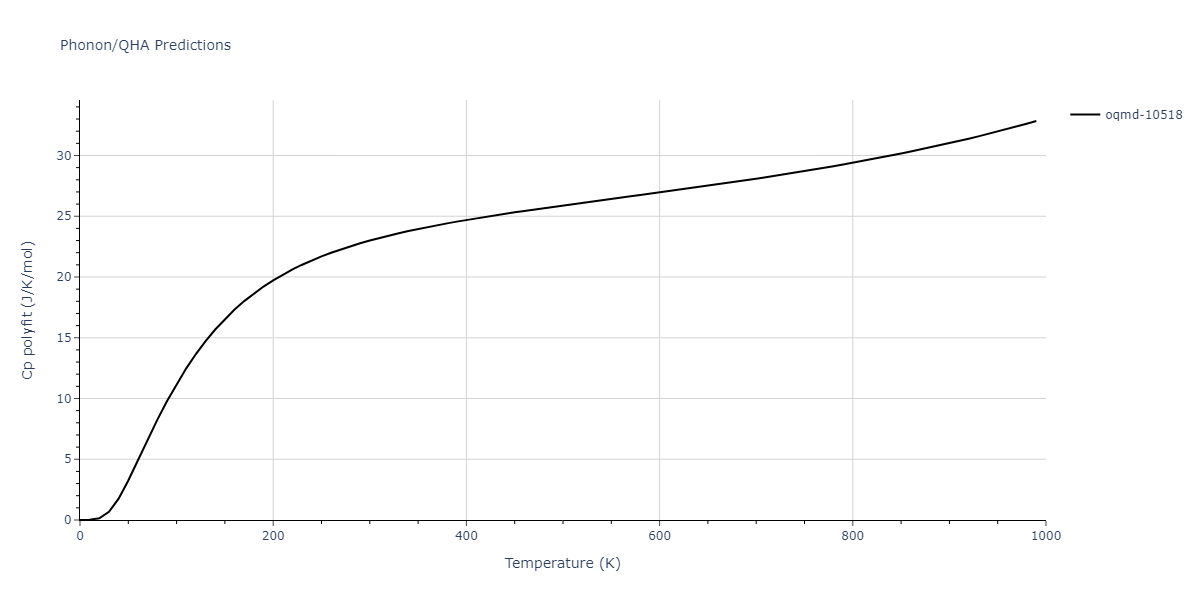
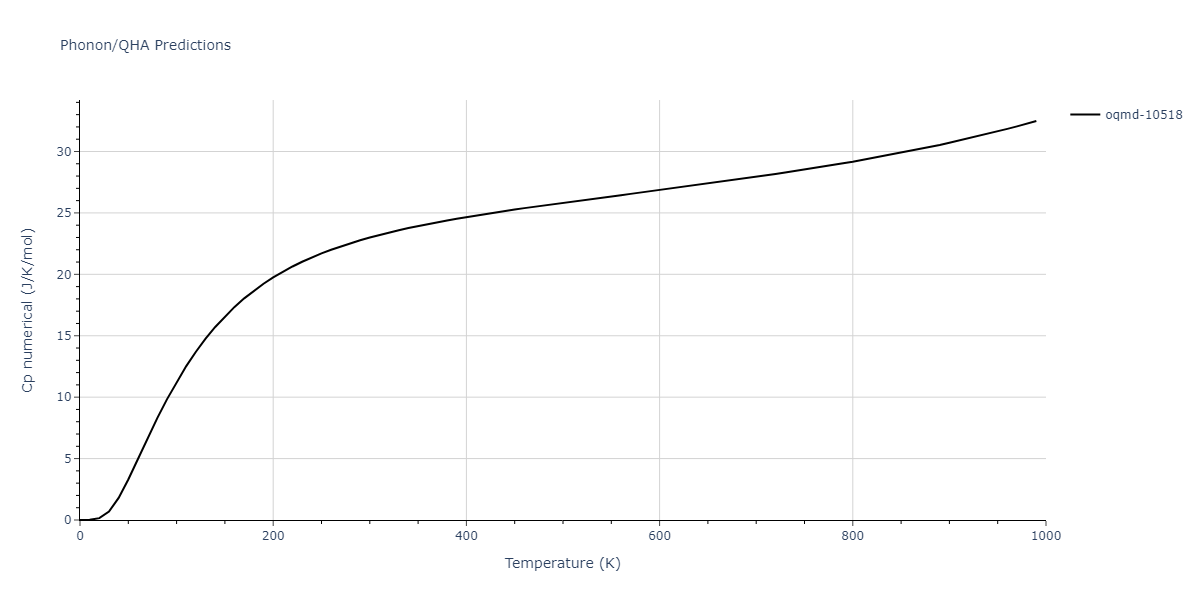
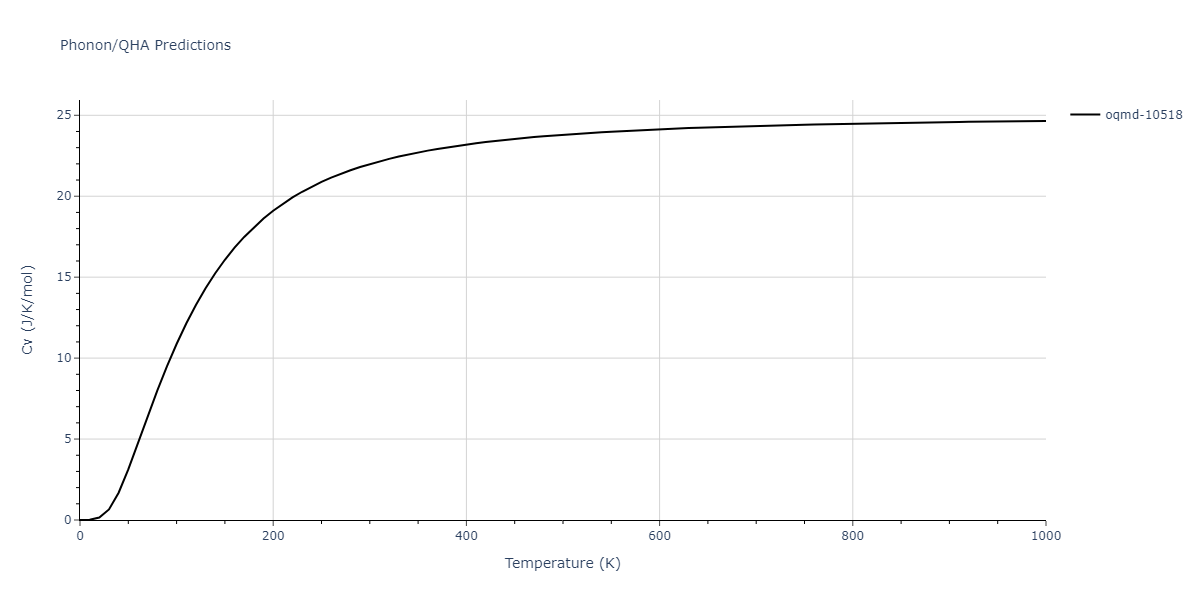
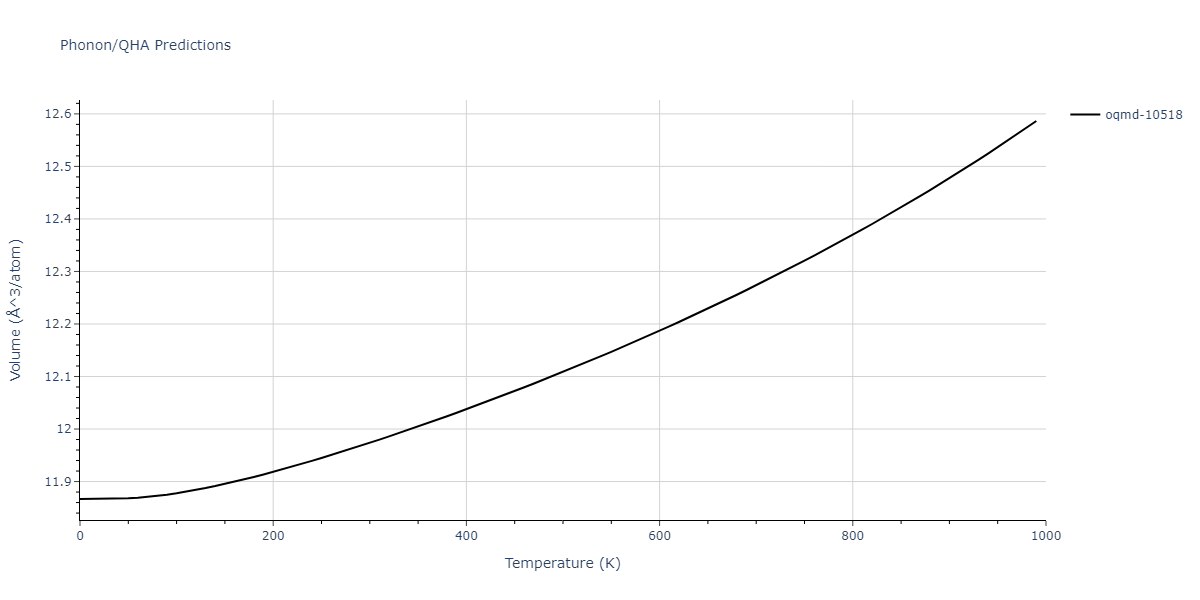
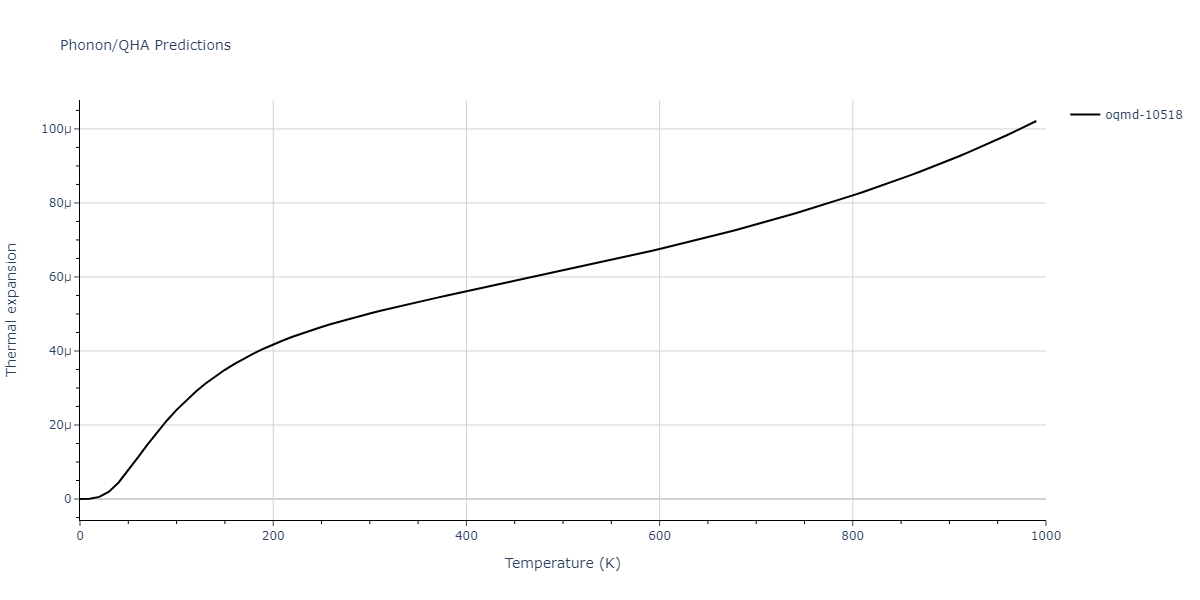
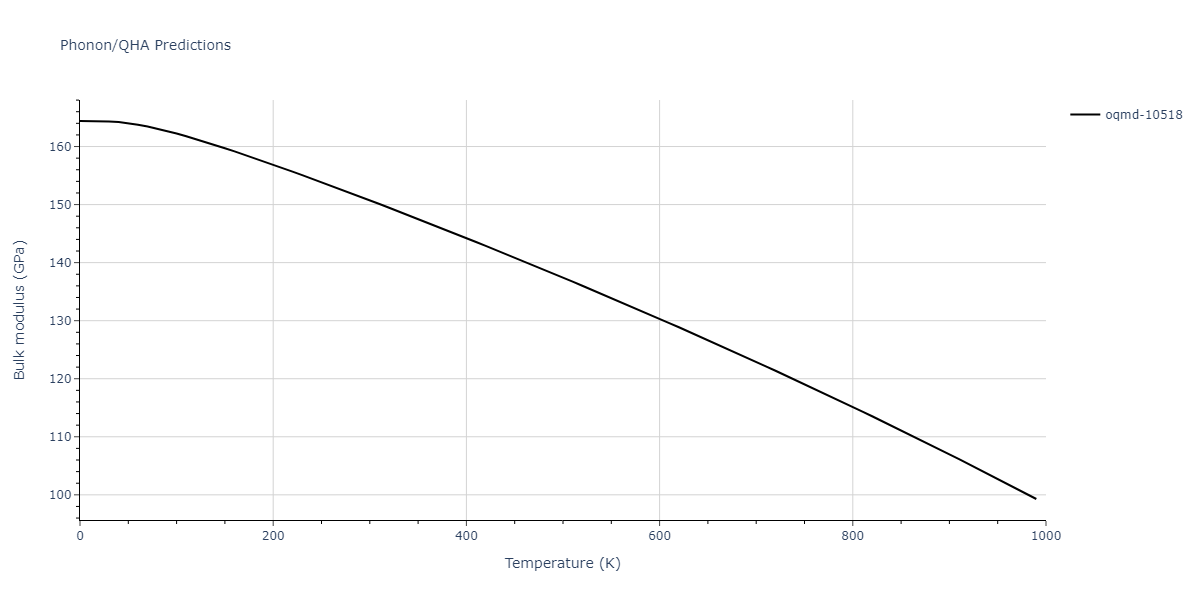
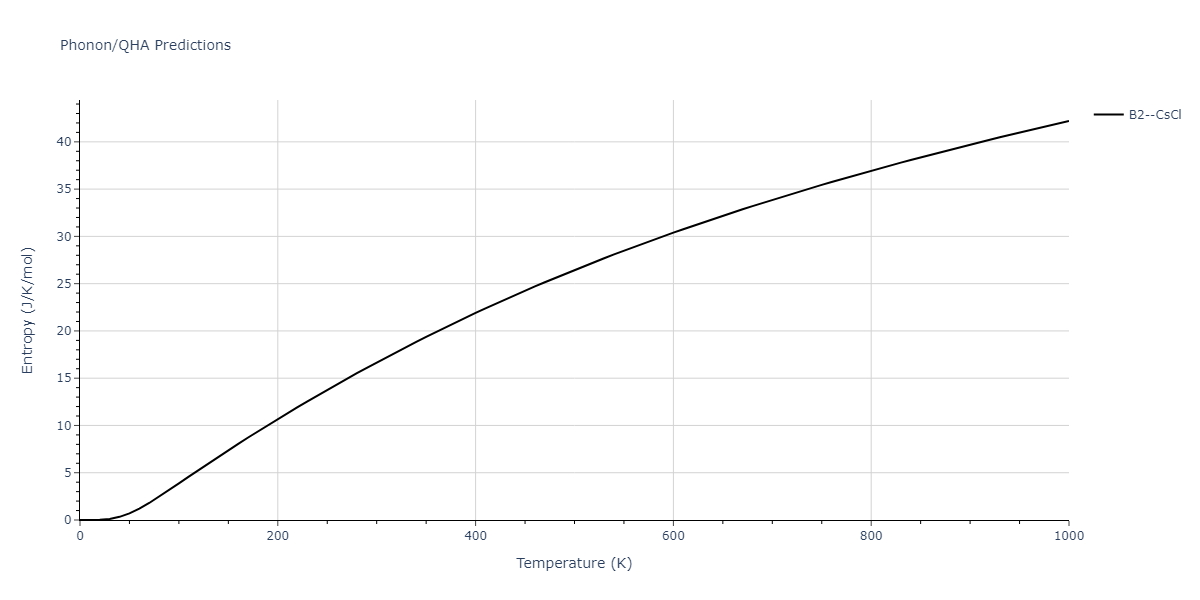
| oqmd-10518 | box | -4.4955 | -4.4955 | 6.9225 | 7.3114 | 3.738 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-1228713 | dynamic | -4.4914 | -4.4914 | 3.5686 | 3.5686 | 17.4455 | 90.0 | 90.0 | 90.0 |
| mp-1228713 | box | -4.4901 | -4.4901 | 3.5677 | 3.5677 | 17.4596 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-16515 | dynamic | -4.2349 | -4.2349 | 11.4297 | 11.4297 | 11.4297 | 90.0 | 90.0 | 90.0 |
| oqmd-10519 | box | -4.2312 | -4.2312 | 11.4383 | 11.4383 | 11.4383 | 90.0 | 90.0 | 90.0 |
| mp-16515 | box | -4.2298 | -4.2298 | 11.4402 | 11.4402 | 11.4402 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
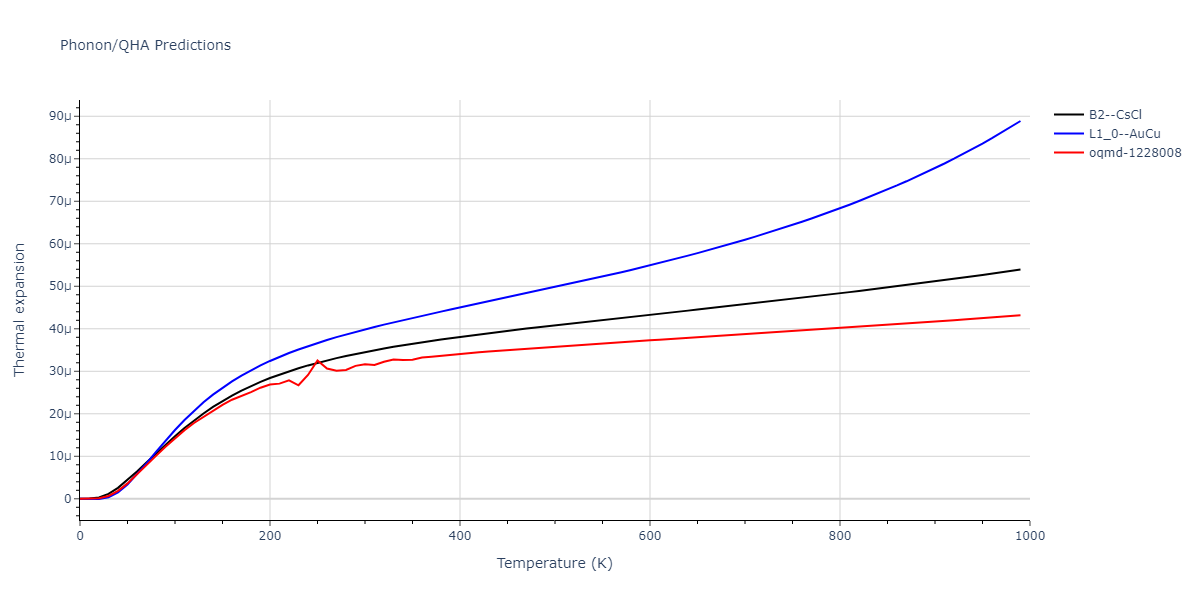
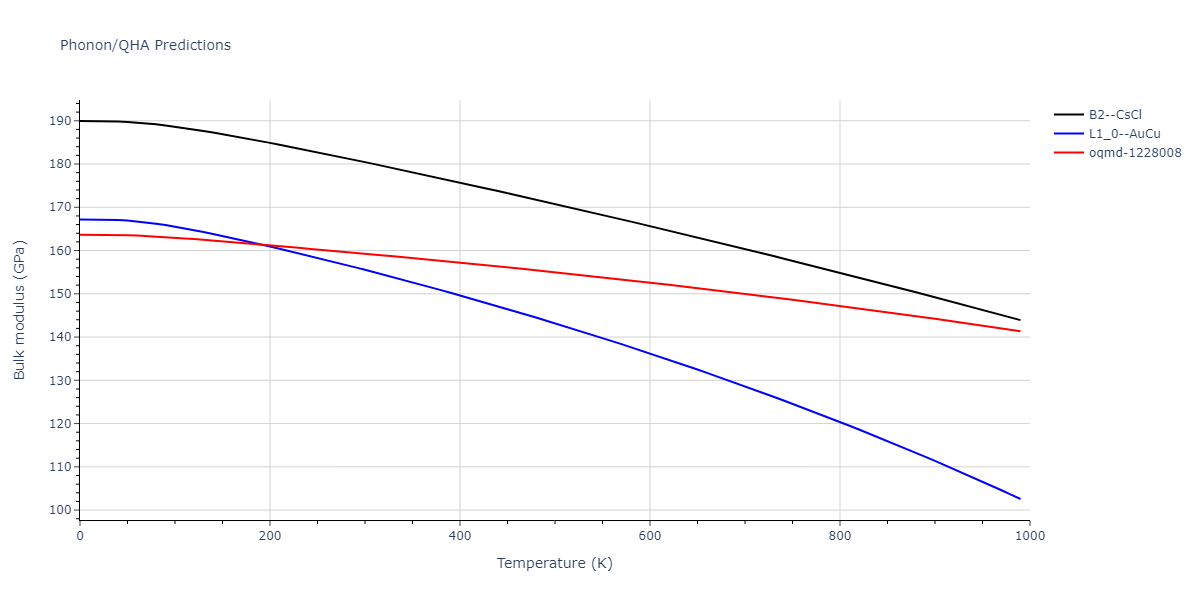
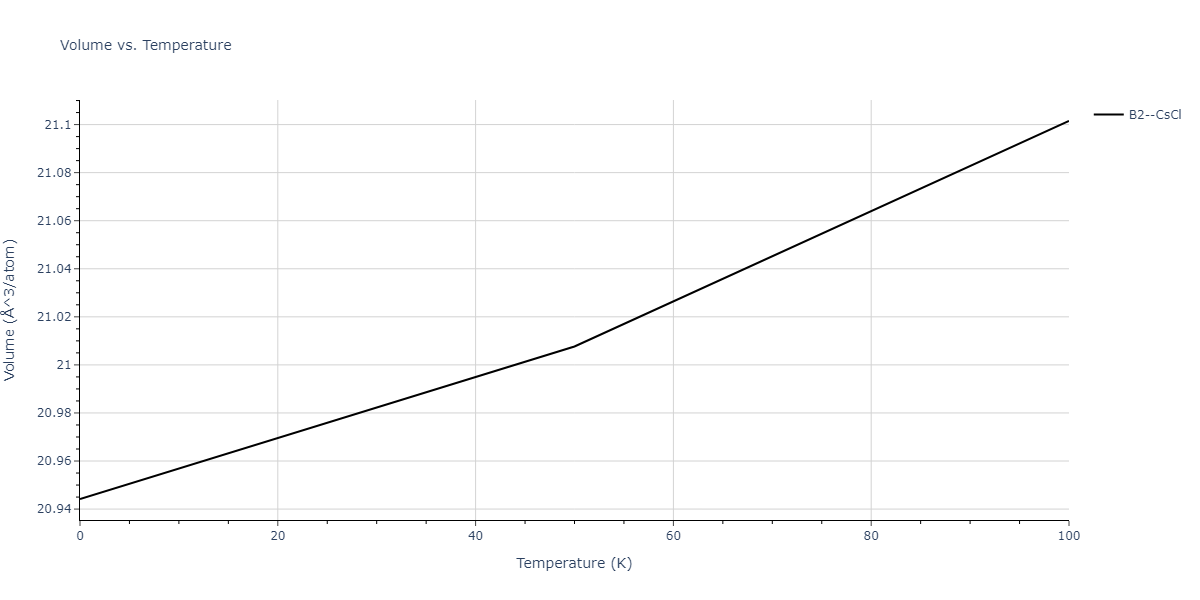
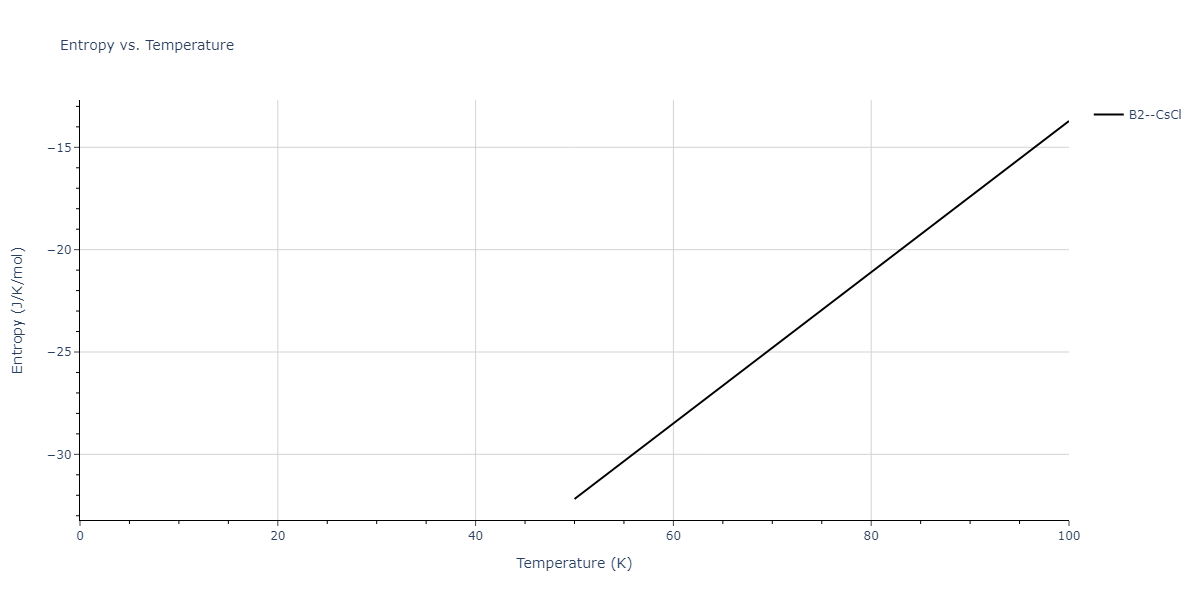
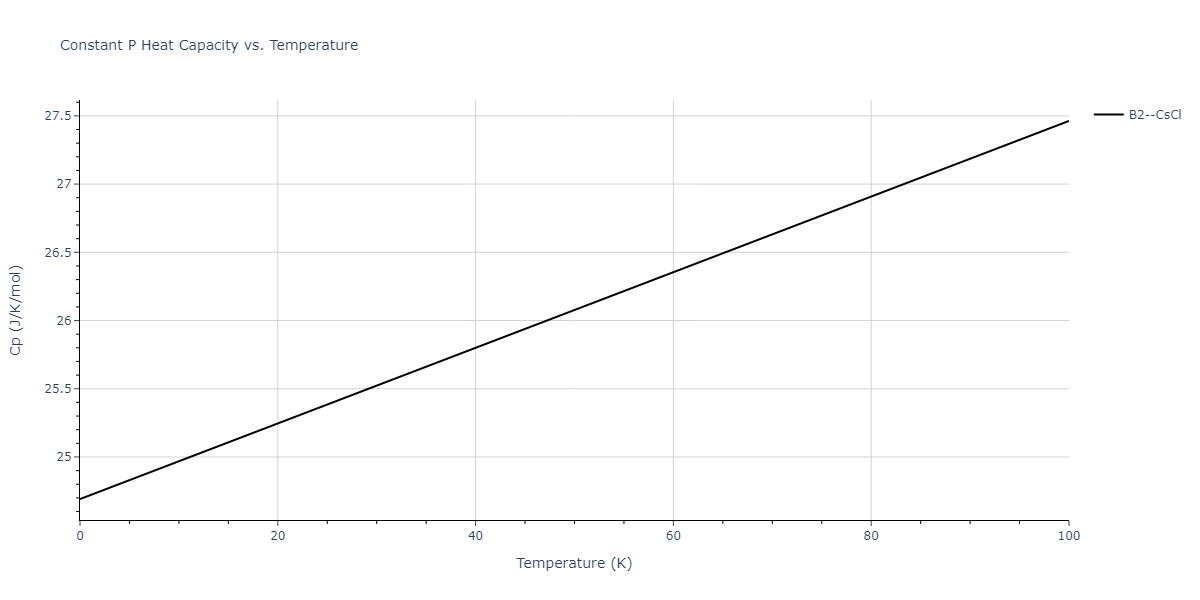
B2--CsCl = oqmd-306997
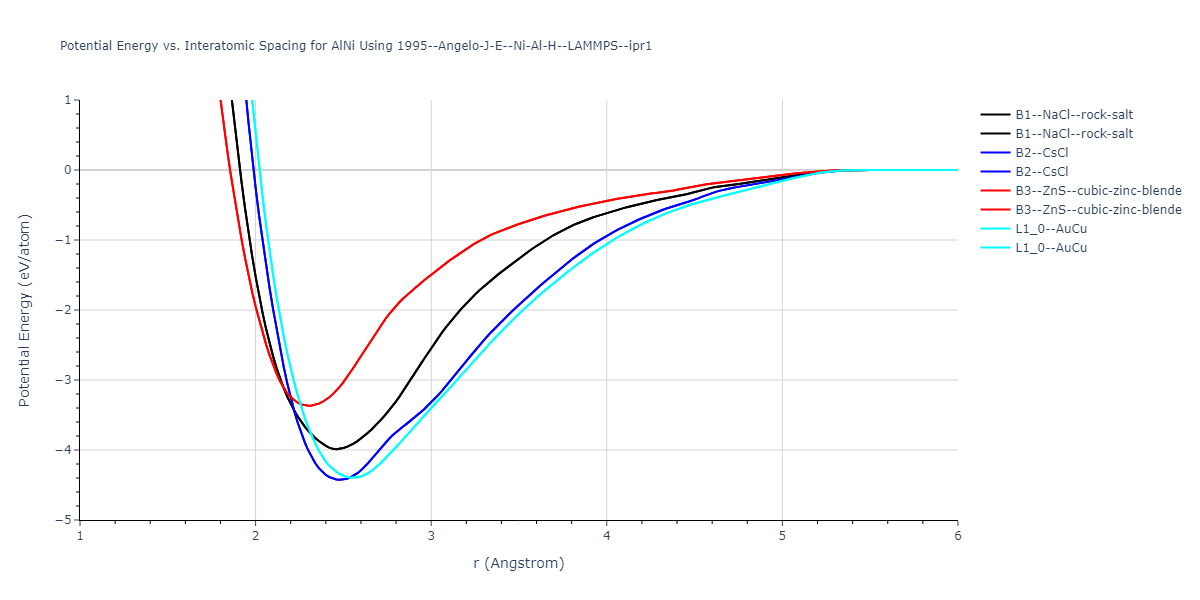
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| B2--CsCl | dynamic | -2.7571 | -2.7571 | 2.7565 | 2.7565 | 2.7565 | 90.0 | 90.0 | 90.0 |
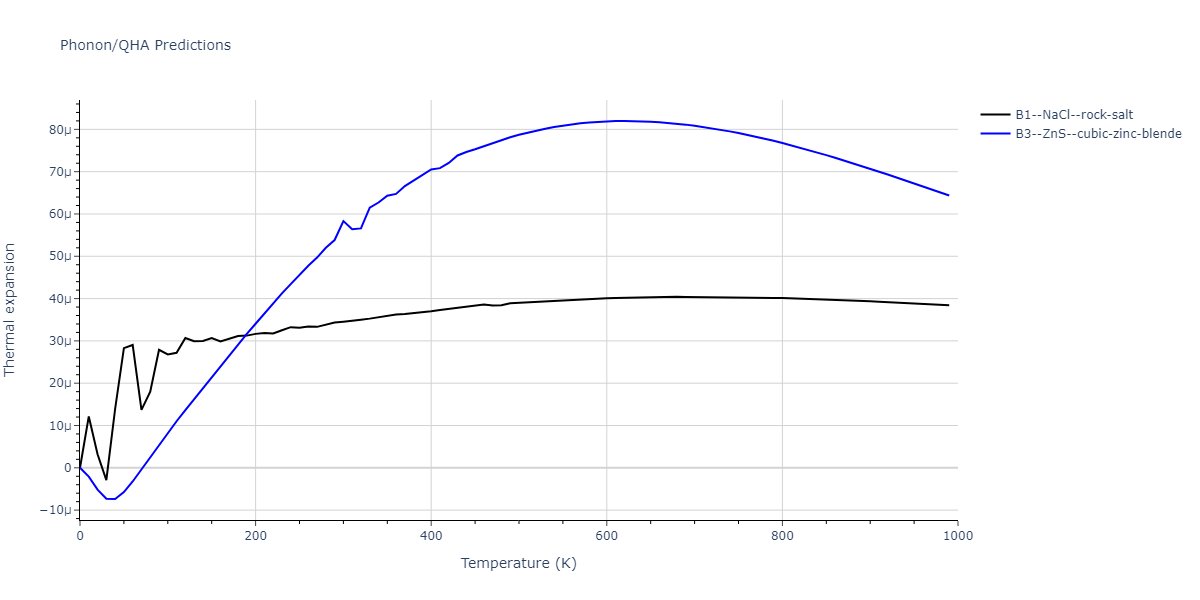
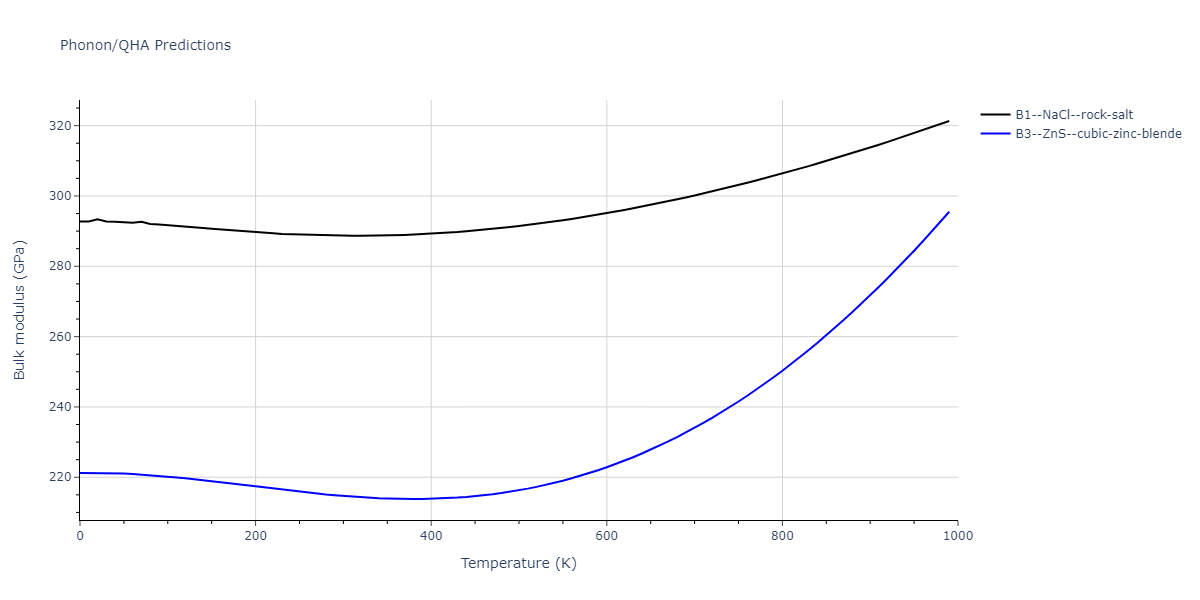
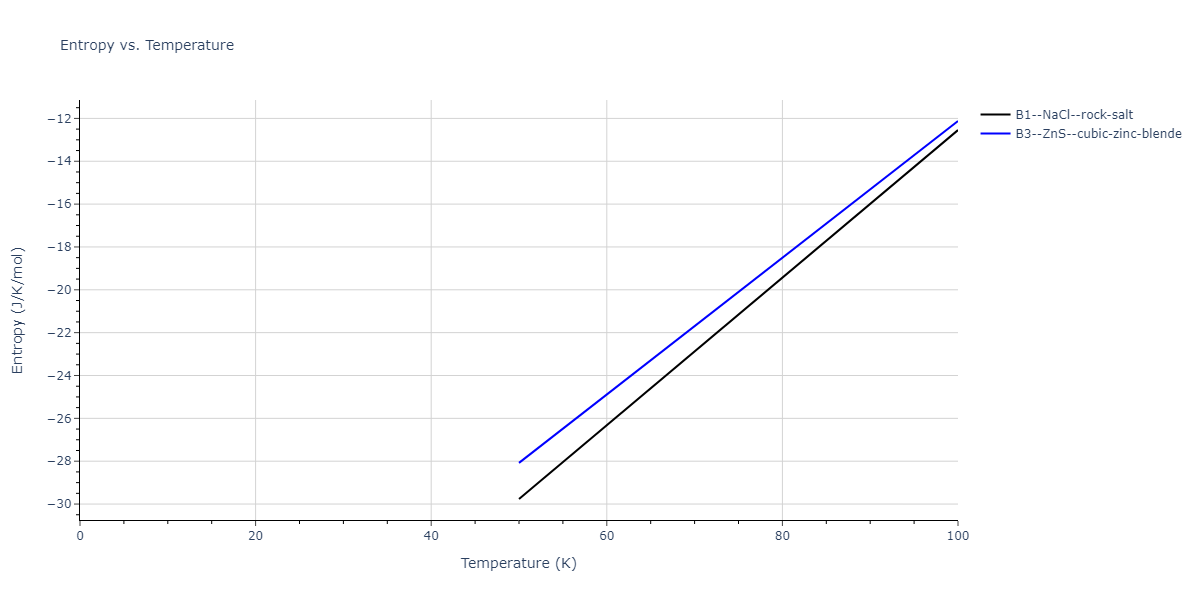
| B1--NaCl--rock-salt | static | -2.6489 | -2.6489 | 4.4239 | 4.4239 | 4.4239 | 90.0 | 90.0 | 90.0 |
| B4--ZnS--wurtzite | box | -2.4934 | -2.4934 | 3.3112 | 3.3112 | 4.9879 | 90.0 | 90.0 | 120.0 |
| B3--ZnS--cubic-zinc-blende | static | -2.4842 | -2.4842 | 4.5699 | 4.5699 | 4.5699 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-1214891 | dynamic | -2.1872 | -2.1872 | 16.0062 | 16.0062 | 16.0062 | 90.0 | 90.0 | 90.0 |
| mp-1214891 | static | -2.1872 | -2.1872 | 17.8384 | 17.8384 | 17.8384 | 90.0 | 90.0 | 90.0 |
| mp-1214891 | box | -2.1664 | -2.1664 | 11.0159 | 11.0159 | 11.0159 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| C1--CaF2--fluorite | static | -2.3612 | -2.3612 | 4.9198 | 4.9198 | 4.9198 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
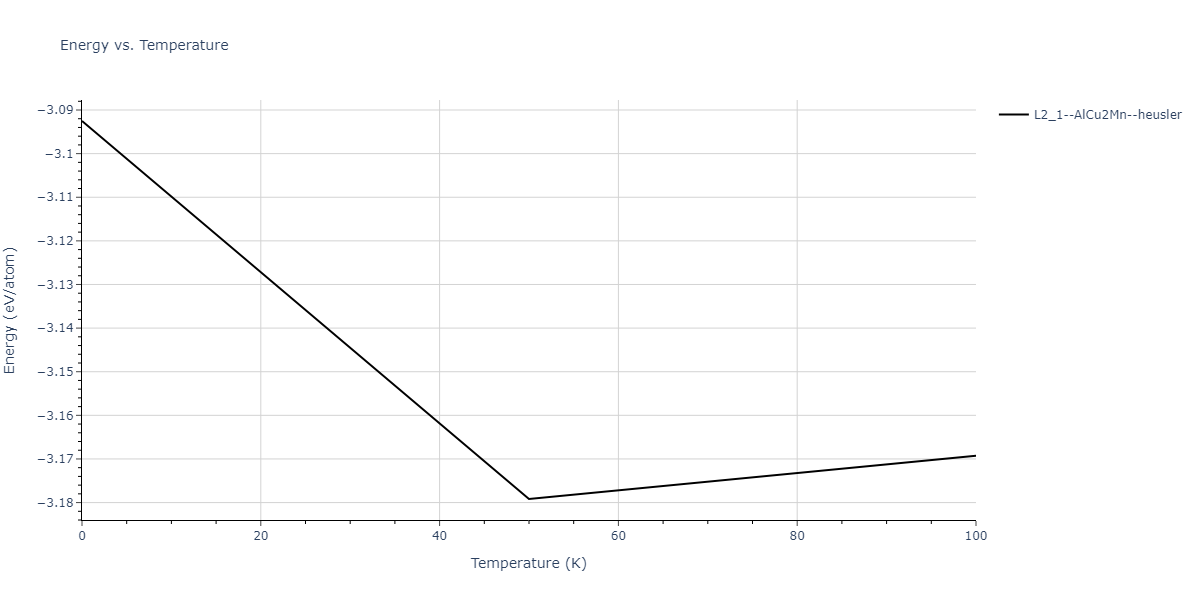
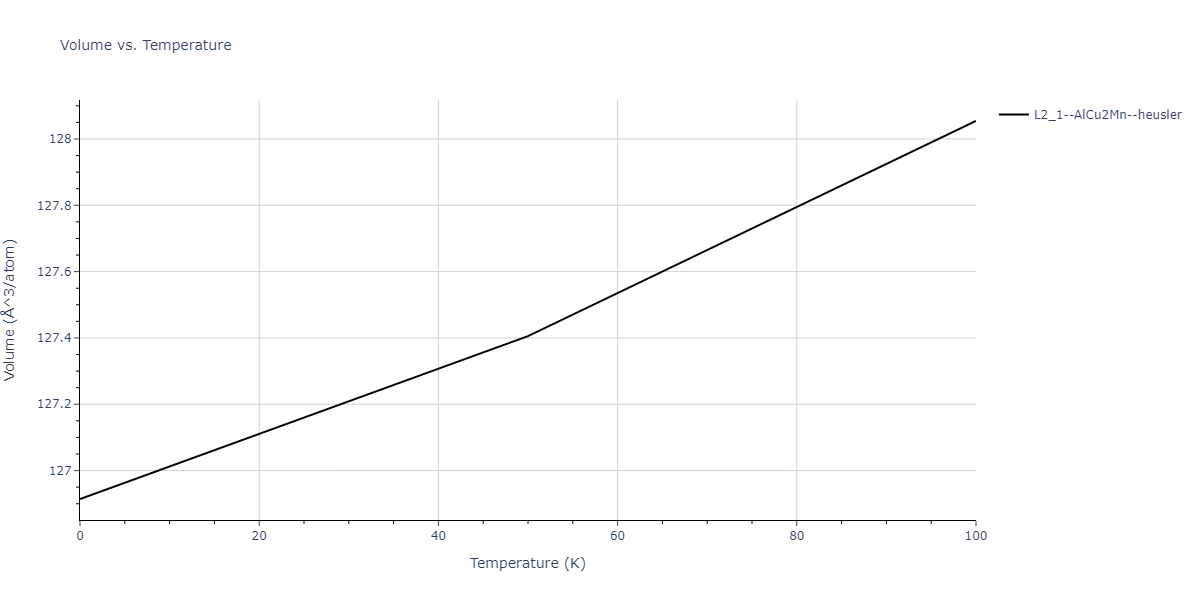
| L2_1--AlCu2Mn--heusler | dynamic | -3.0925 | -3.0925 | 5.0254 | 5.0254 | 5.0254 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
D0_3--BiF3 = oqmd-309483
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| A15--Cr3Si | dynamic | -2.333 | -2.333 | 4.064 | 4.064 | 4.064 | 90.0 | 90.0 | 90.0 |
| oqmd-298941 | static | -2.3274 | -2.3274 | 3.1761 | 3.1761 | 6.5274 | 90.0 | 90.0 | 90.0 |
| L1_2--AuCu3 | static | -2.3167 | -2.3167 | 3.1916 | 3.1916 | 3.1916 | 90.0 | 90.0 | 90.0 |
| D0_3--BiF3 | static | -2.3049 | -2.3049 | 5.037 | 5.037 | 5.037 | 90.0 | 90.0 | 90.0 |
| mp-1183246 | static | -2.2917 | -2.2917 | 7.1144 | 12.1251 | 5.1401 | 90.0 | 90.0 | 90.0 |
| oqmd-23083 | static | -2.2809 | -2.2809 | 7.2653 | 12.2709 | 5.1499 | 90.0 | 90.0 | 90.0 |
| mp-1106356 | box | -2.1189 | -2.1189 | 10.2382 | 10.2382 | 10.2382 | 90.0 | 90.0 | 90.0 |
| mp-1183246 | box | -2.1185 | -2.1185 | 7.3358 | 12.5335 | 7.08 | 90.0 | 90.0 | 90.0 |
| mp-570130 | box | -2.1123 | -2.1123 | 6.5371 | 7.8309 | 6.2861 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| L2_1--AlCu2Mn--heusler | static | -3.6358 | -3.6358 | 5.4843 | 5.4843 | 5.4843 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
B1--NaCl--rock-salt = oqmd-1103673
B2--CsCl = mp-1487, oqmd-10516, oqmd-94913, oqmd-94919, oqmd-304487
B3--ZnS--cubic-zinc-blende = oqmd-1218328
L1_0--AuCu = oqmd-336029
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| B2--CsCl | dynamic | -4.4254 | -4.4254 | 2.863 | 2.863 | 2.863 | 90.0 | 90.0 | 90.0 |
| oqmd-1217542 | box | -4.4253 | -4.4253 | 4.0489 | 2.8629 | 4.0491 | 90.0 | 90.0 | 90.0 |
| L1_0--AuCu | dynamic | -4.3966 | -4.3966 | 2.6521 | 2.6521 | 3.4684 | 90.0 | 90.0 | 90.0 |
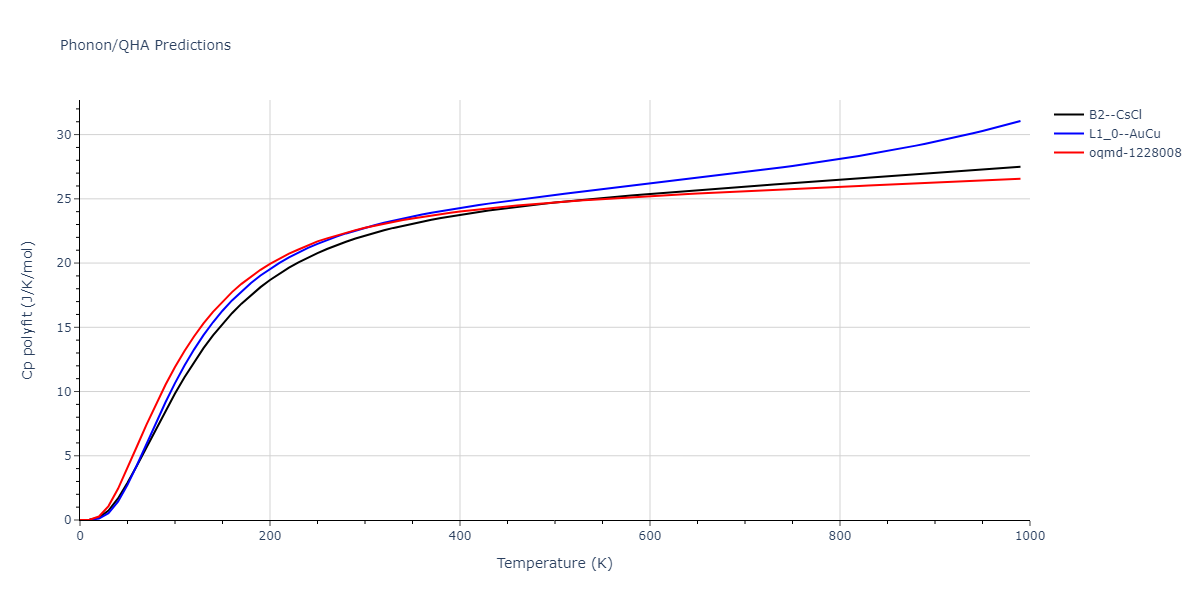
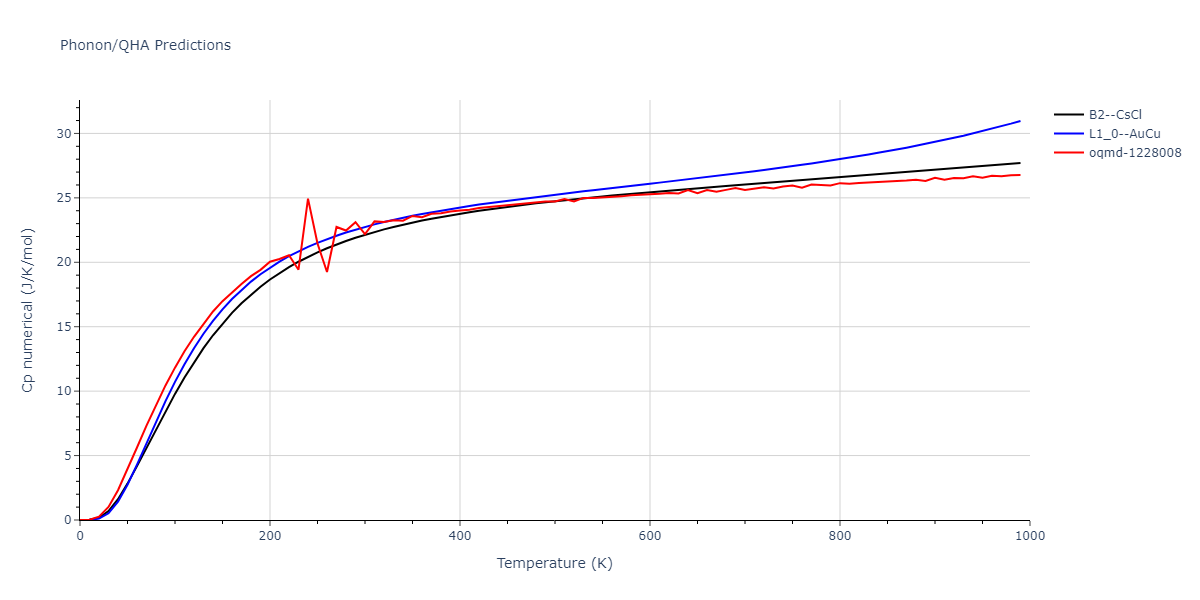
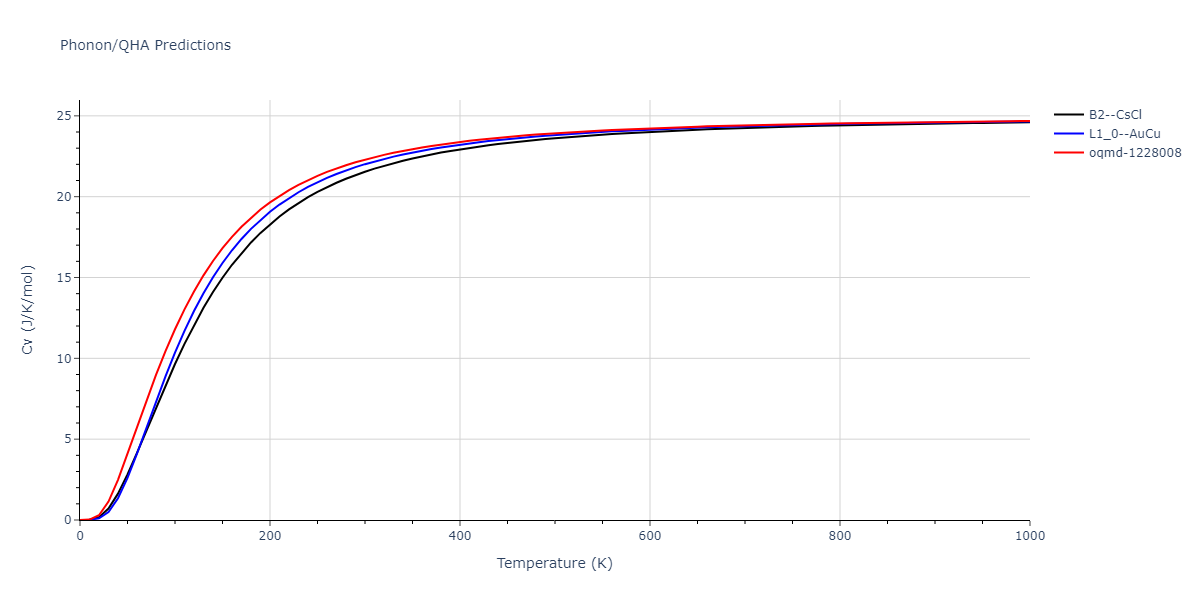
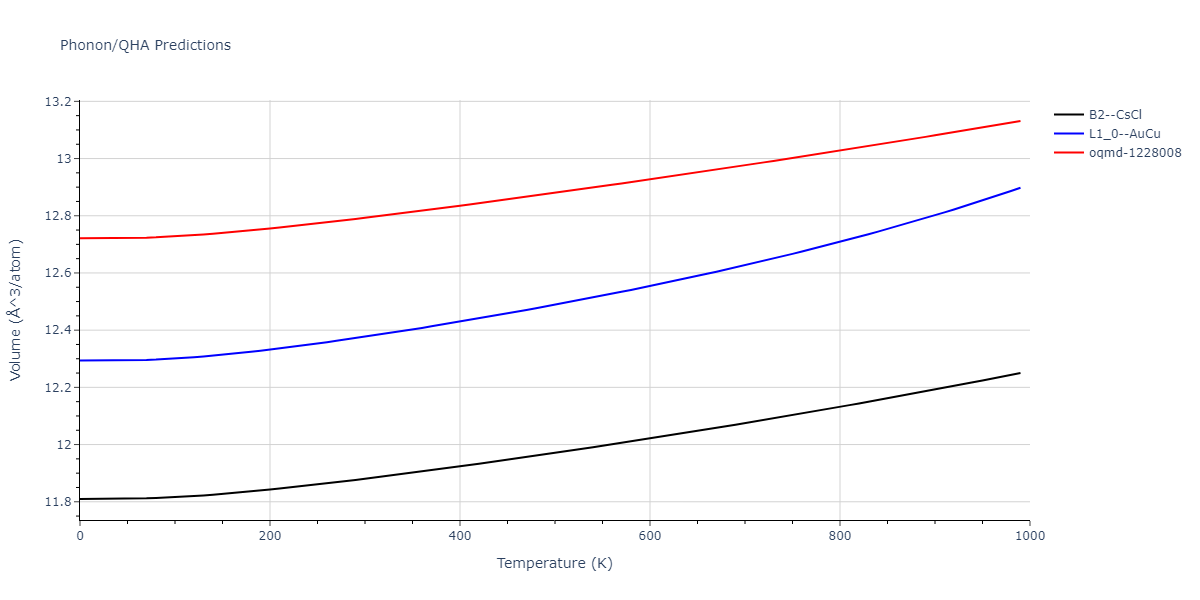
| oqmd-1228008 | dynamic | -4.3096 | -4.3096 | 2.689 | 2.689 | 4.0395 | 90.0 | 90.0 | 120.0 |
| oqmd-325571 | dynamic | -4.3016 | -4.3016 | 2.7052 | 2.7052 | 12.0008 | 90.0 | 90.0 | 120.0 |
| B1--NaCl--rock-salt | static | -3.9893 | -3.9893 | 4.9195 | 4.9195 | 4.9195 | 90.0 | 90.0 | 90.0 |
| oqmd-1224522 | box | -3.5662 | -3.5662 | 3.9815 | 3.9815 | 4.7788 | 90.0 | 90.0 | 120.0 |
| B3--ZnS--cubic-zinc-blende | static | -3.3682 | -3.3682 | 5.3186 | 5.3186 | 5.3186 | 90.0 | 90.0 | 90.0 |
| B4--ZnS--wurtzite | box | -3.3244 | -3.3244 | 3.762 | 3.762 | 6.2358 | 90.0 | 90.0 | 120.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-1025044 | dynamic | -4.5239 | -4.5239 | 4.0199 | 4.0199 | 4.9523 | 90.0 | 90.0 | 120.0 |
| mp-1025044 | box | -4.5177 | -4.5177 | 4.0287 | 4.0287 | 4.9281 | 90.0 | 90.0 | 120.0 |
| C1--CaF2--fluorite | static | -4.1508 | -4.1508 | 5.4939 | 5.4939 | 5.4939 | 90.0 | 90.0 | 90.0 |
| oqmd-1239580 | static | -1.8708 | -1.8708 | 10.4562 | 10.4562 | 10.4562 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
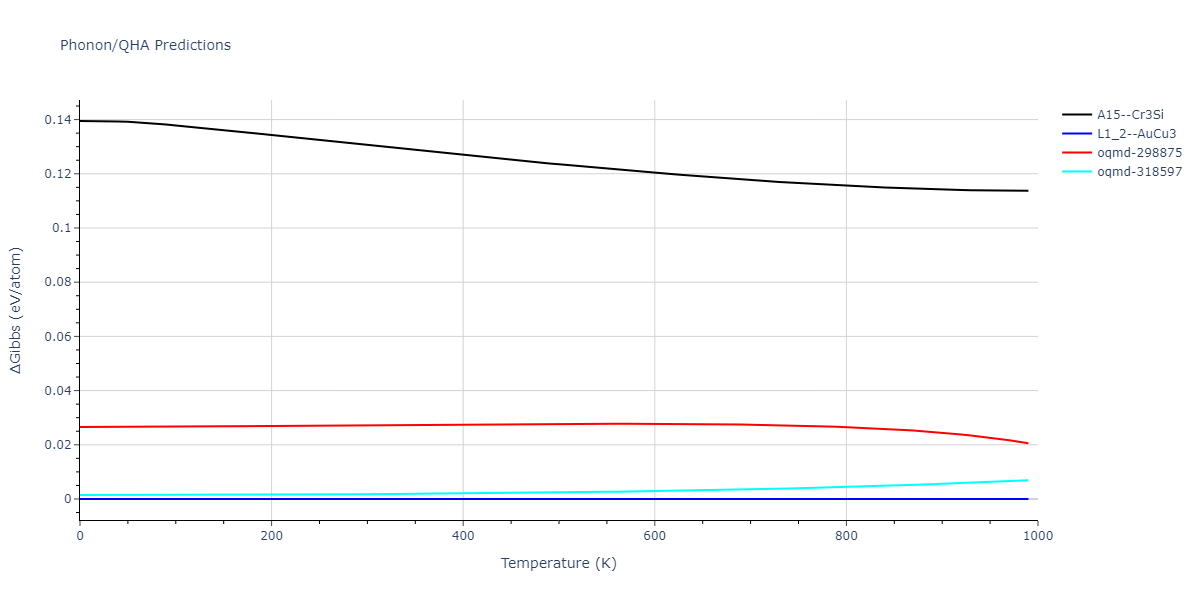
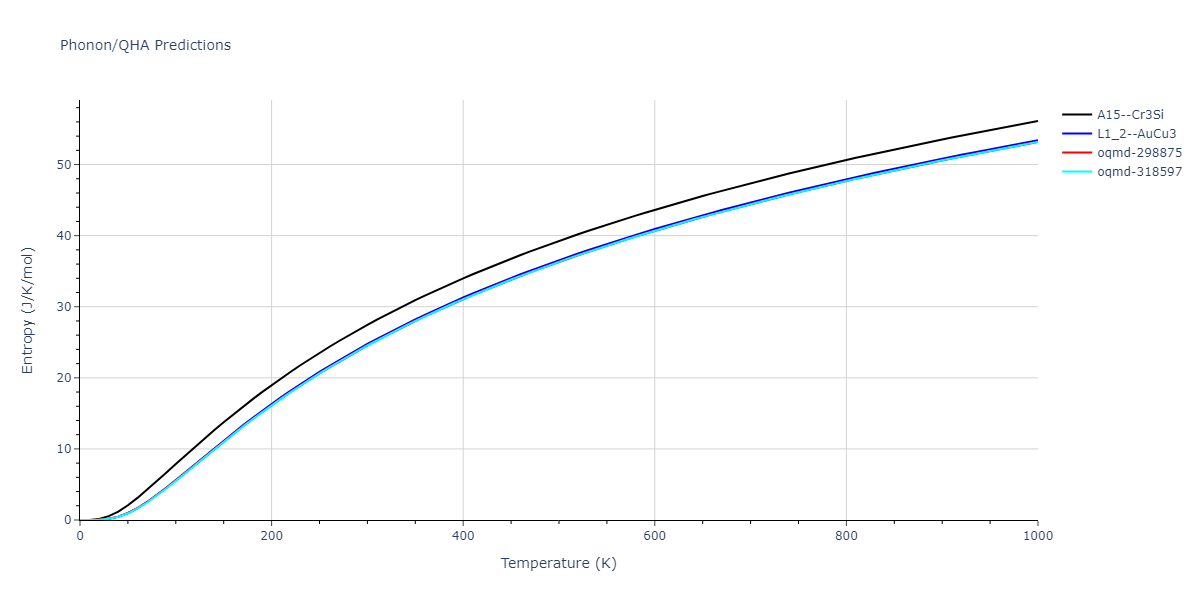
D0_3--BiF3 = mp-672232, oqmd-27902, oqmd-309416
L1_2--AuCu3 = mp-2593, oqmd-17890, oqmd-343083
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
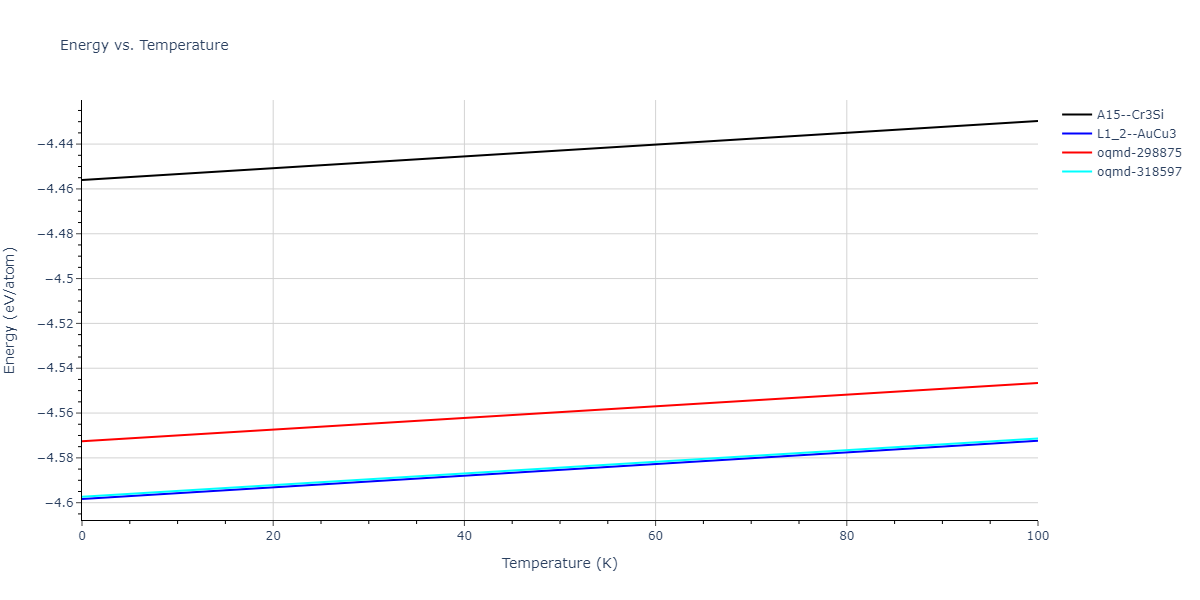
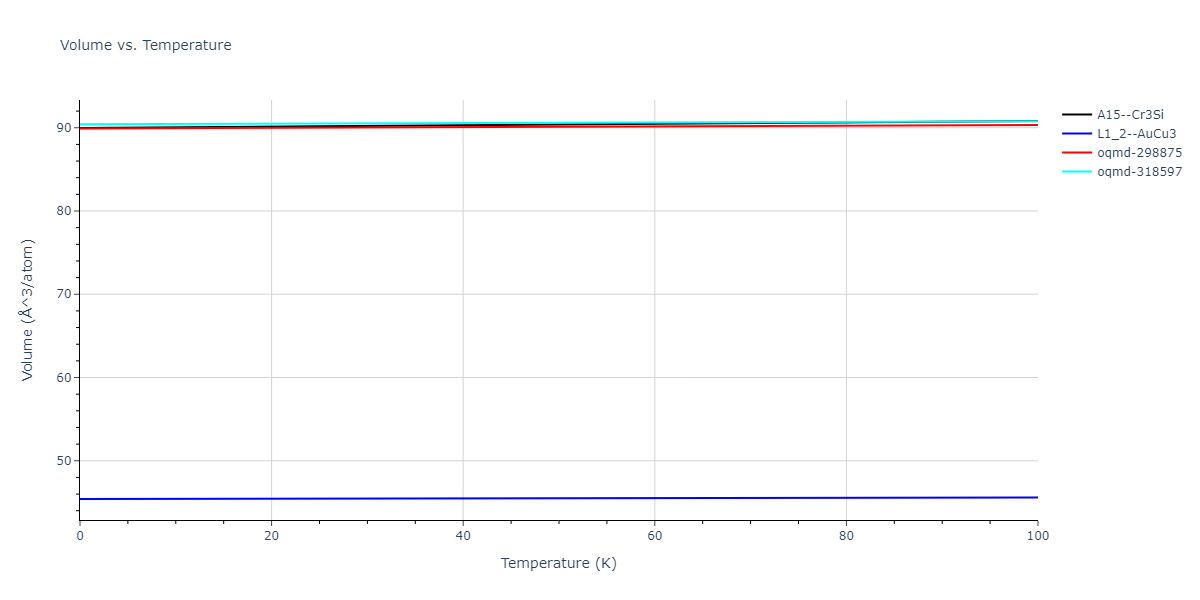
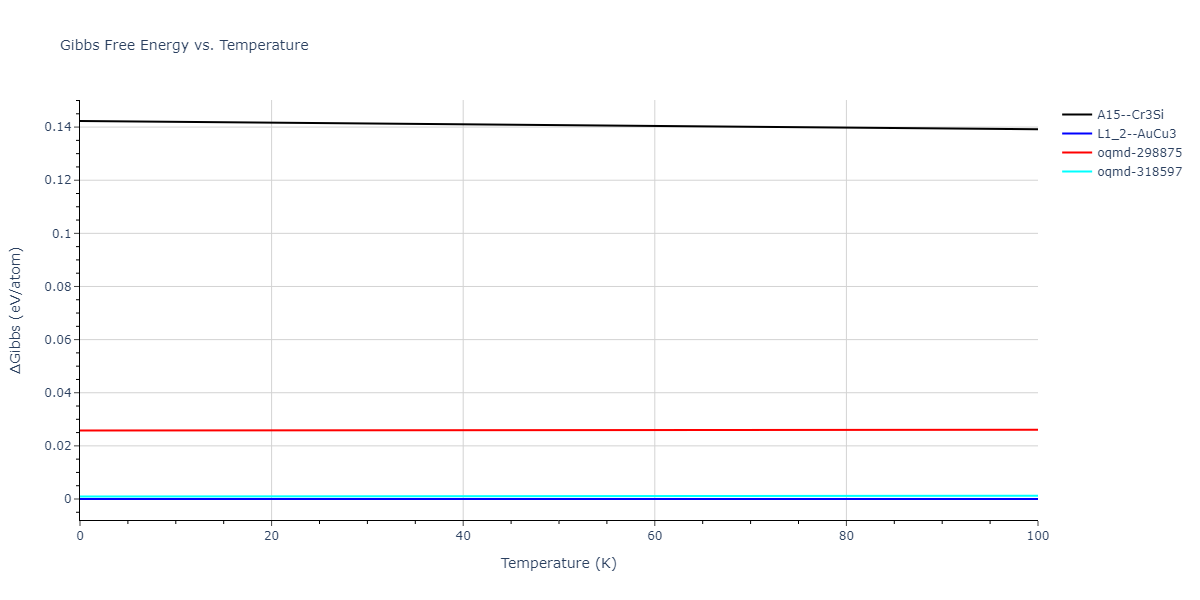
| L1_2--AuCu3 | dynamic | -4.5983 | -4.5983 | 3.5677 | 3.5677 | 3.5677 | 90.0 | 90.0 | 90.0 |
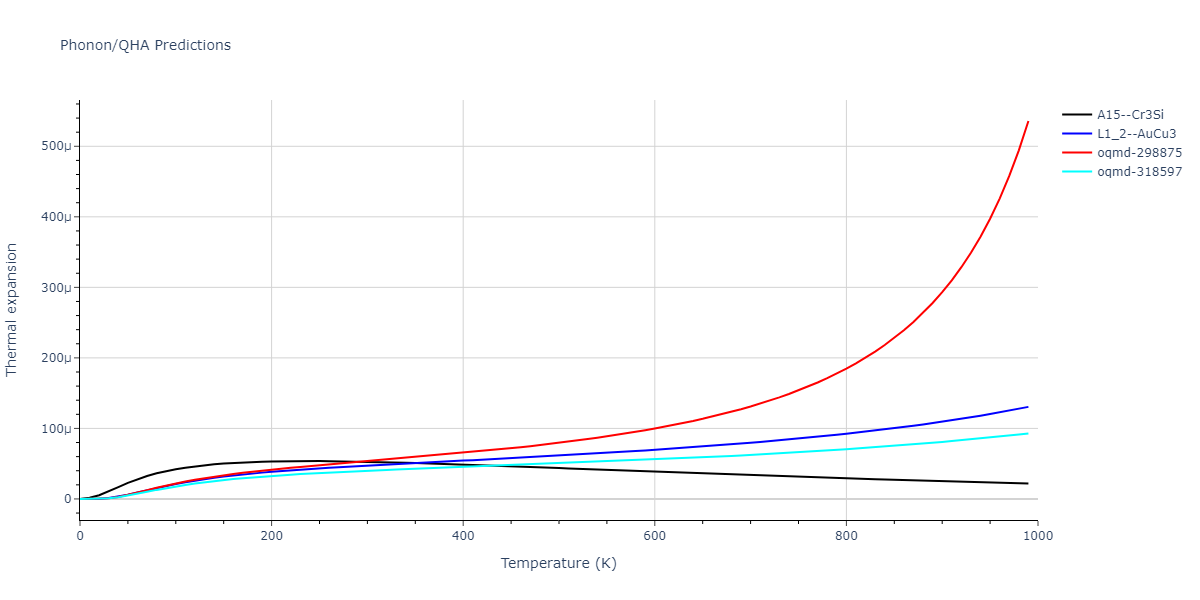
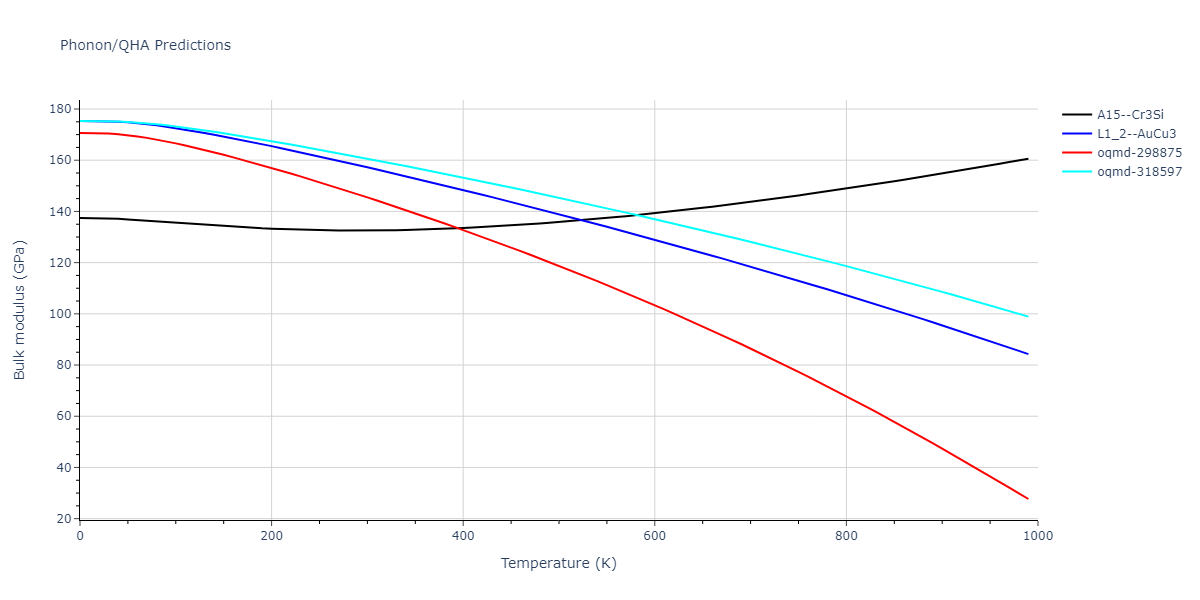
| oqmd-318597 | dynamic | -4.5974 | -4.5974 | 5.0399 | 5.0399 | 4.1109 | 90.0 | 90.0 | 120.0 |
| oqmd-318597 | box | -4.597 | -4.597 | 5.0417 | 5.0417 | 4.1099 | 90.0 | 90.0 | 120.0 |
| mp-1183232 | box | -4.5965 | -4.5965 | 5.0429 | 5.0429 | 4.1094 | 90.0 | 90.0 | 120.0 |
| oqmd-298875 | dynamic | -4.5726 | -4.5726 | 3.571 | 3.571 | 7.0509 | 90.0 | 90.0 | 90.0 |
| D0_3--BiF3 | static | -4.5341 | -4.5341 | 5.6671 | 5.6671 | 5.6671 | 90.0 | 90.0 | 90.0 |
| A15--Cr3Si | dynamic | -4.4561 | -4.4561 | 4.481 | 4.481 | 4.481 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
A1--Cu--fcc = mp-634659, oqmd-5497, oqmd-5499, oqmd-1214529
A15--beta-W = oqmd-1214974
A2--W--bcc = mp-632250, oqmd-5517, oqmd-1215152
A3'--alpha-La--double-hcp = oqmd-1215420
A3--Mg--hcp = mp-23907, mp-570752, oqmd-40867, oqmd-676625, oqmd-1215330
A4--C--dc = oqmd-1215509
A5--beta-Sn = oqmd-1215598
A6--In--bct = oqmd-1215687
A7--alpha-As = oqmd-1215776
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-1188177 | dynamic | -2.3695 | -2.3695 | 5.4783 | 7.1702 | 5.621 | 90.0 | 90.0 | 90.0 |
| mp-1188177 | static | -2.3695 | -2.3695 | 5.7015 | 6.6325 | 5.4662 | 90.0 | 90.0 | 90.0 |
| mp-1188177 | box | -2.3695 | -2.3695 | 5.7004 | 6.6161 | 5.474 | 90.0 | 90.0 | 90.0 |
| mp-24504 | static | -2.3695 | -2.3695 | 3.8401 | 3.8401 | 5.031 | 90.0 | 90.0 | 120.0 |
| mp-24504 | dynamic | -2.3695 | -2.3695 | 4.4704 | 4.4704 | 4.6448 | 90.0 | 90.0 | 120.0 |
| mp-632172 | dynamic | -2.3695 | -2.3695 | 4.4569 | 4.4569 | 3.9826 | 90.0 | 90.0 | 90.0 |
| mp-632291 | dynamic | -2.3695 | -2.3695 | 4.1788 | 4.1788 | 4.145 | 90.0 | 90.0 | 90.0 |
| mp-850274 | dynamic | -2.3695 | -2.3695 | 5.0317 | 5.0317 | 3.5546 | 90.0 | 90.0 | 90.0 |
| mp-850274 | static | -2.3695 | -2.3695 | 4.3181 | 4.3181 | 3.696 | 90.0 | 90.0 | 90.0 |
| mp-973783 | static | -2.3695 | -2.3695 | 5.2437 | 5.1239 | 4.1269 | 90.0 | 90.0 | 90.0 |
| mp-1066989 | dynamic | -2.3695 | -2.3695 | 3.8556 | 5.8524 | 6.3132 | 90.0 | 90.0 | 90.0 |
| mp-632172 | static | -2.3695 | -2.3695 | 4.4568 | 4.4568 | 3.499 | 90.0 | 90.0 | 90.0 |
| oqmd-5539 | static | -2.3695 | -2.3695 | 3.7457 | 3.7457 | 3.499 | 90.0 | 90.0 | 90.0 |
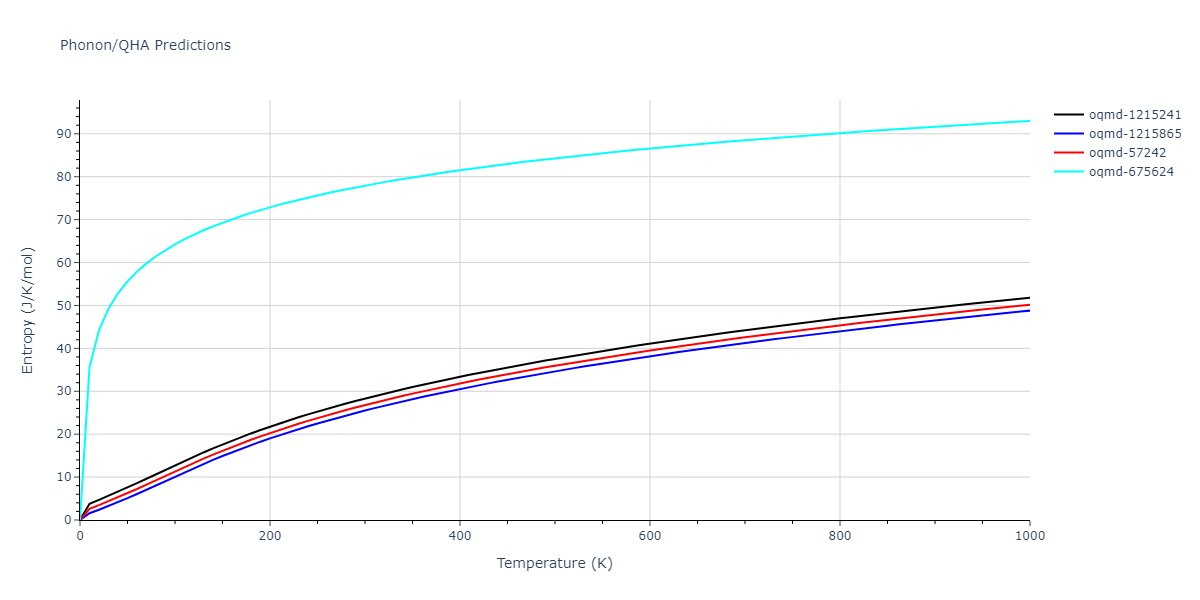
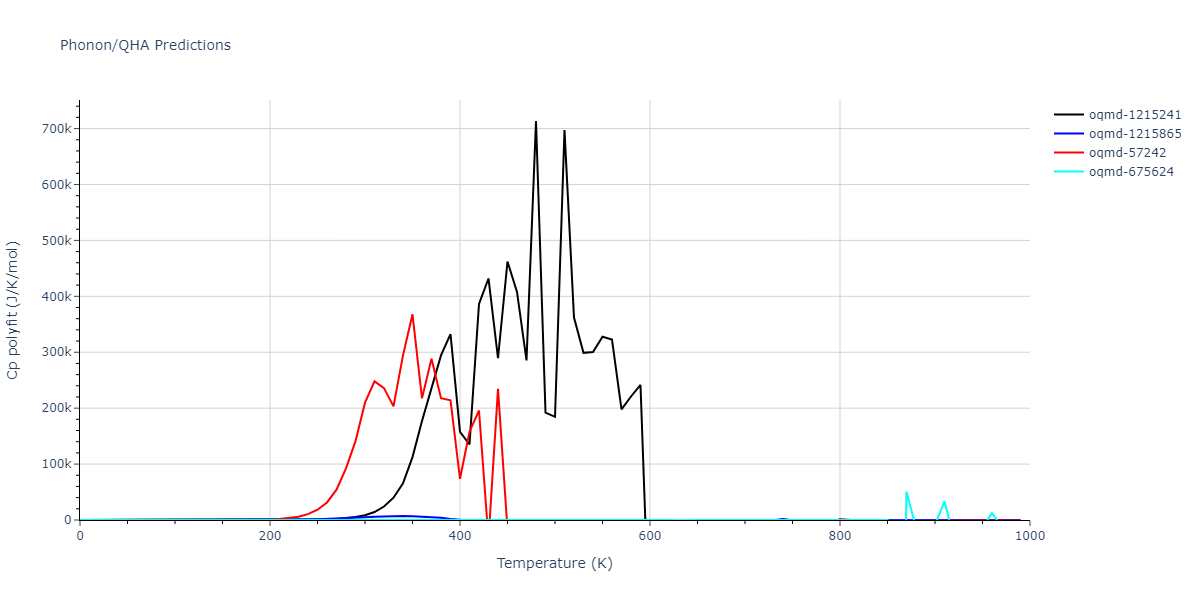
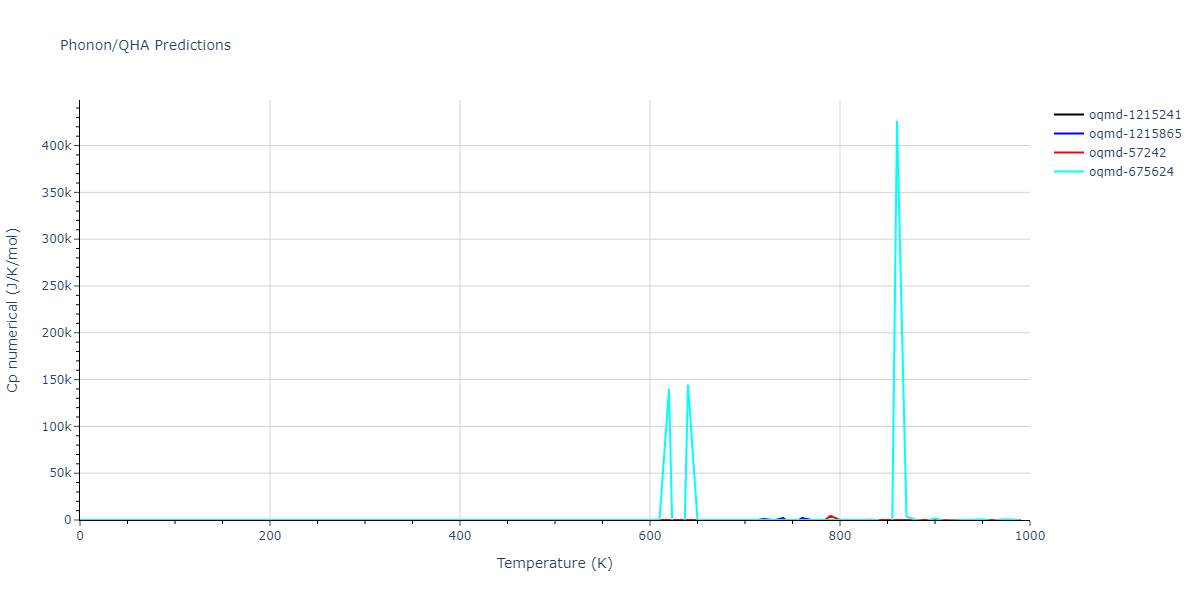
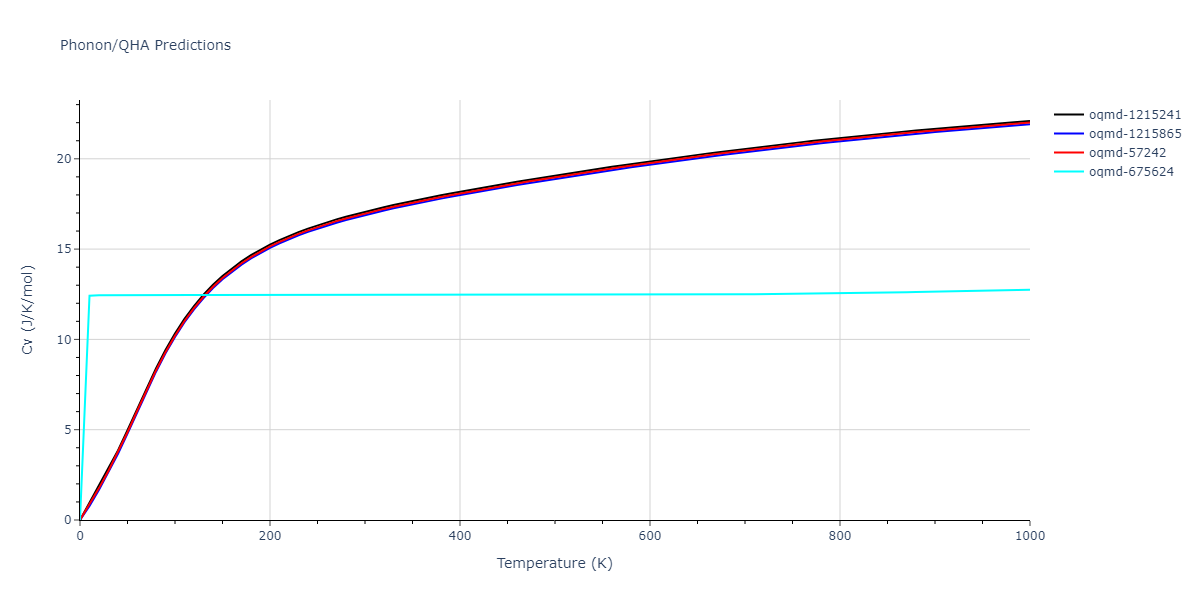
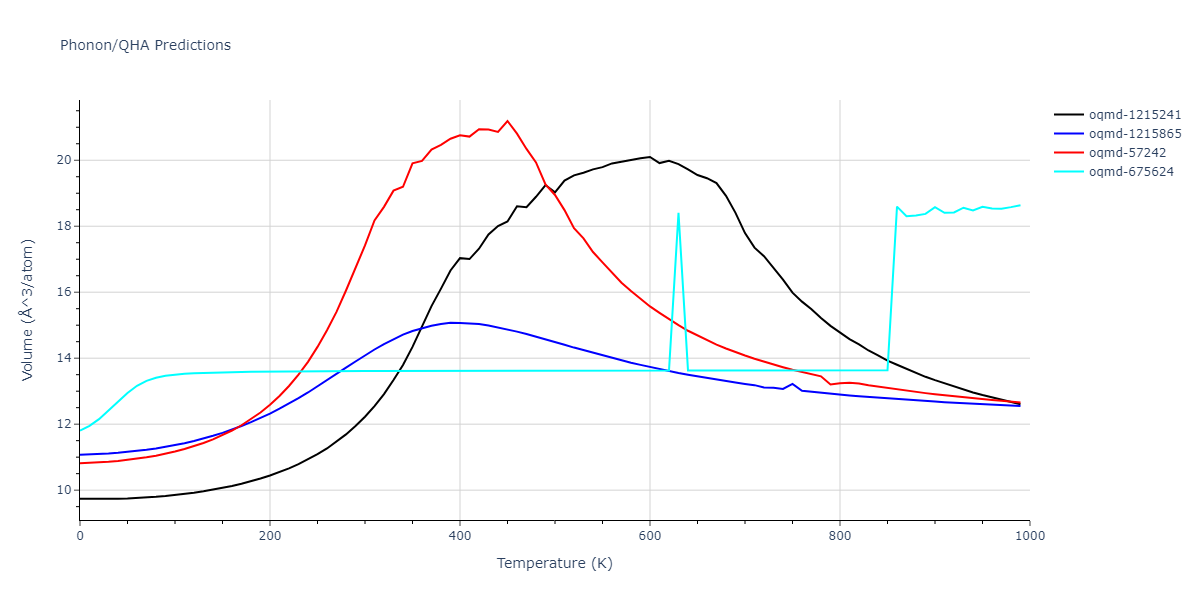
| oqmd-675624 | static | -2.3695 | -2.3695 | 3.7675 | 3.7675 | 3.499 | 90.0 | 90.0 | 90.0 |
| oqmd-11544 | static | -2.3695 | -2.3695 | 4.2822 | 4.2822 | 3.9306 | 90.0 | 90.0 | 120.0 |
| oqmd-1214707 | static | -2.3695 | -2.3695 | 4.831 | 4.831 | 4.1404 | 90.0 | 90.0 | 90.0 |
| mp-632291 | static | -2.3695 | -2.3695 | 3.4332 | 3.4332 | 4.1027 | 90.0 | 90.0 | 90.0 |
| oqmd-675624 | dynamic | -2.3695 | -2.3695 | 3.4685 | 3.4685 | 4.0081 | 90.0 | 90.0 | 90.0 |
| mp-1066989 | static | -2.3695 | -2.3695 | 3.8202 | 5.4548 | 6.3137 | 90.0 | 90.0 | 90.0 |
| mp-632291 | box | -2.3695 | -2.3695 | 3.425 | 3.425 | 4.1026 | 90.0 | 90.0 | 90.0 |
| mp-754417 | static | -2.3071 | -2.3071 | 2.8506 | 2.8506 | 1.0662 | 90.0 | 90.0 | 120.0 |
| mp-1096977 | dynamic | -2.3071 | -2.3071 | 3.2597 | 3.2597 | 1.0662 | 90.0 | 90.0 | 90.0 |
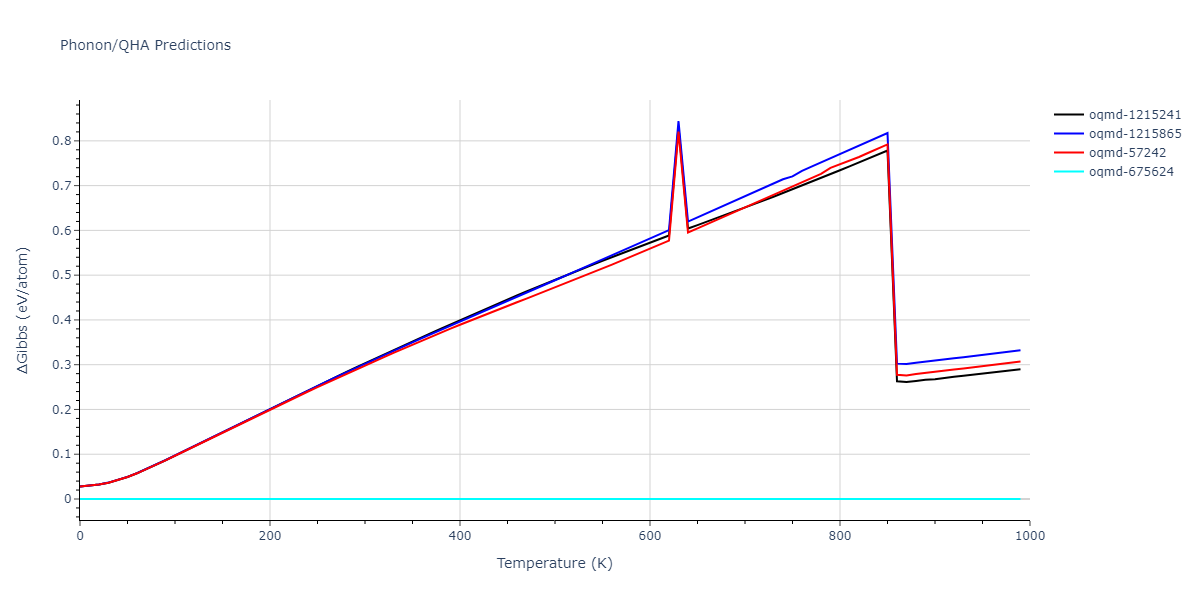
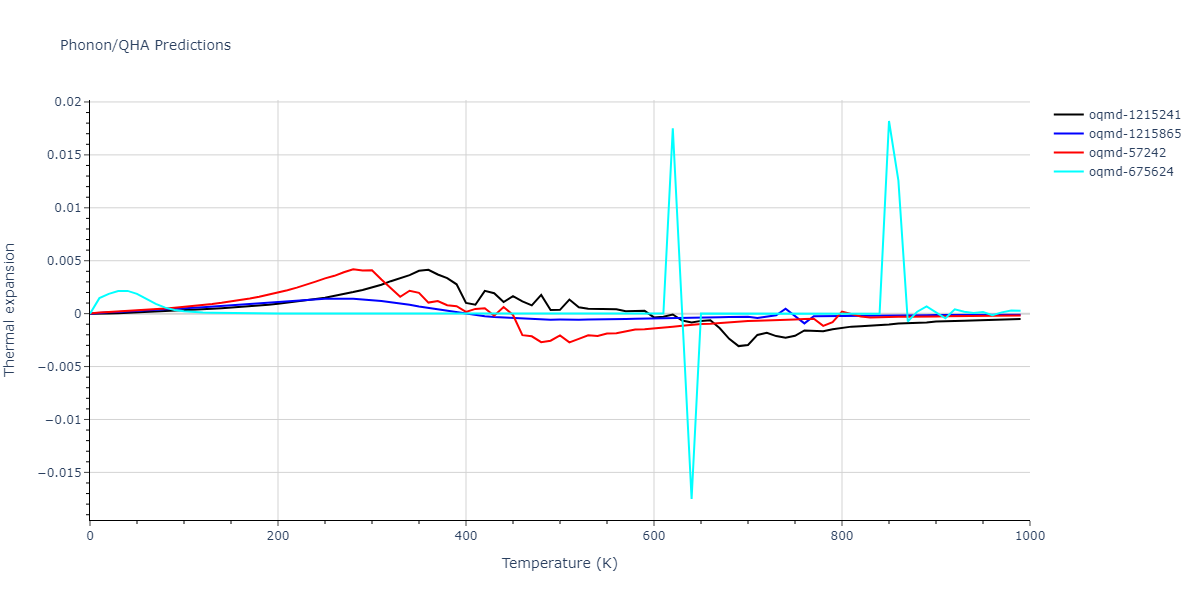
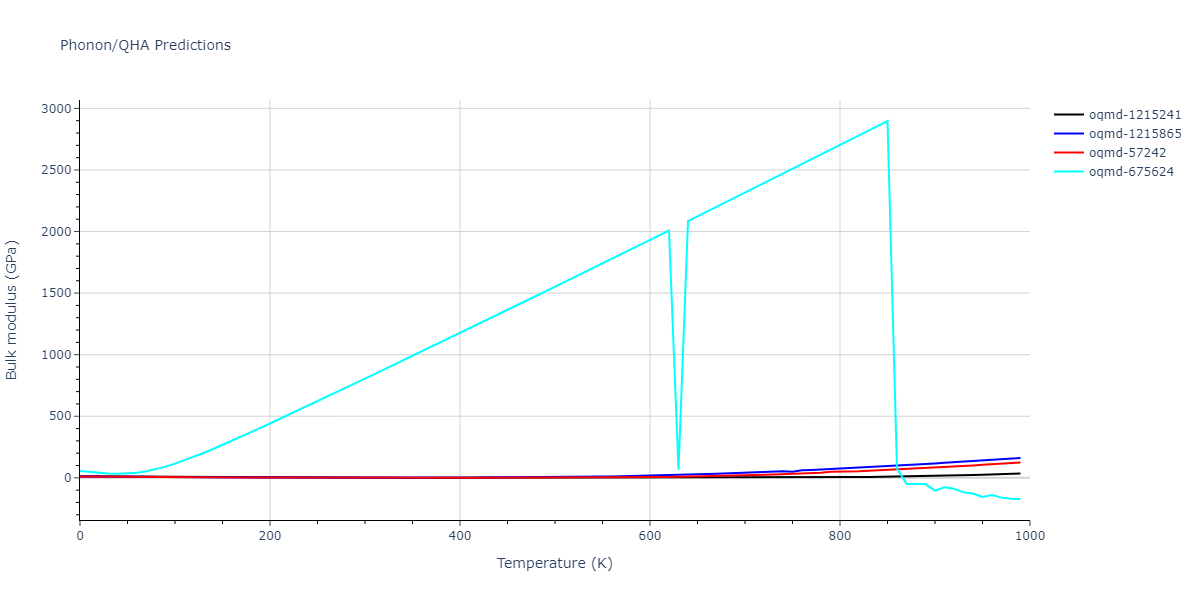
| oqmd-1215241 | dynamic | -2.3071 | -2.3071 | 3.2362 | 5.364 | 1.0662 | 90.0 | 90.0 | 90.0 |
| oqmd-1215865 | dynamic | -2.3071 | -2.3071 | 3.3764 | 3.3764 | 1.0662 | 90.0 | 90.0 | 120.0 |
| oqmd-57242 | dynamic | -2.3071 | -2.3071 | 1.0662 | 5.9621 | 3.2745 | 90.0 | 99.2 | 90.0 |
| mp-1096977 | static | -2.3071 | -2.3071 | 2.7594 | 2.7594 | 1.0662 | 90.0 | 90.0 | 90.0 |
| oqmd-57242 | static | -2.3071 | -2.3071 | 1.0662 | 4.7625 | 2.7594 | 90.0 | 100.3 | 90.0 |
| A5--beta-Sn | static | -2.3071 | -2.3071 | 5.493 | 5.493 | 1.0662 | 90.0 | 90.0 | 90.0 |
| oqmd-1215865 | static | -2.3071 | -2.3071 | 2.7594 | 2.7594 | 1.0662 | 90.0 | 90.0 | 120.0 |
| A3--Mg--hcp | static | -2.3071 | -2.3071 | 4.6886 | 4.6886 | 1.0662 | 90.0 | 90.0 | 120.0 |
| A5--beta-Sn | box | -2.3071 | -2.3071 | 5.4749 | 5.4749 | 1.0662 | 90.0 | 90.0 | 90.0 |
| oqmd-1215954 | box | -2.2123 | -2.2123 | 2.1319 | 2.1319 | 5.5007 | 90.0 | 90.0 | 120.0 |
| oqmd-1214796 | box | -2.1792 | -2.1792 | 6.97 | 6.97 | 6.97 | 90.0 | 90.0 | 90.0 |
| A4--C--dc | box | -2.1346 | -2.1346 | 3.1535 | 3.1535 | 3.1535 | 90.0 | 90.0 | 90.0 |
| A15--beta-W | static | -2.0824 | -2.0824 | 2.9952 | 2.9952 | 2.9952 | 90.0 | 90.0 | 90.0 |
| A3'--alpha-La--double-hcp | box | -2.0764 | -2.0764 | 1.9277 | 1.9277 | 4.3813 | 90.0 | 90.0 | 120.0 |
| A2--W--bcc | static | -2.0758 | -2.0758 | 1.8856 | 1.8856 | 1.8856 | 90.0 | 90.0 | 90.0 |
| A6--In--bct | box | -2.0758 | -2.0758 | 1.902 | 1.902 | 1.8543 | 90.0 | 90.0 | 90.0 |
| A3--Mg--hcp | box | -2.0727 | -2.0727 | 1.8376 | 1.8376 | 2.3812 | 90.0 | 90.0 | 120.0 |
| A6--In--bct | box | -2.0725 | -2.0725 | 1.6772 | 1.6772 | 2.4336 | 90.0 | 90.0 | 90.0 |
| A1--Cu--fcc | static | -2.0725 | -2.0725 | 2.3925 | 2.3925 | 2.3925 | 90.0 | 90.0 | 90.0 |
| A3'--alpha-La--double-hcp | box | -2.0725 | -2.0725 | 1.6918 | 1.6918 | 5.5252 | 90.0 | 90.0 | 120.0 |
| A3--Mg--hcp | box | -2.0725 | -2.0725 | 1.6918 | 1.6918 | 2.7626 | 90.0 | 90.0 | 120.0 |
| Ah--alpha-Po--sc | static | -2.0702 | -2.0702 | 1.5215 | 1.5215 | 1.5215 | 90.0 | 90.0 | 90.0 |
| A5--beta-Sn | box | -2.0591 | -2.0591 | 2.9215 | 2.9215 | 1.6461 | 90.0 | 90.0 | 90.0 |
| A3--Mg--hcp | dynamic | 0.0 | 0.0 | 5.1702 | 5.1702 | 3.8495 | 90.0 | 90.0 | 120.0 |
| A1--Cu--fcc | dynamic | 0.0 | 0.0 | 5.4286 | 5.4286 | 5.4286 | 90.0 | 90.0 | 90.0 |
| A3--Mg--hcp | dynamic | 0.0 | 0.0 | 3.9004 | 3.9004 | 6.3557 | 90.0 | 90.0 | 120.0 |
| A2--W--bcc | dynamic | 0.0 | 0.0 | 5.21 | 5.21 | 5.21 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| C1--CaF2--fluorite | dynamic | -2.9952 | -2.9952 | 4.0024 | 4.0024 | 4.0024 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
D0_3--BiF3 = oqmd-312022
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| D0_3--BiF3 | dynamic | -2.7547 | -2.7547 | 4.067 | 4.067 | 4.067 | 90.0 | 90.0 | 90.0 |
| A15--Cr3Si | dynamic | -2.717 | -2.717 | 3.2485 | 3.2485 | 3.2485 | 90.0 | 90.0 | 90.0 |
| L1_2--AuCu3 | static | -2.7127 | -2.7127 | 2.5862 | 2.5862 | 2.5862 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
B1--NaCl--rock-salt = mp-24719, oqmd-10077
B2--CsCl = oqmd-306427
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| B1--NaCl--rock-salt | dynamic | -3.4555 | -3.4555 | 3.7407 | 3.7407 | 3.7407 | 90.0 | 90.0 | 90.0 |
| B4--ZnS--wurtzite | box | -3.3485 | -3.3485 | 2.7579 | 2.7579 | 4.3606 | 90.0 | 90.0 | 120.0 |
| B3--ZnS--cubic-zinc-blende | dynamic | -3.3432 | -3.3432 | 3.8601 | 3.8601 | 3.8601 | 90.0 | 90.0 | 90.0 |
| B2--CsCl | static | -3.2968 | -3.2968 | 2.387 | 2.387 | 2.387 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| oqmd-22603 | box | -3.7569 | -3.7569 | 2.5627 | 2.5627 | 4.3137 | 90.0 | 90.0 | 120.0 |
| mp-753890 | box | -3.7564 | -3.7564 | 2.5623 | 2.5623 | 4.3144 | 90.0 | 90.0 | 120.0 |
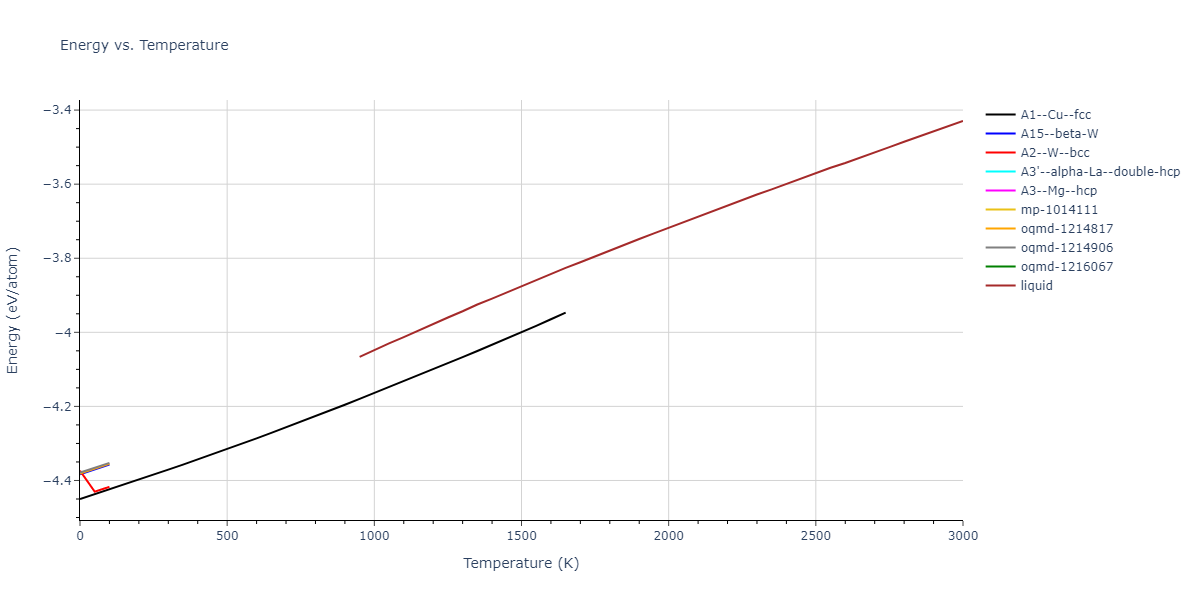
| mp-1220079 | dynamic | -3.7526 | -3.7526 | 2.588 | 2.588 | 12.632 | 90.0 | 90.0 | 120.0 |
| mp-1220079 | box | -3.7509 | -3.7509 | 2.5812 | 2.5812 | 12.6659 | 90.0 | 90.0 | 120.0 |
| C1--CaF2--fluorite | static | -3.5362 | -3.5362 | 4.7512 | 4.7512 | 4.7512 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
D0_3--BiF3 = mp-973895, oqmd-312485
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
| mp-976948 | box | -3.5267 | -3.5267 | 4.9796 | 4.9796 | 3.5563 | 90.0 | 90.0 | 120.0 |
| oqmd-301943 | static | -3.4844 | -3.4844 | 3.4141 | 3.4141 | 6.6903 | 90.0 | 90.0 | 90.0 |
| L1_2--AuCu3 | static | -3.481 | -3.481 | 3.4025 | 3.4025 | 3.4025 | 90.0 | 90.0 | 90.0 |
| D0_3--BiF3 | static | -3.4428 | -3.4428 | 5.3656 | 5.3656 | 5.3656 | 90.0 | 90.0 | 90.0 |
| A15--Cr3Si | static | -3.4107 | -3.4107 | 4.2703 | 4.2703 | 4.2703 | 90.0 | 90.0 | 90.0 |
Download raw data (including filtered results)
Reference structure matches:
A1--Cu--fcc = mp-23, oqmd-676148, oqmd-1214550
A15--beta-W = oqmd-1214995, oqmd-1280360
A2--W--bcc = mp-1008728, oqmd-22516, oqmd-1215173
A3'--alpha-La--double-hcp = oqmd-1215441
A3--Mg--hcp = mp-10257, oqmd-677944, oqmd-1215351
A4--C--dc = oqmd-1215530
A5--beta-Sn = oqmd-1215619
A6--In--bct = oqmd-1215708
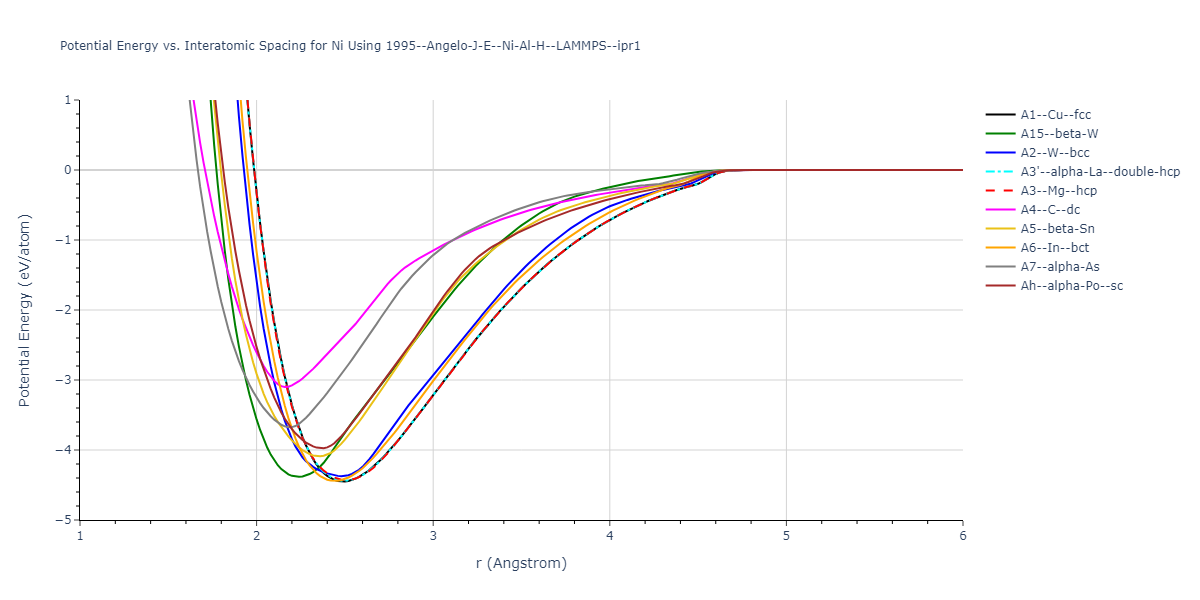
| prototype | method | Ecoh (eV/atom) | Epot (eV/atom) | a0 (Å) | b0 (Å) | c0 (Å) | α (degrees) | β (degrees) | γ (degrees) |
|---|---|---|---|---|---|---|---|---|---|
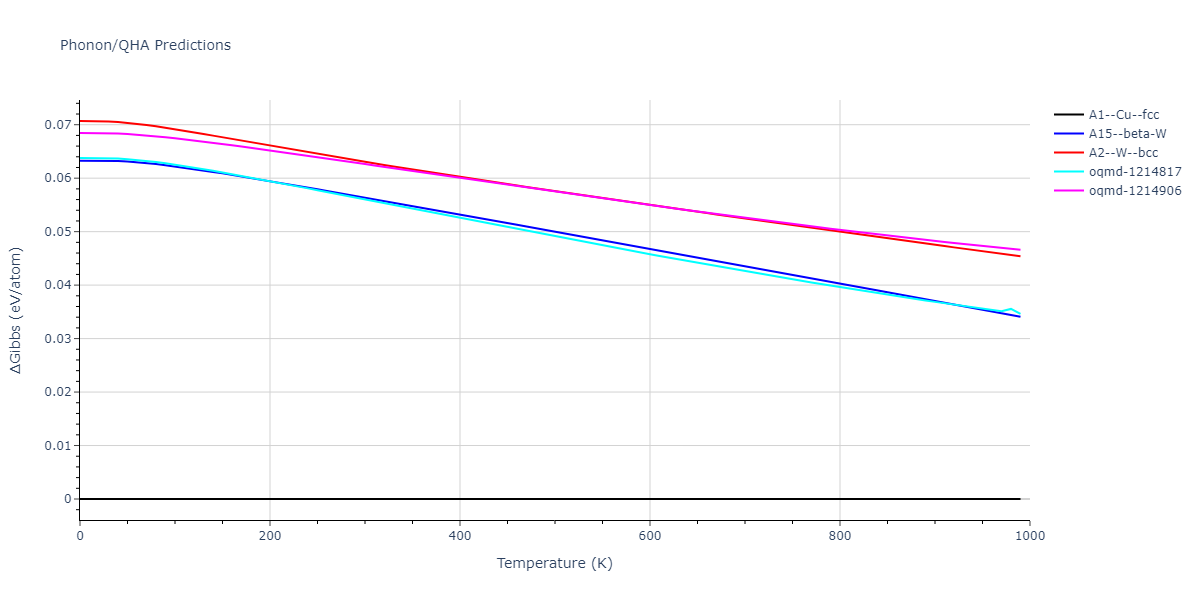
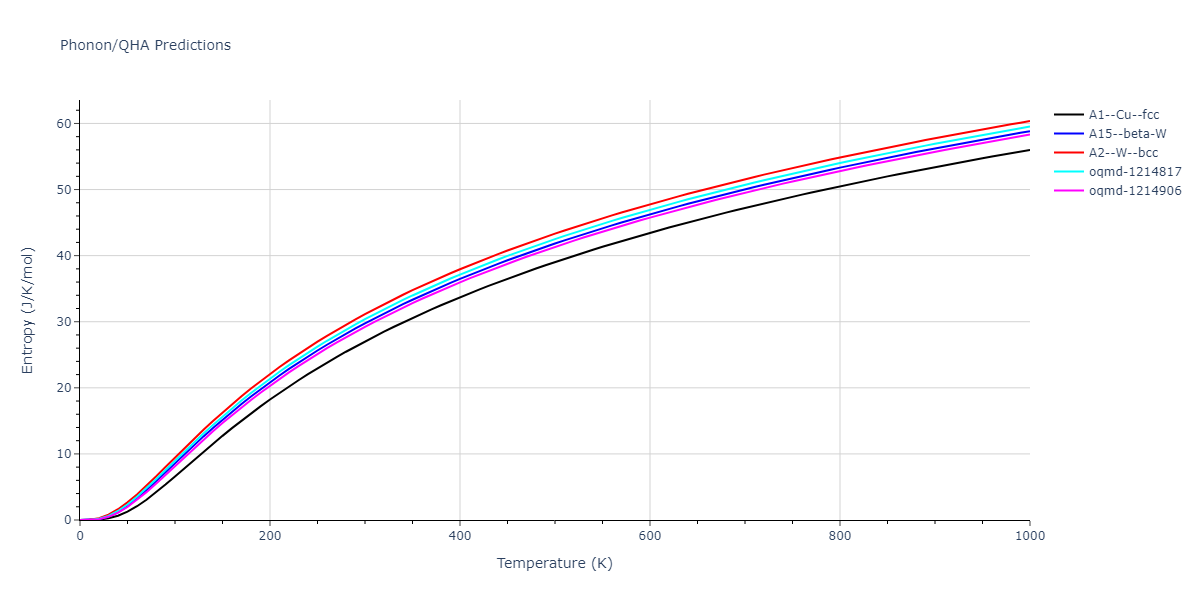
| A1--Cu--fcc | dynamic | -4.45 | -4.45 | 3.52 | 3.52 | 3.52 | 90.0 | 90.0 | 90.0 |
| A3'--alpha-La--double-hcp | dynamic | -4.4417 | -4.4417 | 2.484 | 2.484 | 8.2469 | 90.0 | 90.0 | 120.0 |
| oqmd-1216067 | dynamic | -4.4403 | -4.4403 | 2.4826 | 2.4826 | 18.6388 | 90.0 | 90.0 | 120.0 |
| A3--Mg--hcp | dynamic | -4.4374 | -4.4374 | 2.4796 | 2.4796 | 4.1786 | 90.0 | 90.0 | 120.0 |
| oqmd-1215262 | box | -4.437 | -4.437 | 2.4739 | 4.3046 | 4.1791 | 90.0 | 90.0 | 90.0 |
| A15--beta-W | dynamic | -4.383 | -4.383 | 4.4724 | 4.4724 | 4.4724 | 90.0 | 90.0 | 90.0 |
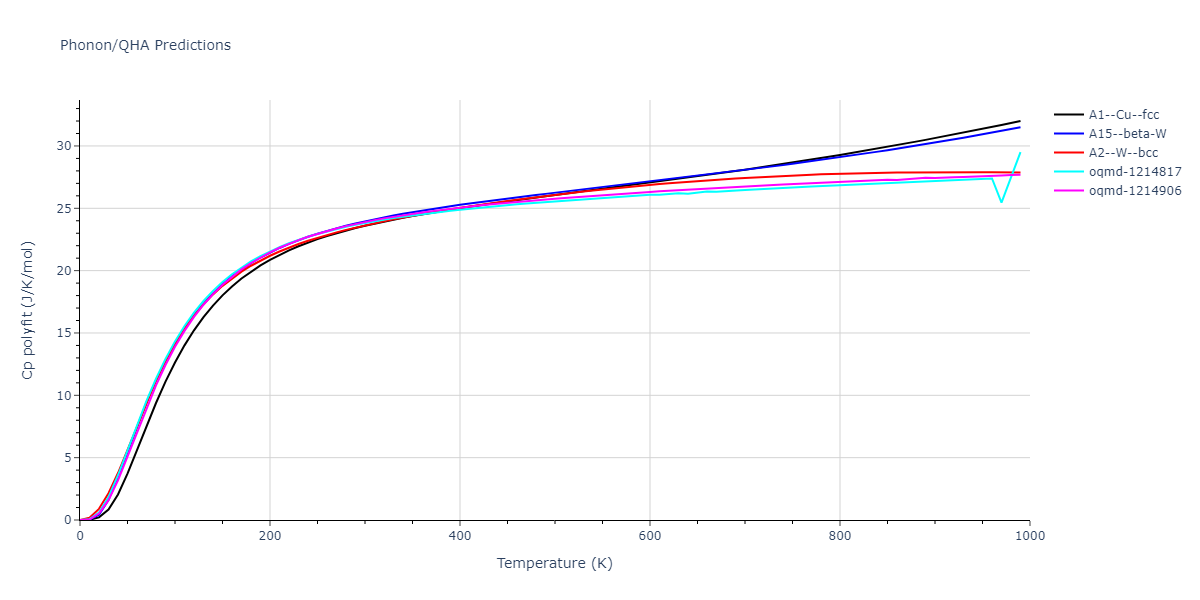
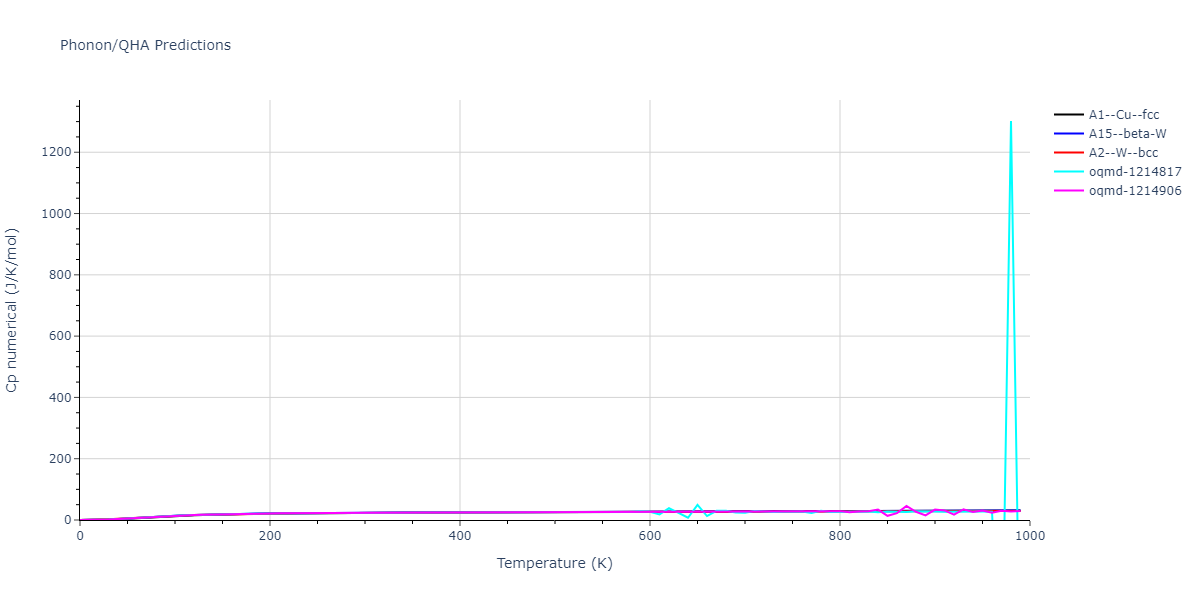
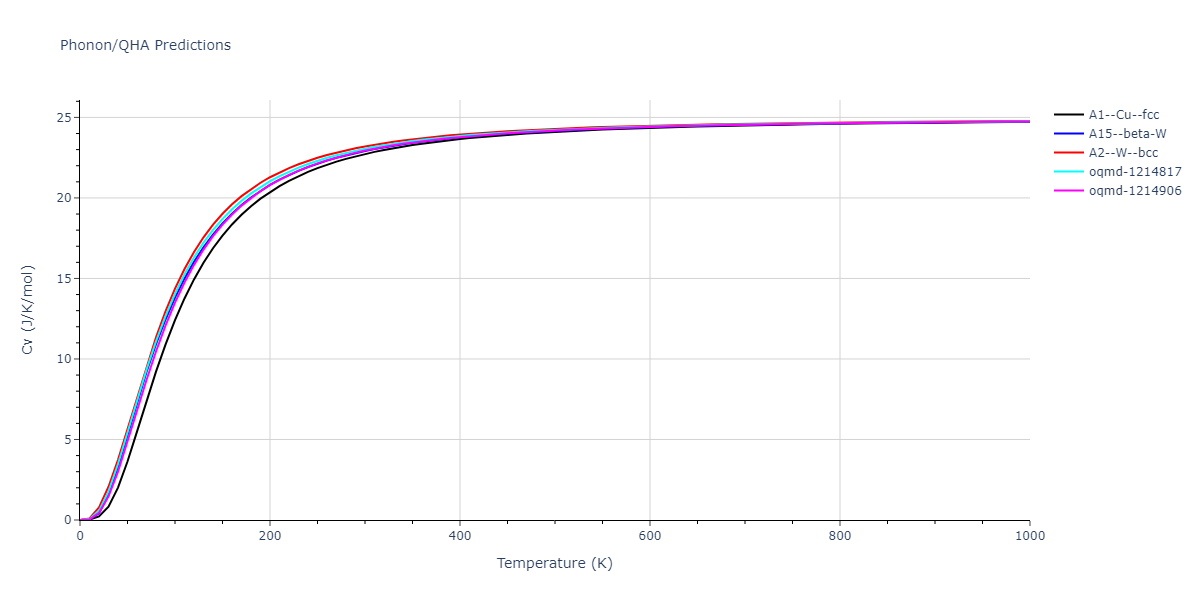
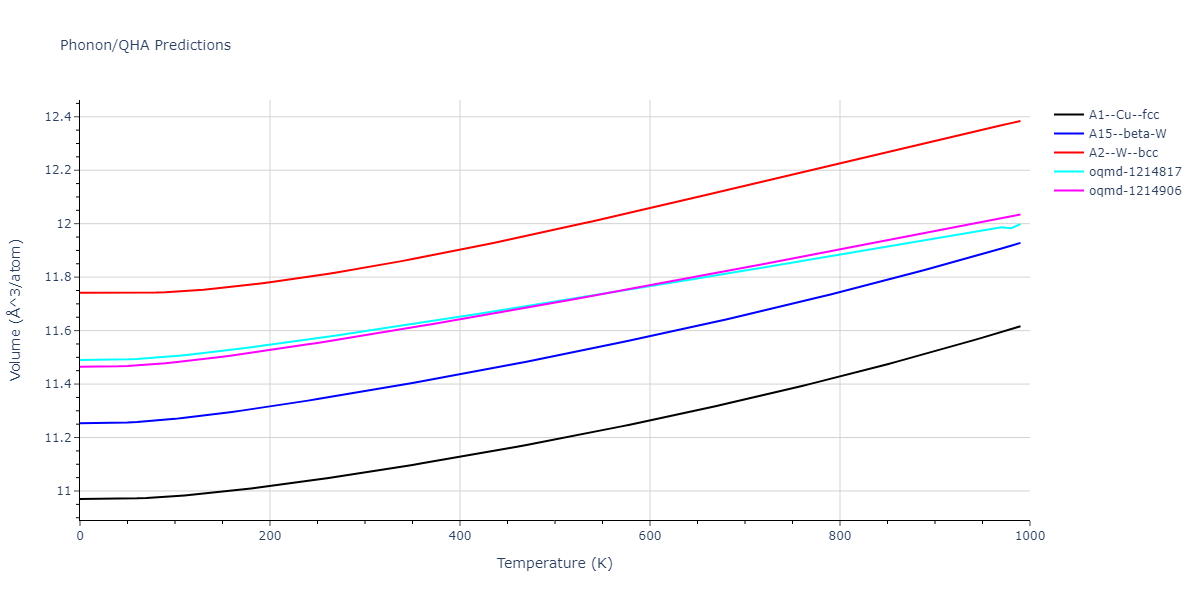
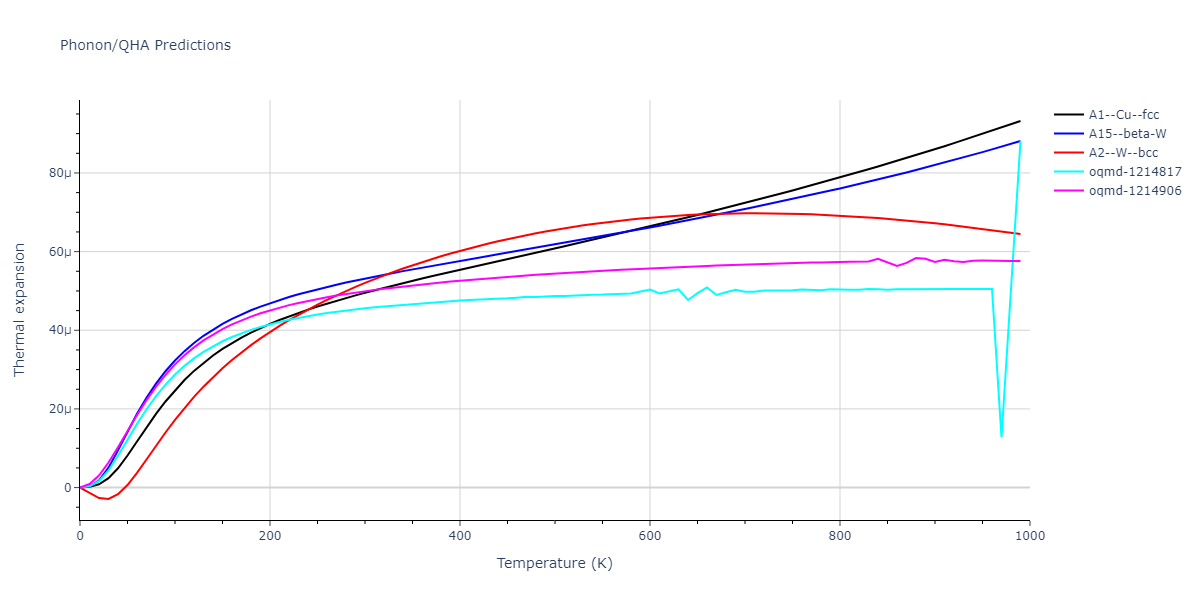
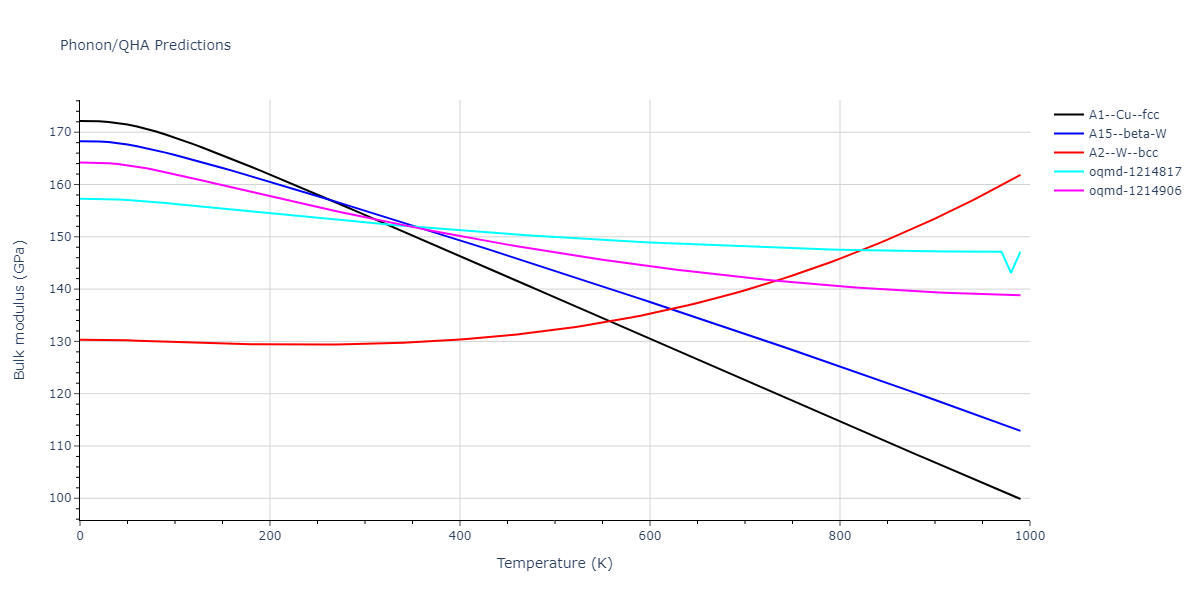
| oqmd-1214817 | dynamic | -4.3812 | -4.3812 | 8.7157 | 8.7157 | 8.7157 | 90.0 | 90.0 | 90.0 |
| oqmd-1214817 | box | -4.3804 | -4.3804 | 8.7117 | 8.7117 | 8.7117 | 90.0 | 90.0 | 90.0 |
| oqmd-1214906 | dynamic | -4.3785 | -4.3785 | 6.1059 | 6.1059 | 6.1059 | 90.0 | 90.0 | 90.0 |
| oqmd-1214906 | box | -4.3771 | -4.3771 | 6.1055 | 6.1055 | 6.1055 | 90.0 | 90.0 | 90.0 |
| A2--W--bcc | dynamic | -4.3736 | -4.3736 | 2.8659 | 2.8659 | 2.8659 | 90.0 | 90.0 | 90.0 |
| oqmd-1215084 | box | -4.2694 | -4.2694 | 2.4889 | 4.2744 | 9.1698 | 90.0 | 90.0 | 90.0 |
| oqmd-1214728 | box | -4.1638 | -4.1638 | 2.4401 | 2.4401 | 8.235 | 90.0 | 90.0 | 90.0 |
| A5--beta-Sn | box | -4.0941 | -4.0941 | 4.5924 | 4.5924 | 2.4504 | 90.0 | 90.0 | 90.0 |
| Ah--alpha-Po--sc | static | -3.975 | -3.975 | 2.3689 | 2.3689 | 2.3689 | 90.0 | 90.0 | 90.0 |
| mp-1014111 | static | -3.8147 | -3.8147 | 2.4422 | 2.4422 | 13.6624 | 90.0 | 90.0 | 120.0 |
| mp-1014111 | dynamic | -3.8147 | -3.8147 | 2.4422 | 2.4422 | 13.623 | 90.0 | 90.0 | 120.0 |
| A7--alpha-As | box | -3.637 | -3.637 | 3.0916 | 3.0916 | 10.2103 | 90.0 | 90.0 | 120.0 |
| oqmd-1215975 | box | -3.5229 | -3.5229 | 3.8808 | 3.8808 | 4.2976 | 90.0 | 90.0 | 120.0 |
| A4--C--dc | static | -3.1017 | -3.1017 | 4.9976 | 4.9976 | 4.9976 | 90.0 | 90.0 | 90.0 |
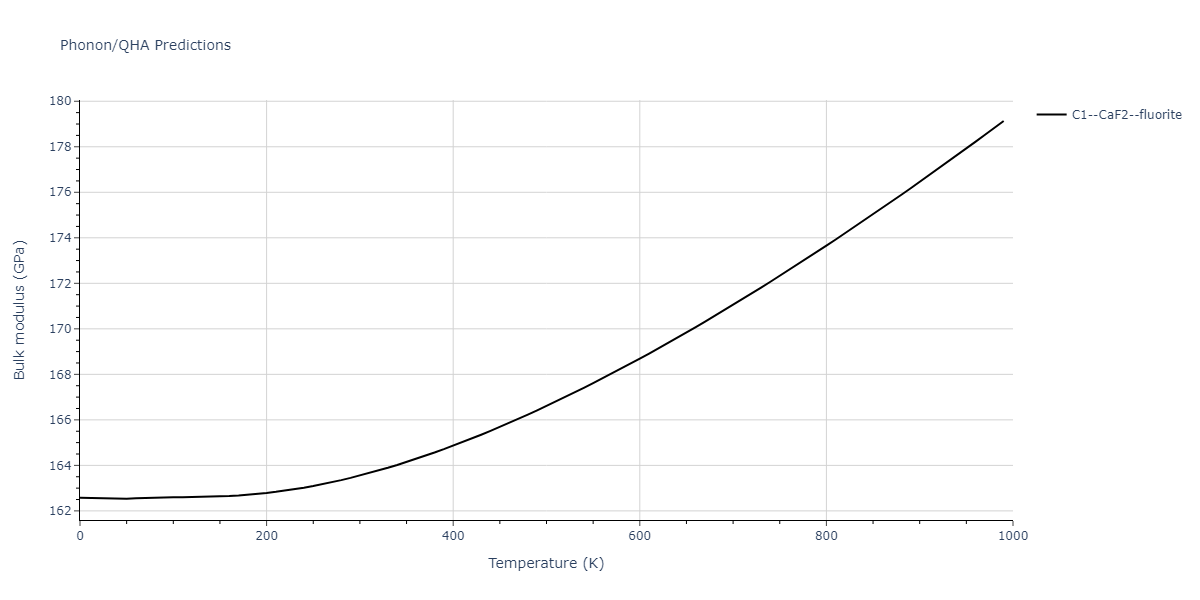
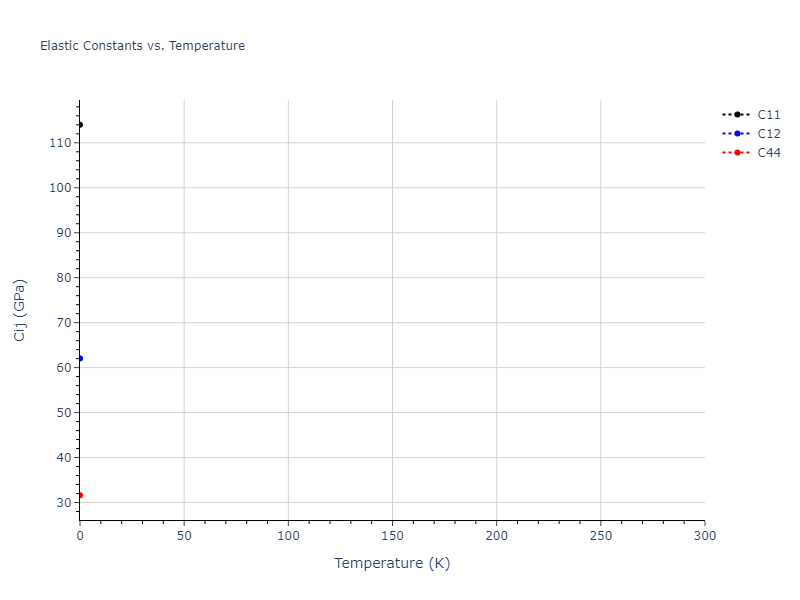
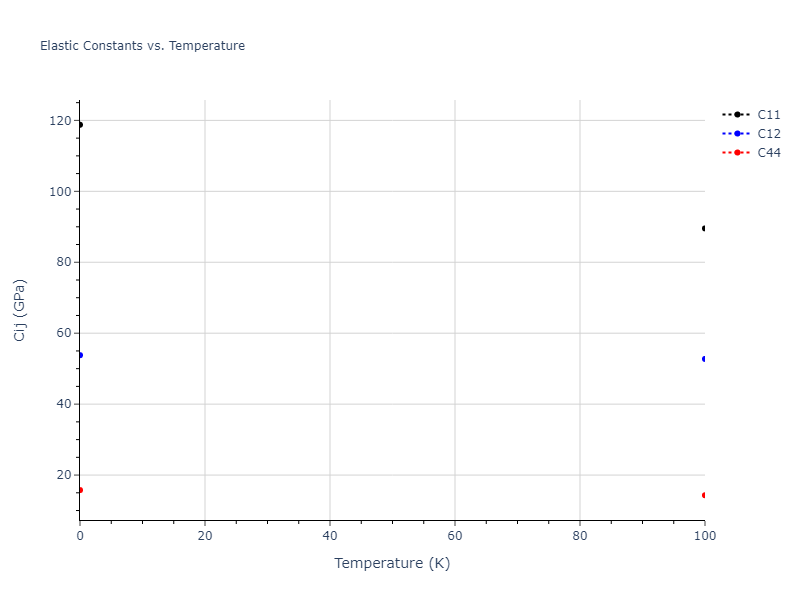
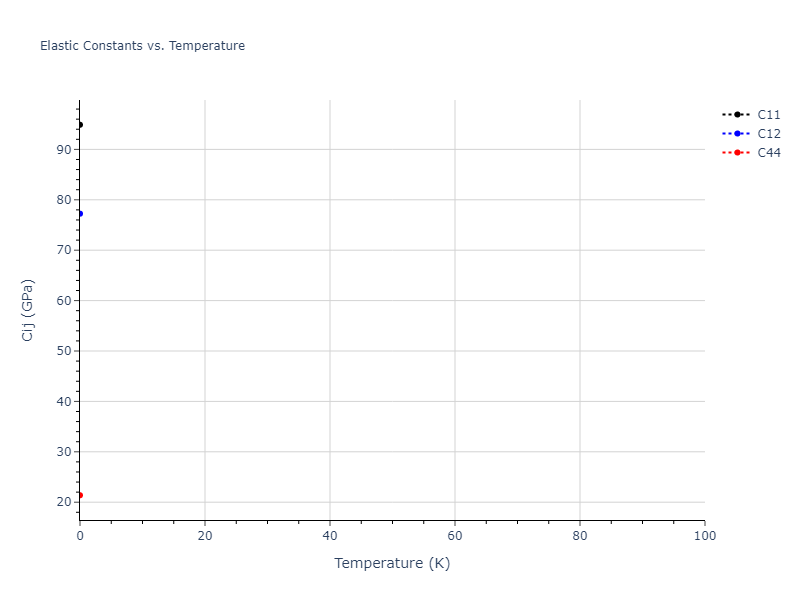
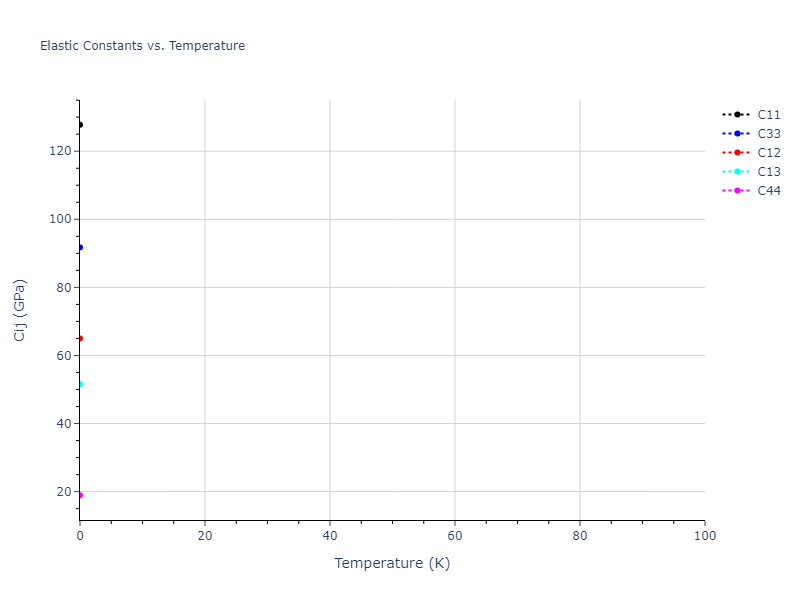
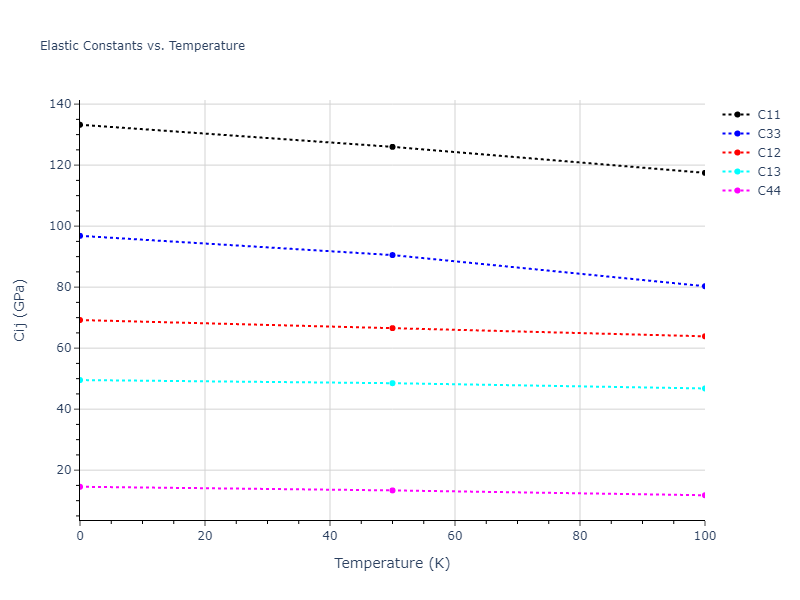
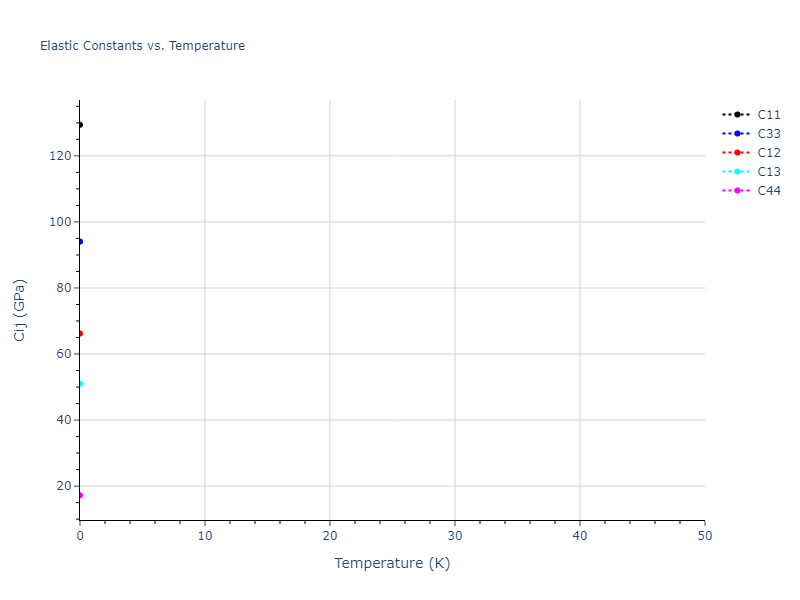
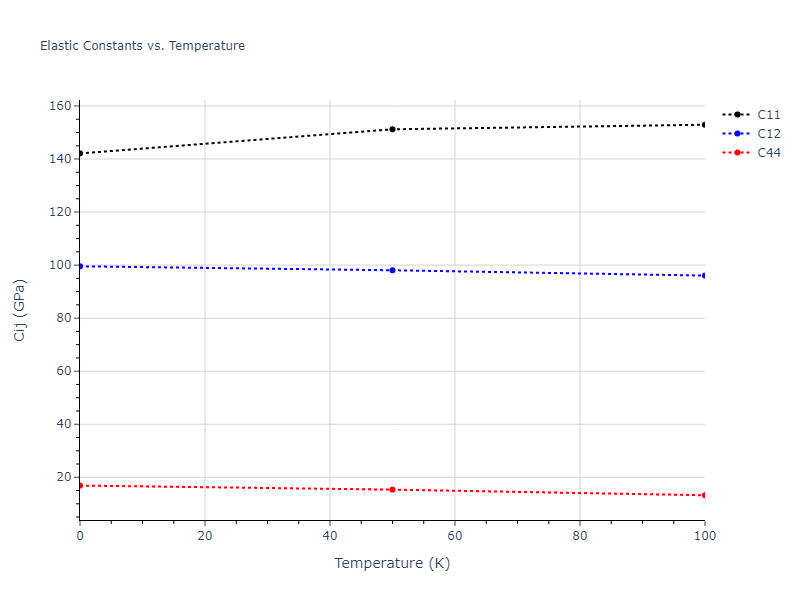
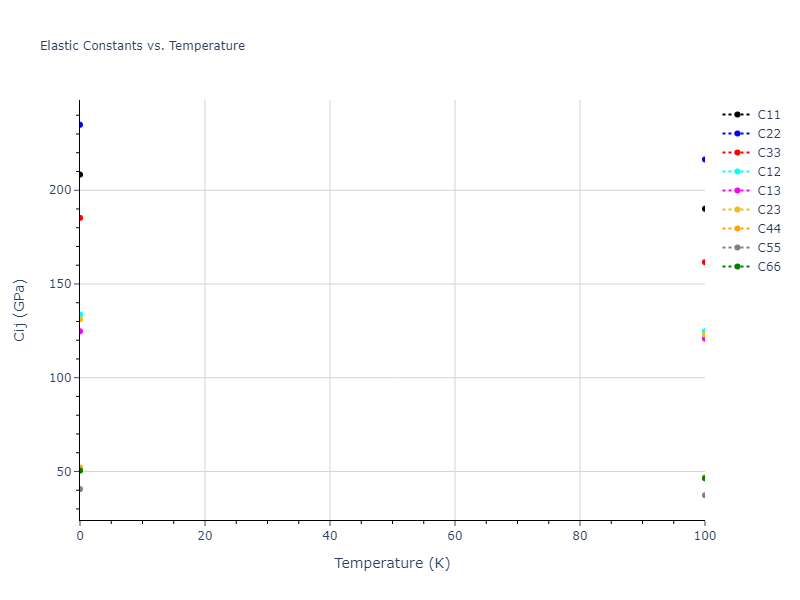
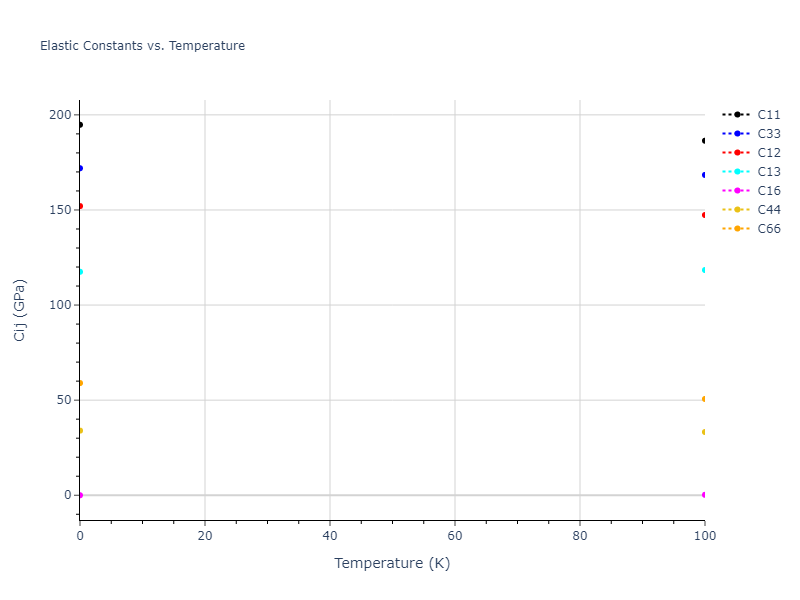
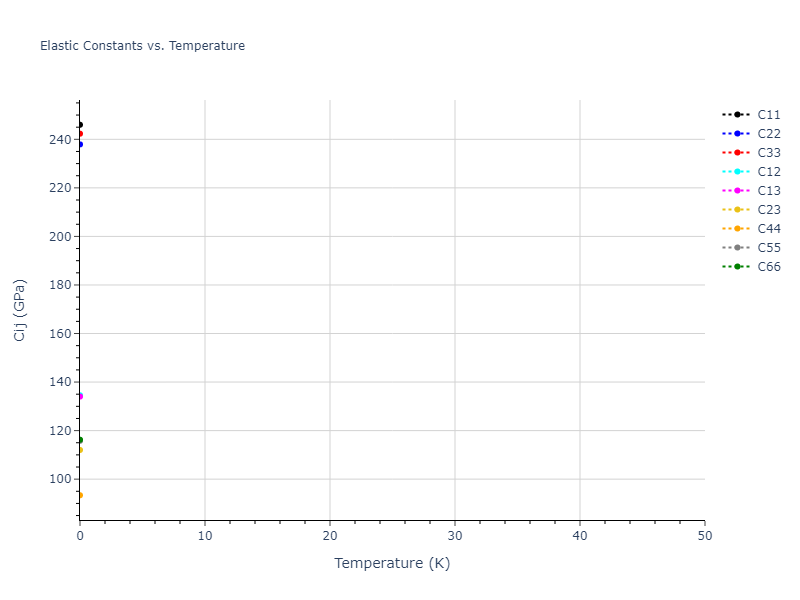
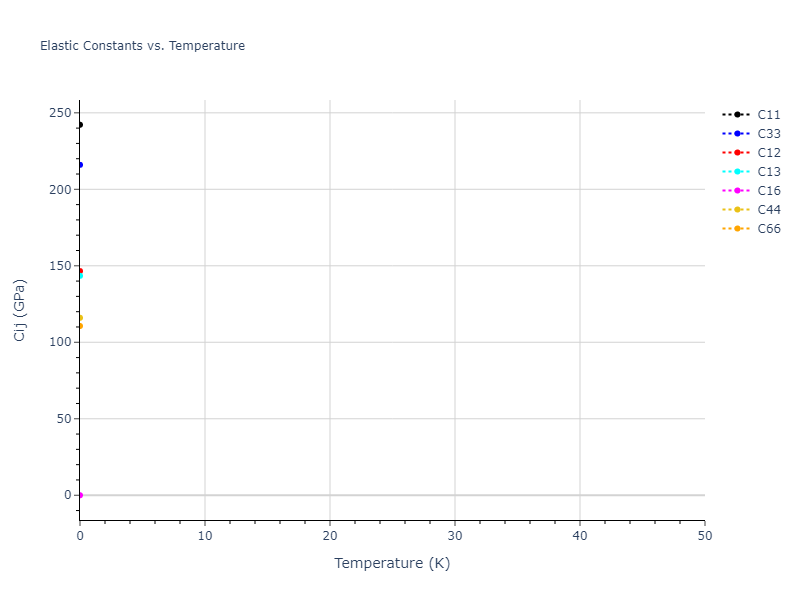
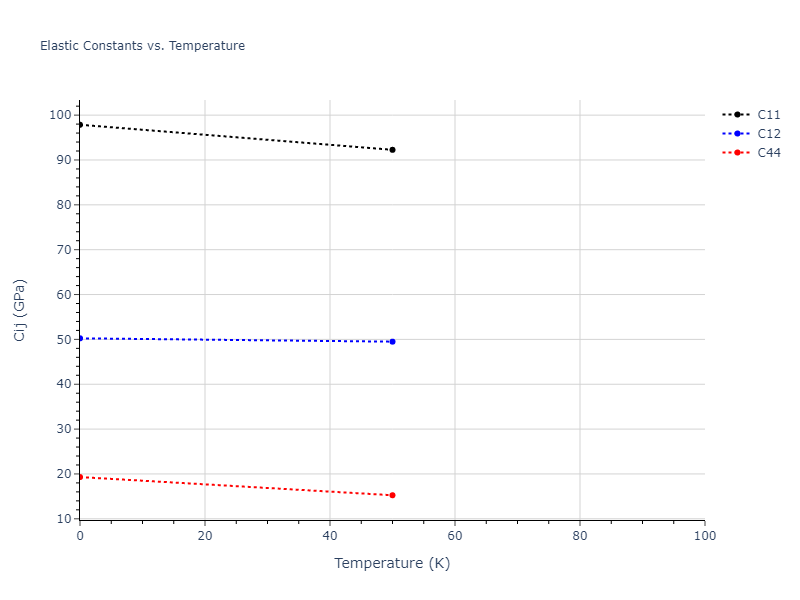
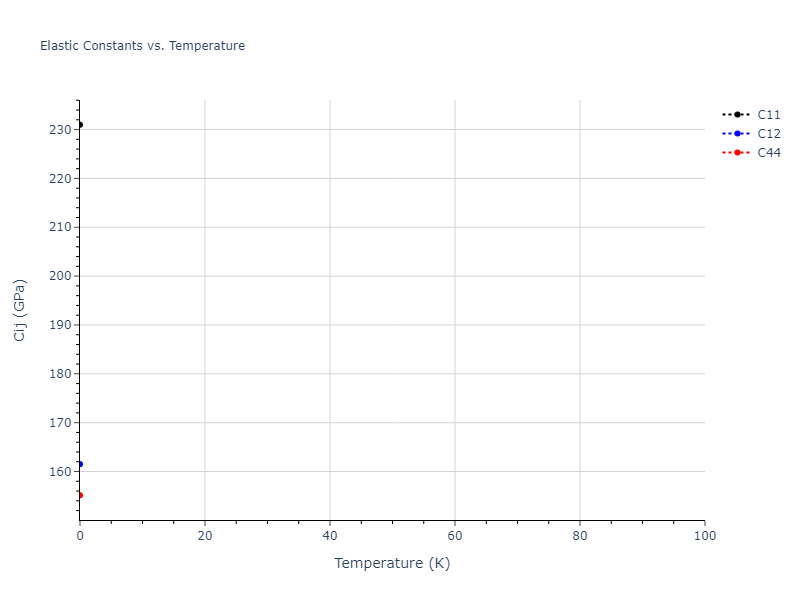
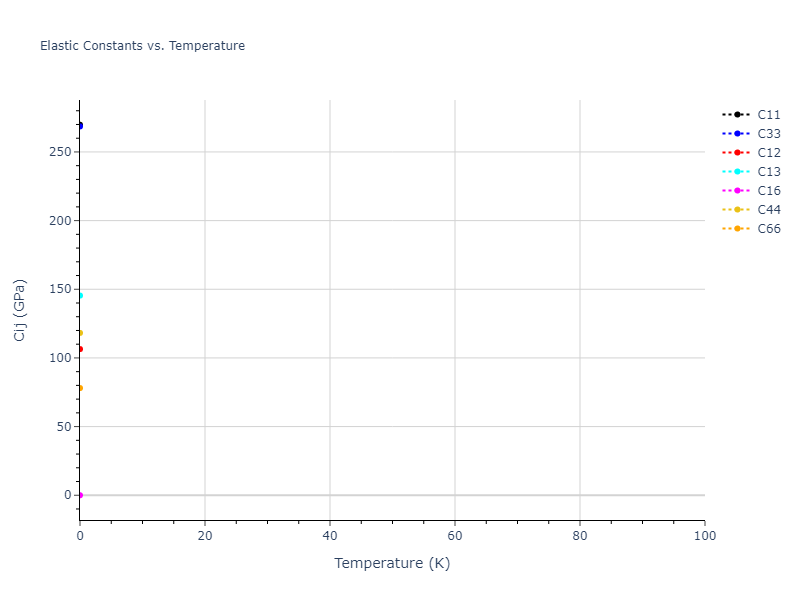
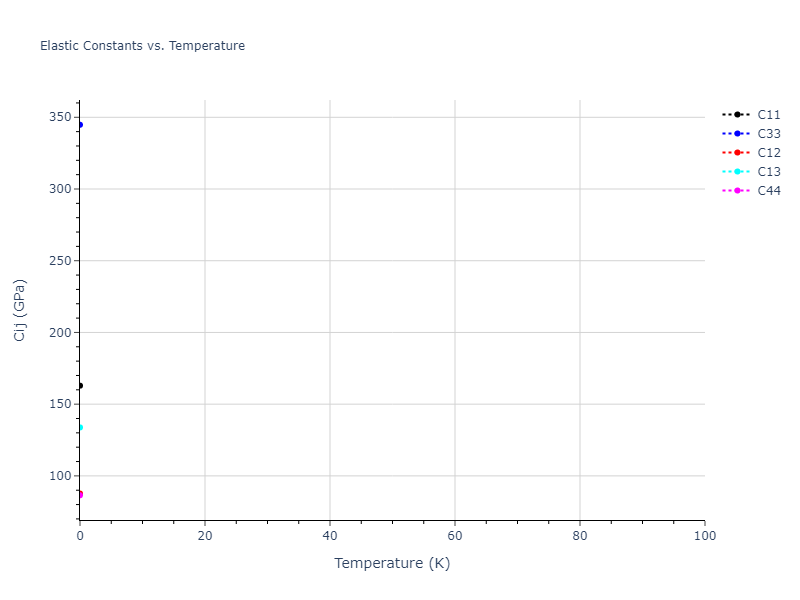
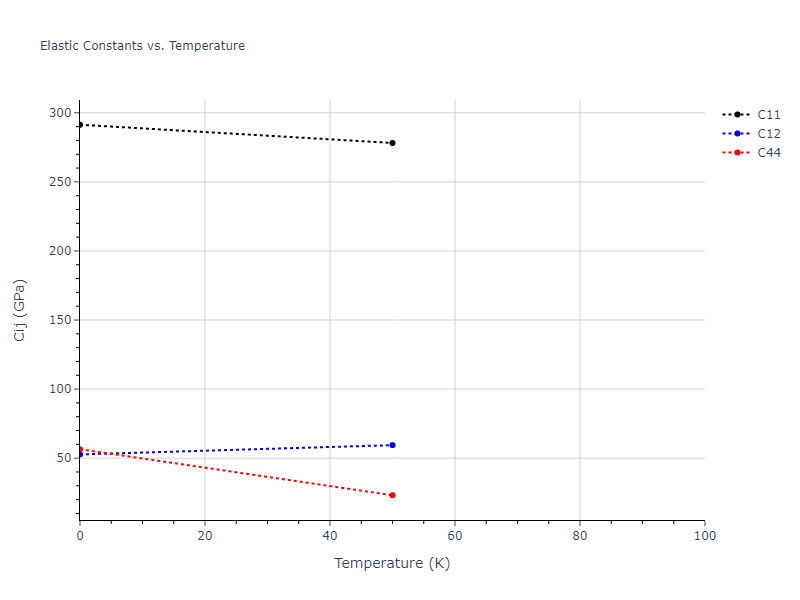
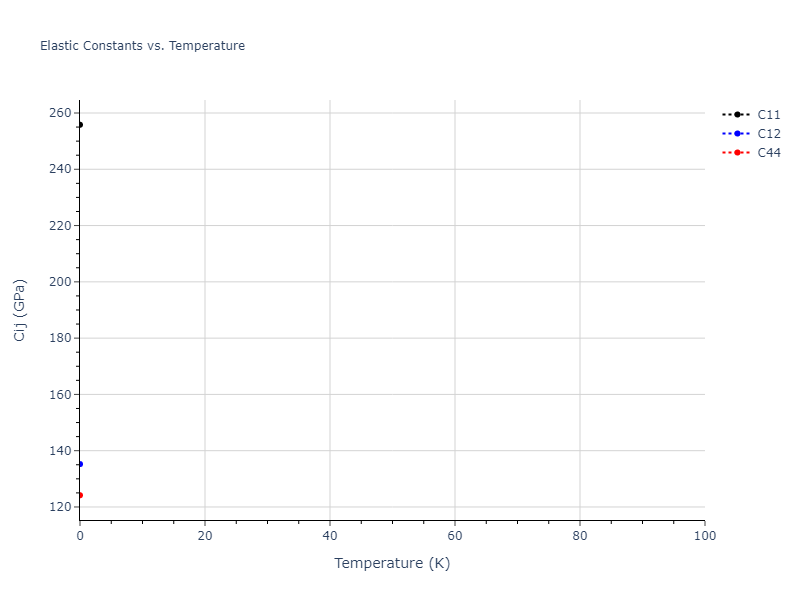
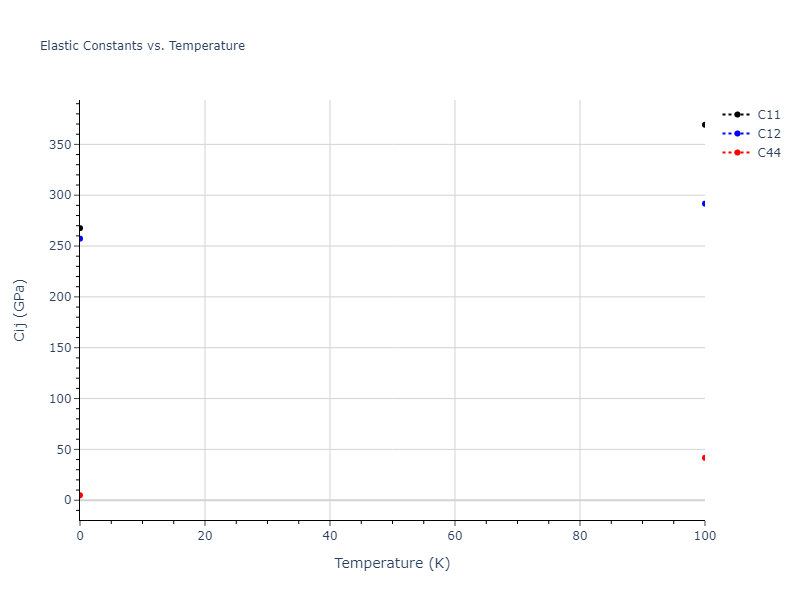
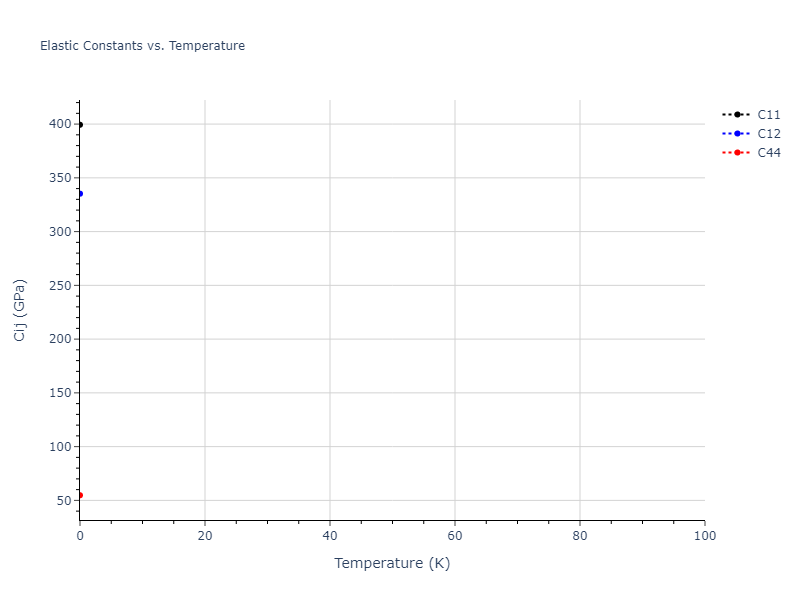
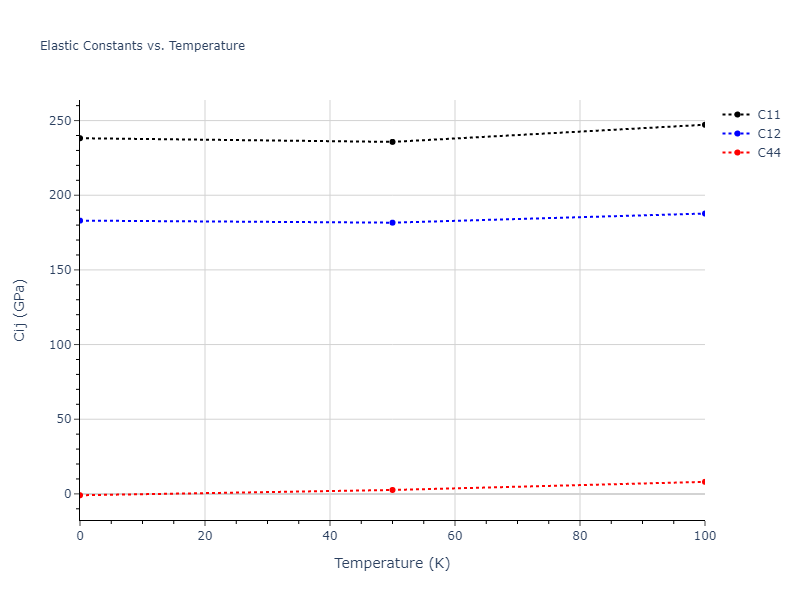
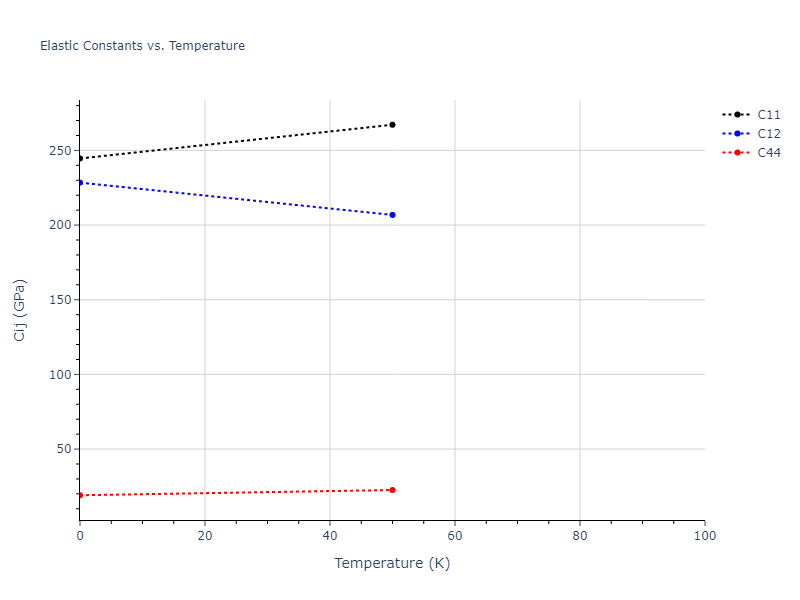
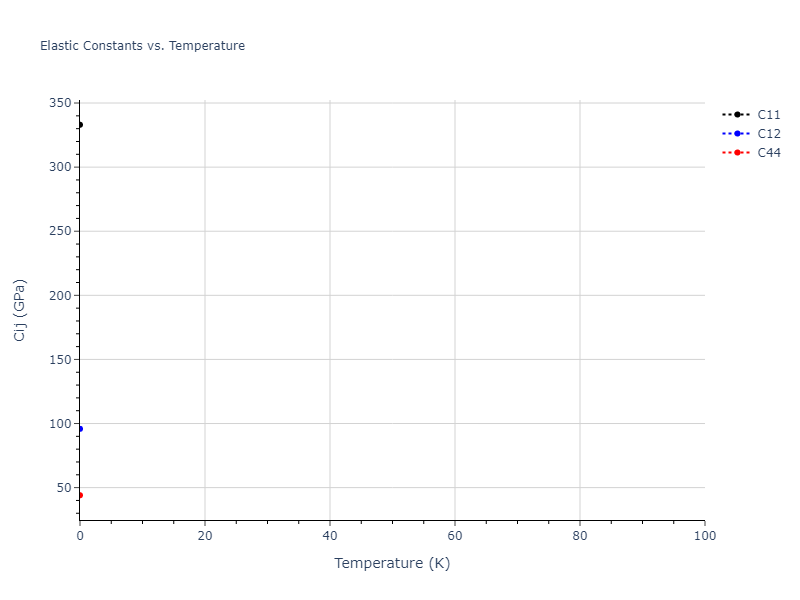
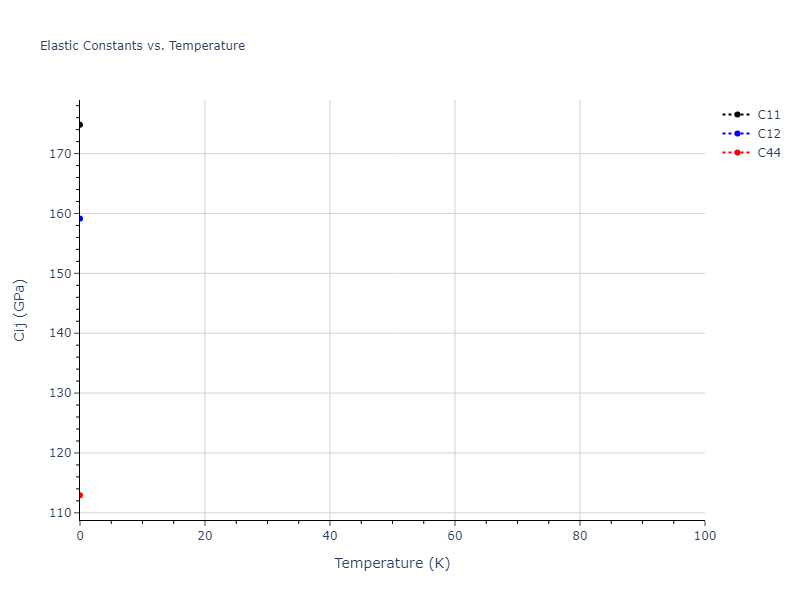
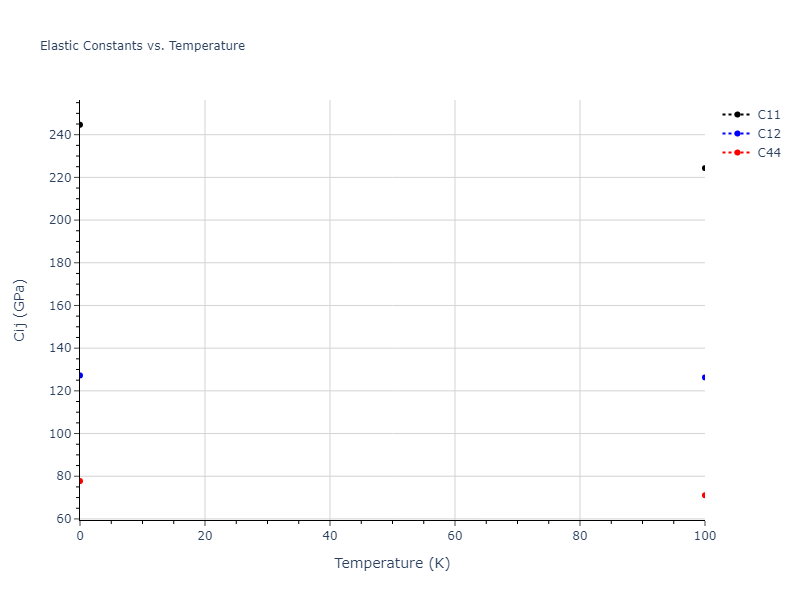
Elastic Constants Predictions
Static elastic constants are displayed for the unique structures identified in Crystal Structure Predictions above. The values displayed here are obtained by measuring the change in virial stresses due to applying small strains to the relaxed crystals. The initial structure and the strained states are all relaxed using force minimization.
The calculation method used is available as the iprPy elastic_constants_static calculation method.
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for variations in calculation methods, simulation software and implementations of the interatomic potentials.
- The presence of any structures in this list does not guarantee that those structures are stable.
- The elastic constants have been computed for a variety of strains, and in some cases for slightly different lattice constant values. The static nature of this calculation can give poor predictions if the evaluated states straddle a functional discontinuity in the potential's third derivative. Be sure to compare the elastic constants for the different strains (positive and negative).
- NIST disclaimer
Version Information:
- 2019-08-07. Data added.
| 114.016 | 62.046 | 62.046 | 0.000 | -0.000 | -0.000 |
| 62.046 | 114.016 | 62.046 | 0.000 | -0.000 | 0.000 |
| 62.046 | 62.046 | 114.016 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 31.616 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 31.616 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 31.616 |
| 114.016 | 62.046 | 62.046 | 0.000 | 0.000 | 0.000 |
| 62.046 | 114.016 | 62.046 | -0.000 | 0.000 | 0.000 |
| 62.046 | 62.046 | 114.016 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 31.616 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 31.616 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 31.616 |
| 114.016 | 62.046 | 62.046 | -0.000 | -0.000 | 0.000 |
| 62.046 | 114.016 | 62.046 | 0.000 | -0.000 | 0.000 |
| 62.046 | 62.046 | 114.016 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 31.616 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 31.616 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 31.616 |
| 114.016 | 62.046 | 62.046 | -0.000 | 0.000 | 0.000 |
| 62.046 | 114.016 | 62.046 | -0.000 | 0.000 | -0.000 |
| 62.046 | 62.046 | 114.016 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 31.616 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 31.616 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 31.616 |
| 114.017 | 62.046 | 62.046 | 0.000 | -0.000 | -0.000 |
| 62.046 | 114.017 | 62.046 | 0.000 | 0.000 | 0.000 |
| 62.046 | 62.046 | 114.017 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 31.616 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 31.616 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 31.616 |
| 114.016 | 62.046 | 62.046 | -0.000 | 0.000 | 0.000 |
| 62.046 | 114.016 | 62.046 | 0.000 | 0.000 | -0.000 |
| 62.046 | 62.046 | 114.016 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 31.616 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 31.616 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 31.616 |
| 118.894 | 53.743 | 53.743 | 0.000 | -0.000 | 0.000 |
| 53.743 | 118.894 | 53.743 | -0.000 | 0.000 | 0.000 |
| 53.743 | 53.743 | 118.894 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 15.765 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 15.765 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 15.765 |
| 118.648 | 53.866 | 53.866 | -0.000 | 0.000 | -0.000 |
| 53.866 | 118.648 | 53.866 | -0.000 | -0.000 | -0.000 |
| 53.866 | 53.866 | 118.648 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 15.765 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 15.765 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 15.765 |
| 118.894 | 53.743 | 53.743 | 0.000 | -0.000 | 0.000 |
| 53.743 | 118.894 | 53.743 | 0.000 | -0.000 | 0.000 |
| 53.743 | 53.743 | 118.894 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 15.765 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 15.765 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 15.765 |
| 118.648 | 53.866 | 53.866 | -0.000 | -0.000 | -0.000 |
| 53.866 | 118.648 | 53.866 | 0.000 | 0.000 | -0.000 |
| 53.866 | 53.866 | 118.648 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 15.765 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 15.765 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 15.765 |
| 118.649 | 53.866 | 53.866 | 0.000 | 0.000 | 0.000 |
| 53.866 | 118.649 | 53.866 | 0.000 | 0.000 | 0.000 |
| 53.866 | 53.866 | 118.649 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 15.765 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 15.765 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 15.765 |
| 118.894 | 53.743 | 53.743 | -0.000 | -0.000 | -0.000 |
| 53.743 | 118.894 | 53.743 | -0.000 | 0.000 | -0.000 |
| 53.743 | 53.743 | 118.894 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 15.765 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 15.765 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 15.765 |
| 94.891 | 77.244 | 77.244 | 0.000 | -0.000 | 0.000 |
| 77.244 | 94.891 | 77.244 | 0.000 | -0.000 | 0.000 |
| 77.244 | 77.244 | 94.891 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 21.381 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 21.381 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 21.381 |
| 94.891 | 77.244 | 77.244 | -0.000 | 0.000 | -0.000 |
| 77.244 | 94.891 | 77.244 | -0.000 | 0.000 | -0.000 |
| 77.244 | 77.244 | 94.891 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 21.381 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 21.381 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 21.381 |
| 94.891 | 77.244 | 77.244 | -0.000 | 0.000 | 0.000 |
| 77.244 | 94.891 | 77.244 | 0.000 | -0.000 | 0.000 |
| 77.244 | 77.244 | 94.891 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 21.381 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 21.381 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 21.381 |
| 94.891 | 77.244 | 77.244 | -0.000 | 0.000 | -0.000 |
| 77.244 | 94.891 | 77.244 | -0.000 | 0.000 | -0.000 |
| 77.244 | 77.244 | 94.891 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 21.381 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 21.381 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 21.381 |
| 94.891 | 77.244 | 77.244 | 0.000 | 0.000 | 0.000 |
| 77.244 | 94.891 | 77.244 | 0.000 | -0.000 | 0.000 |
| 77.244 | 77.244 | 94.891 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 21.381 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 21.381 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 21.381 |
| 94.891 | 77.244 | 77.244 | -0.000 | -0.000 | -0.000 |
| 77.244 | 94.891 | 77.244 | -0.000 | 0.000 | -0.000 |
| 77.244 | 77.244 | 94.891 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 21.381 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 21.381 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 21.381 |
| 127.769 | 65.001 | 51.591 | 0.000 | -0.000 | -0.000 |
| 65.001 | 127.769 | 51.591 | 0.000 | 0.000 | -0.000 |
| 51.591 | 51.591 | 91.742 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 18.942 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 18.942 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 31.384 |
| 127.769 | 65.001 | 51.591 | -0.000 | -0.000 | 0.000 |
| 65.001 | 127.769 | 51.591 | -0.000 | -0.000 | 0.000 |
| 51.591 | 51.591 | 91.742 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 18.942 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 18.942 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 31.384 |
| 127.769 | 65.001 | 51.591 | 0.000 | 0.000 | -0.000 |
| 65.001 | 127.769 | 51.591 | 0.000 | -0.000 | -0.000 |
| 51.591 | 51.591 | 91.742 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 18.942 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 18.942 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 31.384 |
| 127.769 | 65.001 | 51.591 | -0.000 | -0.000 | 0.000 |
| 65.001 | 127.769 | 51.591 | -0.000 | -0.000 | 0.000 |
| 51.591 | 51.591 | 91.742 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 18.942 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 18.942 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 31.384 |
| 127.770 | 65.001 | 51.591 | 0.000 | 0.000 | -0.000 |
| 65.001 | 127.770 | 51.591 | 0.000 | 0.000 | -0.000 |
| 51.591 | 51.591 | 91.743 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 18.942 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 18.942 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 31.384 |
| 127.768 | 65.001 | 51.591 | -0.000 | -0.000 | 0.000 |
| 65.001 | 127.768 | 51.591 | -0.000 | -0.000 | 0.000 |
| 51.591 | 51.591 | 91.741 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 18.942 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 18.942 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 31.384 |
| 133.168 | 69.253 | 49.541 | 0.000 | 0.000 | 0.000 |
| 68.986 | 133.436 | 49.541 | -0.000 | 0.000 | 0.000 |
| 49.541 | 49.541 | 96.821 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 14.563 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 14.563 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 32.225 |
| 133.168 | 69.253 | 49.541 | 0.000 | -0.000 | -0.000 |
| 68.986 | 133.436 | 49.541 | 0.000 | -0.000 | -0.000 |
| 49.541 | 49.541 | 96.821 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 14.563 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 14.563 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 32.225 |
| 133.169 | 69.253 | 49.541 | -0.000 | 0.000 | 0.000 |
| 68.986 | 133.436 | 49.541 | -0.000 | 0.000 | 0.000 |
| 49.541 | 49.541 | 96.821 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 14.563 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 14.563 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 31.958 |
| 133.168 | 69.253 | 49.541 | 0.000 | -0.000 | -0.000 |
| 69.253 | 133.168 | 49.541 | -0.000 | -0.000 | -0.000 |
| 49.541 | 49.541 | 96.821 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 14.563 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 14.563 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 31.958 |
| 133.437 | 68.986 | 49.541 | -0.000 | -0.000 | 0.000 |
| 69.330 | 133.092 | 49.541 | 0.000 | 0.000 | 0.000 |
| 49.541 | 49.541 | 96.821 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 14.563 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 14.563 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 32.225 |
| 133.168 | 69.253 | 49.541 | -0.000 | -0.000 | -0.000 |
| 68.986 | 133.435 | 49.541 | 0.000 | -0.000 | -0.000 |
| 49.541 | 49.541 | 96.821 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 14.563 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 14.563 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 32.225 |
| 133.428 | 137.336 | 137.336 | 0.000 | 0.000 | 0.000 |
| 137.336 | 133.428 | 137.336 | 0.000 | 0.000 | 0.000 |
| 137.336 | 137.336 | 133.428 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 50.044 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 50.044 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 50.044 |
| 133.428 | 137.336 | 137.336 | -0.000 | -0.000 | -0.000 |
| 137.336 | 133.428 | 137.336 | -0.000 | -0.000 | -0.000 |
| 137.336 | 137.336 | 133.428 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 50.044 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 50.044 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 50.044 |
| 133.428 | 137.336 | 137.336 | 0.000 | 0.000 | 0.000 |
| 137.336 | 133.428 | 137.336 | 0.000 | 0.000 | -0.000 |
| 137.336 | 137.336 | 133.428 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -16.894 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -16.894 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -16.894 |
| 133.428 | 137.336 | 137.336 | -0.000 | -0.000 | -0.000 |
| 137.336 | 133.428 | 137.336 | -0.000 | -0.000 | -0.000 |
| 137.336 | 137.336 | 133.428 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -16.894 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -16.894 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -16.894 |
| 133.428 | 137.336 | 137.336 | 0.000 | 0.000 | 0.000 |
| 137.336 | 133.428 | 137.336 | 0.000 | 0.000 | 0.000 |
| 137.336 | 137.336 | 133.428 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -16.894 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -16.894 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -16.894 |
| 133.428 | 137.336 | 137.336 | -0.000 | 0.000 | -0.000 |
| 137.336 | 133.428 | 137.336 | -0.000 | 0.000 | 0.000 |
| 137.336 | 137.336 | 133.428 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -16.894 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -16.894 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -16.894 |
| 105.968 | 106.152 | 81.595 | -0.000 | -0.000 | 0.000 |
| 106.152 | 105.968 | 81.595 | -0.000 | -0.000 | -0.000 |
| 81.595 | 81.595 | 128.027 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 8.876 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 8.876 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 8.487 |
| 133.533 | 78.587 | 81.595 | 0.000 | 0.000 | 0.000 |
| 78.587 | 133.533 | 81.595 | 0.000 | 0.000 | 0.000 |
| 81.595 | 81.595 | 128.027 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 8.876 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 8.876 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 8.487 |
| 133.533 | 78.587 | 81.595 | -0.000 | -0.000 | -0.000 |
| 78.587 | 133.533 | 81.595 | -0.000 | -0.000 | -0.000 |
| 81.595 | 81.595 | 128.027 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 8.876 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 8.876 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 8.487 |
| 105.968 | 106.152 | 81.595 | 0.000 | 0.000 | -0.000 |
| 106.152 | 105.968 | 81.595 | 0.000 | 0.000 | 0.000 |
| 81.595 | 81.595 | 128.027 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 8.876 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 8.876 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 8.487 |
| 105.968 | 106.152 | 81.595 | -0.000 | -0.000 | -0.000 |
| 106.152 | 105.968 | 81.595 | -0.000 | -0.000 | -0.000 |
| 81.595 | 81.595 | 128.027 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 8.876 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 8.876 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 8.487 |
| 105.968 | 106.152 | 81.595 | 0.000 | 0.000 | 0.000 |
| 106.152 | 105.968 | 81.595 | 0.000 | 0.000 | 0.000 |
| 81.595 | 81.595 | 128.026 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 8.876 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 8.876 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 8.487 |
| 118.055 | 70.501 | 70.501 | -0.000 | -0.000 | 0.000 |
| 70.501 | 118.055 | 70.501 | -0.000 | -0.000 | -0.000 |
| 70.501 | 70.501 | 118.055 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 5.318 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 5.318 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 5.318 |
| 118.055 | 70.501 | 70.501 | 0.000 | 0.000 | 0.000 |
| 70.501 | 118.055 | 70.501 | 0.000 | 0.000 | -0.000 |
| 70.501 | 70.501 | 118.055 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 5.318 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 5.318 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 5.318 |
| 118.055 | 70.501 | 70.501 | -0.000 | -0.000 | 0.000 |
| 70.501 | 118.055 | 70.501 | -0.000 | -0.000 | 0.000 |
| 70.501 | 70.501 | 118.055 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 5.318 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 5.318 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 5.318 |
| 118.055 | 70.501 | 70.501 | 0.000 | 0.000 | -0.000 |
| 70.501 | 118.055 | 70.501 | 0.000 | 0.000 | 0.000 |
| 70.501 | 70.501 | 118.055 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 5.318 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 5.318 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 5.318 |
| 118.056 | 70.501 | 70.501 | -0.000 | -0.000 | 0.000 |
| 70.501 | 118.056 | 70.501 | -0.000 | -0.000 | 0.000 |
| 70.501 | 70.501 | 118.056 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 5.318 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 5.318 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 5.318 |
| 118.054 | 70.501 | 70.501 | 0.000 | 0.000 | 0.000 |
| 70.501 | 118.054 | 70.501 | 0.000 | 0.000 | -0.000 |
| 70.501 | 70.501 | 118.054 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 5.318 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 5.318 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 5.318 |
| 101.175 | 65.552 | 94.026 | -0.000 | 0.000 | 0.000 |
| 65.552 | 101.175 | 94.026 | -0.000 | -0.000 | 0.000 |
| 97.960 | 97.960 | 206.190 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 22.209 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 22.209 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 16.729 |
| 87.579 | 62.947 | 103.339 | 0.000 | 0.000 | -0.000 |
| 62.947 | 87.579 | 103.339 | 0.000 | 0.000 | -0.000 |
| 97.960 | 97.960 | 206.190 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 22.209 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 22.209 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 16.729 |
| 61.970 | 94.430 | 99.962 | -0.000 | -0.000 | 0.000 |
| 94.430 | 61.970 | 99.962 | -0.000 | -0.000 | 0.000 |
| 92.024 | 92.024 | 213.013 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 22.209 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 22.209 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 16.729 |
| 61.970 | 94.430 | 99.962 | 0.000 | 0.000 | -0.000 |
| 94.430 | 61.970 | 99.962 | 0.000 | 0.000 | -0.000 |
| 92.024 | 92.024 | 213.013 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 22.209 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 22.209 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 16.729 |
| 61.970 | 94.431 | 99.962 | 0.000 | -0.000 | 0.000 |
| 94.431 | 61.970 | 99.962 | -0.000 | -0.000 | 0.000 |
| 97.960 | 97.960 | 206.190 | -0.000 | -0.000 | 0.000 |
| 0.002 | 0.002 | -0.003 | -42.272 | -0.000 | 0.000 |
| 0.002 | 0.002 | -0.003 | -0.000 | -42.272 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 16.729 |
| 61.969 | 94.430 | 99.962 | 0.000 | 0.000 | -0.000 |
| 94.430 | 61.969 | 99.962 | 0.000 | 0.000 | -0.000 |
| 97.959 | 97.959 | 206.190 | 0.000 | 0.000 | -0.000 |
| -0.002 | -0.002 | 0.003 | -42.272 | 0.000 | -0.000 |
| -0.002 | -0.002 | 0.003 | 0.000 | -42.272 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 16.729 |
| 390.190 | -87.539 | 60.430 | -232.439 | -67.453 | -16.497 |
| 59.373 | 92.266 | 59.655 | -1.179 | 0.228 | -0.505 |
| 543.355 | -266.174 | 175.330 | -244.912 | -21.596 | -8.877 |
| 485.439 | -308.357 | 69.884 | -299.056 | 73.234 | -5.884 |
| 77.084 | -117.908 | 36.759 | -108.269 | 1.959 | -21.603 |
| 483.812 | -309.062 | 69.842 | -308.471 | 71.373 | 3.686 |
| -231.065 | 206.168 | 60.626 | 232.922 | 64.676 | 13.601 |
| -18.542 | 202.978 | 22.727 | 106.591 | 11.920 | 20.773 |
| 60.284 | 59.691 | 93.845 | 0.370 | -1.254 | -0.313 |
| -78.189 | 117.801 | -37.884 | 121.092 | 11.575 | 21.224 |
| -311.748 | 146.749 | -1.230 | 232.477 | 76.641 | 14.655 |
| -311.937 | 146.061 | -0.552 | 232.610 | 64.624 | 25.491 |
| 110.623 | 44.641 | 60.524 | -23.018 | -7.995 | -2.953 |
| 97.916 | 50.168 | 73.575 | -22.326 | -1.315 | -5.828 |
| 60.284 | 59.691 | 93.845 | 0.370 | -1.254 | -0.313 |
| 31.304 | -15.019 | -0.097 | -12.812 | -6.906 | -1.603 |
| -1.320 | 0.186 | -1.254 | -0.409 | 17.184 | -0.530 |
| 37.781 | -25.106 | 12.467 | -21.166 | -2.828 | 5.108 |
| 78.097 | 71.733 | 57.496 | 11.042 | -0.620 | 0.653 |
| 9.977 | 102.483 | 53.875 | 29.207 | -7.318 | -0.690 |
| 10.612 | 91.609 | 70.356 | 30.733 | -8.947 | 0.324 |
| -0.270 | 0.485 | 0.370 | 16.682 | -0.409 | 0.186 |
| -32.175 | 14.575 | -1.319 | 23.060 | 17.161 | 1.111 |
| -1.053 | -0.505 | -0.187 | 0.228 | -2.242 | 16.296 |
| 79.605 | 54.319 | 59.577 | -3.205 | -2.189 | -2.411 |
| 60.627 | 83.876 | 61.208 | -2.453 | -0.100 | -0.589 |
| 63.469 | 58.404 | 80.411 | -2.094 | -1.617 | -0.922 |
| 4.400 | -3.615 | 0.685 | 6.032 | 0.790 | -0.576 |
| -0.484 | -1.229 | -0.945 | -1.426 | 13.646 | -0.670 |
| 2.236 | -3.541 | 0.933 | -2.405 | -1.712 | 9.420 |
| 70.552 | 60.889 | 57.827 | 1.761 | -1.783 | -2.152 |
| 54.838 | 77.194 | 59.514 | 0.486 | 0.049 | -0.694 |
| 60.481 | 61.963 | 86.920 | 1.253 | -1.216 | -0.297 |
| -5.179 | 2.417 | -0.713 | 11.782 | -0.605 | -0.465 |
| -4.149 | 1.315 | -1.324 | 2.064 | 11.152 | -0.248 |
| -2.054 | 0.826 | -0.762 | 1.206 | -1.710 | 13.286 |
| 91.667 | 58.978 | 60.069 | -0.196 | -3.785 | -0.660 |
| 59.514 | 91.950 | 58.383 | -1.600 | -0.232 | 0.360 |
| 60.330 | 58.092 | 93.843 | -0.384 | -0.245 | 0.434 |
| -0.218 | -0.958 | -0.384 | 16.474 | 0.159 | -0.287 |
| -1.179 | -0.291 | -0.245 | 0.159 | 18.080 | -0.151 |
| 0.203 | 0.360 | 0.402 | -0.227 | -0.933 | 17.875 |
| 91.667 | 58.978 | 60.069 | -0.196 | -3.785 | -0.659 |
| 92.796 | -55.573 | -143.901 | -42.769 | 77.477 | 213.446 |
| 60.330 | 58.092 | 93.843 | -0.384 | -0.245 | 0.434 |
| 23.436 | -126.802 | -281.385 | -45.371 | 67.367 | 230.341 |
| -1.179 | -0.291 | -0.245 | 0.159 | 18.080 | -0.151 |
| 0.203 | 0.360 | 0.402 | -0.227 | -0.933 | 17.875 |
| 91.667 | 58.978 | 60.069 | -0.196 | -3.785 | -0.659 |
| 62.981 | 86.159 | 52.575 | -1.690 | -0.958 | -7.056 |
| 60.330 | 58.092 | 93.843 | -0.384 | -0.245 | 0.434 |
| -0.218 | -0.958 | -0.384 | 16.474 | 0.159 | -0.287 |
| -1.179 | -0.291 | -0.245 | 0.159 | 18.080 | -0.151 |
| 3.848 | 5.343 | -5.705 | 0.050 | -1.705 | 4.265 |
| 64.797 | 51.852 | 57.463 | 1.585 | 5.069 | 12.863 |
| 60.205 | 50.980 | 46.515 | -4.330 | 8.832 | 15.475 |
| 58.463 | 56.718 | 89.199 | -1.103 | -0.134 | 4.542 |
| 0.528 | -7.799 | -5.318 | 6.372 | 6.400 | 11.425 |
| -1.484 | -6.672 | -3.793 | -0.222 | 13.376 | 11.235 |
| 0.203 | 0.360 | 0.402 | -0.227 | -0.933 | 17.875 |
| 70.157 | 58.372 | 60.408 | 1.425 | -2.132 | 0.039 |
| 60.177 | 81.237 | 57.573 | -1.884 | -0.204 | -0.359 |
| 59.673 | 57.524 | 76.465 | -1.046 | -0.237 | -0.816 |
| 1.022 | -1.216 | -0.840 | 13.358 | 0.086 | -0.755 |
| -0.428 | 1.005 | 0.515 | 0.438 | 7.522 | -1.333 |
| 0.822 | 0.676 | -0.274 | -0.145 | -0.907 | 13.772 |
| 83.931 | 59.515 | 61.668 | 0.719 | -3.104 | 0.427 |
| 59.457 | 79.751 | 58.646 | -1.876 | -0.033 | 1.162 |
| 57.522 | 53.324 | 69.035 | -1.041 | 1.862 | 3.764 |
| -0.218 | -0.958 | -0.384 | 16.474 | 0.159 | -0.287 |
| -1.271 | -0.661 | -0.129 | 0.100 | 11.936 | 0.321 |
| 1.749 | -0.752 | -0.148 | -0.416 | 0.015 | 10.696 |
| 740227.072 | 8476117.160 | -1203921.888 | 646362.451 | 2037550.097 | 281449.884 |
| 706471.854 | 8485069.737 | -1221323.763 | 654677.332 | 2070719.489 | 254650.497 |
| 997213.433 | 8629736.434 | -1241405.331 | 747341.862 | 2092203.752 | 290399.450 |
| 874532.918 | 8326218.831 | -1221231.640 | 678842.884 | 2112987.289 | 209568.592 |
| 742232.170 | 8523628.086 | -1201720.727 | 648675.774 | 2036866.229 | 273793.234 |
| 695740.923 | 8249548.587 | -1240870.895 | 624492.249 | 2060541.572 | 240701.709 |
| -884271.262 | -8526835.827 | 1152539.959 | -633537.556 | -2097208.713 | -307239.123 |
| -962430.780 | -8584169.117 | 1258648.773 | -733095.228 | -2040831.255 | -301958.543 |
| -911071.068 | -8430234.019 | 1253756.492 | -701362.023 | -2157340.982 | -244346.934 |
| -691731.020 | -8448426.143 | 1186543.116 | -741774.666 | -2094689.351 | -217588.311 |
| -987687.145 | -8445700.250 | 1189027.961 | -615307.769 | -2165408.285 | -252629.969 |
| -916646.668 | -8581262.400 | 1236908.299 | -678684.542 | -2125372.175 | -262264.727 |
| 73326.381 | 831348.789 | -126476.836 | 64443.046 | 212288.431 | 22675.984 |
| 68254.080 | 850924.581 | -124750.475 | 74191.068 | 208144.815 | 21604.450 |
| 96300.803 | 838903.732 | -116545.692 | 64158.402 | 213699.661 | 23748.198 |
| 76155.488 | 850614.816 | -121949.753 | 66469.678 | 206251.609 | 31078.390 |
| 69399.382 | 845456.869 | -116319.808 | 59259.944 | 205092.172 | 29453.851 |
| 77913.477 | 832239.821 | -120833.523 | 72152.477 | 209618.760 | 32858.528 |
| -76992.696 | -828687.185 | 131103.293 | -67208.330 | -213310.201 | -19266.947 |
| -75025.022 | -832447.911 | 121996.476 | -66223.786 | -211540.039 | -19960.179 |
| -73814.792 | -851376.440 | 115427.477 | -64543.713 | -205802.029 | -29891.328 |
| -95874.371 | -859397.584 | 123584.474 | -73840.107 | -206721.060 | -28792.695 |
| -99750.935 | -865214.081 | 123447.646 | -72615.277 | -204745.412 | -30060.175 |
| -89121.664 | -851536.856 | 124182.771 | -68583.656 | -204367.876 | -25649.313 |
| 7910.761 | 86672.597 | -11673.851 | 6064.285 | 20506.053 | 3107.213 |
| 8270.521 | 84690.705 | -11112.777 | 5861.196 | 20385.044 | 1643.247 |
| 7293.265 | 84318.393 | -10624.946 | 6005.518 | 19643.659 | 2090.715 |
| 6754.363 | 82689.032 | -11557.060 | 7518.798 | 19137.004 | 2209.097 |
| 7627.136 | 85021.854 | -11458.137 | 6254.910 | 20504.859 | 1339.811 |
| 7925.308 | 84422.082 | -11523.381 | 6935.518 | 19884.556 | 2722.989 |
| -6823.120 | -82059.084 | 12254.413 | -7262.859 | -19148.247 | -3230.306 |
| -5339.531 | -82070.000 | 11936.602 | -6514.577 | -20366.779 | -3142.946 |
| -8274.450 | -84125.118 | 11450.653 | -6897.093 | -21522.450 | -1170.117 |
| -6568.135 | -85006.416 | 11504.818 | -5668.942 | -20313.658 | -3123.228 |
| -7471.781 | -83842.637 | 12370.340 | -7014.854 | -20217.223 | -2285.492 |
| -6624.151 | -85050.658 | 11307.301 | -5803.334 | -20159.922 | -2662.976 |
| 94.017 | 76.218 | 46.179 | 13.443 | -39.281 | -4.815 |
| 67.966 | 103.805 | 46.267 | 16.959 | -41.101 | -4.558 |
| 68.512 | 76.654 | 74.100 | 14.472 | -40.664 | -6.313 |
| 7.494 | 17.991 | -13.602 | 28.029 | -41.191 | -5.192 |
| 40.015 | 1.832 | -93.815 | 58.937 | -92.620 | -9.454 |
| 8.769 | 17.781 | -14.012 | 14.767 | -41.185 | 8.048 |
| 91.332 | 59.320 | 58.877 | -0.448 | 2.120 | 1.011 |
| 59.143 | 93.290 | 59.519 | 2.997 | 0.523 | 0.668 |
| 51.217 | 43.336 | 101.466 | -14.299 | 41.951 | 5.111 |
| -9.798 | -15.325 | 13.748 | -0.742 | 41.422 | 6.231 |
| -6.982 | -16.324 | 14.360 | -14.271 | 54.589 | 4.904 |
| -8.522 | -15.534 | 13.337 | -14.004 | 41.429 | 19.463 |
| 91.332 | 59.320 | 58.877 | -0.448 | 2.120 | 1.011 |
| 59.143 | 93.290 | 59.519 | 2.997 | 0.523 | 0.668 |
| 60.745 | 61.670 | 86.318 | 1.529 | -3.494 | -1.179 |
| -0.286 | 2.998 | -1.294 | 15.092 | -4.013 | -0.050 |
| 2.530 | 1.999 | -0.683 | 1.554 | 9.123 | -1.378 |
| 0.987 | 2.786 | -1.703 | 1.823 | -4.011 | 13.220 |
| 79.460 | 56.955 | 64.121 | -3.925 | 9.367 | -0.954 |
| 58.453 | 85.443 | 61.318 | 1.127 | 4.353 | 1.730 |
| 57.927 | 56.060 | 87.952 | -1.795 | 8.706 | -2.115 |
| -2.017 | -0.332 | 1.440 | 12.199 | 4.244 | 1.090 |
| 0.798 | -1.332 | 2.053 | -1.326 | 17.431 | -0.237 |
| -0.739 | -0.538 | 1.027 | -1.060 | 4.255 | 14.286 |
| 80.656 | 59.965 | 58.652 | -0.946 | 1.067 | 1.024 |
| 59.446 | 86.440 | 59.846 | 2.677 | -0.317 | 1.159 |
| 58.852 | 59.556 | 94.593 | 0.033 | 0.514 | -0.229 |
| -1.537 | 0.399 | 0.095 | 7.613 | -0.489 | 0.810 |
| 1.708 | 0.590 | 0.831 | 0.440 | 10.372 | -0.448 |
| 0.213 | 1.294 | -0.479 | 0.542 | -0.325 | 13.769 |
| 91.331 | 59.320 | 58.877 | -0.448 | 2.120 | 1.011 |
| 59.314 | 81.214 | 59.101 | 2.079 | 0.977 | 0.827 |
| 57.569 | 56.571 | 75.286 | 0.775 | 2.552 | -0.717 |
| -1.559 | 1.002 | 1.287 | 11.574 | 0.909 | 0.628 |
| 1.478 | 0.005 | 1.732 | -0.085 | 11.455 | -0.752 |
| -0.014 | 1.015 | 0.218 | 0.371 | 0.685 | 8.422 |
| 119.777 | 108.881 | 90.851 | 1.640 | -0.452 | 6.935 |
| 61.061 | 97.090 | 62.264 | 2.077 | -0.371 | 1.762 |
| 121.079 | 214.851 | 261.214 | -5.090 | 81.210 | -11.923 |
| 12.080 | 27.782 | 20.588 | 26.898 | -9.053 | 1.041 |
| -1.167 | -0.307 | 0.184 | -0.687 | 18.350 | -0.634 |
| -0.574 | 1.763 | -0.452 | -0.389 | 0.169 | 18.175 |
| 76.182 | 36.111 | 42.442 | -12.416 | 8.271 | 0.390 |
| 49.449 | 64.003 | 43.120 | -9.518 | 7.874 | 0.507 |
| -1.060 | -91.101 | -71.140 | 11.204 | -72.278 | 8.973 |
| -0.600 | 0.995 | 0.528 | 18.799 | -0.687 | -0.325 |
| -1.167 | -0.307 | 0.184 | -0.687 | 18.350 | -0.634 |
| -62.497 | -149.049 | -136.152 | 9.658 | -70.661 | 11.189 |
| 93.959 | 61.416 | 61.589 | -0.547 | -0.394 | 2.055 |
| 61.061 | 97.090 | 62.264 | 2.077 | -0.371 | 1.762 |
| 65.695 | 66.568 | 91.433 | 0.975 | -0.401 | 0.046 |
| 3.607 | 6.375 | 3.686 | 11.531 | -0.486 | 0.553 |
| 4.760 | 11.498 | 9.631 | -0.642 | 9.919 | -2.446 |
| 0.467 | 4.167 | 1.571 | 1.115 | -1.154 | 15.327 |
| 93.959 | 61.416 | 61.589 | -0.547 | -0.394 | 2.055 |
| 60.850 | 87.514 | 60.954 | 1.172 | 0.199 | 1.454 |
| 61.402 | 62.143 | 98.882 | 0.528 | 0.184 | -0.235 |
| -4.179 | -11.462 | -10.701 | -0.862 | -6.172 | 1.239 |
| -4.598 | -5.522 | -3.353 | -0.673 | 12.837 | -1.769 |
| -2.080 | -1.115 | -2.413 | -1.270 | 0.556 | 15.087 |
| 84.009 | 63.030 | 62.586 | -0.041 | -0.410 | 1.383 |
| 62.487 | 89.242 | 63.337 | 2.578 | -0.825 | 1.538 |
| 61.403 | 62.143 | 98.882 | 0.528 | 0.184 | -0.235 |
| 0.246 | 2.098 | 1.081 | 11.794 | -0.554 | -0.003 |
| -0.518 | -0.694 | -0.477 | -0.144 | 11.435 | -1.221 |
| -0.172 | 1.608 | -0.325 | 0.066 | -0.428 | 10.748 |
| 83.231 | 61.912 | 61.869 | 0.074 | -0.506 | 1.384 |
| 61.061 | 97.090 | 62.263 | 2.077 | -0.371 | 1.762 |
| 61.402 | 62.142 | 98.882 | 0.528 | 0.184 | -0.235 |
| -0.538 | 1.229 | 0.543 | 11.977 | -0.528 | -0.072 |
| -1.138 | -1.765 | -1.560 | -0.305 | 11.013 | -1.090 |
| -0.960 | 0.820 | -1.053 | -0.101 | -0.607 | 12.614 |
| -32.265 | 45.768 | 63.132 | 76.038 | 25.433 | -24.693 |
| -56.787 | 74.769 | 63.721 | 74.571 | 24.310 | -23.386 |
| -152.787 | 86.037 | 31.195 | 71.866 | 108.426 | -7.382 |
| -207.875 | 83.951 | -74.492 | 110.482 | 71.110 | 2.989 |
| -116.907 | -16.268 | 4.203 | 75.315 | 36.854 | -23.334 |
| -119.435 | -16.642 | 2.312 | 75.710 | 23.630 | -9.738 |
| 205.385 | 78.259 | 57.419 | -75.689 | -23.250 | 21.308 |
| 274.692 | 58.987 | 105.141 | -75.120 | -106.614 | 6.192 |
| 271.062 | 34.713 | 120.793 | -75.028 | -104.202 | 5.955 |
| 118.881 | 15.369 | -4.541 | -62.392 | -24.828 | 22.843 |
| 120.744 | 16.222 | -1.510 | -76.411 | -11.833 | 22.667 |
| -0.137 | -0.529 | -0.475 | -0.338 | -0.668 | 17.400 |
| 93.968 | 60.708 | 59.299 | -0.187 | 0.671 | -1.545 |
| 41.615 | 87.190 | 55.870 | 5.656 | 10.308 | -1.143 |
| 37.975 | 62.930 | 71.507 | 5.755 | 12.726 | -1.381 |
| -0.240 | -0.666 | -1.154 | 17.134 | -0.394 | -0.350 |
| -20.587 | 2.150 | -2.388 | 7.219 | 20.125 | -1.016 |
| -12.485 | -2.021 | -0.259 | 7.430 | 1.722 | 10.978 |
| 93.968 | 60.707 | 59.299 | -0.187 | 0.671 | -1.545 |
| 73.931 | 92.597 | 60.583 | -8.879 | -2.464 | 1.915 |
| 80.303 | 57.819 | 80.544 | -8.915 | -8.505 | -0.045 |
| 11.937 | 0.750 | -1.967 | 5.908 | -2.921 | 2.141 |
| 20.219 | -8.300 | 9.255 | -10.292 | 0.588 | -1.212 |
| 11.266 | 1.228 | -0.830 | -7.735 | -3.145 | 15.546 |
| 73.231 | 61.511 | 56.268 | 0.325 | 0.349 | -1.728 |
| 60.646 | 97.353 | 60.301 | -1.155 | -0.346 | -0.530 |
| 59.116 | 60.681 | 84.425 | -0.915 | 1.597 | -0.754 |
| -1.098 | -1.051 | -1.693 | 13.966 | -0.253 | -0.372 |
| 1.681 | -0.358 | 1.500 | -0.394 | 16.383 | -0.202 |
| -2.866 | -0.274 | -1.144 | 0.441 | 0.356 | 10.541 |
| 87.535 | 62.218 | 60.277 | -0.583 | 0.859 | -1.464 |
| 60.646 | 97.353 | 60.301 | -1.155 | -0.346 | -0.530 |
| 61.191 | 60.174 | 78.259 | -2.236 | 1.037 | -0.614 |
| 1.865 | -1.508 | -1.170 | 9.664 | -1.186 | -0.189 |
| 1.681 | -0.358 | 1.500 | -0.394 | 16.383 | -0.202 |
| 1.043 | -0.718 | -0.356 | -0.964 | -1.565 | 10.585 |
| -235582.514 | 522173.321 | 718340.477 | -252070.109 | -18675.691 | -40938.533 |
| -214644.728 | 610056.984 | 737378.869 | -275811.664 | -7864.786 | -48098.896 |
| -103646.268 | 544433.832 | 1005275.921 | -250384.182 | -36114.958 | -25019.243 |
| -199183.183 | 502245.943 | 915325.406 | -169501.881 | -26718.007 | -115910.854 |
| -254013.287 | 527182.105 | 854565.752 | -231938.001 | 26125.470 | -72222.727 |
| -255435.724 | 591545.899 | 800220.317 | -245384.978 | 10976.000 | -60571.026 |
| 236737.484 | -505034.683 | -819516.591 | 268929.447 | -17729.052 | 65226.750 |
| 169225.772 | -423744.368 | -642418.395 | 267393.264 | 23250.744 | 31161.823 |
| 292790.532 | -598875.524 | -836099.601 | 303027.478 | -45667.598 | 70361.068 |
| 119860.343 | -554737.874 | -889552.104 | 195521.508 | 35609.212 | 146630.394 |
| 206010.812 | -530899.495 | -727753.219 | 276984.541 | 8161.009 | 51228.052 |
| 237033.252 | -558908.454 | -875994.631 | 321343.711 | -63439.866 | 104892.303 |
| -28424.811 | 65010.212 | 81102.334 | -28582.810 | 6730.333 | -1519.065 |
| -14793.496 | 59409.307 | 75843.460 | -30598.332 | -2707.960 | -3833.026 |
| -8106.609 | 83681.087 | 121322.633 | -36260.525 | -2310.623 | -5395.413 |
| -16171.847 | 46585.840 | 71467.166 | -24101.325 | -874.371 | -7156.245 |
| -20727.698 | 42148.977 | 63361.791 | -25955.931 | -2778.295 | -3896.503 |
| -31867.438 | 44763.862 | 76757.922 | -32824.261 | 1339.563 | -2987.519 |
| 20642.934 | -52671.599 | -78296.909 | 25564.139 | 4258.066 | 1907.680 |
| 19252.202 | -58375.373 | -79002.531 | 28666.549 | 707.561 | 3219.691 |
| 21211.077 | -42518.130 | -64788.578 | 26533.685 | 4848.192 | 4265.322 |
| 14904.771 | -47503.981 | -78389.793 | 28583.696 | 1665.258 | 2580.918 |
| 26950.977 | -53732.450 | -83041.504 | 28476.509 | -833.370 | 4492.582 |
| 30343.060 | -59787.470 | -77350.875 | 29681.563 | -2897.386 | 3050.135 |
| -1495.002 | 5397.369 | 8301.757 | -3059.942 | -540.196 | -1086.188 |
| -1547.376 | 5634.659 | 9277.272 | -2647.564 | -586.425 | -818.675 |
| -2691.021 | 4931.547 | 9382.569 | -3426.709 | -181.998 | -219.365 |
| -716.640 | 5150.332 | 8051.264 | -3302.899 | -713.662 | -648.040 |
| -1970.666 | 5121.044 | 8109.506 | -3180.600 | -267.654 | -326.210 |
| -1663.232 | 5495.165 | 8102.081 | -3171.558 | -224.447 | -1100.374 |
| 935.453 | -5323.734 | -8761.971 | 3463.672 | 490.801 | 334.933 |
| 1544.204 | -4157.861 | -7222.409 | 2327.499 | 140.375 | 652.345 |
| 1599.836 | -5085.739 | -7825.340 | 3241.758 | 480.700 | -113.165 |
| 1241.919 | -5433.167 | -8464.279 | 2997.867 | 564.181 | 255.070 |
| 2869.330 | -5963.984 | -8621.701 | 2605.085 | 104.942 | 404.270 |
| 951.994 | -5310.363 | -8848.776 | 3497.103 | 618.847 | 332.894 |
| 134.242 | 72.755 | 86.612 | -0.000 | 0.000 | -0.000 |
| 92.879 | 133.429 | 95.129 | 0.000 | 0.000 | -0.000 |
| 67.121 | 107.079 | 105.378 | -0.000 | -0.000 | -0.000 |
| -0.731 | 1.300 | -0.520 | 5.392 | -0.000 | -0.000 |
| -2.011 | 4.019 | -1.509 | -0.000 | 28.489 | -0.000 |
| -6.371 | 12.734 | -4.780 | -0.000 | -0.000 | -4.988 |
| 106.557 | 104.566 | 69.926 | 0.000 | -0.000 | 0.000 |
| 70.632 | 173.802 | 79.147 | 0.000 | 0.000 | 0.000 |
| 70.293 | 101.067 | 107.701 | -0.000 | 0.000 | 0.000 |
| 0.731 | -1.300 | 0.520 | 5.392 | 0.000 | 0.000 |
| 2.011 | -4.019 | 1.509 | 0.000 | 28.489 | 0.000 |
| 6.371 | -12.734 | 4.780 | -0.000 | 0.000 | -4.988 |
| 115.604 | 103.015 | 73.842 | -0.000 | -0.000 | -0.000 |
| 105.291 | 123.296 | 101.892 | -0.000 | -0.000 | -0.000 |
| 75.244 | 100.543 | 109.788 | -0.000 | -0.000 | -0.000 |
| -0.062 | 0.107 | -0.044 | 5.435 | -0.000 | -0.000 |
| -0.204 | 0.407 | -0.153 | -0.000 | 28.372 | -0.000 |
| -0.735 | 1.468 | -0.551 | -0.000 | -0.000 | -8.705 |
| 115.743 | 102.642 | 73.963 | 0.000 | -0.000 | 0.000 |
| 94.370 | 130.412 | 96.254 | 0.000 | -0.000 | 0.000 |
| 86.554 | 81.212 | 117.706 | 0.000 | 0.000 | 0.000 |
| 0.062 | -0.107 | 0.044 | 5.435 | 0.000 | 0.000 |
| 0.204 | -0.407 | 0.153 | 0.000 | 28.372 | 0.000 |
| 0.735 | -1.468 | 0.551 | 0.000 | 0.000 | -8.705 |
| 104.955 | 107.604 | 68.753 | -0.000 | 0.000 | -0.000 |
| 105.434 | 123.024 | 101.997 | 0.000 | -0.000 | -0.000 |
| 68.690 | 104.104 | 106.528 | 0.000 | 0.000 | -0.000 |
| -0.006 | 0.011 | -0.004 | 5.435 | -0.000 | -0.000 |
| -0.020 | 0.041 | -0.015 | -0.000 | 28.370 | -0.000 |
| -0.074 | 0.147 | -0.055 | 0.000 | -0.000 | -8.750 |
| 104.987 | 107.543 | 68.776 | 0.000 | 0.000 | 0.000 |
| 105.464 | 122.966 | 102.019 | -0.000 | -0.000 | 0.000 |
| 86.554 | 81.212 | 117.705 | 0.000 | -0.000 | 0.000 |
| 0.006 | -0.011 | 0.004 | 5.435 | 0.000 | 0.000 |
| 0.020 | -0.041 | 0.015 | -0.000 | 28.370 | 0.000 |
| 0.074 | -0.147 | 0.055 | -0.000 | 0.000 | -8.750 |
| 94.431 | 55.925 | 55.925 | -0.000 | 0.000 | -0.000 |
| 55.925 | 94.431 | 55.925 | -0.000 | 0.000 | -0.000 |
| 55.925 | 55.925 | 94.431 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 16.544 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 16.544 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 16.544 |
| 94.431 | 55.925 | 55.925 | -0.000 | 0.000 | 0.000 |
| 55.925 | 94.431 | 55.925 | 0.000 | -0.000 | 0.000 |
| 55.925 | 55.925 | 94.431 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 16.544 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 16.544 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 16.544 |
| 94.431 | 55.925 | 55.925 | 0.000 | -0.000 | -0.000 |
| 55.925 | 94.431 | 55.925 | 0.000 | 0.000 | -0.000 |
| 55.925 | 55.925 | 94.431 | -0.000 | 0.000 | -0.000 |
| -5.213 | -5.213 | -5.213 | 10.700 | 0.000 | -0.000 |
| -5.213 | -5.213 | -5.213 | 0.000 | 10.700 | -0.000 |
| -5.213 | -5.213 | -5.213 | -0.000 | 0.000 | 10.700 |
| 94.431 | 55.925 | 55.925 | -0.000 | -0.000 | 0.000 |
| 55.925 | 94.431 | 55.925 | -0.000 | -0.000 | 0.000 |
| 55.925 | 55.925 | 94.431 | 0.000 | -0.000 | 0.000 |
| 5.213 | 5.213 | 5.213 | 10.700 | 0.000 | 0.000 |
| 5.213 | 5.213 | 5.213 | 0.000 | 10.700 | 0.000 |
| 5.213 | 5.213 | 5.213 | 0.000 | -0.000 | 10.700 |
| 86.025 | 56.806 | 56.806 | -0.000 | 0.000 | -0.000 |
| 56.806 | 86.025 | 56.806 | -0.000 | 0.000 | -0.000 |
| 56.806 | 56.806 | 86.025 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 16.544 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 16.544 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 16.544 |
| 94.430 | 55.925 | 55.925 | 0.000 | -0.000 | 0.000 |
| 55.925 | 94.430 | 55.925 | -0.000 | -0.000 | 0.000 |
| 55.925 | 55.925 | 94.430 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 16.544 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 16.544 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 16.544 |
| 91.692 | 55.758 | 55.758 | 0.000 | -0.000 | -0.000 |
| 55.758 | 91.692 | 55.758 | -0.000 | 0.000 | -0.000 |
| 55.758 | 55.758 | 91.692 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 16.107 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 16.107 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 16.107 |
| -655.917 | -675.375 | -675.375 | -0.000 | 0.000 | 0.000 |
| -675.375 | -655.917 | -675.375 | 0.000 | -0.000 | 0.000 |
| -675.375 | -675.375 | -655.917 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 16.107 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 16.107 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 16.107 |
| 91.692 | 55.758 | 55.758 | -0.000 | 0.000 | -0.000 |
| 55.758 | 91.692 | 55.758 | -0.000 | -0.000 | -0.000 |
| 55.758 | 55.758 | 91.692 | 0.000 | 0.000 | -0.000 |
| 73.246 | 73.246 | 73.246 | 8.331 | 0.000 | -0.000 |
| 73.246 | 73.246 | 73.246 | 0.000 | 8.331 | -0.000 |
| 73.246 | 73.246 | 73.246 | -0.000 | -0.000 | 8.331 |
| 7.393 | -20.927 | -20.927 | 0.000 | 0.000 | 0.000 |
| -20.927 | 7.393 | -20.927 | -0.000 | -0.000 | 0.000 |
| -20.927 | -20.927 | 7.393 | -0.000 | 0.000 | 0.000 |
| -73.246 | -73.246 | -73.246 | 8.331 | 0.000 | -0.000 |
| -73.246 | -73.246 | -73.246 | -0.000 | 8.331 | -0.000 |
| -73.246 | -73.246 | -73.246 | -0.000 | -0.000 | 8.331 |
| 85.446 | 63.824 | 63.824 | 0.000 | 0.000 | -0.000 |
| 63.824 | 85.446 | 63.824 | 0.000 | 0.000 | 0.000 |
| 63.824 | 63.824 | 85.446 | 0.000 | 0.000 | -0.000 |
| 7.549 | 7.549 | 7.549 | 11.355 | -0.000 | -0.000 |
| 7.549 | 7.549 | 7.549 | 0.000 | 11.355 | -0.000 |
| 7.549 | 7.549 | 7.549 | 0.000 | -0.000 | 11.355 |
| 91.691 | 55.757 | 55.757 | -0.000 | -0.000 | 0.000 |
| 55.757 | 91.691 | 55.757 | 0.000 | -0.000 | 0.000 |
| 55.757 | 55.757 | 91.691 | -0.000 | -0.000 | 0.000 |
| -7.549 | -7.549 | -7.549 | 11.355 | -0.000 | 0.000 |
| -7.549 | -7.549 | -7.549 | -0.000 | 11.355 | 0.000 |
| -7.549 | -7.549 | -7.549 | -0.000 | -0.000 | 11.355 |
| 95.885 | 55.805 | 55.805 | 0.000 | -0.000 | 0.000 |
| 55.805 | 95.885 | 55.805 | -0.000 | 0.000 | 0.000 |
| 55.805 | 55.805 | 95.885 | 0.000 | -0.000 | -0.000 |
| 756.608 | 756.608 | 756.608 | -8.400 | -0.000 | -0.000 |
| 756.608 | 756.608 | 756.608 | -0.000 | -8.400 | -0.000 |
| 756.608 | 756.608 | 756.608 | -0.000 | -0.000 | -8.400 |
| 33.097 | 4.518 | 4.518 | 0.000 | 0.000 | 0.000 |
| 4.518 | 33.097 | 4.518 | 0.000 | 0.000 | 0.000 |
| 4.518 | 4.518 | 33.097 | 0.000 | 0.000 | 0.000 |
| -756.608 | -756.608 | -756.608 | -8.400 | 0.000 | 0.000 |
| -756.608 | -756.608 | -756.608 | 0.000 | -8.400 | 0.000 |
| -756.608 | -756.608 | -756.608 | 0.000 | 0.000 | -8.400 |
| 95.885 | 55.805 | 55.805 | 0.000 | 0.000 | -0.000 |
| 55.805 | 95.885 | 55.805 | 0.000 | -0.000 | 0.000 |
| 64.528 | 64.528 | 93.498 | -0.000 | -0.000 | -0.000 |
| 5.469 | 5.469 | 5.469 | 13.114 | -0.000 | -0.000 |
| 5.469 | 5.469 | 5.469 | -0.000 | 13.114 | -0.000 |
| 5.469 | 5.469 | 5.469 | -0.000 | -0.000 | 13.114 |
| -0.020 | -14.880 | -14.880 | 0.000 | 0.000 | 0.000 |
| -14.880 | -0.020 | -14.880 | 0.000 | 0.000 | 0.000 |
| -14.880 | -14.880 | -0.020 | 0.000 | 0.000 | 0.000 |
| -5.469 | -5.469 | -5.469 | 13.114 | 0.000 | 0.000 |
| -5.469 | -5.469 | -5.469 | 0.000 | 13.114 | 0.000 |
| -5.469 | -5.469 | -5.469 | 0.000 | 0.000 | 13.114 |
| 88.332 | 65.976 | 65.976 | -0.000 | -0.000 | -0.000 |
| 65.976 | 88.332 | 65.976 | -0.000 | -0.000 | -0.000 |
| 65.976 | 65.976 | 88.332 | -0.000 | -0.000 | -0.000 |
| 8.805 | 8.805 | 8.805 | -4.313 | -0.000 | -0.000 |
| 8.805 | 8.805 | 8.805 | -0.000 | -4.313 | -0.000 |
| 8.805 | 8.805 | 8.805 | -0.000 | -0.000 | -4.313 |
| 73.742 | 54.322 | 54.322 | 0.000 | 0.000 | 0.000 |
| 54.322 | 73.742 | 54.322 | 0.000 | 0.000 | 0.000 |
| 54.322 | 54.322 | 73.742 | 0.000 | 0.000 | 0.000 |
| -8.805 | -8.805 | -8.805 | -4.313 | 0.000 | 0.000 |
| -8.805 | -8.805 | -8.805 | 0.000 | -4.313 | 0.000 |
| -8.805 | -8.805 | -8.805 | 0.000 | 0.000 | -4.313 |
| 130.045 | 165.037 | 74.567 | 0.000 | -0.000 | -0.000 |
| 114.331 | 180.750 | 74.567 | 0.000 | -0.000 | 0.000 |
| 74.567 | 74.567 | 151.237 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 2.382 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 2.382 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 33.209 |
| 126.200 | 168.881 | 74.567 | -0.000 | 0.000 | 0.000 |
| 168.881 | 126.200 | 74.567 | -0.000 | 0.000 | 0.000 |
| 74.567 | 74.567 | 151.237 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 2.382 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 2.382 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 33.209 |
| 125.286 | 169.795 | 74.567 | 0.000 | -0.000 | 0.000 |
| 168.881 | 126.200 | 74.567 | 0.000 | -0.000 | -0.000 |
| 74.567 | 74.567 | 151.237 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 2.382 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 2.382 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 33.209 |
| 130.044 | 165.037 | 74.567 | -0.000 | 0.000 | -0.000 |
| 165.036 | 130.045 | 74.567 | -0.000 | 0.000 | 0.000 |
| 74.567 | 74.567 | 151.237 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 2.382 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 2.382 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 33.209 |
| 130.046 | 165.036 | 74.567 | 0.000 | -0.000 | -0.000 |
| -6877066.762 | -6946253.349 | -6141445.066 | 9128.871 | -7218.445 | 40237.798 |
| 74.567 | 74.567 | 151.238 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 2.382 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 2.382 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -21.340 |
| 130.043 | 165.037 | 74.567 | -0.000 | 0.000 | 0.000 |
| 6999857.933 | 6997686.115 | 6527339.562 | 22461.314 | -11083.322 | -29060.721 |
| 74.567 | 74.567 | 151.236 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 2.382 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 2.382 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -21.340 |
| 142.108 | 99.548 | 99.548 | 0.000 | 0.000 | -0.000 |
| 99.548 | 142.108 | 99.548 | 0.000 | -0.000 | 0.000 |
| 99.548 | 99.548 | 142.108 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 16.881 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 16.881 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 16.881 |
| 142.108 | 99.548 | 99.548 | -0.000 | -0.000 | -0.000 |
| 99.548 | 142.108 | 99.548 | -0.000 | -0.000 | 0.000 |
| 99.548 | 99.548 | 142.108 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 16.881 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 16.881 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 16.881 |
| 142.108 | 99.548 | 99.548 | 0.000 | 0.000 | 0.000 |
| 99.548 | 142.108 | 99.548 | 0.000 | 0.000 | 0.000 |
| 99.548 | 99.548 | 142.108 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 16.881 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 16.881 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 16.881 |
| 142.108 | 99.548 | 99.548 | -0.000 | -0.000 | 0.000 |
| 99.548 | 142.108 | 99.548 | -0.000 | -0.000 | -0.000 |
| 99.548 | 99.548 | 142.108 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 16.881 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 16.881 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 16.881 |
| 142.107 | 99.548 | 99.548 | 0.000 | -0.000 | 0.000 |
| 99.548 | 142.107 | 99.548 | 0.000 | -0.000 | 0.000 |
| 99.548 | 99.548 | 142.107 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 19.569 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.569 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 19.569 |
| 142.109 | 99.548 | 99.548 | -0.000 | -0.000 | -0.000 |
| 99.548 | 142.109 | 99.548 | -0.000 | -0.000 | -0.000 |
| 99.548 | 99.548 | 142.109 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 19.569 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 19.569 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 19.569 |
| 238.418 | 162.570 | 162.570 | 0.000 | -0.000 | -0.000 |
| 162.570 | 238.418 | 162.570 | 0.000 | -0.000 | -0.000 |
| 162.570 | 162.570 | 238.418 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 45.835 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 45.835 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 45.835 |
| 238.418 | 162.570 | 162.570 | -0.000 | -0.000 | 0.000 |
| 162.570 | 238.418 | 162.570 | -0.000 | 0.000 | 0.000 |
| 162.570 | 162.570 | 238.418 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 45.835 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 45.835 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 45.835 |
| 238.418 | 162.570 | 162.570 | 0.000 | 0.000 | -0.000 |
| 162.570 | 238.418 | 162.570 | 0.000 | 0.000 | 0.000 |
| 162.570 | 162.570 | 238.418 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 45.835 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 45.835 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 45.835 |
| 238.418 | 162.570 | 162.570 | -0.000 | -0.000 | 0.000 |
| 162.570 | 238.418 | 162.570 | -0.000 | 0.000 | 0.000 |
| 162.570 | 162.570 | 238.418 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 45.835 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 45.835 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 45.835 |
| 238.420 | 162.572 | 162.572 | 0.000 | 0.000 | 0.000 |
| 162.572 | 238.420 | 162.572 | 0.000 | -0.000 | 0.000 |
| 162.572 | 162.572 | 238.420 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 90.183 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 90.183 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 90.183 |
| 238.417 | 162.569 | 162.569 | -0.000 | 0.000 | 0.000 |
| 162.569 | 238.417 | 162.569 | -0.000 | 0.000 | 0.000 |
| 162.569 | 162.569 | 238.417 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 90.183 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 90.183 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 90.183 |
| 249.651 | 175.413 | 175.413 | 0.000 | 0.000 | -0.000 |
| 175.413 | 249.651 | 175.413 | 0.000 | 0.000 | -0.000 |
| 175.413 | 175.413 | 249.651 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 26.848 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 26.848 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 26.848 |
| 249.651 | 175.413 | 175.413 | -0.000 | -0.000 | -0.000 |
| 175.413 | 249.651 | 175.413 | 0.000 | -0.000 | -0.000 |
| 175.413 | 175.413 | 249.651 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 26.848 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 26.848 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 26.848 |
| 249.651 | 175.413 | 175.413 | 0.000 | 0.000 | 0.000 |
| 175.413 | 249.651 | 175.413 | 0.000 | 0.000 | -0.000 |
| 175.413 | 175.413 | 249.651 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 87.747 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 87.747 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 87.747 |
| 249.651 | 175.413 | 175.413 | -0.000 | -0.000 | -0.000 |
| 175.413 | 249.651 | 175.413 | -0.000 | -0.000 | -0.000 |
| 175.413 | 175.413 | 249.651 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 87.747 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 87.747 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 87.747 |
| 249.652 | 175.414 | 175.414 | 0.000 | 0.000 | 0.000 |
| 175.414 | 249.652 | 175.414 | 0.000 | 0.000 | 0.000 |
| 175.414 | 175.414 | 249.652 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 26.848 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 26.848 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 26.848 |
| 249.650 | 175.412 | 175.412 | -0.000 | -0.000 | -0.000 |
| 175.412 | 249.650 | 175.412 | -0.000 | -0.000 | -0.000 |
| 175.412 | 175.412 | 249.650 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 26.848 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 26.848 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 26.848 |
| 10.056 | 115.829 | 10.362 | -0.000 | -0.000 | -0.000 |
| 115.829 | 10.056 | 10.362 | -0.000 | -0.000 | 0.000 |
| 45.597 | 45.597 | 131.747 | -0.000 | -0.000 | -0.000 |
| -0.069 | -0.069 | -0.324 | -61.892 | -0.000 | -0.000 |
| -0.069 | -0.069 | -0.324 | -0.000 | -61.892 | -0.000 |
| -0.007 | -0.007 | -0.035 | -0.000 | -0.000 | 53.945 |
| 57.090 | 79.932 | 36.449 | 0.000 | 0.000 | 0.000 |
| 79.932 | 57.090 | 36.449 | 0.000 | 0.000 | -0.000 |
| 45.616 | 45.616 | 131.836 | 0.000 | 0.000 | 0.000 |
| 0.069 | 0.069 | 0.324 | -61.892 | 0.000 | -0.000 |
| 0.069 | 0.069 | 0.324 | 0.000 | -61.892 | 0.000 |
| 0.007 | 0.007 | 0.035 | 0.000 | 0.000 | 53.945 |
| -60788433.007 | -67789217.998 | -40232417.874 | 0.000 | -0.000 | 0.000 |
| -113701073.133 | -113701028.968 | -51489167.359 | 0.000 | 0.001 | -0.000 |
| 50.685 | 50.685 | 155.584 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 17.729 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 17.729 | -0.000 |
| -0.001 | -0.001 | -0.003 | -0.000 | -0.000 | 53.945 |
| 62.622 | 79.698 | 48.859 | 0.000 | 0.000 | -0.000 |
| 79.698 | 62.622 | 48.859 | 0.000 | 0.000 | 0.000 |
| 45.607 | 45.607 | 131.796 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 17.729 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 17.729 | 0.000 |
| 0.001 | 0.001 | 0.003 | 0.000 | 0.000 | 53.945 |
| -6078765.340 | -6778873.526 | -4023212.961 | 0.000 | 0.000 | -0.000 |
| -6778873.526 | -6078765.340 | -4023212.961 | 0.000 | -0.000 | 0.000 |
| 45.607 | 45.607 | 131.793 | -0.000 | -0.000 | -0.000 |
| -0.001 | -0.001 | -0.003 | -61.895 | -0.000 | -0.000 |
| -0.001 | -0.001 | -0.003 | -0.000 | -61.895 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 53.945 |
| 62.621 | 79.698 | 48.859 | 0.000 | 0.000 | -0.000 |
| 79.698 | 62.621 | 48.859 | 0.000 | 0.000 | 0.000 |
| 45.606 | 45.606 | 131.790 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.001 | 0.003 | -61.895 | 0.000 | 0.000 |
| 0.001 | 0.001 | 0.003 | 0.000 | -61.895 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 53.945 |
| 19.858 | 20.883 | 20.883 | 0.000 | 0.000 | 0.000 |
| 20.883 | 19.858 | 20.883 | 0.000 | 0.000 | 0.000 |
| 20.883 | 20.883 | 19.858 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -2.841 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.841 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -2.841 |
| 19.858 | 20.883 | 20.883 | -0.000 | -0.000 | -0.000 |
| 20.883 | 19.858 | 20.883 | -0.000 | -0.000 | -0.000 |
| 20.883 | 20.883 | 19.858 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -2.841 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.841 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -2.841 |
| 19.858 | 20.884 | 20.884 | 0.000 | 0.000 | 0.000 |
| 20.884 | 19.858 | 20.884 | 0.000 | 0.000 | 0.000 |
| 20.884 | 20.884 | 19.858 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -2.841 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.841 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -2.841 |
| 19.858 | 20.883 | 20.883 | -0.000 | -0.000 | -0.000 |
| 20.883 | 19.858 | 20.883 | -0.000 | -0.000 | -0.000 |
| 20.883 | 20.883 | 19.858 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -2.841 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.841 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -2.841 |
| 19.858 | 20.884 | 20.884 | -0.000 | 0.000 | 0.000 |
| 20.884 | 19.858 | 20.884 | 0.000 | -0.000 | 0.000 |
| 20.884 | 20.884 | 19.858 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -2.841 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.841 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -2.841 |
| 19.858 | 20.883 | 20.883 | -0.000 | -0.000 | -0.000 |
| 20.883 | 19.858 | 20.883 | -0.000 | -0.000 | -0.000 |
| 20.883 | 20.883 | 19.858 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -2.841 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.841 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -2.841 |
| 212.083 | 165.827 | 150.098 | 0.000 | 0.000 | 0.000 |
| 165.827 | 212.083 | 150.098 | -0.000 | 0.000 | 0.000 |
| 168.685 | 168.685 | 322.239 | -0.000 | 0.000 | 0.000 |
| 21.200 | 21.200 | 149.887 | 138.521 | 0.000 | 0.000 |
| 21.200 | 21.200 | 149.887 | 0.000 | 138.521 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 155.258 |
| 196.668 | 150.412 | 0.024 | -0.000 | -0.000 | -0.000 |
| 150.412 | 196.668 | 0.024 | -0.000 | -0.000 | -0.000 |
| 126.163 | 126.163 | 21.907 | 0.000 | -0.000 | -0.000 |
| -21.200 | -21.200 | -149.887 | 138.521 | -0.000 | -0.000 |
| -21.200 | -21.200 | -149.887 | -0.000 | 138.521 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 155.258 |
| 212.083 | 165.827 | 150.098 | 0.000 | 0.000 | 0.000 |
| 165.827 | 212.083 | 150.098 | -0.000 | 0.000 | 0.000 |
| 149.344 | 149.344 | 186.673 | 0.000 | 0.000 | 0.000 |
| 0.499 | 0.499 | 6.790 | 137.139 | 0.000 | -0.000 |
| 0.499 | 0.499 | 6.790 | 0.000 | 137.139 | 0.000 |
| 1.014 | 1.014 | 13.802 | -0.000 | 0.000 | 155.258 |
| 208.742 | 162.486 | 131.803 | -0.000 | -0.000 | -0.000 |
| 162.486 | 208.742 | 131.803 | -0.000 | -0.000 | -0.000 |
| 146.536 | 146.536 | 164.358 | -0.000 | -0.000 | -0.000 |
| -0.499 | -0.499 | -6.790 | 137.139 | -0.000 | -0.000 |
| -0.499 | -0.499 | -6.790 | -0.000 | 137.139 | -0.000 |
| -1.014 | -1.014 | -13.802 | -0.000 | -0.000 | 155.258 |
| 211.195 | 164.939 | 149.436 | 0.000 | 0.000 | 0.000 |
| 164.939 | 211.195 | 149.436 | 0.000 | 0.000 | 0.000 |
| 150.098 | 150.098 | 188.149 | -0.000 | 0.000 | 0.000 |
| 0.234 | 0.234 | 1.626 | 138.461 | 0.000 | 0.000 |
| 0.234 | 0.234 | 1.626 | 0.000 | 138.461 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 155.258 |
| 211.002 | 164.746 | 148.681 | -0.000 | -0.000 | -0.000 |
| 164.746 | 211.002 | 148.681 | -0.000 | -0.000 | -0.000 |
| 147.217 | 147.217 | 171.623 | -0.000 | -0.000 | -0.000 |
| -0.234 | -0.234 | -1.626 | 138.461 | -0.000 | -0.000 |
| -0.234 | -0.234 | -1.626 | -0.000 | 138.461 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 155.258 |
| 227.226 | 231.087 | 183.610 | -8.517 | 0.000 | -0.000 |
| 211.382 | 252.334 | 152.159 | 15.470 | 0.000 | -0.000 |
| 146.592 | 146.592 | 321.812 | 0.000 | 0.000 | -0.000 |
| -5.902 | 5.902 | -0.000 | 35.924 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 35.924 | -5.902 |
| 0.141 | 0.141 | 0.360 | 0.000 | -15.892 | 18.436 |
| 313.065 | 179.527 | 149.391 | -5.902 | -0.000 | 0.000 |
| 179.527 | 313.065 | 149.391 | 5.902 | -0.000 | 0.000 |
| 146.592 | 146.592 | 321.812 | 0.000 | -0.000 | 0.000 |
| -3.298 | 2.531 | -0.921 | -28.797 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 35.924 | -5.902 |
| -0.141 | -0.141 | -0.360 | 0.000 | -15.892 | 18.436 |
| 313.065 | 179.527 | 149.391 | -5.902 | 0.000 | -0.000 |
| 179.527 | 313.065 | 149.391 | 5.902 | 0.000 | -0.000 |
| 146.592 | 146.592 | 321.812 | -0.000 | 0.000 | -0.000 |
| -5.902 | 5.902 | 0.000 | 35.924 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 35.924 | -5.902 |
| -0.000 | 0.000 | -0.000 | -0.000 | -5.902 | 66.769 |
| 252.458 | 211.091 | 151.769 | -15.427 | -0.000 | 0.000 |
| 179.527 | 313.065 | 149.391 | 5.901 | -0.000 | 0.000 |
| 148.759 | 148.759 | 259.679 | -0.000 | -0.000 | 0.000 |
| -18.367 | 18.332 | -0.045 | -8.041 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 35.924 | -5.902 |
| -0.000 | -0.000 | -0.000 | 0.000 | -5.902 | 66.769 |
| 227.189 | 231.070 | 183.288 | -8.601 | 0.000 | -0.000 |
| 179.527 | 313.066 | 149.391 | 5.902 | 0.000 | -0.000 |
| 148.774 | 148.774 | 259.677 | -0.000 | 0.000 | -0.000 |
| -18.348 | 18.351 | 0.004 | -8.040 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 35.924 | -5.902 |
| 0.001 | 0.001 | 0.004 | -0.000 | -15.892 | 18.433 |
| 227.191 | 231.068 | 183.280 | -8.602 | -0.000 | 0.000 |
| 231.070 | 227.189 | 183.281 | 8.602 | -0.000 | 0.000 |
| 148.771 | 148.771 | 259.679 | 0.000 | -0.000 | 0.000 |
| -5.902 | 5.902 | -0.000 | 35.924 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 35.924 | -5.902 |
| -0.001 | -0.001 | -0.004 | 0.000 | -15.892 | 18.433 |
| 136.016 | 64.410 | 64.410 | 0.000 | -0.000 | 0.000 |
| 64.410 | 136.016 | 64.410 | 0.000 | -0.000 | 0.000 |
| 64.410 | 64.410 | 136.016 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 7.476 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 7.476 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 7.476 |
| 135.811 | 64.513 | 64.513 | -0.000 | 0.000 | -0.000 |
| 64.513 | 135.811 | 64.513 | -0.000 | 0.000 | -0.000 |
| 64.513 | 64.513 | 135.811 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 7.476 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 7.476 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 7.476 |
| 135.811 | 64.513 | 64.513 | 0.000 | 0.000 | 0.000 |
| 64.513 | 135.811 | 64.513 | -0.000 | -0.000 | 0.000 |
| 64.513 | 64.513 | 135.811 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 7.476 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 7.476 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 7.476 |
| 135.811 | 64.513 | 64.513 | -0.000 | 0.000 | -0.000 |
| 64.513 | 135.811 | 64.513 | 0.000 | 0.000 | -0.000 |
| 64.513 | 64.513 | 135.811 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 7.476 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 7.476 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 7.476 |
| 135.810 | 64.513 | 64.513 | 0.000 | -0.000 | 0.000 |
| 64.513 | 135.810 | 64.513 | 0.000 | -0.000 | 0.000 |
| 64.513 | 64.513 | 135.810 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 7.476 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 7.476 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 7.476 |
| 135.812 | 64.513 | 64.513 | 0.000 | 0.000 | -0.000 |
| 64.513 | 135.812 | 64.513 | 0.000 | 0.000 | -0.000 |
| 64.513 | 64.513 | 135.812 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 7.476 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 7.476 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 7.476 |
| 81.568 | 67.093 | 67.093 | -0.000 | 0.000 | -0.000 |
| 67.093 | 81.568 | 67.093 | -0.000 | -0.000 | 0.000 |
| 67.093 | 67.093 | 81.568 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -80.676 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -80.676 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -80.676 |
| 81.568 | 67.093 | 67.093 | 0.000 | 0.000 | 0.000 |
| 67.093 | 81.568 | 67.093 | 0.000 | 0.000 | -0.000 |
| 67.093 | 67.093 | 81.568 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -80.676 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -80.676 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -80.676 |
| 81.568 | 67.093 | 67.093 | -0.000 | 0.000 | 0.000 |
| 67.093 | 81.568 | 67.093 | -0.000 | -0.000 | -0.000 |
| 67.093 | 67.093 | 81.568 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -80.676 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -80.676 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -80.676 |
| 81.568 | 67.093 | 67.093 | 0.000 | 0.000 | 0.000 |
| 67.093 | 81.568 | 67.093 | 0.000 | 0.000 | -0.000 |
| 67.093 | 67.093 | 81.568 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -80.676 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -80.676 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -80.676 |
| 81.568 | 67.093 | 67.093 | -0.000 | -0.000 | 0.000 |
| 67.093 | 81.568 | 67.093 | -0.000 | 0.000 | 0.000 |
| 67.093 | 67.093 | 81.568 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 25.939 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 25.939 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 25.939 |
| 81.567 | 67.093 | 67.093 | 0.000 | 0.000 | -0.000 |
| 67.093 | 81.567 | 67.093 | 0.000 | 0.000 | -0.000 |
| 67.093 | 67.093 | 81.567 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 25.939 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 25.939 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 25.939 |
| 116.420 | 77.065 | 77.065 | 0.000 | 0.000 | 0.000 |
| 77.065 | 116.420 | 77.065 | 0.000 | 0.000 | 0.000 |
| 77.065 | 77.065 | 116.420 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 22.680 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 22.680 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 22.680 |
| 116.420 | 77.065 | 77.065 | -0.000 | -0.000 | -0.000 |
| 77.065 | 116.420 | 77.065 | 0.000 | -0.000 | -0.000 |
| 77.065 | 77.065 | 116.420 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 22.680 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 22.680 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 22.680 |
| 116.420 | 77.065 | 77.065 | 0.000 | 0.000 | 0.000 |
| 77.065 | 116.420 | 77.065 | 0.000 | 0.000 | 0.000 |
| 77.065 | 77.065 | 116.420 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 22.680 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 22.680 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 22.680 |
| 116.420 | 77.065 | 77.065 | -0.000 | -0.000 | -0.000 |
| 77.065 | 116.420 | 77.065 | -0.000 | -0.000 | -0.000 |
| 77.065 | 77.065 | 116.420 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 22.680 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 22.680 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 22.680 |
| 116.419 | 77.065 | 77.065 | -0.000 | 0.000 | 0.000 |
| 77.065 | 116.419 | 77.065 | 0.000 | 0.000 | 0.000 |
| 77.065 | 77.065 | 116.419 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 22.680 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 22.680 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 22.680 |
| 116.420 | 77.066 | 77.066 | -0.000 | -0.000 | -0.000 |
| 77.066 | 116.420 | 77.066 | -0.000 | -0.000 | -0.000 |
| 77.066 | 77.066 | 116.420 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 22.680 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 22.680 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 22.680 |
| 42.950 | 139.006 | 62.350 | 0.000 | -0.000 | 0.000 |
| 139.006 | 42.950 | 62.350 | 0.000 | -0.000 | 0.000 |
| 62.350 | 62.350 | 86.498 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 12.486 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 12.486 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 25.095 |
| 105.075 | 76.880 | 62.350 | -0.000 | 0.000 | -0.000 |
| 76.880 | 105.075 | 62.350 | -0.000 | 0.000 | -0.000 |
| 62.350 | 62.350 | 86.498 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 12.486 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 12.486 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 25.095 |
| 105.075 | 76.880 | 62.350 | 0.000 | -0.000 | 0.000 |
| 76.880 | 105.075 | 62.350 | 0.000 | -0.000 | 0.000 |
| 62.350 | 62.350 | 86.498 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -1.626 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -1.626 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 25.095 |
| 42.950 | 139.006 | 62.350 | -0.000 | 0.000 | -0.000 |
| 139.006 | 42.950 | 62.350 | -0.000 | -0.000 | -0.000 |
| 62.350 | 62.350 | 86.498 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -1.626 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -1.626 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 25.095 |
| 23.823 | 158.131 | 62.348 | 0.000 | -0.000 | 0.000 |
| 158.131 | 23.823 | 62.348 | 0.000 | -0.000 | 0.000 |
| 62.350 | 62.350 | 86.498 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 12.486 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 12.486 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 25.095 |
| 17.941 | 164.017 | 62.351 | -0.000 | -0.000 | -0.000 |
| 164.017 | 17.941 | 62.351 | -0.000 | -0.000 | -0.000 |
| 62.350 | 62.350 | 86.498 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 12.486 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 12.486 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 25.095 |
| 227.419 | 103.519 | 103.519 | 0.000 | -0.000 | -0.000 |
| 103.519 | 227.419 | 103.519 | -0.000 | -0.000 | -0.000 |
| 103.519 | 103.519 | 227.419 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 19.754 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 19.754 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 19.754 |
| 227.419 | 103.519 | 103.519 | 0.000 | -0.000 | 0.000 |
| 103.519 | 227.419 | 103.519 | 0.000 | -0.000 | 0.000 |
| 103.519 | 103.519 | 227.419 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 19.754 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 19.754 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 19.754 |
| 227.419 | 103.519 | 103.519 | 0.000 | -0.000 | 0.000 |
| 103.519 | 227.419 | 103.519 | 0.000 | 0.000 | -0.000 |
| 103.519 | 103.519 | 227.419 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 19.719 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.719 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 19.719 |
| 227.418 | 103.519 | 103.519 | -0.000 | 0.000 | 0.000 |
| 103.519 | 227.418 | 103.519 | 0.000 | -0.000 | 0.000 |
| 103.519 | 103.519 | 227.418 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 19.719 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 19.719 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 19.719 |
| 227.421 | 103.520 | 103.520 | -0.000 | 0.000 | -0.000 |
| 103.520 | 227.421 | 103.520 | -0.000 | 0.000 | -0.000 |
| 103.520 | 103.520 | 227.421 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 19.754 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.754 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 19.754 |
| 227.417 | 103.519 | 103.519 | -0.000 | -0.000 | 0.000 |
| 103.519 | 227.417 | 103.519 | 0.000 | -0.000 | 0.000 |
| 103.519 | 103.519 | 227.417 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 19.754 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 19.754 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 19.754 |
| 171.027 | 149.516 | 149.516 | 0.000 | 0.000 | 0.000 |
| 149.516 | 171.027 | 149.516 | 0.000 | 0.000 | 0.000 |
| 149.516 | 149.516 | 171.027 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 95.021 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 95.021 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 95.021 |
| 171.027 | 149.516 | 149.516 | -0.000 | 0.000 | -0.000 |
| 149.516 | 171.027 | 149.516 | -0.000 | 0.000 | -0.000 |
| 149.516 | 149.516 | 171.027 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 95.021 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 95.021 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 95.021 |
| 171.027 | 149.516 | 149.516 | 0.000 | 0.000 | 0.000 |
| 149.516 | 171.027 | 149.516 | 0.000 | 0.000 | 0.000 |
| 149.516 | 149.516 | 171.027 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 90.354 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 90.354 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 90.354 |
| 171.027 | 149.516 | 149.516 | -0.000 | -0.000 | -0.000 |
| 149.516 | 171.027 | 149.516 | -0.000 | 0.000 | -0.000 |
| 149.516 | 149.516 | 171.027 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 90.354 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 90.354 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 90.354 |
| 171.028 | 149.516 | 149.516 | 0.000 | 0.000 | 0.000 |
| 149.516 | 171.028 | 149.516 | 0.000 | 0.000 | 0.000 |
| 149.516 | 149.516 | 171.028 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 95.021 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 95.021 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 95.021 |
| 171.027 | 149.516 | 149.516 | -0.000 | -0.000 | -0.000 |
| 149.516 | 171.027 | 149.516 | -0.000 | -0.000 | -0.000 |
| 149.516 | 149.516 | 171.027 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 95.021 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 95.021 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 95.021 |
| 198.233 | 125.935 | 125.935 | 0.000 | 0.000 | 0.000 |
| 125.935 | 198.233 | 125.935 | 0.000 | 0.000 | 0.000 |
| 125.935 | 125.935 | 198.233 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 46.992 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 46.992 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 46.992 |
| 198.233 | 125.935 | 125.935 | -0.000 | -0.000 | -0.000 |
| 125.935 | 198.233 | 125.935 | -0.000 | -0.000 | 0.000 |
| 125.935 | 125.935 | 198.233 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 46.992 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 46.992 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 46.992 |
| 198.233 | 125.935 | 125.935 | 0.000 | 0.000 | 0.000 |
| 125.935 | 198.233 | 125.935 | 0.000 | 0.000 | 0.000 |
| 125.935 | 125.935 | 198.233 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 46.992 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 46.992 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 46.992 |
| 198.233 | 125.935 | 125.935 | -0.000 | -0.000 | -0.000 |
| 125.935 | 198.233 | 125.935 | -0.000 | -0.000 | -0.000 |
| 125.935 | 125.935 | 198.233 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 46.992 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 46.992 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 46.992 |
| 198.234 | 125.935 | 125.935 | 0.000 | 0.000 | -0.000 |
| 125.935 | 198.234 | 125.935 | 0.000 | 0.000 | 0.000 |
| 125.935 | 125.935 | 198.234 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 46.992 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 46.992 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 46.992 |
| 198.232 | 125.935 | 125.935 | -0.000 | -0.000 | -0.000 |
| 125.935 | 198.232 | 125.935 | -0.000 | -0.000 | 0.000 |
| 125.935 | 125.935 | 198.232 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 46.992 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 46.992 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 46.992 |
| 333.481 | 77.113 | 129.020 | 0.061 | 0.000 | -0.000 |
| 286.383 | 182.993 | 31.004 | -0.026 | 0.000 | -0.000 |
| 262.707 | 61.873 | 213.177 | 0.146 | 0.000 | 0.000 |
| 154.161 | -33.326 | 54.230 | 43.321 | 0.000 | -0.000 |
| 156.087 | -37.147 | 47.762 | -0.078 | 15.058 | 0.000 |
| 194.241 | -40.533 | 14.011 | 0.088 | 0.000 | 41.136 |
| 183.528 | 111.633 | 92.719 | 0.000 | -0.000 | -0.000 |
| -47.248 | 226.355 | 35.668 | 0.001 | -0.000 | 0.000 |
| -47.739 | 122.969 | 101.266 | -0.006 | -0.000 | 0.000 |
| -196.154 | 40.658 | -13.212 | 41.622 | -0.000 | 0.000 |
| -156.087 | 37.147 | -47.762 | 0.078 | 15.057 | -0.000 |
| -194.241 | 40.533 | -14.011 | -0.088 | -0.000 | 41.136 |
| 161.489 | 113.048 | 100.982 | 0.002 | 0.000 | 0.000 |
| 126.801 | 197.810 | 100.951 | 0.003 | 0.000 | -0.000 |
| 106.259 | 99.816 | 173.158 | 0.002 | 0.000 | -0.000 |
| 17.639 | -3.612 | 0.796 | 42.505 | -0.000 | -0.000 |
| 15.843 | -2.592 | 6.042 | -0.001 | 22.517 | -0.000 |
| 15.534 | -2.731 | 5.958 | 0.003 | 0.000 | 45.578 |
| 183.528 | 111.633 | 92.719 | 0.000 | -0.000 | -0.000 |
| 109.338 | 209.215 | 98.902 | 0.000 | -0.000 | -0.000 |
| 111.958 | 97.535 | 169.350 | -0.005 | -0.000 | 0.000 |
| -17.638 | 3.610 | -0.789 | 42.501 | 0.000 | 0.000 |
| -15.843 | 2.592 | -6.042 | 0.001 | 22.517 | 0.000 |
| -15.534 | 2.731 | -5.958 | -0.003 | -0.000 | 45.578 |
| 148.320 | 112.747 | 112.364 | 0.000 | 0.000 | -0.000 |
| 112.434 | 200.184 | 95.779 | 0.000 | 0.000 | 0.000 |
| 105.989 | 99.126 | 174.087 | 0.000 | 0.000 | 0.000 |
| 0.458 | 0.019 | -0.284 | 44.393 | 0.000 | 0.000 |
| 0.943 | -0.123 | 0.111 | 0.001 | 22.531 | -0.000 |
| 1.562 | -0.250 | 0.617 | -0.000 | 0.000 | 45.591 |
| 153.985 | 112.520 | 106.274 | -0.000 | -0.000 | -0.000 |
| 109.298 | 200.713 | 94.523 | -0.000 | -0.000 | -0.000 |
| 106.392 | 98.943 | 173.835 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 46.815 | -0.000 | 0.000 |
| -1.528 | 0.256 | -0.636 | -0.000 | 22.513 | -0.000 |
| -1.562 | 0.250 | -0.617 | 0.000 | -0.000 | 45.591 |
| 213.513 | 137.323 | 125.847 | 0.000 | 0.000 | -0.000 |
| 157.661 | 264.128 | 126.589 | -0.000 | 0.000 | -0.000 |
| 125.847 | 135.984 | 185.252 | 0.000 | 0.000 | -0.000 |
| 24.709 | 34.476 | 4.472 | 44.795 | 0.000 | -0.000 |
| 27.879 | 38.898 | 5.046 | -0.000 | 39.852 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 52.353 |
| 170.139 | 99.375 | 127.031 | -0.000 | 0.000 | 0.000 |
| 102.821 | 198.691 | 130.819 | 0.000 | -0.000 | 0.000 |
| 108.737 | 95.936 | 150.874 | 0.000 | -0.000 | 0.000 |
| -24.709 | -34.476 | -4.472 | 44.795 | -0.000 | 0.000 |
| -27.879 | -38.898 | -5.046 | 0.000 | 39.852 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 52.353 |
| 203.195 | 130.741 | 121.465 | -0.000 | 0.000 | -0.000 |
| 133.597 | 235.706 | 127.948 | -0.000 | 0.000 | -0.000 |
| 125.847 | 135.984 | 185.252 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 52.096 | 0.000 | 0.000 |
| 2.378 | 3.318 | 0.430 | -0.000 | 40.604 | -0.000 |
| 1.055 | 1.472 | 0.191 | -0.000 | 0.000 | 50.430 |
| 213.513 | 137.323 | 125.847 | -0.000 | -0.000 | 0.000 |
| 132.964 | 234.127 | 124.610 | 0.000 | -0.000 | 0.000 |
| 125.847 | 135.984 | 185.252 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 52.096 | -0.000 | 0.000 |
| -2.378 | -3.318 | -0.430 | 0.000 | 40.604 | 0.000 |
| -1.055 | -1.472 | -0.191 | 0.000 | -0.000 | 50.430 |
| 213.514 | 137.323 | 125.847 | -0.000 | 0.000 | -0.000 |
| 130.723 | 231.869 | 127.850 | -0.000 | 0.000 | -0.000 |
| 123.908 | 124.023 | 167.003 | -0.000 | 0.000 | -0.000 |
| 0.079 | 0.110 | 0.014 | 49.764 | 0.000 | -0.000 |
| 0.283 | 0.376 | 0.001 | -0.000 | 38.696 | -0.000 |
| 0.090 | 0.125 | 0.016 | -0.000 | 0.000 | 50.719 |
| 200.952 | 127.768 | 121.009 | 0.000 | -0.000 | 0.000 |
| 137.323 | 250.213 | 135.983 | 0.000 | -0.000 | 0.000 |
| 124.356 | 128.009 | 160.057 | -0.000 | -0.000 | 0.000 |
| -0.079 | -0.110 | -0.014 | 49.764 | -0.000 | 0.000 |
| -0.283 | -0.376 | -0.001 | 0.000 | 38.696 | 0.000 |
| -0.090 | -0.125 | -0.016 | 0.000 | -0.000 | 50.719 |
| 147.472 | 299.479 | 317.358 | -0.015 | 0.000 | 0.000 |
| 71.880 | 394.951 | 287.639 | 0.035 | 0.000 | 0.000 |
| 70.777 | 287.752 | 357.381 | 0.032 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 46.606 | 0.000 | -0.000 |
| 4.141 | 186.289 | 207.691 | -0.009 | 22.824 | 0.000 |
| 4.666 | 186.268 | 207.589 | -0.009 | 0.000 | 46.277 |
| 183.954 | 111.622 | 93.134 | -0.000 | -0.000 | 0.000 |
| 109.393 | 208.812 | 98.969 | -0.000 | -0.000 | 0.000 |
| 116.144 | -107.363 | -26.077 | -0.013 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 46.606 | -0.000 | 0.000 |
| -4.141 | -186.289 | -207.691 | 0.009 | 22.824 | -0.000 |
| -4.666 | -186.268 | -207.589 | 0.009 | -0.000 | 46.277 |
| 149.245 | 127.670 | 116.470 | -0.004 | 0.000 | 0.000 |
| 115.484 | 217.017 | 102.805 | -0.003 | 0.000 | 0.000 |
| 107.291 | 114.096 | 185.407 | -0.003 | 0.000 | 0.000 |
| -4.044 | 19.193 | 19.467 | 44.125 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 41.095 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 56.306 |
| 154.314 | 96.692 | 102.714 | -0.001 | 0.000 | -0.000 |
| 105.029 | 190.979 | 94.713 | 0.004 | -0.000 | 0.000 |
| 115.760 | 79.403 | 160.556 | -0.002 | 0.000 | -0.000 |
| -0.388 | -18.603 | -20.778 | 43.815 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 41.095 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 56.306 |
| 154.143 | 113.667 | 107.337 | -0.000 | 0.000 | 0.000 |
| 109.688 | 202.082 | 96.638 | 0.000 | 0.000 | 0.000 |
| 107.700 | 97.096 | 166.425 | -0.000 | 0.000 | 0.000 |
| -1.367 | 1.949 | 2.217 | 44.044 | -0.000 | 0.000 |
| 0.034 | 1.843 | 2.067 | -0.000 | 22.618 | 0.000 |
| -0.001 | 1.865 | 2.048 | -0.000 | 0.000 | 45.607 |
| 142.578 | 111.800 | 108.579 | 0.000 | -0.000 | -0.000 |
| 109.392 | 208.811 | 98.968 | 0.000 | -0.000 | -0.000 |
| 108.508 | 93.685 | 162.298 | 0.000 | -0.000 | -0.000 |
| 1.367 | -1.949 | -2.217 | 44.045 | 0.000 | -0.000 |
| -0.034 | -1.843 | -2.067 | 0.000 | 22.618 | -0.000 |
| 0.001 | -1.865 | -2.048 | 0.000 | -0.000 | 45.607 |
| 201.461 | 145.388 | 117.506 | -0.000 | -0.000 | 0.000 |
| 145.388 | 201.461 | 117.506 | -0.000 | 0.000 | 0.000 |
| 117.506 | 117.506 | 171.934 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 33.974 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 33.974 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 58.998 |
| 188.154 | 158.695 | 117.506 | 0.000 | 0.000 | -0.000 |
| 158.695 | 188.154 | 117.506 | 0.000 | -0.000 | -0.000 |
| 117.506 | 117.506 | 171.934 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 33.974 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 33.974 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 58.998 |
| 188.154 | 158.695 | 117.506 | -0.000 | 0.000 | 0.000 |
| 158.695 | 188.154 | 117.506 | -0.000 | 0.000 | 0.000 |
| 117.506 | 117.506 | 171.934 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 33.974 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 33.974 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 58.998 |
| 201.461 | 145.388 | 117.506 | 0.000 | -0.000 | -0.000 |
| 145.388 | 201.461 | 117.506 | 0.000 | 0.000 | -0.000 |
| 117.506 | 117.506 | 171.934 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 33.974 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 33.974 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 58.998 |
| 188.155 | 158.696 | 117.506 | -0.000 | 0.000 | 0.000 |
| 158.696 | 188.155 | 117.506 | 0.000 | 0.000 | 0.000 |
| 117.506 | 117.506 | 171.933 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 31.242 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 31.242 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 58.998 |
| 201.461 | 145.388 | 117.506 | 0.000 | -0.000 | -0.000 |
| 145.388 | 201.461 | 117.506 | 0.000 | -0.000 | -0.000 |
| 117.506 | 117.506 | 171.935 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 31.242 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 31.242 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 58.998 |
| 172.577 | 106.771 | 133.800 | 0.000 | 0.000 | 0.000 |
| 105.622 | 184.767 | 133.799 | -0.000 | 0.000 | -0.000 |
| 134.526 | 134.526 | 281.454 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 65.250 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 65.250 | 0.000 |
| 5.986 | 5.986 | -0.001 | 0.000 | -0.000 | 27.997 |
| 165.614 | 93.301 | 133.802 | -0.000 | -0.000 | 0.000 |
| 102.624 | 158.935 | 133.801 | 0.000 | -0.000 | 0.000 |
| 128.555 | 128.555 | 281.455 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 65.250 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 65.250 | 0.000 |
| -5.986 | -5.986 | 0.001 | -0.000 | 0.000 | 27.997 |
| 184.767 | 105.622 | 133.799 | 0.000 | 0.000 | 0.000 |
| 99.610 | 170.888 | 133.801 | -0.000 | -0.000 | 0.000 |
| 135.124 | 135.124 | 281.454 | 0.000 | 0.000 | -0.000 |
| 0.597 | 0.597 | -0.000 | 64.528 | 0.000 | -0.000 |
| 1.484 | 1.484 | -0.000 | -0.000 | 64.749 | 0.000 |
| -0.135 | -0.135 | 0.000 | 0.000 | 0.000 | 28.049 |
| 184.767 | 105.622 | 133.799 | -0.000 | 0.000 | 0.000 |
| 108.084 | 164.392 | 133.801 | -0.000 | -0.000 | 0.000 |
| 134.526 | 134.526 | 281.454 | 0.000 | -0.000 | -0.000 |
| -0.597 | -0.597 | 0.000 | 64.528 | -0.000 | 0.000 |
| -1.484 | -1.484 | 0.000 | -0.000 | 64.749 | -0.000 |
| 0.135 | 0.135 | -0.000 | 0.000 | -0.000 | 28.049 |
| 170.530 | 99.083 | 133.801 | 0.000 | 0.000 | -0.000 |
| 99.083 | 170.530 | 133.801 | 0.000 | 0.000 | 0.000 |
| 134.526 | 134.526 | 281.455 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 65.250 | -0.000 | -0.000 |
| 0.213 | 0.213 | 0.000 | -0.000 | 64.532 | 0.000 |
| 0.175 | 0.175 | -0.000 | 0.000 | 0.000 | 30.314 |
| 170.445 | 98.967 | 133.801 | -0.000 | -0.000 | 0.000 |
| 105.622 | 184.766 | 133.799 | -0.000 | -0.000 | 0.000 |
| 134.467 | 134.467 | 281.453 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 65.250 | 0.000 | 0.000 |
| -0.213 | -0.213 | -0.000 | 0.000 | 64.532 | -0.000 |
| -0.175 | -0.175 | 0.000 | -0.000 | -0.000 | 30.314 |
| 177.831 | 102.965 | 135.823 | -0.000 | 0.000 | 0.000 |
| 102.965 | 177.831 | 135.823 | -0.000 | 0.000 | 0.000 |
| 135.823 | 135.823 | 285.608 | -0.000 | 0.000 | 0.000 |
| 0.301 | 0.301 | 0.008 | 65.396 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 65.932 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 37.433 |
| 177.831 | 102.965 | 135.823 | 0.000 | -0.000 | -0.000 |
| 102.965 | 177.831 | 135.823 | -0.000 | -0.000 | -0.000 |
| 135.823 | 135.823 | 285.608 | 0.000 | 0.000 | -0.000 |
| -0.301 | -0.301 | -0.008 | 65.396 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 65.932 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 37.433 |
| 162.768 | 96.169 | 135.522 | 0.000 | -0.000 | 0.000 |
| 102.965 | 177.831 | 135.823 | 0.000 | 0.000 | 0.000 |
| 135.585 | 135.585 | 285.602 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 65.932 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 65.932 | 0.000 |
| 0.026 | 0.026 | 0.001 | -0.000 | -0.000 | 27.607 |
| 177.831 | 102.965 | 135.823 | -0.000 | -0.000 | -0.000 |
| 102.965 | 177.831 | 135.823 | -0.000 | -0.000 | -0.000 |
| 135.823 | 135.823 | 285.608 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 65.932 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 65.932 | -0.000 |
| -0.026 | -0.026 | -0.001 | 0.000 | 0.000 | 27.607 |
| 162.763 | 96.161 | 135.522 | -0.000 | 0.000 | 0.000 |
| 106.105 | 157.229 | 135.583 | -0.000 | 0.000 | 0.000 |
| 135.824 | 135.824 | 285.610 | -0.000 | 0.000 | 0.000 |
| 0.003 | 0.003 | 0.000 | 65.389 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 65.932 | 0.000 |
| 0.003 | 0.003 | 0.000 | -0.000 | -0.000 | 27.607 |
| 177.831 | 102.965 | 135.823 | -0.000 | -0.000 | -0.000 |
| 102.965 | 177.831 | 135.823 | 0.000 | -0.000 | -0.000 |
| 135.823 | 135.823 | 285.607 | -0.000 | 0.000 | -0.000 |
| -0.003 | -0.003 | -0.000 | 65.389 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 65.932 | -0.000 |
| -0.003 | -0.003 | -0.000 | 0.000 | 0.000 | 27.607 |
| 314.016 | 154.620 | 137.848 | -30.771 | 0.000 | -0.000 |
| 154.620 | 314.016 | 137.848 | 30.771 | -0.000 | -0.000 |
| 139.130 | 139.130 | 336.927 | -0.000 | 0.000 | -0.000 |
| -13.364 | 12.010 | 0.279 | 51.577 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 60.950 | -30.771 |
| 0.000 | 0.000 | 0.000 | 0.000 | -30.771 | 79.698 |
| 282.345 | 167.021 | 141.703 | -20.641 | -0.000 | -0.000 |
| 191.010 | 268.418 | 139.678 | 11.374 | -0.000 | 0.000 |
| 137.360 | 137.360 | 337.634 | 0.000 | 0.000 | 0.000 |
| -30.771 | 30.771 | -0.000 | 60.950 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 60.950 | -30.771 |
| -0.000 | -0.000 | -0.000 | -0.000 | -30.771 | 79.698 |
| 282.807 | 166.275 | 141.765 | -20.919 | 0.000 | -0.000 |
| 154.620 | 314.016 | 137.849 | 30.771 | 0.000 | -0.000 |
| 139.288 | 139.288 | 336.862 | 0.000 | 0.000 | -0.000 |
| -12.614 | 12.478 | 0.028 | 51.504 | -0.000 | -0.000 |
| 0.003 | 0.003 | -0.000 | 0.000 | 51.179 | -11.170 |
| -0.068 | -0.068 | 0.028 | 0.000 | -12.552 | 40.065 |
| 314.016 | 154.620 | 137.848 | -30.771 | 0.000 | 0.000 |
| 154.620 | 314.016 | 137.848 | 30.771 | 0.000 | 0.000 |
| 137.360 | 137.360 | 337.634 | 0.000 | 0.000 | 0.000 |
| -11.173 | 11.167 | 0.000 | 51.179 | -0.000 | 0.000 |
| -0.003 | -0.003 | 0.000 | -0.000 | 51.179 | -11.170 |
| 0.068 | 0.068 | -0.028 | -0.000 | -12.552 | 40.065 |
| 268.238 | 190.838 | 139.757 | -11.372 | 0.000 | -0.000 |
| 190.838 | 268.240 | 139.757 | 11.372 | 0.000 | -0.000 |
| 139.305 | 139.305 | 336.856 | -0.000 | 0.000 | -0.000 |
| -30.771 | 30.771 | 0.000 | 60.950 | -0.000 | -0.000 |
| -0.007 | -0.007 | 0.003 | 0.000 | 51.503 | -12.544 |
| -0.007 | -0.007 | 0.003 | 0.000 | -12.552 | 40.064 |
| 314.015 | 154.619 | 137.848 | -30.771 | 0.000 | 0.000 |
| 166.347 | 282.762 | 141.758 | 20.892 | -0.000 | 0.000 |
| 139.308 | 139.308 | 336.852 | 0.000 | 0.000 | 0.000 |
| -30.771 | 30.771 | -0.000 | 60.950 | -0.000 | 0.000 |
| 0.007 | 0.007 | -0.003 | -0.000 | 51.503 | -12.544 |
| 0.007 | 0.007 | -0.003 | -0.000 | -12.552 | 40.064 |
| 316.558 | 155.544 | 138.207 | -31.350 | 0.000 | 0.000 |
| 155.544 | 316.558 | 138.207 | 31.350 | 0.000 | -0.000 |
| 1728.817 | 1728.817 | -346.995 | 0.000 | 0.000 | 0.000 |
| 1563.175 | 1614.310 | -681.657 | 59.076 | 0.000 | 0.000 |
| 1588.742 | 1588.742 | -681.657 | 0.000 | 59.076 | -25.568 |
| -0.000 | -0.000 | 0.000 | -0.000 | -31.350 | 80.507 |
| -1172.239 | -1255.789 | 748.621 | -12.994 | -0.000 | -0.000 |
| -1255.789 | -1172.239 | 748.621 | 12.994 | -0.000 | -0.000 |
| -1448.656 | -1448.656 | 1016.315 | -0.000 | -0.000 | -0.000 |
| -1614.310 | -1563.175 | 681.657 | 59.076 | -0.000 | -0.000 |
| -1588.742 | -1588.742 | 681.657 | -0.000 | 59.076 | -25.568 |
| 0.000 | 0.000 | -0.000 | 0.000 | -31.350 | 80.507 |
| 316.558 | 155.544 | 138.207 | -31.350 | 0.000 | 0.000 |
| 322.988 | 458.647 | 71.822 | 25.512 | -0.000 | 0.000 |
| 284.841 | 284.841 | 273.727 | 0.000 | 0.000 | 0.000 |
| 133.370 | 184.501 | -68.192 | 59.075 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 62.079 | -31.350 |
| 159.132 | 159.132 | -68.276 | -0.000 | -25.558 | 67.930 |
| 125.762 | 47.468 | 201.161 | -11.538 | -0.000 | -0.000 |
| 155.544 | 316.558 | 138.207 | 31.350 | -0.000 | -0.000 |
| -18.796 | -18.796 | 402.827 | -0.000 | -0.000 | -0.000 |
| -31.350 | 31.350 | -0.000 | 62.079 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 62.079 | -31.350 |
| -159.132 | -159.132 | 68.276 | 0.000 | -25.558 | 67.930 |
| 316.559 | 155.544 | 138.208 | -31.350 | 0.000 | 0.000 |
| 205.790 | 285.416 | 134.244 | 11.828 | 0.000 | 0.000 |
| 155.997 | 155.997 | 327.833 | 0.000 | 0.000 | 0.000 |
| -8.852 | 41.841 | -7.077 | 58.961 | 0.000 | 0.000 |
| 16.495 | 16.495 | -7.077 | 0.000 | 58.961 | -25.347 |
| 18.291 | 18.291 | -7.848 | -0.000 | -24.693 | 66.051 |
| 281.203 | 146.284 | 147.796 | -25.342 | -0.000 | -0.000 |
| 146.284 | 281.203 | 147.796 | 25.342 | -0.000 | -0.000 |
| 125.880 | 125.880 | 340.635 | -0.000 | -0.000 | -0.000 |
| -26.490 | -2.429 | 6.085 | 52.453 | -0.000 | -0.000 |
| -16.495 | -16.495 | 7.077 | -0.000 | 58.961 | -25.347 |
| -18.291 | -18.291 | 7.848 | 0.000 | -24.693 | 66.051 |
| 283.254 | 165.986 | 141.884 | 21.097 | -0.000 | -0.000 |
| 165.986 | 283.254 | 141.884 | -21.097 | 0.000 | -0.000 |
| 139.271 | 139.271 | 336.928 | -0.000 | 0.000 | -0.000 |
| 12.146 | -13.159 | 0.212 | 51.621 | 0.000 | 0.000 |
| -0.507 | -0.507 | 0.212 | 0.000 | 51.621 | 12.652 |
| -0.508 | -0.508 | 0.213 | 0.000 | 12.602 | 40.156 |
| 314.256 | 154.698 | 137.902 | 30.817 | -0.000 | 0.000 |
| 191.079 | 268.575 | 139.764 | -11.400 | -0.000 | 0.000 |
| 137.438 | 137.438 | 337.666 | -0.000 | -0.000 | 0.000 |
| 13.159 | -12.146 | -0.212 | 51.621 | -0.000 | 0.000 |
| 0.507 | 0.507 | -0.212 | -0.000 | 51.621 | 12.652 |
| 0.508 | 0.508 | -0.213 | 0.000 | 12.602 | 40.156 |
| 314.256 | 154.698 | 137.902 | 30.817 | 0.000 | 0.000 |
| 166.423 | 282.985 | 141.846 | -20.935 | 0.000 | -0.000 |
| 137.438 | 137.438 | 337.666 | 0.000 | 0.000 | -0.000 |
| 30.817 | -30.817 | 0.000 | 61.038 | 0.000 | -0.000 |
| -0.051 | -0.051 | 0.021 | -0.000 | 51.579 | 12.571 |
| 0.000 | 0.000 | 0.000 | 0.000 | 30.817 | 79.779 |
| 282.923 | 166.522 | 141.838 | 20.897 | -0.000 | 0.000 |
| 154.698 | 314.256 | 137.902 | -30.817 | -0.000 | 0.000 |
| 137.438 | 137.438 | 337.666 | -0.000 | -0.000 | 0.000 |
| 30.817 | -30.817 | -0.000 | 61.038 | -0.000 | 0.000 |
| 0.051 | 0.051 | -0.021 | 0.000 | 51.579 | 12.571 |
| -0.000 | -0.000 | -0.000 | -0.000 | 30.817 | 79.779 |
| 314.257 | 154.698 | 137.902 | 30.818 | 0.000 | -0.000 |
| 154.698 | 314.257 | 137.902 | -30.818 | 0.000 | -0.000 |
| 139.397 | 139.397 | 336.876 | 0.000 | 0.000 | -0.000 |
| 11.195 | -11.195 | -0.000 | 51.255 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 51.255 | 11.195 |
| 0.000 | 0.000 | 0.000 | -0.000 | 11.195 | 38.738 |
| 282.950 | 166.477 | 141.841 | 20.914 | -0.000 | 0.000 |
| 154.698 | 314.255 | 137.901 | -30.817 | -0.000 | -0.000 |
| 137.438 | 137.438 | 337.664 | 0.000 | -0.000 | 0.000 |
| 11.194 | -11.195 | 0.000 | 51.254 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 51.255 | 11.195 |
| -0.000 | -0.000 | -0.000 | 0.000 | 11.195 | 38.738 |
| 235.587 | 150.973 | 126.936 | -0.000 | -0.000 | -0.000 |
| 147.737 | 237.733 | 93.302 | 0.000 | -0.000 | -0.000 |
| 134.923 | 99.349 | 225.292 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 78.359 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 113.217 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 130.405 |
| 235.587 | 150.973 | 126.936 | 0.000 | -0.000 | 0.000 |
| 151.665 | 241.678 | 92.829 | 0.000 | 0.000 | 0.000 |
| 133.794 | 98.233 | 225.610 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 78.359 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 113.217 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 130.405 |
| 235.588 | 150.973 | 126.936 | -0.000 | 0.000 | -0.000 |
| 147.621 | 237.618 | 93.339 | -0.000 | 0.000 | -0.000 |
| 131.086 | 96.288 | 233.786 | -0.000 | 0.000 | -0.000 |
| 0.022 | 0.021 | -0.007 | 77.362 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 113.217 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 130.405 |
| 231.428 | 146.815 | 127.626 | 0.000 | -0.000 | 0.000 |
| 151.665 | 241.678 | 92.829 | -0.000 | 0.000 | 0.000 |
| 134.325 | 98.753 | 225.412 | 0.000 | -0.000 | 0.000 |
| -0.022 | -0.021 | 0.007 | 77.362 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 113.217 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 130.405 |
| 235.588 | 150.973 | 126.936 | -0.000 | 0.000 | -0.000 |
| 147.609 | 237.607 | 93.343 | -0.000 | 0.000 | -0.000 |
| 131.087 | 96.288 | 233.787 | -0.000 | -0.000 | -0.000 |
| 0.002 | 0.002 | -0.000 | 77.362 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.001 | -0.000 | 113.217 | -0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | 0.000 | 130.405 |
| 231.440 | 146.827 | 127.621 | 0.000 | -0.000 | 0.000 |
| 151.665 | 241.677 | 92.829 | 0.000 | -0.000 | 0.000 |
| 134.376 | 98.803 | 225.397 | 0.000 | 0.000 | 0.000 |
| -0.002 | -0.002 | 0.000 | 77.362 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.001 | -0.000 | 113.217 | 0.000 |
| -0.000 | -0.001 | -0.000 | 0.000 | -0.000 | 130.405 |
| 244.819 | 133.690 | 134.591 | -0.000 | 0.000 | 0.000 |
| 136.868 | 242.481 | 111.447 | -0.000 | 0.000 | 0.000 |
| 133.120 | 111.939 | 242.316 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 92.444 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 117.883 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 116.246 |
| 244.819 | 133.690 | 134.591 | 0.000 | -0.000 | -0.000 |
| 133.765 | 237.971 | 111.578 | 0.000 | -0.000 | -0.000 |
| 133.120 | 111.939 | 242.316 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 92.444 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 117.883 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 116.246 |
| 244.819 | 133.690 | 134.591 | -0.000 | 0.000 | 0.000 |
| 133.765 | 237.971 | 111.579 | -0.000 | 0.000 | 0.000 |
| 133.120 | 111.939 | 242.316 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 92.444 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 115.812 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 119.739 |
| 247.282 | 136.868 | 135.147 | 0.000 | -0.000 | -0.000 |
| 136.868 | 242.481 | 111.447 | 0.000 | -0.000 | -0.000 |
| 133.120 | 111.939 | 242.316 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 92.444 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 115.812 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 119.739 |
| 247.283 | 136.869 | 135.148 | -0.000 | 0.000 | 0.000 |
| 133.765 | 237.971 | 111.579 | -0.000 | 0.000 | 0.000 |
| 133.120 | 111.939 | 242.316 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 93.369 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.001 | -0.000 | 115.812 | 0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | 0.000 | 116.246 |
| 244.588 | 134.045 | 133.464 | 0.000 | -0.000 | -0.000 |
| 134.045 | 237.829 | 112.468 | 0.000 | -0.000 | -0.000 |
| 133.119 | 111.939 | 242.315 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 93.369 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.001 | 0.000 | 115.812 | -0.000 |
| -0.000 | -0.001 | -0.000 | 0.000 | -0.000 | 116.246 |
| 242.336 | 148.914 | 84.989 | 0.000 | 0.000 | 0.000 |
| 148.914 | 242.336 | 84.989 | 0.000 | -0.000 | 0.000 |
| 142.849 | 142.849 | 215.301 | 0.000 | -0.000 | 0.000 |
| 1.101 | 1.101 | -58.610 | 109.011 | -0.000 | 0.000 |
| 1.101 | 1.101 | -58.610 | 0.000 | 109.011 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 110.983 |
| 252.103 | 137.368 | 142.790 | -0.000 | 0.000 | -0.000 |
| 137.368 | 252.103 | 142.790 | -0.000 | 0.000 | -0.000 |
| 142.849 | 142.849 | 215.301 | -0.000 | -0.000 | -0.000 |
| -1.101 | -1.101 | 58.610 | 109.011 | 0.000 | -0.000 |
| -1.101 | -1.101 | 58.610 | -0.000 | 109.011 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 110.983 |
| 242.022 | 147.340 | 138.038 | 0.000 | -0.000 | 0.000 |
| 147.340 | 242.022 | 138.038 | 0.000 | -0.000 | 0.000 |
| 143.879 | 143.879 | 195.919 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 115.698 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 115.698 | 0.000 |
| 0.111 | 0.111 | -5.850 | 0.000 | -0.000 | 110.983 |
| 252.103 | 137.367 | 142.790 | -0.000 | 0.000 | -0.000 |
| 137.367 | 252.103 | 142.790 | -0.000 | 0.000 | -0.000 |
| 142.849 | 142.849 | 215.301 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 115.698 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 115.698 | -0.000 |
| -0.111 | -0.111 | 5.850 | -0.000 | 0.000 | 110.983 |
| 252.103 | 137.368 | 142.791 | 0.000 | -0.000 | 0.000 |
| 137.368 | 252.103 | 142.791 | 0.000 | -0.000 | 0.000 |
| 145.642 | 145.642 | 187.702 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 115.698 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 115.698 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 110.983 |
| 242.232 | 146.921 | 144.062 | -0.000 | 0.000 | -0.000 |
| 146.921 | 242.232 | 144.062 | -0.000 | -0.000 | -0.000 |
| 144.041 | 144.041 | 199.207 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 115.698 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 115.698 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 110.983 |
| 252.161 | 136.870 | 143.042 | -0.000 | -0.000 | -0.000 |
| 136.870 | 252.161 | 143.042 | -0.000 | -0.000 | 0.000 |
| 158.396 | 158.396 | 257.840 | -0.000 | -0.000 | -0.000 |
| 14.824 | 14.824 | 50.321 | 107.531 | -0.000 | -0.000 |
| 14.824 | 14.824 | 50.321 | -0.000 | 107.531 | -0.000 |
| 14.829 | 14.829 | 50.339 | -0.000 | -0.000 | 110.652 |
| 252.161 | 136.870 | 143.042 | 0.000 | 0.000 | -0.000 |
| 136.870 | 252.161 | 143.042 | 0.000 | 0.000 | -0.000 |
| 143.043 | 143.043 | 215.999 | 0.000 | 0.000 | -0.000 |
| -14.824 | -14.824 | -50.321 | 107.531 | 0.000 | 0.000 |
| -14.824 | -14.824 | -50.321 | 0.000 | 107.531 | 0.000 |
| -14.829 | -14.829 | -50.339 | 0.000 | 0.000 | 110.652 |
| 243.755 | 147.491 | 151.035 | -0.000 | -0.000 | -0.000 |
| 147.491 | 243.755 | 151.035 | 0.000 | -0.000 | 0.000 |
| 143.043 | 143.043 | 215.999 | -0.000 | -0.000 | 0.000 |
| 1.283 | 1.283 | 6.914 | 110.035 | -0.000 | 0.000 |
| 1.283 | 1.283 | 6.914 | -0.000 | 110.035 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 110.652 |
| 252.161 | 136.870 | 143.042 | -0.000 | 0.000 | 0.000 |
| 136.870 | 252.161 | 143.042 | 0.000 | 0.000 | -0.000 |
| 142.817 | 142.817 | 195.592 | 0.000 | 0.000 | 0.000 |
| -1.283 | -1.283 | -6.914 | 110.035 | 0.000 | 0.000 |
| -1.283 | -1.283 | -6.914 | 0.000 | 110.035 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 110.652 |
| 242.535 | 146.556 | 144.341 | -0.000 | -0.000 | 0.000 |
| 146.556 | 242.535 | 144.341 | -0.000 | -0.000 | 0.000 |
| 143.043 | 143.043 | 215.999 | -0.000 | -0.000 | 0.000 |
| 0.141 | 0.141 | 1.256 | 107.645 | -0.000 | 0.000 |
| 0.141 | 0.141 | 1.256 | 0.000 | 107.645 | -0.000 |
| 0.124 | 0.124 | 0.704 | -0.000 | -0.000 | 110.652 |
| 242.085 | 146.419 | 143.269 | 0.000 | 0.000 | -0.000 |
| 146.419 | 242.085 | 143.269 | 0.000 | 0.000 | -0.000 |
| 143.780 | 143.780 | 200.833 | 0.000 | 0.000 | 0.000 |
| -0.141 | -0.141 | -1.256 | 107.645 | 0.000 | 0.000 |
| -0.141 | -0.141 | -1.256 | 0.000 | 107.645 | -0.000 |
| -0.124 | -0.124 | -0.704 | 0.000 | 0.000 | 110.652 |
| 252.161 | 136.859 | 143.046 | 0.000 | -0.000 | -0.000 |
| 136.859 | 252.161 | 143.046 | -0.000 | 0.000 | -0.000 |
| 143.046 | 143.046 | 216.011 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 116.017 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 116.017 | 0.000 |
| 3.369 | 3.369 | -8.268 | -0.000 | 0.000 | 110.643 |
| 240.346 | 141.697 | 152.118 | -0.000 | 0.000 | -0.000 |
| 141.697 | 240.346 | 152.118 | -0.000 | -0.000 | -0.000 |
| 139.998 | 139.998 | 215.726 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 116.017 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 116.017 | 0.000 |
| -3.369 | -3.369 | 8.268 | 0.000 | -0.000 | 110.643 |
| 242.524 | 146.840 | 143.105 | 0.000 | 0.000 | 0.000 |
| 146.840 | 242.524 | 143.105 | 0.000 | 0.000 | -0.000 |
| 143.046 | 143.046 | 216.011 | 0.000 | 0.000 | -0.000 |
| 0.352 | 0.352 | -1.216 | 106.043 | -0.000 | -0.000 |
| 0.352 | 0.352 | -1.216 | 0.000 | 106.043 | -0.000 |
| 0.356 | 0.356 | -0.707 | 0.000 | 0.000 | 110.643 |
| 252.161 | 136.859 | 143.046 | -0.000 | -0.000 | 0.000 |
| 136.859 | 252.161 | 143.046 | -0.000 | -0.000 | -0.000 |
| 143.046 | 143.046 | 216.010 | -0.000 | -0.000 | -0.000 |
| -0.352 | -0.352 | 1.216 | 106.043 | 0.000 | -0.000 |
| -0.352 | -0.352 | 1.216 | -0.000 | 106.043 | 0.000 |
| -0.356 | -0.356 | 0.707 | 0.000 | -0.000 | 110.643 |
| 242.201 | 146.611 | 143.952 | 0.000 | 0.000 | 0.000 |
| 146.611 | 242.201 | 143.952 | 0.000 | 0.000 | 0.000 |
| 144.192 | 144.192 | 200.411 | -0.000 | 0.000 | -0.000 |
| 0.027 | 0.027 | -0.052 | 110.433 | 0.000 | 0.000 |
| 0.027 | 0.027 | -0.052 | 0.000 | 110.433 | 0.000 |
| 0.034 | 0.034 | -0.083 | -0.000 | 0.000 | 110.643 |
| 252.160 | 136.859 | 143.046 | -0.000 | -0.000 | 0.000 |
| 136.859 | 252.160 | 143.046 | -0.000 | -0.000 | 0.000 |
| 145.207 | 145.207 | 192.986 | -0.000 | -0.000 | -0.000 |
| -0.027 | -0.027 | 0.052 | 110.433 | -0.000 | 0.000 |
| -0.027 | -0.027 | 0.052 | 0.000 | 110.433 | -0.000 |
| -0.034 | -0.034 | 0.083 | 0.000 | -0.000 | 110.643 |
| 232.699 | 149.476 | 149.476 | 0.000 | 0.000 | 0.000 |
| 149.476 | 232.699 | 149.476 | 0.000 | 0.000 | 0.000 |
| 149.476 | 149.476 | 232.699 | 0.000 | 0.000 | 0.000 |
| -18.436 | -18.436 | -18.436 | 104.319 | 0.000 | 0.000 |
| -18.436 | -18.436 | -18.436 | 0.000 | 104.319 | 0.000 |
| -18.436 | -18.436 | -18.436 | -0.000 | 0.000 | 104.319 |
| 254.733 | 167.724 | 167.724 | -0.000 | -0.000 | -0.000 |
| 167.724 | 254.733 | 167.724 | -0.000 | -0.000 | -0.000 |
| 167.724 | 167.724 | 254.733 | 0.000 | 0.000 | -0.000 |
| 18.436 | 18.436 | 18.436 | 104.319 | -0.000 | -0.000 |
| 18.436 | 18.436 | 18.436 | -0.000 | 104.319 | -0.000 |
| 18.436 | 18.436 | 18.436 | 0.000 | -0.000 | 104.319 |
| 246.270 | 167.644 | 167.644 | -0.000 | 0.000 | 0.000 |
| 167.644 | 246.270 | 167.644 | -0.000 | 0.000 | 0.000 |
| 167.644 | 167.644 | 246.270 | 0.000 | 0.000 | 0.000 |
| -1.787 | -1.787 | -1.787 | 95.581 | 0.000 | 0.000 |
| -1.787 | -1.787 | -1.787 | 0.000 | 95.581 | 0.000 |
| -1.787 | -1.787 | -1.787 | 0.000 | 0.000 | 95.581 |
| 249.759 | 170.901 | 170.901 | -0.000 | -0.000 | -0.000 |
| 170.901 | 249.759 | 170.901 | -0.000 | 0.000 | -0.000 |
| 170.901 | 170.901 | 249.759 | 0.000 | -0.000 | -0.000 |
| 1.787 | 1.787 | 1.787 | 95.581 | -0.000 | -0.000 |
| 1.787 | 1.787 | 1.787 | -0.000 | 95.581 | -0.000 |
| 1.787 | 1.787 | 1.787 | 0.000 | -0.000 | 95.581 |
| 254.734 | 167.724 | 167.724 | 0.000 | 0.000 | 0.000 |
| 167.724 | 254.734 | 167.724 | 0.000 | 0.000 | 0.000 |
| 167.724 | 167.724 | 254.734 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 107.098 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 107.098 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 107.098 |
| 250.040 | 168.049 | 168.049 | 0.000 | -0.000 | -0.000 |
| 168.049 | 250.040 | 168.049 | 0.000 | -0.000 | -0.000 |
| 168.049 | 168.049 | 250.040 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 107.098 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 107.098 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 107.098 |
| 254.767 | 167.734 | 167.734 | 0.000 | 0.000 | -0.000 |
| 167.734 | 254.767 | 167.734 | -0.000 | 0.000 | -0.000 |
| 167.734 | 167.734 | 254.767 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 107.128 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 107.128 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 107.128 |
| 254.767 | 167.734 | 167.734 | -0.000 | -0.000 | 0.000 |
| 167.734 | 254.767 | 167.734 | -0.000 | 0.000 | 0.000 |
| 167.734 | 167.734 | 254.767 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 107.128 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 107.128 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 107.128 |
| 254.767 | 167.734 | 167.734 | 0.000 | 0.000 | -0.000 |
| 167.734 | 254.767 | 167.734 | 0.000 | 0.000 | -0.000 |
| 167.734 | 167.734 | 254.767 | -0.000 | -0.000 | -0.000 |
| -2.887 | -2.887 | -2.887 | 103.088 | -0.000 | -0.000 |
| -2.887 | -2.887 | -2.887 | -0.000 | 103.088 | -0.000 |
| -2.887 | -2.887 | -2.887 | -0.000 | -0.000 | 103.088 |
| 254.766 | 167.734 | 167.734 | -0.000 | -0.000 | 0.000 |
| 167.734 | 254.766 | 167.734 | 0.000 | -0.000 | 0.000 |
| 167.734 | 167.734 | 254.766 | -0.000 | 0.000 | 0.000 |
| 2.887 | 2.887 | 2.887 | 103.088 | 0.000 | 0.000 |
| 2.887 | 2.887 | 2.887 | 0.000 | 103.088 | 0.000 |
| 2.887 | 2.887 | 2.887 | -0.000 | 0.000 | 103.088 |
| 249.892 | 167.568 | 167.568 | 0.000 | -0.000 | -0.000 |
| 167.568 | 249.892 | 167.568 | 0.000 | -0.000 | -0.000 |
| 167.568 | 167.568 | 249.892 | -0.000 | 0.000 | -0.000 |
| -0.631 | -0.631 | -0.631 | 98.300 | -0.000 | -0.000 |
| -0.631 | -0.631 | -0.631 | -0.000 | 98.300 | -0.000 |
| -0.631 | -0.631 | -0.631 | -0.000 | -0.000 | 98.300 |
| 250.081 | 168.081 | 168.081 | -0.000 | 0.000 | 0.000 |
| 168.081 | 250.081 | 168.081 | -0.000 | 0.000 | 0.000 |
| 168.081 | 168.081 | 250.081 | 0.000 | -0.000 | 0.000 |
| 0.631 | 0.631 | 0.631 | 98.300 | 0.000 | 0.000 |
| 0.631 | 0.631 | 0.631 | -0.000 | 98.300 | 0.000 |
| 0.631 | 0.631 | 0.631 | 0.000 | 0.000 | 98.300 |
| 89.027 | 56.749 | 56.749 | 0.000 | -0.000 | -0.000 |
| 56.749 | 89.027 | 56.749 | 0.000 | 0.000 | -0.000 |
| 56.749 | 56.749 | 89.027 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -56.203 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -56.203 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -56.203 |
| 89.027 | 56.749 | 56.749 | -0.000 | -0.000 | 0.000 |
| 56.749 | 89.027 | 56.749 | -0.000 | 0.000 | 0.000 |
| 56.749 | 56.749 | 89.027 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -56.203 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -56.203 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -56.203 |
| 89.027 | 56.749 | 56.749 | 0.000 | 0.000 | -0.000 |
| 56.749 | 89.027 | 56.749 | 0.000 | -0.000 | -0.000 |
| 56.749 | 56.749 | 89.027 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -56.203 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -56.203 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -56.203 |
| 89.027 | 56.749 | 56.749 | -0.000 | -0.000 | 0.000 |
| 56.749 | 89.027 | 56.749 | 0.000 | 0.000 | 0.000 |
| 56.749 | 56.749 | 89.027 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -56.203 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -56.203 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -56.203 |
| 89.027 | 56.749 | 56.749 | 0.000 | -0.000 | -0.000 |
| 56.749 | 89.027 | 56.749 | 0.000 | -0.000 | -0.000 |
| 56.749 | 56.749 | 89.027 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -56.203 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -56.203 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -56.203 |
| 89.026 | 56.750 | 56.750 | -0.000 | -0.000 | 0.000 |
| 56.750 | 89.026 | 56.750 | -0.000 | -0.000 | 0.000 |
| 56.750 | 56.750 | 89.026 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -56.203 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -56.203 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -56.203 |
| 182.346 | 123.647 | 123.647 | -0.000 | -0.000 | -0.000 |
| 123.647 | 182.346 | 123.647 | -0.000 | -0.000 | -0.000 |
| 123.647 | 123.647 | 182.346 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 31.038 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 31.038 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 31.038 |
| 182.346 | 123.647 | 123.647 | 0.000 | 0.000 | 0.000 |
| 123.647 | 182.346 | 123.647 | 0.000 | 0.000 | 0.000 |
| 123.647 | 123.647 | 182.346 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 31.038 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 31.038 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 31.038 |
| 182.346 | 123.647 | 123.647 | -0.000 | 0.000 | 0.000 |
| 123.647 | 182.346 | 123.647 | -0.000 | -0.000 | 0.000 |
| 123.647 | 123.647 | 182.346 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 31.038 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 31.038 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 31.038 |
| 182.346 | 123.647 | 123.647 | 0.000 | -0.000 | -0.000 |
| 123.647 | 182.346 | 123.647 | -0.000 | 0.000 | -0.000 |
| 123.647 | 123.647 | 182.346 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 31.038 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 31.038 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 31.038 |
| 182.345 | 123.647 | 123.647 | -0.000 | -0.000 | -0.000 |
| 123.647 | 182.345 | 123.647 | -0.000 | 0.000 | -0.000 |
| 123.647 | 123.647 | 182.345 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 31.038 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 31.038 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 31.038 |
| 182.348 | 123.647 | 123.647 | 0.000 | -0.000 | 0.000 |
| 123.647 | 182.348 | 123.647 | -0.000 | 0.000 | -0.000 |
| 123.647 | 123.647 | 182.348 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 31.038 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 31.038 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 31.038 |
| 112.038 | 116.998 | 116.998 | 0.000 | -0.000 | -0.000 |
| 116.998 | 112.038 | 116.998 | -0.000 | -0.000 | -0.000 |
| 116.998 | 116.998 | 112.038 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -9.863 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -9.863 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -9.863 |
| 112.038 | 116.998 | 116.998 | 0.000 | 0.000 | 0.000 |
| 116.998 | 112.038 | 116.998 | 0.000 | 0.000 | 0.000 |
| 116.998 | 116.998 | 112.038 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -9.863 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -9.863 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -9.863 |
| 112.038 | 116.998 | 116.998 | -0.000 | -0.000 | 0.000 |
| 116.998 | 112.038 | 116.998 | -0.000 | -0.000 | -0.000 |
| 116.998 | 116.998 | 112.038 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -9.863 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -9.863 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -9.863 |
| 112.038 | 116.998 | 116.998 | 0.000 | 0.000 | 0.000 |
| 116.998 | 112.038 | 116.998 | 0.000 | 0.000 | 0.000 |
| 116.998 | 116.998 | 112.038 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -9.863 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -9.863 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -9.863 |
| 112.039 | 116.998 | 116.998 | 0.000 | 0.000 | -0.000 |
| 116.998 | 112.039 | 116.998 | 0.000 | -0.000 | -0.000 |
| 116.998 | 116.998 | 112.039 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -9.863 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -9.863 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -9.863 |
| 112.037 | 116.997 | 116.997 | 0.000 | -0.000 | 0.000 |
| 116.997 | 112.037 | 116.997 | 0.000 | 0.000 | 0.000 |
| 116.997 | 116.997 | 112.037 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -9.863 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -9.863 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -9.863 |
| 51.391 | 46.478 | 46.478 | 0.000 | 0.000 | 0.000 |
| 46.478 | 51.391 | 46.478 | 0.000 | 0.000 | 0.000 |
| 46.478 | 46.478 | 51.391 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 2.885 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 2.885 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 2.885 |
| 51.391 | 46.478 | 46.478 | -0.000 | 0.000 | 0.000 |
| 46.478 | 51.391 | 46.478 | -0.000 | 0.000 | -0.000 |
| 46.478 | 46.478 | 51.391 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 2.885 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 2.885 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 2.885 |
| 51.391 | 46.478 | 46.478 | 0.000 | -0.000 | -0.000 |
| 46.478 | 51.391 | 46.478 | 0.000 | 0.000 | 0.000 |
| 46.478 | 46.478 | 51.391 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 2.885 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 2.885 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 2.885 |
| 51.391 | 46.478 | 46.478 | -0.000 | 0.000 | -0.000 |
| 46.478 | 51.391 | 46.478 | -0.000 | 0.000 | -0.000 |
| 46.478 | 46.478 | 51.391 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 2.885 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 2.885 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 2.885 |
| 51.391 | 46.478 | 46.478 | 0.000 | 0.000 | -0.000 |
| 46.478 | 51.391 | 46.478 | 0.000 | 0.000 | -0.000 |
| 46.478 | 46.478 | 51.391 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 2.885 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 2.885 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 2.885 |
| 51.391 | 46.477 | 46.477 | -0.000 | -0.000 | 0.000 |
| 46.477 | 51.391 | 46.477 | -0.000 | 0.000 | 0.000 |
| 46.477 | 46.477 | 51.391 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 2.885 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 2.885 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 2.885 |
| 293.596 | 69.144 | 69.144 | 0.000 | -0.000 | -0.000 |
| 69.144 | 293.596 | 69.144 | 0.000 | -0.000 | -0.000 |
| 69.144 | 69.144 | 293.596 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 30.947 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 30.947 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 30.947 |
| 293.596 | 69.144 | 69.144 | -0.000 | 0.000 | 0.000 |
| 69.144 | 293.596 | 69.144 | -0.000 | -0.000 | 0.000 |
| 69.144 | 69.144 | 293.596 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 30.947 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 30.947 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 30.947 |
| 293.596 | 69.144 | 69.144 | -0.000 | 0.000 | -0.000 |
| 69.144 | 293.596 | 69.144 | 0.000 | 0.000 | -0.000 |
| 69.144 | 69.144 | 293.596 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 30.947 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 30.947 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 30.947 |
| 293.596 | 69.144 | 69.144 | -0.000 | -0.000 | 0.000 |
| 69.144 | 293.596 | 69.144 | -0.000 | 0.000 | 0.000 |
| 69.144 | 69.144 | 293.596 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 30.947 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 30.947 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 30.947 |
| 293.598 | 69.144 | 69.144 | 0.000 | -0.000 | -0.000 |
| 69.144 | 293.598 | 69.144 | 0.000 | -0.000 | -0.000 |
| 69.144 | 69.144 | 293.598 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -1.455 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -1.455 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -1.455 |
| 293.594 | 69.143 | 69.143 | -0.000 | -0.000 | 0.000 |
| 69.143 | 293.594 | 69.143 | -0.000 | -0.000 | 0.000 |
| 69.143 | 69.143 | 293.594 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -1.455 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -1.455 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -1.455 |
| 95.943 | 51.197 | 51.197 | -0.000 | -0.000 | -0.000 |
| 51.197 | 95.943 | 51.197 | -0.000 | -0.000 | 0.000 |
| 51.197 | 51.197 | 95.943 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 19.304 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 19.304 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 19.304 |
| 99.769 | 49.284 | 49.284 | -0.000 | 0.000 | 0.000 |
| 49.284 | 99.769 | 49.284 | -0.000 | 0.000 | -0.000 |
| 49.284 | 49.284 | 99.769 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 19.304 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.304 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 19.304 |
| 95.943 | 51.197 | 51.197 | 0.000 | 0.000 | -0.000 |
| 51.197 | 95.943 | 51.197 | -0.000 | -0.000 | -0.000 |
| 51.197 | 51.197 | 95.943 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 19.304 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 19.304 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 19.304 |
| 99.769 | 49.284 | 49.284 | 0.000 | 0.000 | 0.000 |
| 49.284 | 99.769 | 49.284 | 0.000 | 0.000 | -0.000 |
| 49.284 | 49.284 | 99.769 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 19.304 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.304 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 19.304 |
| 99.769 | 49.284 | 49.284 | 0.000 | -0.000 | -0.000 |
| 49.284 | 99.769 | 49.284 | -0.000 | -0.000 | 0.000 |
| 49.284 | 49.284 | 99.769 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 19.304 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 19.304 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 19.304 |
| 95.943 | 51.197 | 51.197 | -0.000 | 0.000 | 0.000 |
| 51.197 | 95.943 | 51.197 | -0.000 | -0.000 | 0.000 |
| 51.197 | 51.197 | 95.943 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 19.304 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 19.304 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 19.304 |
| 43.819 | 51.336 | 51.336 | 0.000 | 0.000 | 0.000 |
| 51.336 | 43.819 | 51.336 | 0.000 | 0.000 | 0.000 |
| 51.336 | 51.336 | 43.819 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 23.317 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 23.317 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 23.317 |
| 43.819 | 51.336 | 51.336 | -0.000 | -0.000 | -0.000 |
| 51.336 | 43.819 | 51.336 | -0.000 | -0.000 | -0.000 |
| 51.336 | 51.336 | 43.819 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 23.317 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 23.317 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 23.317 |
| 43.819 | 51.336 | 51.336 | 0.000 | 0.000 | 0.000 |
| 51.336 | 43.819 | 51.336 | 0.000 | 0.000 | 0.000 |
| 51.336 | 51.336 | 43.819 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 12.443 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 12.443 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 12.443 |
| 43.819 | 51.336 | 51.336 | -0.000 | -0.000 | -0.000 |
| 51.336 | 43.819 | 51.336 | -0.000 | -0.000 | -0.000 |
| 51.336 | 51.336 | 43.819 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 12.443 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 12.443 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 12.443 |
| 43.820 | 51.336 | 51.336 | 0.000 | 0.000 | 0.000 |
| 51.336 | 43.820 | 51.336 | 0.000 | 0.000 | 0.000 |
| 51.336 | 51.336 | 43.820 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 12.443 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 12.443 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 12.443 |
| 43.819 | 51.336 | 51.336 | -0.000 | -0.000 | -0.000 |
| 51.336 | 43.819 | 51.336 | -0.000 | -0.000 | -0.000 |
| 51.336 | 51.336 | 43.819 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 12.443 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 12.443 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 12.443 |
| 63.937 | 47.115 | 47.115 | -0.000 | -0.000 | 0.000 |
| 47.115 | 63.937 | 47.115 | -0.000 | -0.000 | 0.000 |
| 47.115 | 47.115 | 63.937 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 18.105 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 18.105 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 18.105 |
| 63.937 | 47.115 | 47.115 | 0.000 | 0.000 | -0.000 |
| 47.115 | 63.937 | 47.115 | 0.000 | 0.000 | 0.000 |
| 47.115 | 47.115 | 63.937 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 18.105 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 18.105 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 18.105 |
| 63.937 | 47.115 | 47.115 | -0.000 | 0.000 | 0.000 |
| 47.115 | 63.937 | 47.115 | -0.000 | 0.000 | 0.000 |
| 47.115 | 47.115 | 63.937 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 18.105 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 18.105 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 18.105 |
| 63.937 | 47.115 | 47.115 | 0.000 | -0.000 | 0.000 |
| 47.115 | 63.937 | 47.115 | -0.000 | -0.000 | -0.000 |
| 47.115 | 47.115 | 63.937 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 18.105 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 18.105 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 18.105 |
| 63.937 | 47.115 | 47.115 | -0.000 | 0.000 | -0.000 |
| 47.115 | 63.937 | 47.115 | -0.000 | -0.000 | -0.000 |
| 47.115 | 47.115 | 63.937 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 18.105 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 18.105 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 18.105 |
| 63.938 | 47.115 | 47.115 | 0.000 | -0.000 | -0.000 |
| 47.115 | 63.938 | 47.115 | -0.000 | -0.000 | -0.000 |
| 47.115 | 47.115 | 63.938 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 18.105 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 18.105 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 18.105 |
| 34.855 | 22.794 | 22.794 | -0.000 | -0.000 | 0.000 |
| 22.794 | 34.855 | 22.794 | 0.000 | -0.000 | 0.000 |
| 22.794 | 22.794 | 34.855 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 1.914 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 1.914 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.914 |
| 34.855 | 22.794 | 22.794 | 0.000 | 0.000 | -0.000 |
| 22.794 | 34.855 | 22.794 | -0.000 | 0.000 | -0.000 |
| 22.794 | 22.794 | 34.855 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 1.914 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 1.914 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 1.914 |
| 34.855 | 22.794 | 22.794 | 0.000 | -0.000 | 0.000 |
| 22.794 | 34.855 | 22.794 | 0.000 | 0.000 | 0.000 |
| 22.794 | 22.794 | 34.855 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 8.443 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 8.444 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 8.444 |
| 12.120 | 0.421 | 0.421 | -0.000 | 0.000 | -0.000 |
| 0.421 | 12.120 | 0.421 | -0.000 | 0.000 | -0.000 |
| 0.421 | 0.421 | 12.120 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 8.444 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 8.444 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 8.444 |
| 12.117 | 0.460 | 0.460 | 0.000 | -0.000 | 0.000 |
| 0.460 | 12.117 | 0.460 | 0.000 | 0.000 | 0.000 |
| 0.460 | 0.460 | 12.117 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 1.914 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 1.914 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 1.914 |
| 12.120 | 0.421 | 0.421 | 0.000 | 0.000 | -0.000 |
| 0.421 | 12.120 | 0.421 | -0.000 | 0.000 | -0.000 |
| 0.421 | 0.421 | 12.120 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 1.914 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 1.914 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 1.914 |
| 32450456.243 | 23323729.516 | 36861395.958 | -676434.741 | -243616.371 | 35581.530 |
| 32039941.681 | 23585100.688 | 36857964.647 | -775583.047 | -11634.733 | -110567.544 |
| 32421552.166 | 23784587.357 | 37519315.574 | -533155.256 | -319280.669 | -188116.923 |
| 32011702.964 | 23437322.322 | 36478454.836 | -670293.804 | 11565.620 | -244751.662 |
| 31761191.123 | 23445761.352 | 36408807.747 | -529699.257 | -159056.002 | -78097.798 |
| 32293224.625 | 23721921.085 | 37260956.428 | -702060.836 | -261242.727 | -158799.418 |
| -31687715.322 | -23240241.009 | -36494467.410 | 672718.979 | 290523.282 | 258066.456 |
| -32250788.270 | -23935840.563 | -36958591.755 | 710474.662 | 71588.227 | 309587.839 |
| -31998982.109 | -23395577.491 | -36542119.818 | 727576.023 | 125278.031 | 191067.949 |
| -32071337.192 | -23669238.855 | -36959815.537 | 711227.564 | 95759.973 | 54881.896 |
| -31389107.081 | -23284018.664 | -36268489.987 | 724112.949 | 78249.375 | 24219.445 |
| -32377878.631 | -23595717.185 | -37156759.509 | 544324.291 | 33844.682 | 88992.547 |
| 3202371.111 | 2370512.927 | 3703360.502 | -66328.875 | -30902.069 | -9061.857 |
| 3216009.374 | 2342034.551 | 3688139.633 | -64757.478 | 5126.285 | 19705.967 |
| 3249319.141 | 2387939.051 | 3746228.970 | -69304.240 | -17157.796 | -4953.869 |
| 3196515.725 | 2360521.917 | 3678177.870 | -78594.467 | -19718.957 | 1654.106 |
| 3160258.963 | 2333587.245 | 3659223.332 | -57818.055 | -16579.103 | 812.351 |
| 3256243.974 | 2394448.562 | 3746362.599 | -70420.830 | -7209.573 | -23165.148 |
| -3214188.322 | -2362454.441 | -3682429.660 | 65630.222 | 13767.731 | 24122.905 |
| -3205064.279 | -2378395.161 | -3699580.277 | 73972.772 | 17436.847 | 12995.769 |
| -3206801.498 | -2374158.800 | -3698992.824 | 72547.656 | 24173.348 | 20389.480 |
| -3211351.703 | -2369395.854 | -3694333.415 | 51966.450 | 8079.513 | 15856.777 |
| -3221102.955 | -2379351.732 | -3715363.167 | 54910.686 | 14618.978 | -3347.814 |
| -3214233.921 | -2383634.425 | -3725536.148 | 64986.024 | 35027.212 | 1455.902 |
| 323071.376 | 238810.024 | 373760.735 | -7440.542 | -2996.055 | -2058.936 |
| 323463.346 | 239410.581 | 372271.898 | -6819.421 | -1901.431 | 230.260 |
| 322036.252 | 236064.762 | 372538.711 | -6349.648 | -1433.242 | -401.954 |
| 324253.201 | 237011.476 | 370261.656 | -7152.504 | -1515.178 | -2509.107 |
| 321584.040 | 238094.588 | 369835.727 | -7240.963 | -2333.352 | -2655.042 |
| 318563.320 | 234223.774 | 365123.961 | -7790.837 | -2019.757 | -989.941 |
| -322727.771 | -236635.518 | -367944.878 | 6201.990 | 569.773 | 2160.804 |
| -322430.626 | -234612.102 | -366629.892 | 7460.292 | -105.949 | -1092.879 |
| -323739.630 | -237517.093 | -371057.328 | 6838.578 | 2483.783 | 1470.771 |
| -325783.768 | -235036.095 | -370670.929 | 6373.669 | 1212.650 | 2411.753 |
| -319781.538 | -237943.007 | -374581.329 | 6196.666 | 2418.669 | 1224.238 |
| -319694.591 | -238171.354 | -370794.084 | 5750.043 | 1561.065 | 669.943 |
| 85562145.358 | 30826795.313 | 52509890.681 | 386402.040 | -861511.589 | 1368248.680 |
| 85683554.995 | 31566587.223 | 52803026.351 | 577278.396 | 41864.406 | 1663796.456 |
| 85672905.316 | 31094840.456 | 53053910.716 | 353153.228 | 97327.010 | 1841117.392 |
| 85816164.686 | 31553145.553 | 52276557.599 | 511930.471 | -326542.881 | 1601686.655 |
| 84977904.380 | 31227310.421 | 52169789.005 | 47907.253 | -1041526.791 | 1646329.946 |
| 86162541.464 | 32218924.115 | 52900443.396 | -57445.857 | -649446.110 | 1537064.839 |
| -86413941.357 | -31226196.126 | -52787449.724 | 50005.386 | 345076.148 | -1766878.322 |
| -85547344.443 | -31416705.005 | -53073759.369 | -217069.459 | 671552.406 | -1720755.896 |
| -85268557.607 | -30837588.050 | -52517255.094 | -121868.952 | 357454.829 | -1478672.553 |
| -85594077.613 | -31606524.945 | -52816345.774 | -960.057 | 740861.557 | -1609801.163 |
| -85242590.349 | -31302225.115 | -52615317.327 | -289791.961 | 549713.670 | -1679098.847 |
| -85548846.077 | -31158571.483 | -53244608.646 | 239992.760 | 41149.445 | -1576129.469 |
| 8615867.706 | 3144748.849 | 5303990.816 | -1754.540 | -26901.807 | 127460.198 |
| 8533545.396 | 3116803.959 | 5206882.482 | 8799.123 | -22093.003 | 172680.688 |
| 8564073.511 | 3089287.254 | 5301001.545 | 20534.079 | -71833.104 | 158553.176 |
| 8641009.934 | 3146194.454 | 5277308.954 | 49435.948 | -860.611 | 196133.506 |
| 8527079.494 | 3128434.932 | 5252798.352 | -1261.980 | -58076.649 | 161715.576 |
| 8436848.099 | 3114794.853 | 5270417.095 | -9703.730 | -33133.588 | 159804.271 |
| -8457375.308 | -3059624.150 | -5261504.208 | 44694.492 | 66686.300 | -141585.360 |
| -8460288.764 | -3107955.786 | -5248124.425 | -18705.190 | 66527.754 | -169433.869 |
| -8561499.089 | -3104904.456 | -5330595.511 | 31268.006 | 44509.140 | -136397.058 |
| -8515112.284 | -3106685.370 | -5220439.059 | 22345.341 | 6720.841 | -153540.179 |
| -8535300.929 | -3162067.211 | -5316421.295 | 4364.442 | 54655.490 | -132698.012 |
| -8419462.901 | -3075250.833 | -5269623.310 | -49612.488 | 36527.726 | -138334.196 |
| 866463.388 | 316842.919 | 539027.377 | 2093.462 | -3057.213 | 15718.589 |
| 854608.561 | 308727.050 | 524307.369 | 244.733 | -6168.755 | 16130.454 |
| 851920.117 | 308380.799 | 536024.962 | 730.153 | -6647.344 | 21290.876 |
| 851348.528 | 310486.628 | 532503.123 | -923.769 | -2881.555 | 15142.094 |
| 866102.355 | 315709.333 | 532135.111 | -1489.953 | -3463.682 | 15698.855 |
| 847097.526 | 308428.353 | 525606.562 | -1169.963 | -6611.257 | 20136.125 |
| -850876.836 | -311472.991 | -527481.690 | -75.723 | 2310.287 | -16996.667 |
| -853122.052 | -312988.533 | -534930.302 | 1908.543 | 3830.270 | -14181.549 |
| -848944.372 | -313554.353 | -531741.510 | -5890.115 | 3477.741 | -20147.444 |
| -860746.663 | -315243.829 | -526906.347 | 251.491 | 6676.061 | -15716.119 |
| -856176.122 | -311055.925 | -533260.567 | -957.928 | 10284.855 | -16326.948 |
| -861638.528 | -311792.670 | -531703.217 | 2999.851 | 3083.932 | -13183.107 |
| 64.548 | 61.863 | 52.673 | 0.000 | 0.000 | -0.000 |
| 61.863 | 64.548 | 52.673 | 0.000 | 0.000 | -0.000 |
| 52.673 | 52.673 | 72.893 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 23.282 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 23.282 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 22.538 |
| 64.548 | 61.863 | 52.673 | -0.000 | -0.000 | 0.000 |
| 61.863 | 64.548 | 52.673 | -0.000 | -0.000 | 0.000 |
| 52.673 | 52.673 | 72.893 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 23.282 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 23.282 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 22.538 |
| 64.548 | 61.863 | 52.673 | 0.000 | 0.000 | -0.000 |
| 61.863 | 64.548 | 52.673 | 0.000 | 0.000 | -0.000 |
| 52.673 | 52.673 | 72.893 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 12.091 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 12.091 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 22.538 |
| 72.583 | 53.828 | 52.673 | -0.000 | -0.000 | 0.000 |
| 53.828 | 72.583 | 52.673 | -0.000 | -0.000 | 0.000 |
| 52.673 | 52.673 | 72.893 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 12.091 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 12.091 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 22.538 |
| 72.583 | 53.828 | 52.673 | 0.000 | 0.000 | -0.000 |
| 53.828 | 72.583 | 52.673 | 0.000 | 0.000 | -0.000 |
| 52.673 | 52.673 | 72.893 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 12.091 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 12.091 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 22.538 |
| 64.548 | 61.863 | 52.673 | -0.000 | -0.000 | 0.000 |
| 61.863 | 64.548 | 52.673 | -0.000 | -0.000 | -0.000 |
| 52.673 | 52.673 | 72.893 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 12.091 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 12.091 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 22.538 |
| 263.037 | 235.232 | 235.232 | -0.000 | -0.000 | -0.000 |
| 235.232 | 263.037 | 235.232 | -0.000 | 0.000 | -0.000 |
| 235.232 | 235.232 | 263.037 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 120.028 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 120.028 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 120.028 |
| 263.037 | 235.232 | 235.232 | 0.000 | 0.000 | 0.000 |
| 235.232 | 263.037 | 235.232 | 0.000 | 0.000 | -0.000 |
| 235.232 | 235.232 | 263.037 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 120.028 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 120.028 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 120.028 |
| 263.037 | 235.232 | 235.232 | -0.000 | 0.000 | -0.000 |
| 235.232 | 263.037 | 235.232 | -0.000 | -0.000 | 0.000 |
| 235.232 | 235.232 | 263.037 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -13.795 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -13.795 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -13.795 |
| 263.037 | 235.232 | 235.232 | 0.000 | 0.000 | 0.000 |
| 235.232 | 263.037 | 235.232 | 0.000 | 0.000 | 0.000 |
| 235.232 | 235.232 | 263.037 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -13.795 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -13.795 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -13.795 |
| 263.037 | 235.231 | 235.231 | -0.000 | -0.000 | -0.000 |
| 235.231 | 263.037 | 235.231 | -0.000 | 0.000 | -0.000 |
| 235.231 | 235.231 | 263.037 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -13.795 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -13.795 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -13.795 |
| 263.038 | 235.232 | 235.232 | 0.000 | 0.000 | 0.000 |
| 235.232 | 263.038 | 235.232 | 0.000 | -0.000 | 0.000 |
| 235.232 | 235.232 | 263.038 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -13.795 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -13.795 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -13.795 |
| 399.642 | 94.044 | 94.044 | 0.000 | 0.000 | -0.000 |
| 94.044 | 399.642 | 94.044 | 0.000 | 0.000 | -0.000 |
| 94.044 | 94.044 | 399.642 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 11.716 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 11.716 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 11.716 |
| 399.642 | 94.044 | 94.044 | -0.000 | -0.000 | 0.000 |
| 94.044 | 399.642 | 94.044 | -0.000 | -0.000 | 0.000 |
| 94.044 | 94.044 | 399.642 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 11.716 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 11.716 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 11.716 |
| 399.642 | 94.045 | 94.045 | 0.000 | -0.000 | -0.000 |
| 94.045 | 399.642 | 94.045 | 0.000 | 0.000 | -0.000 |
| 94.045 | 94.045 | 399.642 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 11.716 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 11.716 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 11.716 |
| 399.641 | 94.044 | 94.044 | -0.000 | -0.000 | 0.000 |
| 94.044 | 399.641 | 94.044 | -0.000 | -0.000 | 0.000 |
| 94.044 | 94.044 | 399.641 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 11.716 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 11.716 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 11.716 |
| 399.645 | 94.046 | 94.046 | 0.000 | 0.000 | -0.000 |
| 94.046 | 399.645 | 94.046 | 0.000 | 0.000 | -0.000 |
| 94.046 | 94.046 | 399.645 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 11.716 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 11.716 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 11.716 |
| 399.638 | 94.043 | 94.043 | -0.000 | -0.000 | 0.000 |
| 94.043 | 399.638 | 94.043 | -0.000 | 0.000 | 0.000 |
| 94.043 | 94.043 | 399.638 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 11.716 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 11.716 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 11.716 |
| 230.987 | 161.509 | 161.509 | -0.000 | 0.000 | 0.000 |
| 161.509 | 230.987 | 161.509 | 0.000 | 0.000 | 0.000 |
| 161.509 | 161.509 | 230.987 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 155.141 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 155.141 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 155.141 |
| 230.987 | 161.509 | 161.509 | -0.000 | 0.000 | 0.000 |
| 161.509 | 230.987 | 161.509 | -0.000 | 0.000 | 0.000 |
| 161.509 | 161.509 | 230.987 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 155.141 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 155.141 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 155.141 |
| 230.987 | 161.509 | 161.509 | 0.000 | 0.000 | -0.000 |
| 161.509 | 230.987 | 161.509 | 0.000 | -0.000 | -0.000 |
| 161.509 | 161.509 | 230.987 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 155.141 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 155.141 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 155.141 |
| 230.987 | 161.509 | 161.509 | -0.000 | 0.000 | 0.000 |
| 161.509 | 230.987 | 161.509 | -0.000 | -0.000 | 0.000 |
| 161.509 | 161.509 | 230.987 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 155.141 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 155.141 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 155.141 |
| 230.988 | 161.509 | 161.509 | 0.000 | 0.000 | 0.000 |
| 161.509 | 230.988 | 161.509 | 0.000 | 0.000 | 0.000 |
| 161.509 | 161.509 | 230.988 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 155.141 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 155.141 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 155.141 |
| 230.986 | 161.508 | 161.508 | -0.000 | 0.000 | -0.000 |
| 161.508 | 230.986 | 161.508 | -0.000 | -0.000 | -0.000 |
| 161.508 | 161.508 | 230.986 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 155.141 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 155.141 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 155.141 |
| 76.923 | 112.320 | 112.320 | 0.000 | 0.000 | 0.000 |
| 112.320 | 76.923 | 112.320 | 0.000 | 0.000 | 0.000 |
| 112.320 | 112.320 | 76.923 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 76.917 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 76.917 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 76.918 |
| 76.923 | 112.320 | 112.320 | -0.000 | -0.000 | -0.000 |
| 112.320 | 76.923 | 112.320 | -0.000 | -0.000 | -0.000 |
| 112.320 | 112.320 | 76.923 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 76.918 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 76.918 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 76.918 |
| 76.923 | 112.320 | 112.320 | 0.000 | 0.000 | 0.000 |
| 112.320 | 76.923 | 112.320 | 0.000 | 0.000 | 0.000 |
| 112.320 | 112.320 | 76.923 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -22.779 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -22.779 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -22.779 |
| 76.923 | 112.320 | 112.320 | -0.000 | -0.000 | -0.000 |
| 112.320 | 76.923 | 112.320 | -0.000 | -0.000 | -0.000 |
| 112.320 | 112.320 | 76.923 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -22.779 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -22.779 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -22.779 |
| 76.923 | 112.321 | 112.321 | 0.000 | 0.000 | 0.000 |
| 112.321 | 76.923 | 112.321 | 0.000 | 0.000 | 0.000 |
| 112.321 | 112.321 | 76.923 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -22.779 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -22.779 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -22.779 |
| 76.922 | 112.320 | 112.320 | -0.000 | -0.000 | -0.000 |
| 112.320 | 76.922 | 112.320 | -0.000 | -0.000 | -0.000 |
| 112.320 | 112.320 | 76.922 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -22.779 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -22.779 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -22.779 |
| 269.806 | 106.433 | 145.414 | 0.000 | 0.000 | 0.000 |
| 106.433 | 269.806 | 145.414 | 0.000 | 0.000 | 0.000 |
| 145.414 | 145.414 | 268.579 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 118.214 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 118.214 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 78.050 |
| 269.806 | 106.433 | 145.414 | -0.000 | -0.000 | -0.000 |
| 106.433 | 269.806 | 145.414 | -0.000 | -0.000 | -0.000 |
| 145.414 | 145.414 | 268.579 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 118.214 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 118.214 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 78.050 |
| 269.807 | 106.433 | 145.414 | 0.000 | -0.000 | 0.000 |
| 106.433 | 269.807 | 145.414 | 0.000 | 0.000 | 0.000 |
| 145.414 | 145.414 | 268.579 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 118.214 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 118.214 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 78.050 |
| 269.806 | 106.433 | 145.414 | -0.000 | -0.000 | -0.000 |
| 106.433 | 269.806 | 145.414 | -0.000 | -0.000 | -0.000 |
| 145.414 | 145.414 | 268.578 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 118.214 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 118.214 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 78.050 |
| 269.808 | 106.433 | 145.414 | 0.000 | 0.000 | 0.000 |
| 106.433 | 269.808 | 145.414 | 0.000 | 0.000 | 0.000 |
| 145.415 | 145.415 | 268.583 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.001 | 118.214 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.001 | 0.000 | 118.214 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 78.050 |
| 269.805 | 106.433 | 145.414 | -0.000 | -0.000 | -0.000 |
| 106.433 | 269.805 | 145.414 | -0.000 | -0.000 | -0.000 |
| 145.413 | 145.413 | 268.575 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.001 | 118.214 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.001 | -0.000 | 118.214 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 78.050 |
| 351.390 | 161.515 | 41.082 | 0.000 | 0.000 | 0.000 |
| 161.514 | 231.022 | 161.471 | 0.000 | 0.000 | 0.000 |
| 41.090 | 161.480 | 351.340 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 155.112 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 34.723 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 155.138 |
| 351.390 | 161.515 | 41.082 | 0.000 | -0.000 | -0.000 |
| 161.514 | 231.022 | 161.471 | 0.000 | -0.000 | -0.000 |
| 41.090 | 161.480 | 351.340 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 155.112 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 34.723 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 155.138 |
| 351.390 | 161.515 | 41.082 | 0.000 | 0.000 | 0.000 |
| 161.514 | 231.022 | 161.471 | 0.000 | 0.000 | 0.000 |
| 41.090 | 161.480 | 351.340 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 155.112 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 34.723 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 155.138 |
| 351.390 | 161.515 | 41.082 | 0.000 | 0.000 | -0.000 |
| 161.514 | 231.022 | 161.471 | -0.000 | -0.000 | -0.000 |
| 41.090 | 161.480 | 351.340 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 155.112 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 34.723 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 155.138 |
| 351.392 | 161.515 | 41.082 | -0.000 | 0.000 | 0.000 |
| 161.514 | 231.023 | 161.472 | -0.000 | 0.000 | 0.000 |
| 41.090 | 161.481 | 351.341 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.001 | 155.112 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 34.723 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 155.138 |
| 351.389 | 161.514 | 41.082 | -0.000 | -0.000 | -0.000 |
| 161.514 | 231.021 | 161.471 | -0.000 | 0.000 | -0.000 |
| 41.090 | 161.480 | 351.339 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.001 | 155.112 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 34.723 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 155.138 |
| 144.870 | 198.645 | 1.108 | -0.000 | -0.000 | -0.000 |
| 198.645 | 144.870 | 1.108 | -0.000 | 0.000 | -0.000 |
| 1.109 | 1.109 | 185.881 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -27.083 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -27.083 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 72.690 |
| 144.870 | 198.645 | 1.108 | 0.000 | 0.000 | 0.000 |
| 99.068 | 244.447 | 1.108 | 0.000 | 0.000 | 0.000 |
| 1.109 | 1.109 | 185.881 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -27.083 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -27.083 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 72.690 |
| 144.870 | 198.644 | 1.108 | -0.000 | -0.000 | -0.000 |
| 207.231 | 136.284 | 1.108 | 0.000 | 0.000 | -0.000 |
| 1.109 | 1.109 | 185.881 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -27.083 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -27.083 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -35.478 |
| 144.874 | 198.641 | 1.108 | 0.000 | 0.000 | 0.000 |
| 198.644 | 144.870 | 1.108 | 0.000 | 0.000 | 0.000 |
| 1.109 | 1.109 | 185.881 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -27.083 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -27.083 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -35.478 |
| 144.874 | 198.642 | 1.109 | -0.000 | -0.000 | -0.000 |
| -16098240.921 | -16098231.575 | 2756980.609 | 2.745 | -0.000 | 0.000 |
| 1.109 | 1.109 | 185.883 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -27.083 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -27.083 | -0.000 |
| -16098313.278 | -16098313.280 | 2756917.331 | -0.000 | -2.744 | 4.673 |
| 16098394.983 | 16098385.640 | -2756854.052 | -2.744 | -0.000 | -0.000 |
| 198.683 | 144.830 | 1.108 | 0.000 | 0.000 | 0.000 |
| 1.108 | 1.108 | 185.879 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -27.083 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -27.083 | 0.000 |
| 16098313.281 | 16098313.279 | -2756917.331 | 0.001 | -2.745 | 4.671 |
| 169.828 | 87.671 | 133.772 | -0.000 | -0.000 | -0.000 |
| 101.538 | 155.961 | 133.772 | 0.000 | 0.000 | -0.000 |
| 133.772 | 133.772 | 344.802 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 86.495 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 86.495 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 27.211 |
| 155.961 | 101.538 | 133.772 | -0.000 | -0.000 | -0.000 |
| 101.538 | 155.961 | 133.772 | 0.000 | -0.000 | 0.000 |
| 133.772 | 133.772 | 344.802 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 86.495 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 86.495 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 27.211 |
| 155.961 | 101.538 | 133.772 | -0.000 | 0.000 | -0.000 |
| 87.671 | 169.828 | 133.772 | -0.000 | -0.000 | -0.000 |
| 133.772 | 133.772 | 344.802 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 86.495 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 86.495 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 41.079 |
| 169.828 | 87.671 | 133.772 | 0.000 | 0.000 | 0.000 |
| 101.538 | 155.961 | 133.772 | 0.000 | -0.000 | 0.000 |
| 133.772 | 133.772 | 344.801 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 86.495 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 86.495 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 41.079 |
| 155.961 | 101.538 | 133.772 | -0.000 | 0.000 | -0.000 |
| 101.539 | 155.961 | 133.772 | -0.000 | 0.000 | -0.000 |
| 133.772 | 133.772 | 344.802 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 86.495 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 86.495 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 27.211 |
| 169.828 | 87.671 | 133.772 | 0.000 | -0.000 | 0.000 |
| 101.538 | 155.960 | 133.772 | -0.000 | -0.000 | 0.000 |
| 133.772 | 133.772 | 344.801 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 86.495 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 86.495 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 27.211 |
| 168.544 | 88.181 | 140.064 | -32.381 | -0.000 | 0.000 |
| 88.181 | 168.544 | 140.064 | 32.381 | -0.000 | 0.000 |
| 140.064 | 140.064 | 342.247 | -0.000 | -0.000 | 0.000 |
| -32.381 | 32.381 | 0.000 | 88.416 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 88.416 | -32.381 |
| -0.000 | 0.000 | 0.000 | -0.000 | -32.381 | 40.181 |
| 168.544 | 88.181 | 140.064 | -32.381 | 0.000 | -0.000 |
| 88.181 | 168.544 | 140.064 | 32.381 | 0.000 | -0.000 |
| 140.064 | 140.064 | 342.247 | 0.000 | 0.000 | -0.000 |
| -32.381 | 32.381 | -0.000 | 88.416 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 88.416 | -32.381 |
| 0.000 | -0.000 | -0.000 | 0.000 | -32.381 | 40.181 |
| 168.544 | 88.181 | 140.064 | -32.381 | -0.000 | 0.000 |
| 88.181 | 168.544 | 140.064 | 32.381 | -0.000 | 0.000 |
| 140.064 | 140.064 | 342.248 | -0.000 | -0.000 | 0.000 |
| -32.381 | 32.381 | 0.000 | 88.416 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 88.416 | -32.381 |
| -0.000 | 0.000 | 0.000 | -0.000 | -32.381 | 40.181 |
| 168.544 | 88.181 | 140.064 | -32.381 | 0.000 | -0.000 |
| 88.181 | 168.544 | 140.064 | 32.381 | 0.000 | -0.000 |
| 140.064 | 140.064 | 342.247 | 0.000 | 0.000 | -0.000 |
| -32.381 | 32.381 | -0.000 | 88.416 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 88.416 | -32.381 |
| 0.000 | -0.000 | -0.000 | 0.000 | -32.381 | 40.181 |
| 168.544 | 88.181 | 140.064 | -32.382 | -0.000 | 0.000 |
| 88.181 | 168.543 | 140.064 | 32.382 | -0.000 | 0.000 |
| 140.064 | 140.064 | 342.249 | -0.000 | -0.000 | 0.000 |
| -32.381 | 32.381 | 0.000 | 88.416 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 88.416 | -32.381 |
| -0.000 | 0.000 | 0.000 | -0.000 | -32.381 | 40.181 |
| 168.544 | 88.181 | 140.064 | -32.381 | 0.000 | -0.000 |
| 88.181 | 168.544 | 140.064 | 32.381 | 0.000 | -0.000 |
| 140.064 | 140.064 | 342.246 | 0.000 | 0.000 | -0.000 |
| -32.381 | 32.381 | -0.000 | 88.416 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 88.416 | -32.381 |
| 0.000 | -0.000 | -0.000 | 0.000 | -32.381 | 40.181 |
| 255.847 | 243.287 | 243.287 | -0.000 | 0.000 | 0.000 |
| 243.287 | 255.847 | 243.287 | -0.000 | 0.000 | 0.000 |
| 243.287 | 243.287 | 255.847 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 125.161 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 125.161 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 125.161 |
| 255.847 | 243.287 | 243.287 | 0.000 | -0.000 | 0.000 |
| 243.287 | 255.847 | 243.287 | 0.000 | -0.000 | -0.000 |
| 243.287 | 243.287 | 255.847 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 125.161 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 125.161 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 125.161 |
| 255.847 | 243.287 | 243.287 | -0.000 | 0.000 | 0.000 |
| 243.287 | 255.847 | 243.287 | -0.000 | -0.000 | 0.000 |
| 243.287 | 243.287 | 255.847 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 20.430 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 20.430 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 20.430 |
| 255.847 | 243.287 | 243.287 | 0.000 | 0.000 | -0.000 |
| 243.287 | 255.847 | 243.287 | 0.000 | -0.000 | -0.000 |
| 243.287 | 243.287 | 255.847 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 20.430 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 20.430 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 20.430 |
| 255.846 | 243.287 | 243.287 | -0.000 | 0.000 | -0.000 |
| 243.287 | 255.846 | 243.287 | -0.000 | -0.000 | 0.000 |
| 243.287 | 243.287 | 255.846 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 20.430 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 20.430 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 20.430 |
| 255.848 | 243.287 | 243.287 | 0.000 | 0.000 | 0.000 |
| 243.287 | 255.848 | 243.287 | 0.000 | 0.000 | -0.000 |
| 243.287 | 243.287 | 255.848 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 20.430 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 20.430 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 20.430 |
| 318.252 | 113.947 | 70.447 | -62.876 | 0.000 | 0.000 |
| 113.947 | 318.252 | 70.447 | 62.876 | 0.000 | 0.000 |
| 151.198 | 151.198 | 267.601 | -0.000 | 0.000 | 0.000 |
| 12.341 | 131.821 | -20.055 | 57.074 | 0.000 | 0.000 |
| 72.081 | 72.081 | -20.055 | -0.000 | 57.074 | -59.740 |
| 0.000 | -0.000 | 0.000 | 0.000 | -62.876 | 102.153 |
| 234.322 | 51.455 | 96.221 | -59.736 | -0.000 | -0.000 |
| 37.406 | 235.292 | 151.673 | 61.807 | -0.000 | -0.000 |
| -6.692 | -6.692 | 425.253 | -0.000 | -0.000 | -0.000 |
| -62.876 | 62.876 | 0.000 | 59.189 | -0.000 | -0.000 |
| -72.081 | -72.081 | 20.055 | 0.000 | 57.074 | -59.740 |
| 0.000 | 0.000 | 0.000 | 0.000 | -62.876 | 102.153 |
| 318.252 | 113.947 | 70.447 | -62.876 | 0.000 | 0.000 |
| 113.947 | 318.253 | 70.447 | 62.876 | 0.000 | 0.000 |
| 80.147 | 80.147 | 338.545 | -0.000 | 0.000 | 0.000 |
| -52.864 | 66.817 | -1.941 | 57.141 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 59.189 | -62.876 |
| 5.306 | 5.306 | -1.476 | -0.000 | -60.567 | 94.271 |
| 318.253 | 113.947 | 70.447 | -62.876 | -0.000 | -0.000 |
| 113.947 | 318.252 | 70.447 | 62.876 | -0.000 | -0.000 |
| 69.942 | 69.942 | 339.476 | 0.000 | -0.000 | -0.000 |
| -66.817 | 52.864 | 1.941 | 57.141 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 59.189 | -62.876 |
| -5.306 | -5.306 | 1.476 | 0.000 | -60.567 | 94.271 |
| 315.820 | 116.408 | 71.479 | -62.043 | 0.000 | -0.000 |
| 116.299 | 315.756 | 71.689 | 62.166 | 0.000 | 0.000 |
| 71.817 | 71.817 | 346.526 | -0.000 | 0.000 | 0.000 |
| -62.876 | 62.876 | -0.000 | 59.189 | -0.000 | 0.000 |
| 0.700 | 0.701 | -0.733 | -0.000 | 57.893 | -62.045 |
| 0.000 | -0.000 | -0.000 | -0.000 | -62.876 | 102.153 |
| 314.257 | 114.911 | 72.667 | -62.010 | -0.000 | -0.000 |
| 114.912 | 314.256 | 72.667 | 62.010 | -0.000 | -0.000 |
| 70.447 | 70.447 | 360.619 | -0.000 | -0.000 | -0.000 |
| -62.876 | 62.876 | 0.000 | 59.189 | 0.000 | -0.000 |
| -0.700 | -0.701 | 0.733 | 0.000 | 57.893 | -62.045 |
| -0.000 | 0.000 | 0.000 | 0.000 | -62.876 | 102.153 |
| 318.893 | 113.088 | 69.015 | -61.514 | 0.000 | 0.000 |
| 113.088 | 318.893 | 69.015 | 61.514 | 0.000 | 0.000 |
| -330.529 | -330.529 | 1193.208 | 0.000 | 0.000 | 0.000 |
| -61.514 | 61.514 | 0.000 | 54.897 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 54.897 | -61.514 |
| 0.000 | 0.000 | 0.000 | 0.000 | -61.514 | 102.902 |
| 318.893 | 113.088 | 69.015 | -61.514 | -0.000 | 0.000 |
| 523.792 | 704.415 | -764.162 | 58.338 | -0.000 | 0.000 |
| 467.982 | 467.982 | -493.865 | -0.000 | -0.000 | 0.000 |
| 338.835 | 459.735 | -843.944 | 53.643 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 54.897 | -61.514 |
| 0.000 | -0.000 | -0.000 | -0.000 | -61.514 | 102.902 |
| 266.377 | 85.393 | 157.368 | -58.383 | 0.000 | -0.000 |
| 85.393 | 266.377 | 157.368 | 58.383 | 0.000 | -0.000 |
| 36.136 | 36.136 | 371.217 | 0.000 | 0.000 | -0.000 |
| -98.202 | 18.478 | 83.831 | 53.090 | 0.000 | 0.000 |
| -39.862 | -39.862 | 83.831 | -0.000 | 53.090 | -58.340 |
| -39.930 | -39.931 | 84.430 | -0.000 | -60.606 | 100.168 |
| 318.893 | 113.088 | 69.015 | -61.514 | -0.000 | -0.000 |
| 155.180 | 355.528 | -13.402 | 60.621 | -0.000 | -0.000 |
| 66.805 | 66.805 | 365.600 | -0.000 | -0.000 | 0.000 |
| -61.514 | 61.514 | 0.000 | 54.897 | -0.000 | -0.000 |
| 39.862 | 39.862 | -83.831 | 0.000 | 53.090 | -58.340 |
| 39.930 | 39.931 | -84.430 | 0.000 | -60.606 | 100.168 |
| 311.611 | 111.264 | 79.385 | -60.622 | 0.000 | -0.000 |
| 111.367 | 311.597 | 78.742 | 60.595 | 0.000 | -0.000 |
| 66.804 | 66.804 | 365.601 | 0.000 | 0.000 | 0.000 |
| -62.264 | 54.907 | 7.735 | 53.229 | 0.000 | -0.000 |
| -3.991 | -3.991 | 8.411 | -0.000 | 53.895 | -60.666 |
| 0.000 | -0.000 | -0.000 | -0.000 | -61.514 | 102.902 |
| 319.564 | 119.338 | 61.895 | -60.594 | -0.000 | 0.000 |
| 119.245 | 319.593 | 62.521 | 60.621 | -0.000 | 0.000 |
| 72.720 | 72.720 | 341.236 | -0.000 | -0.000 | 0.000 |
| -54.907 | 62.264 | -7.735 | 53.229 | -0.000 | -0.000 |
| 3.991 | 3.991 | -8.411 | 0.000 | 53.895 | -60.666 |
| -0.000 | 0.000 | 0.000 | 0.000 | -61.514 | 102.902 |
| 25.604 | 28.842 | 28.842 | -0.000 | -0.000 | -0.000 |
| 28.842 | 25.604 | 28.842 | -0.000 | -0.000 | -0.000 |
| 28.842 | 28.842 | 25.604 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 19.381 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 19.381 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 19.381 |
| 25.604 | 28.842 | 28.842 | 0.000 | 0.000 | 0.000 |
| 28.842 | 25.604 | 28.842 | 0.000 | 0.000 | 0.000 |
| 28.842 | 28.842 | 25.604 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 19.381 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 19.381 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 19.381 |
| 25.604 | 28.842 | 28.842 | -0.000 | -0.000 | -0.000 |
| 28.842 | 25.604 | 28.842 | -0.000 | -0.000 | -0.000 |
| 28.842 | 28.842 | 25.604 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 19.381 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.381 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 19.381 |
| 25.604 | 28.842 | 28.842 | 0.000 | 0.000 | 0.000 |
| 28.842 | 25.604 | 28.842 | 0.000 | 0.000 | 0.000 |
| 28.842 | 28.842 | 25.604 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 19.381 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 19.381 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 19.381 |
| 25.604 | 28.842 | 28.842 | -0.000 | -0.000 | -0.000 |
| 28.842 | 25.604 | 28.842 | -0.000 | -0.000 | -0.000 |
| 28.842 | 28.842 | 25.604 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -6.333 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -6.333 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -6.333 |
| 25.604 | 28.842 | 28.842 | 0.000 | 0.000 | 0.000 |
| 28.842 | 25.604 | 28.842 | 0.000 | 0.000 | 0.000 |
| 28.842 | 28.842 | 25.604 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -6.333 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -6.333 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -6.333 |
| 288.712 | 54.031 | 54.031 | -0.000 | 0.000 | 0.000 |
| 54.031 | 288.712 | 54.031 | 0.000 | 0.000 | 0.000 |
| 54.031 | 54.031 | 288.712 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 26.048 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 26.048 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 26.048 |
| 288.712 | 54.031 | 54.031 | 0.000 | -0.000 | -0.000 |
| 54.031 | 288.712 | 54.031 | -0.000 | -0.000 | -0.000 |
| 54.031 | 54.031 | 288.712 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 26.048 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 26.048 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 26.048 |
| 288.712 | 54.031 | 54.031 | -0.000 | 0.000 | 0.000 |
| 54.031 | 288.712 | 54.031 | -0.000 | -0.000 | 0.000 |
| 54.031 | 54.031 | 288.712 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 56.433 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 56.433 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 56.433 |
| 293.995 | 51.390 | 51.390 | -0.000 | -0.000 | -0.000 |
| 51.390 | 293.995 | 51.390 | -0.000 | -0.000 | -0.000 |
| 51.390 | 51.390 | 293.995 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 56.433 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 56.433 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 56.433 |
| 288.710 | 54.027 | 54.027 | 0.000 | 0.000 | 0.000 |
| 54.027 | 288.710 | 54.027 | 0.000 | 0.000 | 0.000 |
| 54.027 | 54.027 | 288.710 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 26.048 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 26.048 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 26.048 |
| 288.713 | 54.035 | 54.035 | -0.000 | -0.000 | -0.000 |
| 54.035 | 288.713 | 54.035 | 0.000 | -0.000 | -0.000 |
| 54.035 | 54.035 | 288.713 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 26.048 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 26.048 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 26.048 |
| 129.515 | 148.696 | 148.696 | 0.000 | 0.000 | -0.000 |
| 148.696 | 129.515 | 148.696 | 0.000 | 0.000 | -0.000 |
| 148.696 | 148.696 | 129.515 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 134.808 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 134.808 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 134.808 |
| 129.515 | 148.696 | 148.696 | -0.000 | -0.000 | 0.000 |
| 148.696 | 129.515 | 148.696 | -0.000 | -0.000 | -0.000 |
| 148.696 | 148.696 | 129.515 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 134.808 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 134.808 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 134.808 |
| 129.515 | 148.696 | 148.696 | 0.000 | 0.000 | -0.000 |
| 148.696 | 129.515 | 148.696 | 0.000 | 0.000 | -0.000 |
| 148.696 | 148.696 | 129.515 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 134.808 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 134.808 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 134.808 |
| 129.516 | 148.696 | 148.696 | -0.000 | -0.000 | 0.000 |
| 148.696 | 129.516 | 148.696 | -0.000 | -0.000 | 0.000 |
| 148.696 | 148.696 | 129.516 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 134.808 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 134.808 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 134.808 |
| 129.513 | 148.696 | 148.696 | 0.000 | 0.000 | -0.000 |
| 148.696 | 129.513 | 148.696 | 0.000 | 0.000 | 0.000 |
| 148.696 | 148.696 | 129.513 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 134.808 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 134.808 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 134.808 |
| 129.517 | 148.696 | 148.696 | 0.000 | -0.000 | 0.000 |
| 148.696 | 129.517 | 148.696 | 0.000 | -0.000 | 0.000 |
| 148.696 | 148.696 | 129.517 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 134.808 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 134.808 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 134.808 |
| 255.825 | 135.237 | 135.237 | -0.000 | -0.000 | 0.000 |
| 135.237 | 255.825 | 135.237 | -0.000 | 0.000 | 0.000 |
| 135.237 | 135.237 | 255.825 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 124.166 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 124.166 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 124.166 |
| 255.825 | 135.237 | 135.237 | -0.000 | -0.000 | -0.000 |
| 135.237 | 255.825 | 135.237 | -0.000 | -0.000 | -0.000 |
| 135.237 | 135.237 | 255.825 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 124.166 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 124.166 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 124.166 |
| 255.825 | 135.237 | 135.237 | -0.000 | -0.000 | -0.000 |
| 135.237 | 255.825 | 135.237 | 0.000 | -0.000 | -0.000 |
| 135.237 | 135.237 | 255.825 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 124.166 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 124.166 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 124.166 |
| 255.825 | 135.237 | 135.237 | -0.000 | 0.000 | -0.000 |
| 135.237 | 255.825 | 135.237 | -0.000 | -0.000 | -0.000 |
| 135.237 | 135.237 | 255.825 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 124.166 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 124.166 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 124.166 |
| 255.826 | 135.238 | 135.238 | -0.000 | -0.000 | 0.000 |
| 135.238 | 255.826 | 135.238 | 0.000 | -0.000 | 0.000 |
| 135.238 | 135.238 | 255.826 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 124.166 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 124.166 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 124.166 |
| 255.824 | 135.237 | 135.237 | 0.000 | -0.000 | -0.000 |
| 135.237 | 255.824 | 135.237 | 0.000 | 0.000 | -0.000 |
| 135.237 | 135.237 | 255.824 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 124.166 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 124.166 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 124.166 |
| 312.720 | 118.771 | 92.808 | 0.000 | 0.000 | 0.000 |
| 118.771 | 312.720 | 92.808 | -0.000 | 0.000 | 0.000 |
| 92.191 | 92.191 | 358.476 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 82.108 | 0.000 | 0.000 |
| 0.021 | 0.021 | -0.004 | 0.000 | 81.697 | 0.000 |
| 0.010 | 0.010 | -0.002 | -0.000 | 0.000 | 90.220 |
| 323.365 | 113.944 | 92.266 | 0.000 | -0.000 | -0.000 |
| 126.970 | 307.537 | 92.527 | -0.000 | -0.000 | -0.000 |
| 92.191 | 92.191 | 358.476 | 0.000 | -0.000 | -0.000 |
| -0.021 | -0.020 | 0.004 | 81.697 | -0.000 | -0.000 |
| -0.021 | -0.021 | 0.004 | 0.000 | 81.697 | -0.000 |
| -0.010 | -0.010 | 0.002 | 0.000 | -0.000 | 90.220 |
| 312.739 | 118.743 | 92.809 | 0.000 | 0.000 | 0.000 |
| 118.743 | 312.739 | 92.809 | 0.000 | 0.000 | 0.000 |
| 92.443 | 92.443 | 358.430 | -0.000 | 0.000 | 0.000 |
| 0.002 | 0.002 | -0.000 | 81.697 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 82.108 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 104.711 |
| 307.543 | 126.976 | 92.526 | -0.000 | -0.000 | -0.000 |
| 113.944 | 323.365 | 92.266 | 0.000 | -0.000 | -0.000 |
| 92.442 | 92.442 | 358.430 | -0.000 | -0.000 | -0.000 |
| -0.002 | -0.002 | 0.000 | 81.697 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 82.108 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 104.711 |
| 312.742 | 118.740 | 92.809 | 0.000 | 0.000 | 0.000 |
| 118.741 | 312.742 | 92.809 | 0.000 | 0.000 | 0.000 |
| 92.191 | 92.191 | 358.478 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 81.697 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 82.108 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 104.711 |
| 323.363 | 113.943 | 92.266 | 0.000 | -0.000 | -0.000 |
| 118.739 | 312.739 | 92.809 | 0.000 | -0.000 | -0.000 |
| 92.442 | 92.442 | 358.428 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 81.697 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 82.108 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 104.711 |
| 260.890 | 134.167 | 136.948 | -0.000 | -0.000 | -0.000 |
| 134.167 | 260.890 | 136.948 | -0.000 | -0.000 | -0.000 |
| 136.948 | 136.948 | 243.916 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 127.204 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 127.204 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 124.173 |
| 260.890 | 134.167 | 136.948 | -0.000 | -0.000 | 0.000 |
| 134.167 | 260.890 | 136.948 | -0.000 | -0.000 | 0.000 |
| 136.948 | 136.948 | 243.916 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 127.204 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 127.204 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 124.173 |
| 261.391 | 133.666 | 136.948 | -0.000 | -0.000 | -0.000 |
| 133.666 | 261.391 | 136.948 | -0.000 | 0.000 | -0.000 |
| 136.948 | 136.948 | 243.916 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 127.204 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 127.204 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 124.173 |
| 260.890 | 134.167 | 136.948 | 0.000 | 0.000 | 0.000 |
| 134.167 | 260.890 | 136.948 | -0.000 | -0.000 | 0.000 |
| 136.948 | 136.948 | 243.916 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 127.204 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 127.204 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 124.173 |
| 260.891 | 134.168 | 136.949 | -0.000 | 0.000 | -0.000 |
| 134.168 | 260.891 | 136.949 | 0.000 | -0.000 | -0.000 |
| 136.949 | 136.949 | 243.917 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.001 | 126.863 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.001 | 0.000 | 126.863 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 124.173 |
| 260.889 | 134.166 | 136.947 | 0.000 | 0.000 | 0.000 |
| 134.166 | 260.889 | 136.947 | 0.000 | 0.000 | 0.000 |
| 136.947 | 136.947 | 243.915 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.001 | 126.863 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.001 | 0.000 | 126.863 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 124.173 |
| 324.008 | 114.177 | 92.166 | -0.000 | 0.000 | -0.000 |
| 368.842 | 571.547 | 45.052 | 0.000 | 0.000 | -0.000 |
| 92.166 | 92.166 | 358.534 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 82.128 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 82.128 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 104.915 |
| 324.008 | 114.177 | 92.166 | -0.000 | -0.000 | 0.000 |
| -125.176 | 55.820 | 139.780 | -0.000 | -0.000 | 0.000 |
| 92.166 | 92.166 | 358.534 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 82.128 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 82.128 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 104.915 |
| 344.473 | 141.811 | 87.653 | 0.000 | 0.000 | -0.000 |
| 152.499 | 333.495 | 87.680 | 0.000 | 0.000 | -0.000 |
| 92.166 | 92.166 | 358.534 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 82.128 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 82.128 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 104.915 |
| 293.710 | 91.040 | 97.178 | -0.000 | -0.000 | 0.000 |
| 114.177 | 324.008 | 92.166 | -0.000 | 0.000 | 0.000 |
| 92.166 | 92.166 | 358.533 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 82.128 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 82.128 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 104.915 |
| 324.010 | 114.177 | 92.166 | 0.000 | 0.000 | -0.000 |
| 125.282 | 318.442 | 91.646 | 0.000 | 0.000 | -0.000 |
| 92.166 | 92.166 | 358.535 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 82.128 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 82.128 | -0.000 |
| 3.697 | 3.698 | -0.694 | 0.000 | 0.000 | 99.697 |
| 314.954 | 113.808 | 93.049 | -0.000 | -0.000 | 0.000 |
| 114.176 | 324.006 | 92.165 | -0.000 | 0.000 | 0.000 |
| 92.165 | 92.165 | 358.532 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 82.128 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 82.128 | 0.000 |
| -3.697 | -3.698 | 0.694 | -0.000 | -0.000 | 99.697 |
| 306.849 | 126.731 | 92.617 | -0.000 | -0.000 | 0.000 |
| 126.731 | 306.849 | 92.617 | -0.000 | 0.000 | 0.000 |
| 92.472 | 92.472 | 358.332 | -0.000 | 0.000 | 0.000 |
| 0.035 | 0.035 | -0.006 | 81.670 | 0.000 | 0.000 |
| 0.035 | 0.035 | -0.006 | -0.000 | 81.670 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 104.487 |
| 322.668 | 113.694 | 92.361 | 0.000 | -0.000 | -0.000 |
| 118.422 | 312.068 | 92.903 | 0.000 | -0.000 | -0.000 |
| 92.448 | 92.448 | 358.336 | 0.000 | -0.000 | -0.000 |
| -0.035 | -0.035 | 0.006 | 81.670 | -0.000 | -0.000 |
| -0.035 | -0.035 | 0.006 | 0.000 | 81.670 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 104.487 |
| 306.839 | 126.721 | 92.619 | 0.000 | 0.000 | 0.000 |
| 113.694 | 322.669 | 92.361 | 0.000 | 0.000 | 0.000 |
| 92.461 | 92.461 | 358.334 | 0.000 | 0.000 | 0.000 |
| 0.003 | 0.003 | -0.001 | 81.669 | 0.000 | 0.000 |
| 0.003 | 0.003 | -0.001 | -0.000 | 81.669 | 0.000 |
| 0.005 | 0.005 | -0.001 | -0.000 | 0.000 | 90.756 |
| 312.037 | 118.470 | 92.901 | 0.000 | -0.000 | -0.000 |
| 126.718 | 306.836 | 92.620 | -0.000 | -0.000 | -0.000 |
| 92.458 | 92.458 | 358.334 | 0.000 | 0.000 | -0.000 |
| -0.003 | -0.003 | 0.001 | 81.669 | -0.000 | -0.000 |
| -0.003 | -0.003 | 0.001 | 0.000 | 81.669 | -0.000 |
| -0.005 | -0.005 | 0.001 | -0.000 | -0.000 | 90.756 |
| 306.840 | 126.720 | 92.620 | -0.000 | 0.000 | 0.000 |
| 113.694 | 322.670 | 92.361 | 0.000 | 0.000 | 0.000 |
| 92.460 | 92.460 | 358.335 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 81.669 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 81.669 | 0.000 |
| 0.000 | 0.001 | -0.000 | -0.000 | 0.000 | 90.756 |
| 322.667 | 113.693 | 92.361 | -0.000 | -0.000 | -0.000 |
| 118.474 | 312.033 | 92.901 | 0.000 | -0.000 | -0.000 |
| 92.459 | 92.459 | 358.333 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 81.669 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 81.669 | -0.000 |
| -0.000 | -0.001 | 0.000 | 0.000 | -0.000 | 90.756 |
| 193.665 | 196.778 | 196.778 | 0.000 | 0.000 | -0.000 |
| 196.778 | 193.665 | 196.778 | 0.000 | 0.000 | -0.000 |
| 196.778 | 196.778 | 193.665 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -16.169 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -16.169 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -16.169 |
| 193.665 | 196.778 | 196.778 | -0.000 | -0.000 | -0.000 |
| 196.778 | 193.665 | 196.778 | -0.000 | -0.000 | -0.000 |
| 196.778 | 196.778 | 193.665 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -16.169 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -16.169 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -16.169 |
| 193.665 | 196.778 | 196.778 | 0.000 | -0.000 | 0.000 |
| 196.778 | 193.665 | 196.778 | 0.000 | -0.000 | 0.000 |
| 196.778 | 196.778 | 193.665 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -16.169 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -16.169 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -16.169 |
| 193.665 | 196.778 | 196.778 | -0.000 | -0.000 | -0.000 |
| 196.778 | 193.665 | 196.778 | -0.000 | -0.000 | -0.000 |
| 196.778 | 196.778 | 193.665 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -16.169 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -16.169 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -16.169 |
| 193.665 | 196.778 | 196.778 | 0.000 | 0.000 | 0.000 |
| 196.778 | 193.665 | 196.778 | 0.000 | 0.000 | 0.000 |
| 196.778 | 196.778 | 193.665 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -16.169 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -16.169 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -16.169 |
| 193.665 | 196.778 | 196.778 | -0.000 | -0.000 | -0.000 |
| 196.778 | 193.665 | 196.778 | -0.000 | -0.000 | 0.000 |
| 196.778 | 196.778 | 193.665 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -16.169 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -16.169 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -16.169 |
| 185.348 | 203.040 | 203.040 | 0.000 | 0.000 | 0.000 |
| 203.040 | 185.348 | 203.040 | -0.000 | 0.000 | 0.000 |
| 203.040 | 203.040 | 185.348 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 5.285 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 5.285 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 5.285 |
| 185.347 | 203.040 | 203.040 | -0.000 | 0.000 | -0.000 |
| 203.040 | 185.347 | 203.040 | -0.000 | 0.000 | -0.000 |
| 203.040 | 203.040 | 185.347 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 5.285 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 5.285 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 5.285 |
| 185.348 | 203.040 | 203.040 | 0.000 | 0.000 | 0.000 |
| 203.040 | 185.348 | 203.040 | -0.000 | -0.000 | 0.000 |
| 203.040 | 203.040 | 185.348 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 5.285 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 5.285 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 5.285 |
| 185.347 | 203.040 | 203.040 | -0.000 | 0.000 | -0.000 |
| 203.040 | 185.347 | 203.040 | -0.000 | 0.000 | -0.000 |
| 203.040 | 203.040 | 185.347 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 5.285 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 5.285 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 5.285 |
| 185.348 | 203.040 | 203.040 | 0.000 | 0.000 | 0.000 |
| 203.040 | 185.348 | 203.040 | 0.000 | -0.000 | 0.000 |
| 203.040 | 203.040 | 185.348 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 5.285 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 5.285 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 5.285 |
| 185.347 | 203.039 | 203.039 | -0.000 | 0.000 | -0.000 |
| 203.039 | 185.347 | 203.039 | -0.000 | 0.000 | -0.000 |
| 203.039 | 203.039 | 185.347 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 5.285 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 5.285 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 5.285 |
| 222.621 | 218.145 | 218.145 | -0.000 | 0.000 | -0.000 |
| 218.145 | 222.621 | 218.145 | 0.000 | 0.000 | -0.000 |
| 218.145 | 218.145 | 222.621 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 15.167 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 15.167 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 15.167 |
| 222.621 | 218.145 | 218.145 | 0.000 | -0.000 | 0.000 |
| 218.145 | 222.621 | 218.145 | 0.000 | -0.000 | -0.000 |
| 218.145 | 218.145 | 222.621 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 15.167 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 15.167 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 15.167 |
| 222.622 | 218.145 | 218.145 | -0.000 | 0.000 | -0.000 |
| 218.145 | 222.622 | 218.145 | -0.000 | 0.000 | 0.000 |
| 218.145 | 218.145 | 222.622 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 15.167 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 15.167 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 15.167 |
| 222.621 | 218.145 | 218.145 | 0.000 | -0.000 | -0.000 |
| 218.145 | 222.621 | 218.145 | 0.000 | 0.000 | 0.000 |
| 218.145 | 218.145 | 222.621 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 15.167 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 15.167 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 15.167 |
| 222.622 | 218.146 | 218.146 | -0.000 | 0.000 | -0.000 |
| 218.146 | 222.622 | 218.146 | -0.000 | 0.000 | 0.000 |
| 218.146 | 218.146 | 222.622 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 15.167 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 15.167 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 15.167 |
| 222.621 | 218.145 | 218.145 | 0.000 | -0.000 | -0.000 |
| 218.145 | 222.621 | 218.145 | 0.000 | -0.000 | -0.000 |
| 218.145 | 218.145 | 222.621 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 15.167 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 15.167 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 15.167 |
| 179.053 | 201.649 | 206.520 | 0.000 | 0.000 | -0.000 |
| 201.649 | 179.053 | 206.520 | -0.000 | 0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -6.427 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -6.427 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -11.298 |
| 179.053 | 201.649 | 206.520 | 0.000 | -0.000 | -0.000 |
| 201.649 | 179.053 | 206.520 | -0.000 | -0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -6.427 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -6.427 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -11.298 |
| 179.053 | 201.649 | 206.520 | -0.000 | 0.000 | 0.000 |
| 202.712 | 177.990 | 206.520 | -0.000 | 0.000 | 0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -6.427 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -6.427 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -11.298 |
| 177.990 | 202.712 | 206.520 | -0.000 | -0.000 | -0.000 |
| 201.649 | 179.053 | 206.520 | 0.000 | -0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -6.427 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -6.427 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -11.298 |
| 177.990 | 202.712 | 206.520 | -0.000 | 0.000 | 0.000 |
| 201.649 | 179.053 | 206.520 | -0.000 | 0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -6.427 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -6.427 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -11.298 |
| 179.053 | 201.649 | 206.520 | 0.000 | -0.000 | 0.000 |
| 202.712 | 177.990 | 206.520 | 0.000 | -0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -6.427 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -6.427 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -11.298 |
| 164.112 | 210.830 | 212.200 | -0.000 | -0.000 | 0.000 |
| 210.830 | 164.112 | 212.200 | -0.000 | 0.000 | -0.000 |
| 212.200 | 212.200 | 218.671 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -4.282 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -4.282 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -7.635 |
| 179.836 | 195.106 | 212.200 | -0.000 | -0.000 | 0.000 |
| 210.830 | 164.112 | 212.200 | 0.000 | -0.000 | 0.000 |
| 212.200 | 212.200 | 218.671 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -4.282 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -4.282 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -7.635 |
| 164.112 | 210.830 | 212.200 | -0.000 | -0.000 | -0.000 |
| 210.830 | 164.112 | 212.200 | -0.000 | -0.000 | 0.000 |
| 212.200 | 212.200 | 218.671 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -4.282 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -4.282 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -23.359 |
| 179.836 | 195.106 | 212.200 | 0.000 | 0.000 | 0.000 |
| 195.106 | 179.836 | 212.200 | -0.000 | 0.000 | -0.000 |
| 212.200 | 212.200 | 218.671 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -4.282 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -4.282 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -23.359 |
| 179.836 | 195.106 | 212.200 | 0.000 | -0.000 | 0.000 |
| 195.106 | 179.836 | 212.200 | 0.000 | -0.000 | 0.000 |
| 212.200 | 212.200 | 218.671 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -4.282 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -4.282 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -41.941 |
| 179.836 | 195.106 | 212.199 | 0.000 | 0.000 | -0.000 |
| 272.732 | 102.209 | 212.200 | 0.000 | 0.000 | -0.000 |
| 212.199 | 212.199 | 218.671 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -4.282 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -4.282 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -41.941 |
| 176.927 | 203.775 | 206.520 | -0.000 | 0.000 | -0.000 |
| 201.649 | 179.053 | 206.520 | -0.000 | 0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -6.427 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -6.427 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -13.424 |
| 176.927 | 203.775 | 206.520 | 0.000 | -0.000 | 0.000 |
| 201.649 | 179.053 | 206.520 | 0.000 | -0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -6.427 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -6.427 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -13.424 |
| 179.053 | 201.649 | 206.520 | 0.000 | 0.000 | -0.000 |
| 203.775 | 176.927 | 206.520 | -0.000 | 0.000 | 0.000 |
| 206.520 | 206.520 | 174.182 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -6.427 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -6.427 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -13.424 |
| 179.053 | 201.649 | 206.520 | -0.000 | -0.000 | 0.000 |
| 201.649 | 179.053 | 206.520 | 0.000 | -0.000 | 0.000 |
| 206.520 | 206.520 | 174.182 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -6.427 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -6.427 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -13.424 |
| 179.053 | 201.649 | 206.520 | -0.000 | 0.000 | 0.000 |
| 203.775 | 176.928 | 206.520 | -0.000 | 0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -6.427 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -6.427 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -13.424 |
| 179.053 | 201.649 | 206.520 | -0.000 | -0.000 | -0.000 |
| 203.774 | 176.927 | 206.520 | 0.000 | -0.000 | -0.000 |
| 206.520 | 206.520 | 174.182 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -6.427 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -6.427 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -13.424 |
| 163.004 | 204.897 | 210.033 | 0.000 | 0.000 | -0.000 |
| 194.728 | 173.173 | 210.033 | 0.000 | 0.000 | -0.000 |
| 210.033 | 210.033 | 205.226 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -8.785 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -8.785 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -10.777 |
| 163.004 | 204.897 | 210.033 | -0.000 | -0.000 | 0.000 |
| 204.897 | 163.004 | 210.033 | -0.000 | -0.000 | 0.000 |
| 210.033 | 210.033 | 205.226 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -8.785 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -8.785 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -10.777 |
| 173.174 | 194.728 | 210.033 | 0.000 | 0.000 | -0.000 |
| 204.897 | 163.004 | 210.033 | 0.000 | 0.000 | -0.000 |
| 210.033 | 210.033 | 205.226 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -8.785 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -8.785 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -10.777 |
| 173.173 | 194.728 | 210.033 | -0.000 | -0.000 | 0.000 |
| 194.728 | 173.173 | 210.033 | -0.000 | -0.000 | -0.000 |
| 210.033 | 210.033 | 205.226 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -8.785 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -8.785 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -10.777 |
| 163.005 | 204.897 | 210.033 | 0.000 | 0.000 | -0.000 |
| 219.073 | 148.830 | 210.033 | 0.000 | 0.000 | -0.000 |
| 210.033 | 210.033 | 205.226 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -8.785 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -8.785 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -20.946 |
| 163.004 | 204.897 | 210.033 | -0.000 | -0.000 | 0.000 |
| 204.897 | 163.004 | 210.033 | -0.000 | -0.000 | 0.000 |
| 210.033 | 210.033 | 205.226 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -8.785 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -8.785 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -20.946 |
| 0.001 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 339.396 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 339.396 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 339.396 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 339.396 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 339.397 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 339.395 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 218.913 | 150.975 | 150.975 | -0.000 | 0.000 | 0.000 |
| 150.975 | 218.913 | 150.975 | -0.000 | 0.000 | -0.000 |
| 150.975 | 150.975 | 218.913 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -158.718 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -158.718 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -158.718 |
| 218.913 | 150.975 | 150.975 | 0.000 | -0.000 | -0.000 |
| 150.975 | 218.913 | 150.975 | 0.000 | -0.000 | -0.000 |
| 150.975 | 150.975 | 218.913 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -158.718 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -158.718 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -158.718 |
| 218.913 | 150.975 | 150.975 | -0.000 | 0.000 | 0.000 |
| 150.975 | 218.913 | 150.975 | -0.000 | 0.000 | -0.000 |
| 150.975 | 150.975 | 218.913 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -158.718 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -158.718 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -158.718 |
| 218.913 | 150.975 | 150.975 | 0.000 | -0.000 | -0.000 |
| 150.975 | 218.913 | 150.975 | 0.000 | 0.000 | -0.000 |
| 150.975 | 150.975 | 218.913 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -158.718 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -158.718 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -158.718 |
| 218.913 | 150.975 | 150.975 | 0.000 | 0.000 | -0.000 |
| 150.975 | 218.913 | 150.975 | -0.000 | 0.000 | 0.000 |
| 150.975 | 150.975 | 218.913 | -0.000 | 0.000 | 0.000 |
| 0.006 | 0.003 | 0.003 | -235.849 | -0.000 | -0.000 |
| 0.003 | 0.006 | 0.003 | -0.000 | -235.849 | -0.000 |
| 0.003 | 0.003 | 0.006 | -0.000 | -0.000 | -235.849 |
| 218.912 | 150.975 | 150.975 | -0.000 | -0.000 | 0.000 |
| 150.975 | 218.912 | 150.975 | 0.000 | -0.000 | 0.000 |
| 150.975 | 150.975 | 218.912 | 0.000 | 0.000 | -0.000 |
| -0.006 | -0.003 | -0.003 | -235.849 | 0.000 | -0.000 |
| -0.003 | -0.006 | -0.003 | 0.000 | -235.849 | 0.000 |
| -0.003 | -0.003 | -0.006 | 0.000 | 0.000 | -235.849 |
| 160.308 | 211.587 | 216.136 | 0.000 | -0.000 | -0.000 |
| 211.587 | 160.308 | 216.136 | 0.000 | -0.000 | 0.000 |
| 216.136 | 216.136 | 209.577 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -3.567 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -3.567 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -16.830 |
| 160.308 | 211.587 | 216.136 | -0.000 | 0.000 | 0.000 |
| 211.587 | 160.308 | 216.136 | -0.000 | 0.000 | 0.000 |
| 216.136 | 216.136 | 209.577 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -3.567 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -3.567 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -16.830 |
| 160.308 | 211.587 | 216.136 | -0.000 | -0.000 | -0.000 |
| 211.587 | 160.308 | 216.136 | 0.000 | -0.000 | -0.000 |
| 216.136 | 216.136 | 209.577 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -3.567 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -3.567 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -16.830 |
| 157.739 | 214.156 | 216.136 | -0.000 | 0.000 | 0.000 |
| 214.156 | 157.739 | 216.136 | -0.000 | -0.000 | -0.000 |
| 216.136 | 216.136 | 209.577 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -3.567 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -3.567 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -16.830 |
| 157.070 | 214.827 | 216.137 | 0.000 | -0.000 | -0.000 |
| 214.827 | 157.070 | 216.137 | 0.000 | -0.000 | -0.000 |
| 216.136 | 216.136 | 209.577 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -3.567 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -3.567 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -16.830 |
| 160.308 | 211.587 | 216.136 | -0.000 | 0.000 | 0.000 |
| 211.587 | 160.308 | 216.136 | -0.000 | 0.000 | 0.000 |
| 216.136 | 216.136 | 209.577 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -3.567 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -3.567 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -16.830 |
| 0.004 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.004 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 431.133 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 431.132 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.004 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.004 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 431.133 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.004 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.004 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 431.132 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.004 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.004 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 431.134 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.004 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 431.131 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 428.300 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 428.300 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 428.300 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 428.300 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 428.301 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 428.299 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 176.610 | 209.191 | 196.650 | -0.000 | -0.000 | -0.000 |
| 209.191 | 176.610 | 196.650 | -0.000 | 0.000 | 0.000 |
| 196.650 | 196.650 | 205.931 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -16.015 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -16.015 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -4.004 |
| 176.610 | 209.191 | 196.650 | 0.000 | -0.000 | 0.000 |
| 209.191 | 176.610 | 196.650 | 0.000 | -0.000 | 0.000 |
| 196.650 | 196.650 | 205.931 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -16.015 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -16.015 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -4.004 |
| 176.610 | 209.192 | 196.650 | -0.000 | 0.000 | -0.000 |
| 209.192 | 176.610 | 196.650 | -0.000 | 0.000 | 0.000 |
| 196.650 | 196.650 | 205.931 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -16.015 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -16.015 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -4.004 |
| 176.610 | 209.191 | 196.650 | 0.000 | 0.000 | 0.000 |
| 209.191 | 176.610 | 196.650 | 0.000 | -0.000 | 0.000 |
| 196.650 | 196.650 | 205.931 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -16.015 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -16.015 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -4.004 |
| 176.610 | 209.192 | 196.650 | -0.000 | -0.000 | -0.000 |
| 209.192 | 176.610 | 196.650 | -0.000 | 0.000 | 0.000 |
| 196.650 | 196.650 | 205.931 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -16.015 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -16.015 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -4.004 |
| 176.610 | 209.191 | 196.650 | 0.000 | -0.000 | -0.000 |
| 209.191 | 176.610 | 196.650 | -0.000 | -0.000 | 0.000 |
| 196.650 | 196.650 | 205.932 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -16.015 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -16.015 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -4.004 |
| 216.523 | 204.590 | 224.268 | -0.000 | -0.000 | 0.000 |
| 204.590 | 216.523 | 224.268 | -0.000 | -0.000 | 0.000 |
| 224.268 | 224.268 | 231.516 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 21.129 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 21.129 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 1.334 |
| 216.523 | 204.590 | 224.268 | 0.000 | 0.000 | 0.000 |
| 204.590 | 216.523 | 224.268 | -0.000 | 0.000 | -0.000 |
| 224.268 | 224.268 | 231.516 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 21.129 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 21.129 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 1.334 |
| 216.523 | 204.590 | 224.268 | 0.000 | -0.000 | 0.000 |
| 204.590 | 216.523 | 224.268 | -0.000 | 0.000 | 0.000 |
| 224.268 | 224.268 | 231.516 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 21.129 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 21.129 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 1.334 |
| 216.523 | 204.590 | 224.268 | 0.000 | 0.000 | -0.000 |
| 204.590 | 216.523 | 224.268 | 0.000 | -0.000 | -0.000 |
| 224.268 | 224.268 | 231.516 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 21.129 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 21.129 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 1.334 |
| 216.524 | 204.591 | 224.269 | -0.000 | 0.000 | 0.000 |
| 204.591 | 216.524 | 224.269 | 0.000 | 0.000 | 0.000 |
| 224.269 | 224.269 | 231.517 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 21.129 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 21.129 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 1.334 |
| 216.522 | 204.590 | 224.267 | 0.000 | 0.000 | -0.000 |
| 204.590 | 216.522 | 224.267 | 0.000 | 0.000 | -0.000 |
| 224.268 | 224.268 | 231.516 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 21.129 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 21.129 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 1.334 |
| 164.605 | 228.288 | 228.288 | -0.000 | -0.000 | -0.000 |
| 228.288 | 164.605 | 228.288 | -0.000 | -0.000 | -0.000 |
| 228.288 | 228.288 | 164.605 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 20.429 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 20.429 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 20.429 |
| 164.605 | 228.288 | 228.288 | -0.000 | -0.000 | -0.000 |
| 228.288 | 164.605 | 228.288 | -0.000 | -0.000 | -0.000 |
| 228.288 | 228.288 | 164.605 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 20.429 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 20.429 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 20.429 |
| 164.605 | 228.288 | 228.288 | 0.000 | 0.000 | 0.000 |
| 228.288 | 164.605 | 228.288 | 0.000 | 0.000 | 0.000 |
| 228.288 | 228.288 | 164.605 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 20.429 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 20.429 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 20.429 |
| 164.605 | 228.288 | 228.288 | 0.000 | -0.000 | 0.000 |
| 228.288 | 164.605 | 228.288 | 0.000 | 0.000 | 0.000 |
| 228.288 | 228.288 | 164.605 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 20.429 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 20.429 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 20.429 |
| 164.606 | 228.289 | 228.289 | -0.000 | -0.000 | 0.000 |
| 228.289 | 164.606 | 228.289 | -0.000 | -0.000 | 0.000 |
| 228.289 | 228.289 | 164.606 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 20.429 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 20.429 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 20.429 |
| 164.605 | 228.288 | 228.288 | 0.000 | -0.000 | 0.000 |
| 228.288 | 164.605 | 228.288 | -0.000 | 0.000 | 0.000 |
| 228.288 | 228.288 | 164.605 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 20.429 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 20.429 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 20.429 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.002 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.002 | 0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.019 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.019 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.001 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.001 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 424.304 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.001 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 424.304 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.001 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 424.304 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.001 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 424.304 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.001 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 424.305 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.001 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 424.302 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 208.988 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 208.988 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 208.988 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 208.988 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 208.989 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 208.987 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.001 | -0.001 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.001 | -0.001 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.001 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.001 | 0.001 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.001 | -0.001 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.001 | -0.001 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.001 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 32.645 | 0.362 | 14.810 | -0.000 | -0.000 | 0.000 |
| -23.782 | -74.031 | -17.503 | -0.000 | -0.000 | -0.000 |
| 8.578 | -21.442 | 28.756 | -0.000 | 0.000 | 0.000 |
| -6.147 | -19.336 | -4.559 | 0.089 | 0.000 | 0.000 |
| -4.903 | -16.118 | -3.707 | 0.000 | 14.981 | -0.000 |
| -6.118 | -19.263 | -4.540 | 0.000 | -0.000 | 0.369 |
| 51.576 | 60.556 | 28.759 | 0.000 | 0.000 | 0.000 |
| 6.424 | 19.093 | 4.583 | -0.000 | -0.000 | -0.000 |
| 35.870 | 68.435 | 49.621 | 0.000 | -0.000 | -0.000 |
| 6.147 | 19.336 | 4.559 | 0.089 | -0.000 | -0.000 |
| 4.903 | 16.118 | 3.707 | 0.000 | 14.981 | 0.000 |
| 6.118 | 19.263 | 4.540 | -0.000 | -0.000 | 0.369 |
| -21.341 | -15.559 | -11.179 | 0.000 | -0.000 | 0.000 |
| -2.968 | -10.110 | -2.333 | 0.000 | 0.000 | 0.000 |
| -2.249 | -2.939 | -17.774 | -0.000 | -0.000 | -0.000 |
| -4.354 | -13.481 | -3.170 | 0.097 | 0.000 | -0.000 |
| -0.604 | -2.148 | -0.472 | 0.000 | 14.676 | -0.000 |
| -6.233 | -19.911 | -4.580 | 0.000 | 0.000 | 0.405 |
| -20.773 | -0.228 | -9.227 | 0.000 | 0.000 | 0.000 |
| 2.933 | 7.931 | 1.956 | -0.000 | -0.000 | -0.000 |
| -13.589 | 1.505 | -18.350 | 0.000 | 0.000 | 0.000 |
| 4.354 | 13.481 | 3.170 | 0.097 | -0.000 | 0.000 |
| 0.604 | 2.148 | 0.472 | -0.000 | 14.676 | -0.000 |
| 6.233 | 19.911 | 4.580 | -0.000 | -0.000 | 0.405 |
| -1.313 | -5.429 | -1.030 | 0.000 | -0.000 | -0.000 |
| -0.045 | -2.545 | -0.198 | -0.000 | -0.000 | -0.000 |
| 0.397 | 0.007 | 0.014 | -0.000 | -0.000 | -0.000 |
| -0.418 | -1.458 | -0.322 | 0.084 | -0.000 | -0.000 |
| 0.484 | 0.005 | 0.205 | -0.000 | -0.183 | -0.000 |
| 0.716 | 0.008 | 0.304 | -0.000 | -0.000 | -0.179 |
| -0.651 | -0.006 | -0.282 | 0.000 | 0.000 | 0.000 |
| 0.494 | 0.437 | 0.184 | -0.000 | 0.000 | -0.000 |
| 2.413 | 7.006 | 1.576 | 0.000 | 0.000 | -0.000 |
| 0.712 | 2.440 | 0.541 | 0.081 | 0.000 | 0.000 |
| -0.484 | -0.005 | -0.205 | 0.000 | -0.183 | 0.000 |
| -0.716 | -0.008 | -0.304 | 0.000 | 0.000 | -0.179 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.004 | -0.000 | -0.002 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.001 | -0.000 | -0.003 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.004 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 115.972 | 19.994 | 11.604 | -0.000 | 0.000 | -0.000 |
| -3936.893 | 601.496 | 976.387 | -0.001 | 0.000 | 0.000 |
| 12.178 | 36.434 | 53.245 | 0.000 | -0.000 | -0.000 |
| -872.669 | 273.945 | 1580.823 | 18.025 | -0.000 | 0.000 |
| -822.789 | 261.607 | 1502.618 | -0.000 | -4.940 | 0.000 |
| -872.928 | 273.500 | 1581.003 | -0.000 | 0.000 | 7.434 |
| 850.952 | -244.872 | -1547.090 | -0.000 | 0.000 | 0.000 |
| 887.844 | -244.787 | -1557.574 | 0.000 | -0.000 | -0.000 |
| 826.189 | -238.513 | -1446.987 | 0.000 | -0.000 | -0.000 |
| 872.669 | -273.945 | -1580.823 | 18.025 | 0.000 | -0.000 |
| 822.789 | -261.607 | -1502.618 | 0.000 | -4.940 | -0.000 |
| 872.928 | -273.500 | -1581.003 | 0.000 | -0.000 | 7.434 |
| -34.185 | 25.662 | 104.459 | -0.000 | 0.000 | 0.000 |
| -125.016 | 60.482 | 179.475 | 0.000 | -0.000 | -0.000 |
| 12.178 | 36.434 | 53.245 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 33.454 | -0.000 | -0.000 |
| -86.512 | 27.266 | 157.322 | -0.000 | 2.445 | 0.000 |
| -201.556 | 38.955 | 136.921 | 0.000 | -0.000 | 22.025 |
| 116.309 | -10.979 | -143.476 | 0.000 | -0.000 | -0.000 |
| 103.557 | 0.854 | -137.016 | 0.000 | -0.000 | 0.000 |
| 101.361 | -6.741 | -128.765 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 33.454 | 0.000 | 0.000 |
| 86.512 | -27.266 | -157.322 | 0.000 | 2.445 | -0.000 |
| 201.556 | -38.955 | -136.921 | -0.000 | 0.000 | 22.025 |
| 33.010 | 21.255 | 17.279 | 0.000 | 0.000 | 0.000 |
| 20.389 | 44.202 | 36.255 | 0.000 | -0.000 | -0.000 |
| 6.003 | 21.847 | 39.514 | -0.000 | 0.000 | 0.000 |
| -7.729 | 2.590 | 14.193 | 16.889 | 0.000 | -0.000 |
| -3.197 | 0.694 | 4.463 | -0.000 | 2.376 | -0.000 |
| -5.579 | 1.062 | 8.727 | -0.000 | -0.000 | 7.907 |
| 37.638 | 12.401 | 0.803 | 0.000 | -0.000 | -0.000 |
| 20.389 | 44.202 | 36.255 | 0.000 | -0.000 | 0.000 |
| 16.025 | 19.387 | 23.150 | 0.000 | 0.000 | -0.000 |
| 7.729 | -2.590 | -14.193 | 16.889 | 0.000 | 0.000 |
| 3.197 | -0.694 | -4.463 | 0.000 | 2.376 | -0.000 |
| 5.579 | -1.062 | -8.727 | 0.000 | 0.000 | 7.907 |
| 31.883 | -5.825 | 3.487 | -0.000 | 0.000 | 0.000 |
| -276.632 | -173.905 | -107.697 | 0.000 | 0.000 | -0.000 |
| -778.167 | -358.978 | -237.600 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 11.334 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 9.730 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 4.475 |
| 50.222 | 4.475 | 9.730 | -0.000 | 0.000 | -0.000 |
| 266.377 | 184.148 | 113.695 | 0.000 | 0.000 | 0.000 |
| 46.279 | -0.937 | 2.690 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 11.334 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 9.730 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 4.475 |
| -18.458 | -3.806 | -4.588 | 0.000 | 0.000 | -0.000 |
| -6.507 | -16.251 | -11.323 | -0.000 | -0.000 | -0.000 |
| 9.417 | 11.124 | 8.532 | 0.000 | -0.000 | 0.000 |
| -0.259 | -0.155 | -0.091 | 11.309 | 0.000 | -0.000 |
| -0.272 | -0.163 | -0.095 | -0.000 | 9.708 | 0.000 |
| -2.676 | -1.607 | -0.945 | 0.000 | 0.000 | 4.362 |
| 50.222 | 4.475 | 9.730 | -0.000 | 0.000 | -0.000 |
| -1.846 | -15.446 | -10.333 | -0.000 | 0.000 | 0.000 |
| 10.227 | 11.639 | 8.843 | 0.000 | 0.000 | 0.000 |
| 0.259 | 0.155 | 0.091 | 11.309 | 0.000 | 0.000 |
| 0.272 | 0.163 | 0.095 | -0.000 | 9.708 | -0.000 |
| 2.676 | 1.607 | 0.945 | 0.000 | 0.000 | 4.362 |
| -6.383 | -4.199 | -2.646 | 0.000 | -0.000 | -0.000 |
| -0.162 | -0.251 | -0.184 | 0.000 | 0.000 | -0.000 |
| -0.295 | -0.295 | -0.229 | -0.000 | 0.000 | -0.000 |
| -0.119 | -0.092 | -0.075 | -0.157 | 0.000 | -0.000 |
| -0.365 | -0.238 | -0.160 | -0.000 | -0.156 | 0.000 |
| -0.916 | -0.567 | -0.356 | 0.000 | -0.000 | -0.147 |
| -0.029 | 0.080 | 0.046 | 0.000 | -0.000 | 0.000 |
| 2.284 | 1.496 | 0.913 | -0.000 | -0.000 | -0.000 |
| 7.440 | 4.712 | 3.010 | 0.000 | 0.000 | -0.000 |
| 0.119 | 0.092 | 0.075 | -0.157 | -0.000 | -0.000 |
| 0.365 | 0.238 | 0.160 | 0.000 | -0.156 | 0.000 |
| 1.228 | 0.756 | 0.470 | 0.000 | -0.000 | -0.143 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.001 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.001 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.011 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.001 | -0.009 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.011 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.009 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 31.488 | 9.260 | 8.552 | -0.000 | 8.287 | -0.000 |
| -163.650 | -458.457 | -131.713 | -0.000 | 24.041 | 0.000 |
| 7.003 | 1.458 | 24.296 | 0.000 | 8.812 | -0.000 |
| -19.461 | -51.975 | -15.341 | 1.467 | 2.445 | -0.757 |
| 7.056 | -0.749 | 8.812 | 0.000 | 7.003 | 0.000 |
| -49.746 | -134.104 | -39.253 | -0.750 | 6.386 | 9.193 |
| -862.836 | 63.082 | -486.115 | -0.000 | -329.530 | 0.001 |
| 9.392 | 23.437 | 1.458 | -0.000 | -0.749 | 0.000 |
| 69.305 | 173.225 | 71.480 | -0.000 | -0.511 | -0.000 |
| 0.000 | 0.000 | -0.000 | 1.458 | -0.000 | -0.749 |
| 26.615 | 50.939 | 24.298 | 0.000 | 4.685 | 0.000 |
| 49.747 | 134.105 | 39.253 | -0.750 | -6.386 | 9.193 |
| -64.783 | -177.403 | -47.557 | 0.000 | 7.567 | -0.000 |
| -3.888 | -21.146 | 2.502 | 0.000 | 2.652 | -0.000 |
| -20.033 | -55.984 | -18.129 | 0.000 | 1.885 | -0.000 |
| -5.288 | -14.342 | -4.141 | 1.413 | 0.702 | -0.728 |
| -0.292 | -17.911 | 2.742 | -0.000 | 6.830 | -0.000 |
| -5.380 | -14.305 | -4.194 | -0.735 | 0.658 | 9.023 |
| -20.937 | -3.388 | -7.981 | -0.000 | -6.424 | 0.000 |
| 11.566 | 38.105 | 9.471 | -0.000 | -2.883 | 0.000 |
| 2.751 | 12.247 | 3.147 | -0.000 | -0.909 | 0.000 |
| 5.288 | 14.342 | 4.141 | 1.413 | -0.702 | -0.728 |
| 38.799 | 104.327 | 29.444 | -0.000 | -4.554 | 0.000 |
| 5.380 | 14.305 | 4.194 | -0.735 | -0.658 | 9.023 |
| -7.916 | -20.551 | -5.640 | 0.000 | 0.716 | -0.000 |
| -5.439 | -14.736 | -4.057 | 0.000 | 0.616 | -0.000 |
| -6.832 | -18.475 | -5.078 | 0.000 | 0.719 | -0.000 |
| -2.618 | -7.705 | -2.006 | -0.166 | 0.448 | 0.085 |
| -0.170 | -0.512 | -0.198 | 0.000 | -0.088 | -0.000 |
| -7.309 | -21.202 | -5.511 | 0.030 | 1.000 | -0.361 |
| -0.393 | 0.071 | -0.252 | -0.000 | -0.164 | 0.000 |
| 3.063 | 8.988 | 2.374 | -0.000 | -0.526 | 0.000 |
| 6.460 | 18.235 | 4.752 | -0.000 | -0.800 | 0.000 |
| 2.618 | 7.705 | 2.006 | -0.166 | -0.448 | 0.085 |
| -0.333 | 0.374 | -0.400 | -0.000 | -0.330 | 0.000 |
| -104.482 | -47.729 | -35.768 | 2.834 | -27.112 | -33.610 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.001 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.001 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.010 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.010 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.001 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.002 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.015 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.016 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.001 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.001 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.012 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.012 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | -0.000 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | -0.000 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.001 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.001 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.001 | 0.001 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.001 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.001 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.001 |
| 0.001 | 0.001 | 0.001 | -0.000 | -0.000 | -0.000 |
| 0.001 | 0.001 | 0.001 | -0.000 | 0.000 | -0.000 |
| 0.001 | 0.001 | -0.002 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.001 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.001 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.001 |
| 0.001 | 0.001 | 0.001 | 0.000 | -0.000 | -0.000 |
| 0.001 | 0.001 | 0.001 | -0.000 | -0.000 | -0.000 |
| 0.001 | 0.001 | 0.003 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.001 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.001 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.001 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | -0.000 |
| 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | -0.000 |
| 0.001 | 0.001 | -0.022 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.001 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.001 |
| 0.001 | 0.001 | 0.001 | -0.000 | -0.000 | 0.000 |
| 0.001 | 0.001 | 0.001 | -0.000 | -0.000 | 0.000 |
| 0.001 | 0.001 | 0.024 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.001 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.001 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.001 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.002 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.023 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.023 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.002 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.002 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.016 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.016 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 455.493 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 455.493 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 455.493 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 455.493 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 455.495 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 455.492 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.002 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.002 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.017 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.017 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.001 | -0.001 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.003 | -0.005 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.001 | 0.001 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.003 | 0.005 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 100.696 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.002 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.018 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.018 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -2583.579 | -2577.351 | -2577.351 | -0.146 | -1.711 | -0.221 |
| -2577.351 | -2583.579 | -2577.351 | -0.146 | -1.711 | -0.221 |
| -2577.351 | -2577.351 | -2583.579 | -0.146 | -1.711 | -0.221 |
| 0.000 | -0.000 | 0.000 | 39.974 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 39.974 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 39.974 |
| 80.866 | 71.145 | 71.145 | -0.000 | 0.000 | -0.000 |
| 71.145 | 80.866 | 71.145 | -0.000 | 0.000 | -0.000 |
| 71.145 | 71.145 | 80.866 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 39.974 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 39.974 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 39.974 |
| -82.510 | -83.329 | -83.329 | 0.062 | 0.975 | 0.107 |
| -83.329 | -82.510 | -83.329 | 0.062 | 0.975 | 0.107 |
| -83.329 | -83.329 | -82.510 | 0.062 | 0.975 | 0.107 |
| 0.000 | -0.000 | 0.000 | 39.974 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 39.974 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 39.974 |
| 325.158 | 282.000 | 282.000 | -0.047 | -0.767 | -0.082 |
| 282.000 | 325.158 | 282.000 | -0.047 | -0.767 | -0.082 |
| 282.000 | 282.000 | 325.158 | -0.047 | -0.767 | -0.082 |
| -0.000 | 0.000 | -0.000 | 39.974 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 39.974 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 39.974 |
| 33.549 | 28.909 | 28.909 | 0.004 | 0.056 | 0.006 |
| 18.089 | 22.831 | 18.089 | 0.005 | 0.080 | 0.008 |
| 18.089 | 18.089 | 22.831 | 0.005 | 0.080 | 0.008 |
| 0.000 | -0.000 | 0.000 | 39.974 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 39.974 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 39.974 |
| 42.447 | 36.752 | 36.752 | -0.007 | -0.116 | -0.013 |
| 36.752 | 42.447 | 36.752 | -0.007 | -0.116 | -0.013 |
| 36.752 | 36.752 | 42.447 | -0.007 | -0.116 | -0.013 |
| -0.000 | 0.000 | -0.000 | 39.974 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 39.974 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 39.974 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 372.222 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 372.222 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 372.223 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 372.222 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 372.224 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 372.221 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.001 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.001 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 489.944 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 489.944 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.001 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 489.944 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 489.944 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.001 | -0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 489.945 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.001 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 489.942 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 327.237 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 327.237 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 327.237 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 327.237 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 327.238 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 327.236 | 0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| 170.280 | 191.370 | 0.000 | 0.000 | 0.000 | -0.000 |
| 191.370 | 170.280 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.003 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -67.823 |
| 170.280 | 191.370 | 0.000 | -0.000 | -0.000 | 0.000 |
| 191.370 | 170.280 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.003 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -67.823 |
| 50757202.810 | 78434113.500 | -37.155 | 0.000 | 0.000 | -0.012 |
| 191.370 | 170.280 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.003 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -10.545 |
| 170.280 | 191.370 | 0.000 | -0.000 | -0.000 | -0.000 |
| 248.647 | 113.002 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.003 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -10.545 |
| 5075864.599 | 7843484.374 | -3.715 | 0.000 | 0.000 | -0.000 |
| 6018392.672 | 6065978.512 | 5726605.895 | -7198.232 | -11094.176 | -19363.330 |
| 0.000 | 0.000 | 0.003 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 6034415.378 | 6071029.879 | 5647682.749 | 752.273 | 4420.845 | 26144.496 |
| -6005202.319 | -6054451.392 | -5764168.613 | 10686.404 | 6162.560 | 614.950 |
| 191.369 | 170.279 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.003 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -6068993.560 | -6081880.257 | -5631635.842 | 1927.752 | 3179.536 | 39457.478 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.001 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.002 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.003 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.022 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.023 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 335.306 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 335.306 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 335.306 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 335.306 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 335.307 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 335.305 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.002 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.002 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.023 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.023 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 0.000 |
| 330.680 | 283.957 | 283.957 | -0.000 | -0.000 | -0.000 |
| 283.957 | 330.680 | 283.957 | -0.000 | -0.000 | -0.000 |
| 283.957 | 283.957 | 330.680 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 32.796 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 32.796 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 32.796 |
| 330.680 | 283.957 | 283.957 | 0.000 | 0.000 | 0.000 |
| 283.957 | 330.680 | 283.957 | 0.000 | 0.000 | 0.000 |
| 283.957 | 283.957 | 330.680 | 0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 32.796 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 32.796 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 32.796 |
| 330.680 | 283.957 | 283.957 | -0.000 | -0.000 | -0.000 |
| 283.957 | 330.680 | 283.957 | -0.000 | -0.000 | 0.000 |
| 283.957 | 283.957 | 330.680 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 47.404 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 47.404 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 47.404 |
| 330.680 | 283.957 | 283.957 | 0.000 | 0.000 | 0.000 |
| 283.957 | 330.680 | 283.957 | 0.000 | 0.000 | 0.000 |
| 283.957 | 283.957 | 330.680 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 47.404 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 47.404 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 47.404 |
| 330.680 | 283.958 | 283.958 | -0.000 | -0.000 | -0.000 |
| 283.958 | 330.680 | 283.958 | -0.000 | -0.000 | -0.000 |
| 283.958 | 283.958 | 330.680 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 32.796 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 32.796 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 32.796 |
| 330.679 | 283.957 | 283.957 | 0.000 | 0.000 | 0.000 |
| 283.957 | 330.679 | 283.957 | 0.000 | 0.000 | 0.000 |
| 283.957 | 283.957 | 330.679 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 32.796 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 32.796 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 32.796 |
| 267.601 | 257.300 | 257.300 | -0.000 | -0.000 | 0.000 |
| 257.300 | 267.601 | 257.300 | 0.000 | 0.000 | 0.000 |
| 257.300 | 257.300 | 267.601 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 4.885 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 4.885 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 4.885 |
| 267.601 | 257.300 | 257.300 | -0.000 | 0.000 | -0.000 |
| 257.300 | 267.601 | 257.300 | -0.000 | 0.000 | 0.000 |
| 257.300 | 257.300 | 267.601 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 4.885 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 4.885 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 4.885 |
| 267.601 | 257.300 | 257.300 | 0.000 | 0.000 | 0.000 |
| 257.300 | 267.601 | 257.300 | -0.000 | -0.000 | 0.000 |
| 257.300 | 257.300 | 267.601 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 4.885 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 4.885 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 4.885 |
| 267.601 | 257.300 | 257.300 | -0.000 | 0.000 | 0.000 |
| 257.300 | 267.601 | 257.300 | -0.000 | 0.000 | 0.000 |
| 257.300 | 257.300 | 267.601 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 4.885 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 4.885 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 4.885 |
| 267.602 | 257.301 | 257.301 | 0.000 | -0.000 | 0.000 |
| 257.301 | 267.602 | 257.301 | 0.000 | 0.000 | 0.000 |
| 257.301 | 257.301 | 267.602 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 4.885 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 4.885 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 4.885 |
| 267.599 | 257.299 | 257.299 | -0.000 | 0.000 | 0.000 |
| 257.299 | 267.599 | 257.299 | -0.000 | 0.000 | -0.000 |
| 257.299 | 257.299 | 267.599 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 4.885 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 4.885 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 4.885 |
| 399.389 | 335.272 | 335.272 | -0.000 | 0.000 | -0.000 |
| 335.272 | 399.389 | 335.272 | 0.000 | 0.000 | -0.000 |
| 335.272 | 335.272 | 399.389 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 54.777 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 54.777 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 54.777 |
| 399.389 | 335.272 | 335.272 | 0.000 | -0.000 | 0.000 |
| 335.272 | 399.389 | 335.272 | -0.000 | -0.000 | 0.000 |
| 335.272 | 335.272 | 399.389 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 54.777 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 54.777 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 54.777 |
| 399.389 | 335.272 | 335.272 | 0.000 | 0.000 | -0.000 |
| 335.272 | 399.389 | 335.272 | -0.000 | 0.000 | -0.000 |
| 335.272 | 335.272 | 399.389 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 54.777 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 54.777 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 54.777 |
| 399.389 | 335.272 | 335.272 | -0.000 | -0.000 | 0.000 |
| 335.272 | 399.389 | 335.272 | -0.000 | -0.000 | 0.000 |
| 335.272 | 335.272 | 399.389 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 54.777 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 54.777 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 54.777 |
| 399.390 | 335.273 | 335.273 | 0.000 | 0.000 | -0.000 |
| 335.273 | 399.390 | 335.273 | 0.000 | -0.000 | -0.000 |
| 335.273 | 335.273 | 399.390 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 56.285 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 56.285 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 56.285 |
| 399.387 | 335.271 | 335.271 | -0.000 | -0.000 | 0.000 |
| 335.271 | 399.387 | 335.271 | -0.000 | -0.000 | 0.000 |
| 335.271 | 335.271 | 399.387 | -0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 56.285 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 56.285 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 56.285 |
| 465.205 | 256.215 | 256.215 | -0.000 | 0.000 | -0.000 |
| 256.215 | 465.205 | 256.215 | -0.000 | 0.000 | -0.000 |
| 256.215 | 256.215 | 465.205 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -2.864 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.864 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -2.864 |
| 465.205 | 256.215 | 256.215 | 0.000 | 0.000 | 0.000 |
| 256.215 | 465.205 | 256.215 | 0.000 | 0.000 | 0.000 |
| 256.215 | 256.215 | 465.205 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -2.864 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.864 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -2.864 |
| 465.206 | 256.215 | 256.215 | -0.000 | 0.000 | -0.000 |
| 256.215 | 465.206 | 256.215 | -0.000 | 0.000 | -0.000 |
| 256.215 | 256.215 | 465.206 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -2.864 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.864 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -2.864 |
| 465.205 | 256.215 | 256.215 | 0.000 | -0.000 | 0.000 |
| 256.215 | 465.205 | 256.215 | 0.000 | 0.000 | 0.000 |
| 256.215 | 256.215 | 465.205 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -2.864 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.864 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -2.864 |
| 465.207 | 256.216 | 256.216 | -0.000 | 0.000 | -0.000 |
| 256.216 | 465.207 | 256.216 | -0.000 | 0.000 | -0.000 |
| 256.216 | 256.216 | 465.207 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -2.864 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.864 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | -2.864 |
| 465.203 | 256.214 | 256.214 | 0.000 | -0.000 | 0.000 |
| 256.214 | 465.203 | 256.214 | 0.000 | -0.000 | 0.000 |
| 256.214 | 256.214 | 465.203 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -2.864 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.864 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -2.864 |
| 238.180 | 183.002 | 183.002 | 0.000 | 0.000 | 0.000 |
| 183.002 | 238.180 | 183.002 | 0.000 | 0.000 | 0.000 |
| 183.002 | 183.002 | 238.180 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.920 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.920 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.920 |
| 238.180 | 183.002 | 183.002 | -0.000 | -0.000 | -0.000 |
| 183.002 | 238.180 | 183.002 | -0.000 | -0.000 | -0.000 |
| 183.002 | 183.002 | 238.180 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.920 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.920 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.920 |
| 238.180 | 183.002 | 183.002 | 0.000 | 0.000 | 0.000 |
| 183.002 | 238.180 | 183.002 | 0.000 | 0.000 | 0.000 |
| 183.002 | 183.002 | 238.180 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.920 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.920 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -0.920 |
| 238.180 | 183.002 | 183.002 | -0.000 | -0.000 | 0.000 |
| 183.002 | 238.180 | 183.002 | -0.000 | -0.000 | 0.000 |
| 183.002 | 183.002 | 238.180 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.920 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.920 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -0.920 |
| 238.182 | 183.003 | 183.003 | 0.000 | -0.000 | 0.000 |
| 183.003 | 238.182 | 183.003 | 0.000 | 0.000 | 0.000 |
| 183.003 | 183.003 | 238.182 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.001 | 0.001 | -0.920 | 0.000 | -0.000 |
| 0.001 | 0.000 | 0.001 | 0.000 | -0.920 | 0.000 |
| 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | -0.920 |
| 238.178 | 183.002 | 183.002 | -0.000 | -0.000 | -0.000 |
| 183.002 | 238.178 | 183.002 | -0.000 | -0.000 | -0.000 |
| 183.002 | 183.002 | 238.178 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.001 | -0.001 | -0.920 | -0.000 | -0.000 |
| -0.001 | -0.000 | -0.001 | -0.000 | -0.920 | -0.000 |
| -0.001 | -0.001 | -0.000 | -0.000 | -0.000 | -0.920 |
| 478.095 | 151.396 | 151.396 | 0.000 | 0.000 | 0.000 |
| 151.396 | 478.095 | 151.396 | 0.000 | 0.000 | -0.000 |
| 151.396 | 151.396 | 478.095 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -3.138 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -3.138 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -3.138 |
| 478.095 | 151.396 | 151.396 | -0.000 | 0.000 | 0.000 |
| 151.396 | 478.095 | 151.396 | -0.000 | -0.000 | 0.000 |
| 151.396 | 151.396 | 478.095 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -3.138 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -3.138 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -3.138 |
| 478.095 | 151.396 | 151.396 | 0.000 | -0.000 | -0.000 |
| 151.396 | 478.095 | 151.396 | -0.000 | 0.000 | -0.000 |
| 151.396 | 151.396 | 478.095 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -3.138 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -3.138 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -3.138 |
| 478.095 | 151.396 | 151.396 | -0.000 | -0.000 | -0.000 |
| 151.396 | 478.095 | 151.396 | -0.000 | 0.000 | -0.000 |
| 151.396 | 151.396 | 478.095 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -3.138 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -3.138 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -0.000 | -3.138 |
| 478.096 | 151.396 | 151.396 | 0.000 | -0.000 | -0.000 |
| 151.396 | 478.096 | 151.396 | 0.000 | -0.000 | -0.000 |
| 151.396 | 151.396 | 478.096 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -3.138 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -3.138 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -3.138 |
| 478.094 | 151.396 | 151.396 | -0.000 | -0.000 | 0.000 |
| 151.396 | 478.094 | 151.396 | -0.000 | -0.000 | 0.000 |
| 151.396 | 151.396 | 478.094 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -3.138 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -3.138 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -3.138 |
| 244.606 | 228.424 | 228.424 | -0.000 | -0.000 | 0.000 |
| 228.424 | 244.606 | 228.424 | -0.000 | -0.000 | 0.000 |
| 228.424 | 228.424 | 244.606 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 19.075 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 19.075 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 19.075 |
| 244.606 | 228.424 | 228.424 | 0.000 | 0.000 | -0.000 |
| 228.424 | 244.606 | 228.424 | 0.000 | -0.000 | -0.000 |
| 228.424 | 228.424 | 244.606 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 19.075 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 19.075 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 19.075 |
| 244.605 | 228.423 | 228.423 | -0.000 | 0.000 | 0.000 |
| 228.423 | 244.605 | 228.423 | -0.000 | -0.000 | 0.000 |
| 228.423 | 228.423 | 244.605 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 19.075 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 19.075 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 19.075 |
| 244.606 | 228.424 | 228.424 | 0.000 | 0.000 | -0.000 |
| 228.424 | 244.606 | 228.424 | 0.000 | 0.000 | -0.000 |
| 228.424 | 228.424 | 244.606 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 19.075 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 19.075 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 19.075 |
| 244.601 | 228.421 | 228.421 | -0.000 | -0.000 | 0.000 |
| 228.421 | 244.601 | 228.421 | -0.000 | -0.000 | 0.000 |
| 228.421 | 228.421 | 244.601 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.001 | -0.001 | 41.005 | -0.000 | 0.000 |
| -0.001 | -0.000 | -0.001 | -0.000 | 41.005 | 0.000 |
| -0.001 | -0.001 | -0.000 | -0.000 | 0.000 | 41.005 |
| 244.610 | 228.426 | 228.426 | 0.000 | 0.000 | 0.000 |
| 228.426 | 244.610 | 228.426 | 0.000 | -0.000 | -0.000 |
| 228.426 | 228.426 | 244.610 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.001 | 0.001 | 41.005 | 0.000 | -0.000 |
| 0.001 | 0.000 | 0.001 | 0.000 | 41.005 | -0.000 |
| 0.001 | 0.001 | 0.000 | -0.000 | -0.000 | 41.005 |
| 430.258 | 118.714 | 118.714 | -0.000 | -0.000 | 0.000 |
| 118.714 | 430.258 | 118.714 | -0.000 | -0.000 | -0.000 |
| 118.714 | 118.714 | 430.258 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -10.478 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -10.478 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -10.478 |
| 430.258 | 118.714 | 118.714 | 0.000 | 0.000 | -0.000 |
| 118.714 | 430.258 | 118.714 | 0.000 | 0.000 | -0.000 |
| 118.714 | 118.714 | 430.258 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -10.478 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -10.478 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -10.478 |
| 430.258 | 118.714 | 118.714 | -0.000 | -0.000 | 0.000 |
| 118.714 | 430.258 | 118.714 | 0.000 | -0.000 | 0.000 |
| 118.714 | 118.714 | 430.258 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -10.478 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -10.478 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -10.478 |
| 430.258 | 118.714 | 118.714 | -0.000 | 0.000 | -0.000 |
| 118.714 | 430.258 | 118.714 | 0.000 | 0.000 | -0.000 |
| 118.714 | 118.714 | 430.258 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -10.478 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -10.478 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -10.478 |
| 430.258 | 118.713 | 118.713 | -0.000 | -0.000 | 0.000 |
| 118.713 | 430.258 | 118.713 | -0.000 | -0.000 | 0.000 |
| 118.713 | 118.713 | 430.258 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -10.478 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -10.478 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -10.478 |
| 430.258 | 118.714 | 118.714 | 0.000 | 0.000 | -0.000 |
| 118.714 | 430.258 | 118.714 | 0.000 | 0.000 | -0.000 |
| 118.714 | 118.714 | 430.258 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -10.478 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -10.478 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -10.478 |
| -1530.121 | -1616.633 | -633.540 | -4.590 | 0.000 | -0.000 |
| -1621.306 | -1525.455 | -633.542 | 3.013 | 0.000 | -0.000 |
| -1623.256 | -1623.256 | -543.085 | 0.000 | 0.000 | -0.000 |
| -2.733 | 2.733 | 0.000 | 40.650 | 0.000 | -0.000 |
| -1792.457 | -1792.457 | -802.270 | -0.000 | 40.555 | -3.013 |
| -1792.460 | -1792.460 | -802.272 | 0.000 | -3.013 | 47.925 |
| 277.868 | 180.361 | 173.221 | -2.733 | -0.000 | 0.000 |
| 1963.615 | 2059.465 | 971.002 | 3.013 | -0.000 | 0.000 |
| 1961.656 | 1961.656 | 1061.455 | -0.000 | -0.000 | 0.000 |
| -2.733 | 2.733 | 0.000 | 40.650 | -0.000 | 0.000 |
| 1792.457 | 1792.457 | 802.270 | 0.000 | 40.555 | -3.013 |
| 1792.460 | 1792.460 | 802.272 | -0.000 | -3.013 | 47.925 |
| 83.090 | -3.422 | 88.503 | -4.590 | 0.000 | -0.000 |
| 180.361 | 277.868 | 173.221 | 2.733 | 0.000 | -0.000 |
| -10.046 | -10.046 | 178.958 | 0.000 | 0.000 | -0.000 |
| -2.733 | 2.733 | 0.000 | 40.650 | 0.000 | -0.000 |
| -179.250 | -179.250 | -80.229 | -0.000 | 40.555 | -3.013 |
| -179.285 | -179.285 | -80.245 | -0.000 | -3.013 | 47.925 |
| 277.868 | 180.361 | 173.221 | -2.733 | -0.000 | 0.000 |
| 350.442 | 446.292 | 248.976 | 3.013 | -0.000 | 0.000 |
| 348.445 | 348.445 | 339.412 | -0.000 | -0.000 | 0.000 |
| -2.733 | 2.733 | -0.000 | 40.650 | 0.000 | 0.000 |
| 179.250 | 179.250 | 80.229 | 0.000 | 40.555 | -3.013 |
| 179.285 | 179.285 | 80.245 | 0.000 | -3.013 | 47.925 |
| 248.823 | 152.986 | 160.595 | -3.016 | 0.000 | -0.000 |
| 157.900 | 244.413 | 160.708 | 4.590 | 0.000 | -0.000 |
| 173.692 | 173.692 | 261.198 | 0.000 | 0.000 | 0.000 |
| -22.514 | -13.335 | -8.022 | 40.023 | 0.000 | -0.000 |
| -17.969 | -17.969 | -8.042 | -0.000 | 40.555 | -3.014 |
| 0.000 | 0.001 | 0.000 | -0.000 | -2.733 | 48.754 |
| 280.258 | 193.748 | 176.752 | -4.590 | -0.000 | 0.000 |
| 193.747 | 280.258 | 176.752 | 4.590 | -0.000 | 0.000 |
| 173.691 | 173.691 | 261.193 | -0.000 | -0.000 | 0.000 |
| -2.733 | 2.733 | -0.000 | 40.650 | -0.000 | 0.000 |
| 17.969 | 17.969 | 8.042 | 0.000 | 40.555 | -3.014 |
| -0.000 | -0.001 | -0.000 | 0.000 | -2.733 | 48.754 |
| 265.564 | 175.836 | 173.261 | -2.504 | 0.000 | 0.000 |
| 171.321 | 250.250 | 168.718 | 4.431 | 0.000 | -0.000 |
| 173.261 | 173.261 | 267.797 | -0.000 | 0.000 | 0.000 |
| -2.504 | 2.504 | 0.000 | 40.488 | -0.000 | -0.000 |
| -0.012 | -0.012 | -0.006 | -0.000 | 39.801 | -4.431 |
| -0.012 | -0.012 | -0.006 | 0.000 | -4.431 | 39.465 |
| 265.564 | 175.836 | 173.261 | -2.504 | -0.000 | 0.000 |
| 166.108 | 254.119 | 168.410 | 2.810 | -0.000 | 0.000 |
| 173.261 | 173.261 | 267.797 | -0.000 | -0.000 | -0.000 |
| -4.418 | 4.443 | 0.006 | 39.801 | -0.000 | 0.000 |
| 0.012 | 0.012 | 0.006 | 0.000 | 39.801 | -4.431 |
| 0.012 | 0.012 | 0.006 | 0.000 | -4.431 | 39.465 |
| 265.564 | 175.836 | 173.261 | -2.504 | 0.000 | -0.000 |
| 175.836 | 265.564 | 173.261 | 2.504 | 0.000 | -0.000 |
| 168.718 | 168.718 | 265.716 | 0.000 | 0.000 | -0.000 |
| -4.432 | 4.429 | -0.001 | 39.801 | 0.000 | -0.000 |
| -0.001 | -0.001 | -0.001 | -0.000 | 39.801 | -4.431 |
| 0.000 | 0.000 | 0.000 | -0.000 | -2.504 | 44.864 |
| 265.564 | 175.836 | 173.260 | -2.504 | -0.000 | 0.000 |
| 175.836 | 265.564 | 173.260 | 2.504 | -0.000 | -0.000 |
| 168.719 | 168.719 | 265.716 | 0.000 | -0.000 | -0.000 |
| -2.504 | 2.504 | -0.000 | 40.488 | -0.000 | 0.000 |
| 0.001 | 0.001 | 0.001 | 0.000 | 39.801 | -4.431 |
| -0.000 | -0.000 | -0.000 | 0.000 | -2.504 | 44.864 |
| 250.255 | 171.323 | 168.719 | -4.431 | 0.000 | -0.000 |
| 175.837 | 265.567 | 173.261 | 2.504 | 0.000 | -0.000 |
| 168.719 | 168.719 | 265.719 | -0.000 | 0.000 | -0.000 |
| -2.504 | 2.504 | 0.000 | 40.488 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 40.488 | -2.504 |
| 0.000 | 0.001 | 0.000 | -0.000 | -2.504 | 44.864 |
| 265.562 | 175.836 | 173.260 | -2.504 | -0.000 | 0.000 |
| 175.836 | 265.562 | 173.260 | 2.504 | -0.000 | 0.000 |
| 173.260 | 173.260 | 267.795 | 0.000 | -0.000 | -0.000 |
| -2.504 | 2.504 | -0.000 | 40.488 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 40.488 | -2.504 |
| -0.000 | -0.001 | -0.000 | 0.000 | -2.504 | 44.864 |
| 298.191 | 185.335 | 167.253 | -15.245 | -0.000 | -0.000 |
| 643.292 | 756.139 | 364.634 | 15.228 | -0.000 | -0.000 |
| 631.769 | 631.769 | 543.877 | 0.000 | -0.000 | -0.000 |
| 453.127 | 483.583 | 201.864 | 38.614 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 38.685 | -15.245 |
| 468.354 | 468.354 | 201.863 | 0.000 | -15.228 | 56.424 |
| -180.569 | -293.416 | -39.093 | -15.228 | 0.000 | -0.000 |
| -293.416 | -180.569 | -39.093 | 15.228 | 0.000 | -0.000 |
| 167.898 | 167.898 | 343.946 | -0.000 | 0.000 | 0.000 |
| -483.583 | -453.127 | -201.864 | 38.614 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 38.685 | -15.245 |
| -468.354 | -468.354 | -201.863 | -0.000 | -15.228 | 56.424 |
| 298.191 | 185.335 | 167.253 | -15.245 | -0.000 | -0.000 |
| 185.335 | 298.191 | 167.253 | 15.245 | -0.000 | -0.000 |
| 167.899 | 167.899 | 343.946 | 0.000 | -0.000 | -0.000 |
| 31.710 | 61.961 | 20.186 | 38.187 | -0.000 | -0.000 |
| 46.849 | 46.849 | 20.192 | -0.000 | 38.614 | -15.228 |
| 0.000 | 0.000 | 0.000 | -0.000 | -15.245 | 56.428 |
| 240.949 | 128.102 | 142.584 | -15.228 | 0.000 | 0.000 |
| 128.102 | 240.949 | 142.584 | 15.228 | 0.000 | -0.000 |
| 167.898 | 167.898 | 343.946 | -0.000 | 0.000 | 0.000 |
| -61.961 | -31.710 | -20.186 | 38.187 | 0.000 | 0.000 |
| -46.849 | -46.849 | -20.192 | 0.000 | 38.614 | -15.228 |
| -0.000 | -0.000 | -0.000 | 0.000 | -15.245 | 56.428 |
| 298.193 | 185.335 | 167.254 | -15.245 | -0.000 | -0.000 |
| 179.616 | 292.464 | 164.787 | 15.228 | -0.000 | -0.000 |
| 167.899 | 167.899 | 343.947 | 0.000 | -0.000 | -0.000 |
| -10.410 | 20.046 | 2.077 | 38.612 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 38.685 | -15.245 |
| 4.684 | 4.684 | 2.019 | -0.000 | -15.125 | 56.399 |
| 298.188 | 185.335 | 167.253 | -15.245 | 0.000 | 0.000 |
| 185.334 | 298.188 | 167.253 | 15.245 | 0.000 | 0.000 |
| 167.898 | 167.898 | 343.945 | -0.000 | 0.000 | -0.000 |
| -15.245 | 15.245 | -0.000 | 38.685 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 38.685 | -15.245 |
| -4.684 | -4.684 | -2.019 | 0.000 | -15.125 | 56.399 |
| 276.865 | 170.996 | 162.217 | -14.923 | 0.000 | -0.000 |
| 170.996 | 276.865 | 162.217 | 14.923 | 0.000 | -0.000 |
| 166.800 | 166.800 | 343.368 | 0.000 | -0.000 | -0.000 |
| -14.775 | 14.777 | 0.000 | 37.164 | 0.000 | -0.000 |
| 0.001 | 0.001 | 0.000 | -0.000 | 37.164 | -14.776 |
| 0.001 | 0.001 | 0.000 | -0.000 | -14.776 | 52.890 |
| 287.192 | 181.308 | 166.800 | -14.947 | -0.000 | 0.000 |
| 170.996 | 276.865 | 162.216 | 14.923 | -0.000 | 0.000 |
| 166.800 | 166.800 | 343.368 | -0.000 | -0.000 | 0.000 |
| -14.947 | 14.947 | -0.000 | 37.724 | 0.000 | 0.000 |
| -0.001 | -0.001 | -0.000 | 0.000 | 37.164 | -14.776 |
| -0.001 | -0.001 | -0.000 | 0.000 | -14.776 | 52.890 |
| 276.865 | 170.996 | 162.217 | -14.923 | 0.000 | -0.000 |
| 170.996 | 276.865 | 162.217 | 14.923 | -0.000 | -0.000 |
| 166.800 | 166.800 | 343.368 | 0.000 | 0.000 | -0.000 |
| -14.776 | 14.776 | 0.000 | 37.164 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 37.724 | -14.947 |
| 0.000 | 0.000 | 0.000 | -0.000 | -14.776 | 52.890 |
| 287.191 | 181.308 | 166.800 | -14.947 | -0.000 | 0.000 |
| 170.996 | 276.865 | 162.216 | 14.923 | -0.000 | 0.000 |
| 162.219 | 162.219 | 341.333 | 0.000 | -0.000 | 0.000 |
| -14.947 | 14.947 | -0.000 | 37.724 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 37.724 | -14.947 |
| -0.000 | -0.000 | -0.000 | 0.000 | -14.776 | 52.890 |
| 287.194 | 181.309 | 166.801 | -14.947 | 0.000 | -0.000 |
| 170.997 | 276.867 | 162.217 | 14.923 | -0.000 | -0.000 |
| 166.801 | 166.801 | 343.369 | 0.000 | 0.000 | -0.000 |
| -14.776 | 14.777 | 0.000 | 37.164 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 37.164 | -14.776 |
| 0.000 | 0.001 | 0.000 | -0.000 | -14.776 | 52.890 |
| 287.189 | 181.308 | 166.800 | -14.946 | -0.000 | 0.000 |
| 181.308 | 287.189 | 166.800 | 14.946 | -0.000 | 0.000 |
| 162.219 | 162.219 | 341.332 | -0.000 | 0.000 | 0.000 |
| -14.776 | 14.776 | -0.000 | 37.164 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 37.164 | -14.776 |
| -0.000 | -0.001 | -0.000 | 0.000 | -14.776 | 52.890 |
| 285.960 | 174.276 | 162.789 | 15.187 | -0.000 | -0.000 |
| 184.658 | 296.350 | 167.286 | -15.205 | -0.000 | -0.000 |
| 167.792 | 167.792 | 344.099 | -0.000 | 0.000 | -0.000 |
| 15.078 | -15.083 | -0.001 | 38.070 | 0.000 | -0.000 |
| -0.003 | -0.003 | -0.001 | 0.000 | 38.070 | 15.080 |
| -0.003 | -0.003 | -0.001 | -0.000 | 15.080 | 55.816 |
| 285.961 | 174.277 | 162.789 | 15.187 | -0.000 | 0.000 |
| 174.277 | 285.961 | 162.789 | -15.187 | -0.000 | 0.000 |
| 167.792 | 167.792 | 344.099 | -0.000 | 0.000 | 0.000 |
| 15.083 | -15.078 | 0.001 | 38.070 | -0.000 | 0.000 |
| 0.003 | 0.003 | 0.001 | -0.000 | 38.070 | 15.080 |
| 0.003 | 0.003 | 0.001 | 0.000 | 15.080 | 55.816 |
| 296.351 | 184.658 | 167.286 | 15.205 | -0.000 | -0.000 |
| 184.658 | 296.351 | 167.286 | -15.205 | 0.000 | -0.000 |
| 163.296 | 163.296 | 342.152 | -0.000 | 0.000 | -0.000 |
| 15.205 | -15.205 | 0.000 | 38.578 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 38.070 | 15.080 |
| -0.000 | -0.000 | -0.000 | 0.000 | 15.080 | 55.816 |
| 285.960 | 174.277 | 162.789 | 15.187 | -0.000 | 0.000 |
| 174.277 | 285.960 | 162.789 | -15.187 | 0.000 | 0.000 |
| 167.792 | 167.792 | 344.098 | -0.000 | -0.000 | 0.000 |
| 15.205 | -15.205 | -0.000 | 38.578 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 38.070 | 15.080 |
| 0.000 | 0.000 | 0.000 | -0.000 | 15.080 | 55.816 |
| 285.963 | 174.277 | 162.789 | 15.187 | 0.000 | -0.000 |
| 184.659 | 296.353 | 167.286 | -15.205 | -0.000 | -0.000 |
| 167.792 | 167.792 | 344.100 | -0.000 | 0.000 | -0.000 |
| 15.205 | -15.204 | 0.000 | 38.578 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 38.578 | 15.205 |
| 0.000 | 0.000 | 0.000 | 0.000 | 15.080 | 55.816 |
| 296.348 | 184.658 | 167.286 | 15.205 | 0.000 | 0.000 |
| 174.276 | 285.958 | 162.788 | -15.187 | -0.000 | 0.000 |
| 163.295 | 163.295 | 342.151 | 0.000 | 0.000 | 0.000 |
| 15.080 | -15.080 | -0.000 | 38.070 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 38.578 | 15.205 |
| -0.000 | -0.000 | -0.000 | -0.000 | 15.080 | 55.816 |
| 314.829 | 124.224 | 124.224 | -0.000 | -0.000 | 0.000 |
| 124.224 | 314.829 | 124.224 | -0.000 | 0.000 | 0.000 |
| 124.224 | 124.224 | 314.829 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -72.598 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -72.598 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -72.598 |
| 319.143 | 122.067 | 122.067 | 0.000 | 0.000 | -0.000 |
| 122.067 | 319.143 | 122.067 | 0.000 | 0.000 | -0.000 |
| 122.067 | 122.067 | 319.144 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -72.598 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -72.598 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | -72.598 |
| 319.144 | 122.067 | 122.067 | -0.000 | -0.000 | 0.000 |
| 122.067 | 319.144 | 122.067 | -0.000 | -0.000 | 0.000 |
| 122.067 | 122.067 | 319.144 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -72.598 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | -72.598 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 0.000 | -72.598 |
| 319.143 | 122.067 | 122.067 | 0.000 | -0.000 | -0.000 |
| 122.067 | 319.143 | 122.067 | 0.000 | 0.000 | 0.000 |
| 122.067 | 122.067 | 319.143 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | -72.598 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | -72.598 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | -72.598 |
| 314.830 | 124.224 | 124.224 | -0.000 | -0.000 | 0.000 |
| 124.224 | 314.830 | 124.224 | -0.000 | -0.000 | 0.000 |
| 124.224 | 124.224 | 314.830 | -0.000 | 0.000 | -0.000 |
| 0.001 | -0.000 | -0.000 | -72.598 | 0.000 | 0.000 |
| -0.000 | 0.001 | -0.000 | -0.000 | -72.598 | 0.000 |
| -0.000 | -0.000 | 0.001 | -0.000 | 0.000 | -72.598 |
| 319.143 | 122.067 | 122.067 | 0.000 | -0.000 | -0.000 |
| 122.067 | 319.143 | 122.067 | 0.000 | 0.000 | 0.000 |
| 122.067 | 122.067 | 319.143 | 0.000 | -0.000 | -0.000 |
| -0.001 | 0.000 | 0.000 | -72.598 | -0.000 | -0.000 |
| 0.000 | -0.001 | 0.000 | 0.000 | -72.598 | -0.000 |
| 0.000 | 0.000 | -0.001 | 0.000 | 0.000 | -72.598 |
| 146.819 | 151.010 | 151.010 | -0.000 | 0.000 | 0.000 |
| 151.010 | 146.819 | 151.010 | -0.000 | -0.000 | 0.000 |
| 151.010 | 151.010 | 146.819 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -87.489 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -87.489 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -87.489 |
| 146.819 | 151.010 | 151.010 | 0.000 | -0.000 | -0.000 |
| 151.010 | 146.819 | 151.010 | 0.000 | -0.000 | -0.000 |
| 151.010 | 151.010 | 146.819 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -87.489 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -87.489 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -87.489 |
| 146.819 | 151.010 | 151.010 | 0.000 | -0.000 | 0.000 |
| 151.010 | 146.819 | 151.010 | 0.000 | -0.000 | 0.000 |
| 151.010 | 151.010 | 146.819 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -87.489 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -87.489 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | -87.489 |
| 146.819 | 151.010 | 151.010 | 0.000 | 0.000 | -0.000 |
| 151.010 | 146.819 | 151.010 | -0.000 | -0.000 | -0.000 |
| 151.010 | 151.010 | 146.819 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -87.489 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -87.489 | -0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 0.000 | -87.489 |
| 146.819 | 151.010 | 151.010 | -0.000 | 0.000 | 0.000 |
| 151.010 | 146.819 | 151.010 | 0.000 | 0.000 | 0.000 |
| 151.010 | 151.010 | 146.819 | 0.000 | 0.000 | 0.000 |
| 0.001 | 0.000 | -0.000 | -87.489 | 0.000 | 0.000 |
| 0.000 | 0.001 | -0.000 | -0.000 | -87.489 | 0.000 |
| 0.000 | -0.000 | 0.001 | -0.000 | -0.000 | -87.489 |
| 146.818 | 151.010 | 151.010 | 0.000 | 0.000 | -0.000 |
| 151.010 | 146.818 | 151.010 | 0.000 | 0.000 | -0.000 |
| 151.010 | 151.010 | 146.818 | -0.000 | -0.000 | -0.000 |
| -0.001 | -0.000 | 0.000 | -87.489 | -0.000 | -0.000 |
| -0.000 | -0.001 | 0.000 | 0.000 | -87.489 | -0.000 |
| -0.000 | 0.000 | -0.001 | 0.000 | -0.000 | -87.489 |
| 233.803 | 178.768 | 178.768 | -0.000 | -0.000 | -0.000 |
| 178.768 | 233.803 | 178.768 | -0.000 | -0.000 | -0.000 |
| 178.768 | 178.768 | 233.803 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 81.429 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 81.429 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 81.429 |
| 233.803 | 178.768 | 178.768 | -0.000 | 0.000 | 0.000 |
| 178.768 | 233.803 | 178.768 | -0.000 | -0.000 | -0.000 |
| 178.768 | 178.768 | 233.803 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 81.429 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 81.429 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 81.429 |
| 233.803 | 178.768 | 178.768 | -0.000 | -0.000 | -0.000 |
| 178.768 | 233.803 | 178.768 | -0.000 | -0.000 | -0.000 |
| 178.768 | 178.768 | 233.803 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 81.429 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 81.429 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 81.429 |
| 233.803 | 178.768 | 178.768 | -0.000 | -0.000 | 0.000 |
| 178.768 | 233.803 | 178.768 | -0.000 | -0.000 | 0.000 |
| 178.768 | 178.768 | 233.803 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 81.429 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 81.429 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 81.429 |
| 233.803 | 178.768 | 178.768 | 0.000 | 0.000 | 0.000 |
| 178.768 | 233.803 | 178.768 | 0.000 | 0.000 | 0.000 |
| 178.768 | 178.768 | 233.803 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 81.429 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 81.429 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 81.429 |
| 233.803 | 178.768 | 178.768 | 0.000 | 0.000 | 0.000 |
| 178.768 | 233.803 | 178.768 | 0.000 | 0.000 | 0.000 |
| 178.768 | 178.768 | 233.803 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 81.429 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 81.429 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 81.429 |
| 240.171 | 175.665 | 182.420 | -0.000 | -0.000 | 0.000 |
| 175.665 | 240.171 | 182.420 | -0.000 | 0.000 | -0.000 |
| 182.420 | 182.420 | 244.016 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 50.339 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 50.339 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 79.452 |
| 92.266 | 323.570 | 182.420 | 0.000 | -0.000 | 0.000 |
| 323.570 | 92.266 | 182.420 | 0.000 | -0.000 | -0.000 |
| 182.420 | 182.420 | 244.016 | 0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 50.339 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 50.339 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 79.452 |
| 92.266 | 323.570 | 182.420 | -0.000 | 0.000 | 0.000 |
| 323.570 | 92.266 | 182.420 | -0.000 | -0.000 | 0.000 |
| 182.420 | 182.420 | 244.016 | -0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 50.339 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 50.339 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 79.452 |
| 92.266 | 323.570 | 182.420 | 0.000 | -0.000 | -0.000 |
| 323.570 | 92.266 | 182.420 | 0.000 | 0.000 | 0.000 |
| 182.420 | 182.420 | 244.016 | 0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 50.339 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 50.339 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 79.452 |
| 92.266 | 323.570 | 182.420 | -0.000 | -0.000 | -0.000 |
| 323.570 | 92.266 | 182.420 | -0.000 | 0.000 | 0.000 |
| 182.420 | 182.420 | 244.016 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 50.339 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 50.339 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 79.452 |
| 92.267 | 323.569 | 182.420 | 0.000 | -0.000 | 0.000 |
| 323.569 | 92.267 | 182.420 | 0.000 | -0.000 | -0.000 |
| 182.420 | 182.420 | 244.016 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 50.339 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 50.339 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 79.452 |
| 246.715 | 147.481 | 147.481 | -0.000 | -0.000 | 0.000 |
| 147.481 | 246.715 | 147.481 | -0.000 | -0.000 | 0.000 |
| 147.481 | 147.481 | 246.715 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 124.961 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 124.961 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 124.961 |
| 246.715 | 147.481 | 147.481 | 0.000 | 0.000 | -0.000 |
| 147.481 | 246.715 | 147.481 | 0.000 | 0.000 | -0.000 |
| 147.481 | 147.481 | 246.715 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 124.961 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 124.961 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 124.961 |
| 246.715 | 147.481 | 147.481 | -0.000 | 0.000 | 0.000 |
| 147.481 | 246.715 | 147.481 | -0.000 | 0.000 | 0.000 |
| 147.481 | 147.481 | 246.715 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 124.961 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 124.961 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 124.961 |
| 246.715 | 147.481 | 147.481 | 0.000 | 0.000 | -0.000 |
| 147.481 | 246.715 | 147.481 | 0.000 | -0.000 | -0.000 |
| 147.481 | 147.481 | 246.715 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 124.961 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 124.961 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 124.961 |
| 246.716 | 147.481 | 147.481 | -0.000 | 0.000 | 0.000 |
| 147.481 | 246.716 | 147.481 | -0.000 | 0.000 | 0.000 |
| 147.481 | 147.481 | 246.716 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 124.961 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 124.961 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 124.961 |
| 246.715 | 147.480 | 147.480 | 0.000 | -0.000 | -0.000 |
| 147.480 | 246.715 | 147.480 | -0.000 | 0.000 | -0.000 |
| 147.480 | 147.480 | 246.715 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 124.961 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 124.961 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 124.961 |
| 335.623 | 94.578 | 94.578 | 0.000 | -0.000 | 0.000 |
| 94.578 | 335.623 | 94.578 | 0.000 | -0.000 | -0.000 |
| 94.578 | 94.578 | 335.623 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 44.051 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 59.407 | -0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 59.407 |
| 333.059 | 95.860 | 95.860 | -0.000 | 0.000 | 0.000 |
| 95.860 | 333.059 | 95.860 | -0.000 | 0.000 | 0.000 |
| 95.860 | 95.860 | 333.059 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 44.051 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 59.408 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 59.408 |
| 333.059 | 95.859 | 95.859 | -0.000 | -0.000 | -0.000 |
| 95.859 | 333.059 | 95.859 | 0.000 | -0.000 | -0.000 |
| 95.859 | 95.859 | 333.059 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 44.051 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 44.051 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 44.051 |
| 333.060 | 95.861 | 95.861 | -0.000 | 0.000 | 0.000 |
| 95.861 | 333.060 | 95.861 | -0.000 | 0.000 | 0.000 |
| 95.861 | 95.861 | 333.060 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 44.051 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 44.051 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 44.051 |
| 335.619 | 94.572 | 94.572 | 0.000 | -0.000 | -0.000 |
| 94.572 | 335.619 | 94.572 | 0.000 | 0.000 | -0.000 |
| 94.572 | 94.572 | 335.619 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 59.407 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 59.407 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 59.407 |
| 335.627 | 94.584 | 94.584 | -0.000 | 0.000 | 0.000 |
| 94.584 | 335.627 | 94.584 | -0.000 | 0.000 | 0.000 |
| 94.584 | 94.584 | 335.627 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 59.407 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 59.407 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 59.407 |
| 174.817 | 159.136 | 159.136 | 0.000 | -0.000 | 0.000 |
| 159.136 | 174.817 | 159.136 | 0.000 | -0.000 | 0.000 |
| 159.136 | 159.136 | 174.817 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 112.935 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 112.935 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 112.935 |
| 174.817 | 159.136 | 159.136 | -0.000 | -0.000 | 0.000 |
| 159.136 | 174.817 | 159.136 | -0.000 | 0.000 | 0.000 |
| 159.136 | 159.136 | 174.817 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 112.935 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 112.935 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 0.000 | 112.935 |
| 174.817 | 159.136 | 159.136 | 0.000 | -0.000 | -0.000 |
| 159.136 | 174.817 | 159.136 | 0.000 | -0.000 | -0.000 |
| 159.136 | 159.136 | 174.817 | 0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 112.935 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 112.935 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 112.935 |
| 174.818 | 159.136 | 159.136 | -0.000 | 0.000 | 0.000 |
| 159.136 | 174.818 | 159.136 | -0.000 | 0.000 | 0.000 |
| 159.136 | 159.136 | 174.818 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 112.935 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 112.935 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 112.935 |
| 174.815 | 159.136 | 159.136 | 0.000 | -0.000 | 0.000 |
| 159.136 | 174.815 | 159.136 | 0.000 | -0.000 | 0.000 |
| 159.136 | 159.136 | 174.815 | 0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 112.935 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | -0.000 | 112.935 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -0.000 | 112.935 |
| 174.820 | 159.136 | 159.136 | -0.000 | 0.000 | -0.000 |
| 159.136 | 174.820 | 159.136 | -0.000 | 0.000 | -0.000 |
| 159.136 | 159.136 | 174.820 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 112.935 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 112.935 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | 0.000 | 112.935 |
| 307.594 | 139.730 | 89.781 | 0.000 | -0.000 | 0.000 |
| 139.730 | 307.594 | 89.781 | 0.000 | -0.000 | -0.000 |
| 89.781 | 89.781 | 330.705 | 0.000 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 65.687 | -0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 65.687 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 83.932 |
| 322.962 | 124.362 | 89.781 | -0.000 | 0.000 | 0.000 |
| 124.362 | 322.962 | 89.781 | -0.000 | -0.000 | -0.000 |
| 89.781 | 89.781 | 330.705 | -0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 65.687 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 65.687 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 83.932 |
| 322.962 | 124.361 | 89.781 | 0.000 | 0.000 | -0.000 |
| 124.362 | 322.962 | 89.781 | 0.000 | -0.000 | -0.000 |
| 89.781 | 89.781 | 330.705 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 65.687 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 65.687 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 99.300 |
| 307.594 | 139.730 | 89.781 | -0.000 | -0.000 | 0.000 |
| 124.362 | 322.962 | 89.781 | -0.000 | -0.000 | 0.000 |
| 89.781 | 89.781 | 330.705 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 65.687 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 65.687 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 99.300 |
| 307.595 | 139.730 | 89.781 | 0.000 | 0.000 | 0.000 |
| 139.730 | 307.594 | 89.781 | 0.000 | -0.000 | 0.000 |
| 89.781 | 89.781 | 330.706 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 65.687 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 65.687 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 83.932 |
| 307.592 | 139.730 | 89.782 | -0.000 | 0.000 | -0.000 |
| 139.730 | 307.593 | 89.782 | -0.000 | 0.000 | 0.000 |
| 89.782 | 89.782 | 330.704 | -0.000 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 65.687 | 0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 65.687 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 83.932 |
| 350.738 | 153.449 | 109.889 | 0.000 | -0.000 | -0.000 |
| 167.087 | 337.100 | 109.889 | 0.000 | 0.000 | 0.000 |
| 109.889 | 109.889 | 359.692 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | -0.000 | 58.881 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | 58.881 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 85.007 |
| 350.738 | 153.449 | 109.889 | -0.000 | 0.000 | 0.000 |
| 167.087 | 337.100 | 109.889 | -0.000 | 0.000 | 0.000 |
| 109.889 | 109.889 | 359.692 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 58.881 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 58.881 | -0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 85.007 |
| 337.101 | 167.088 | 109.890 | 0.000 | -0.000 | -0.000 |
| 167.088 | 337.101 | 109.890 | -0.000 | -0.000 | -0.000 |
| 109.890 | 109.890 | 359.693 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 58.881 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 58.881 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 98.644 |
| 337.099 | 167.086 | 109.888 | -0.000 | 0.000 | -0.000 |
| 153.448 | 350.737 | 109.888 | -0.000 | -0.000 | -0.000 |
| 109.888 | 109.888 | 359.691 | 0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 58.881 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 58.881 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 98.644 |
| 337.112 | 167.097 | 109.898 | 0.000 | -0.000 | -0.000 |
| 167.098 | 337.111 | 109.898 | -0.000 | -0.000 | -0.000 |
| 109.898 | 109.898 | 359.701 | 0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | 58.881 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 58.881 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 98.644 |
| 350.726 | 153.439 | 109.879 | -0.000 | 0.000 | 0.000 |
| 167.076 | 337.088 | 109.879 | -0.000 | 0.000 | 0.000 |
| 109.880 | 109.880 | 359.683 | -0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 58.881 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 58.881 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 98.644 |
| 219.434 | 253.020 | 253.020 | -0.000 | 0.000 | 0.000 |
| 253.020 | 219.434 | 253.020 | 0.000 | 0.000 | 0.000 |
| 253.020 | 253.020 | 219.434 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -62.109 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -62.109 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -62.109 |
| 219.434 | 253.020 | 253.020 | -0.000 | -0.000 | -0.000 |
| 253.020 | 219.434 | 253.020 | -0.000 | -0.000 | -0.000 |
| 253.020 | 253.020 | 219.434 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -62.109 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -62.109 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -62.109 |
| 219.434 | 253.020 | 253.020 | 0.000 | 0.000 | 0.000 |
| 253.020 | 219.434 | 253.020 | 0.000 | 0.000 | 0.000 |
| 253.020 | 253.020 | 219.434 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -62.109 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -62.109 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -62.109 |
| 219.434 | 253.020 | 253.020 | -0.000 | -0.000 | -0.000 |
| 253.020 | 219.434 | 253.020 | -0.000 | -0.000 | -0.000 |
| 253.020 | 253.020 | 219.434 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -62.109 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -62.109 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -62.109 |
| 219.434 | 253.021 | 253.021 | 0.000 | 0.000 | 0.000 |
| 253.021 | 219.434 | 253.021 | 0.000 | 0.000 | 0.000 |
| 253.021 | 253.021 | 219.434 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -62.109 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -62.109 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -62.109 |
| 219.433 | 253.019 | 253.019 | -0.000 | -0.000 | -0.000 |
| 253.019 | 219.433 | 253.019 | -0.000 | -0.000 | -0.000 |
| 253.019 | 253.019 | 219.433 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -62.109 | -0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -62.109 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -62.109 |
| -69.821 | 397.498 | 97.949 | -0.000 | -0.000 | -0.000 |
| 397.498 | -69.821 | 97.949 | -0.000 | -0.000 | -0.000 |
| 97.949 | 97.949 | 338.500 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -8.538 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -8.538 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -21.392 |
| 260.886 | 66.791 | 97.949 | -0.000 | -0.000 | 0.000 |
| 66.791 | 260.886 | 97.949 | -0.000 | -0.000 | 0.000 |
| 97.949 | 97.949 | 338.500 | -0.000 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -8.538 | -0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -8.538 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -21.392 |
| -196.627 | 524.305 | 97.949 | 0.000 | 0.000 | -0.000 |
| 524.305 | -196.627 | 97.949 | 0.000 | 0.000 | -0.000 |
| 97.949 | 97.949 | 338.500 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -8.538 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -8.538 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -21.392 |
| 260.886 | 66.791 | 97.949 | 0.000 | -0.000 | 0.000 |
| 66.791 | 260.886 | 97.949 | -0.000 | -0.000 | 0.000 |
| 97.949 | 97.949 | 338.500 | -0.000 | -0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -8.538 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -8.538 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -21.392 |
| -196.632 | 524.307 | 97.949 | 0.000 | 0.000 | -0.000 |
| 524.307 | -196.632 | 97.949 | 0.000 | 0.000 | -0.000 |
| 97.948 | 97.948 | 338.501 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -8.538 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -8.538 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 0.000 | -21.392 |
| -196.622 | 524.302 | 97.948 | -0.000 | -0.000 | 0.000 |
| 524.302 | -196.622 | 97.948 | -0.000 | -0.000 | -0.000 |
| 97.949 | 97.949 | 338.499 | -0.000 | -0.000 | -0.000 |
| 0.000 | -0.000 | 0.000 | -8.538 | -0.000 | -0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -8.538 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -21.392 |
| 188.914 | 140.444 | 233.296 | -44.988 | -0.000 | 0.000 |
| 140.444 | 188.915 | 233.296 | 44.988 | -0.000 | 0.000 |
| 223.741 | 223.741 | 309.297 | 0.000 | -0.000 | 0.000 |
| -44.988 | 44.988 | 0.000 | 75.874 | -0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 75.874 | -44.988 |
| 0.000 | 0.000 | 0.000 | -0.000 | -44.988 | 24.235 |
| 188.915 | 140.444 | 233.296 | -44.988 | 0.000 | -0.000 |
| 140.444 | 188.914 | 233.296 | 44.988 | 0.000 | -0.000 |
| 223.741 | 223.741 | 309.297 | -0.000 | 0.000 | -0.000 |
| -44.987 | 44.988 | -0.000 | 75.874 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 75.874 | -44.988 |
| 0.000 | -0.000 | -0.000 | -0.000 | -44.988 | 24.235 |
| 188.914 | 140.444 | 233.296 | -44.988 | -0.000 | 0.000 |
| 140.444 | 188.915 | 233.296 | 44.988 | -0.000 | 0.000 |
| 223.741 | 223.741 | 309.297 | -0.000 | -0.000 | 0.000 |
| -44.988 | 44.988 | 0.000 | 75.874 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 75.874 | -44.988 |
| 0.000 | 0.000 | 0.000 | -0.000 | -44.988 | 24.235 |
| 188.914 | 140.444 | 233.296 | -44.988 | 0.000 | -0.000 |
| 140.444 | 188.914 | 233.296 | 44.988 | 0.000 | -0.000 |
| 223.741 | 223.741 | 309.297 | 0.000 | 0.000 | -0.000 |
| -44.988 | 44.988 | -0.000 | 75.874 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 75.874 | -44.988 |
| -0.000 | -0.000 | -0.000 | 0.000 | -44.988 | 24.235 |
| 188.915 | 140.444 | 233.297 | -44.988 | -0.000 | 0.000 |
| 140.444 | 188.915 | 233.297 | 44.988 | -0.000 | 0.000 |
| 223.741 | 223.741 | 309.297 | -0.000 | -0.000 | 0.000 |
| -44.988 | 44.988 | 0.000 | 75.874 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 75.874 | -44.988 |
| 0.000 | 0.000 | 0.000 | -0.000 | -44.988 | 24.235 |
| 188.914 | 140.444 | 233.296 | -44.987 | 0.000 | -0.000 |
| 140.444 | 188.914 | 233.296 | 44.987 | 0.000 | -0.000 |
| 223.740 | 223.740 | 309.297 | 0.000 | 0.000 | -0.000 |
| -44.988 | 44.988 | -0.000 | 75.874 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 75.874 | -44.988 |
| -0.000 | -0.000 | -0.000 | 0.000 | -44.988 | 24.235 |
| 383.097 | 86.855 | 86.855 | 0.000 | -0.000 | -0.000 |
| 86.855 | 383.097 | 86.855 | -0.000 | -0.000 | -0.000 |
| 86.855 | 86.855 | 383.097 | 0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -20.086 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -20.086 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -0.000 | -20.086 |
| 383.097 | 86.855 | 86.855 | 0.000 | 0.000 | 0.000 |
| 86.855 | 383.097 | 86.855 | 0.000 | 0.000 | 0.000 |
| 86.855 | 86.855 | 383.097 | 0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | -20.086 | 0.000 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -20.086 | 0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | -20.086 |
| 383.097 | 86.855 | 86.855 | 0.000 | -0.000 | -0.000 |
| 86.855 | 383.097 | 86.855 | -0.000 | -0.000 | -0.000 |
| 86.855 | 86.855 | 383.097 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -20.086 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -20.086 | 0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | -0.000 | -20.086 |
| 383.097 | 86.855 | 86.855 | 0.000 | 0.000 | 0.000 |
| 86.855 | 383.097 | 86.855 | -0.000 | 0.000 | 0.000 |
| 86.855 | 86.855 | 383.097 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -20.086 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -20.086 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | 0.000 | -20.086 |
| 383.097 | 86.855 | 86.855 | 0.000 | -0.000 | -0.000 |
| 86.855 | 383.097 | 86.855 | -0.000 | 0.000 | -0.000 |
| 86.855 | 86.855 | 383.097 | -0.000 | -0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | -20.086 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -20.086 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | -20.086 |
| 383.098 | 86.855 | 86.855 | 0.000 | 0.000 | 0.000 |
| 86.855 | 383.098 | 86.855 | 0.000 | 0.000 | 0.000 |
| 86.855 | 86.855 | 383.098 | 0.000 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -20.086 | 0.000 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -20.086 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | -20.086 |
| 96.695 | 16.549 | 1.602 | -0.000 | -0.000 | -0.000 |
| 18.551 | 35.429 | 1.602 | -0.000 | -0.000 | 0.000 |
| 0.119 | 1.290 | 2.478 | 0.000 | -0.000 | -0.000 |
| 0.386 | 0.461 | 1.691 | -0.872 | -0.000 | 0.000 |
| 414269433.550 | 494208321.142 | 2.323 | 0.001 | 1.772 | -0.000 |
| 0.363 | 0.435 | 1.593 | 0.000 | 0.000 | 18.367 |
| 95.909 | 15.561 | -1.602 | 0.000 | 0.000 | -0.000 |
| 17.765 | 34.440 | -1.602 | 0.000 | 0.000 | -0.000 |
| -0.608 | 0.422 | -0.706 | -0.000 | 0.000 | 0.000 |
| -0.386 | -0.461 | -1.691 | -0.872 | 0.000 | 0.000 |
| -414269433.530 | -494208321.161 | -2.220 | -0.001 | 1.746 | -0.000 |
| -0.363 | -0.435 | -1.593 | -0.000 | 0.000 | 18.367 |
| 96.341 | 16.105 | 0.160 | -0.000 | -0.000 | -0.000 |
| 18.197 | 34.984 | 0.160 | 0.000 | -0.000 | 0.000 |
| -3.305 | -5.398 | 0.160 | 0.000 | -0.000 | -0.000 |
| 0.015 | 0.023 | 0.044 | -1.010 | -0.000 | -0.000 |
| 41426943.859 | 49420832.812 | 0.121 | 0.000 | -0.098 | -0.000 |
| 0.036 | 0.043 | 0.159 | 0.000 | -0.000 | 18.367 |
| 96.262 | 16.006 | -0.160 | -0.000 | 0.000 | 0.000 |
| 18.118 | 34.885 | -0.160 | -0.000 | 0.000 | 0.000 |
| -3.384 | -5.497 | -0.160 | 0.000 | 0.000 | -0.000 |
| -0.015 | -0.023 | -0.044 | -1.010 | 0.000 | 0.000 |
| -41426943.859 | -49420832.812 | -0.121 | -0.000 | -0.098 | 0.000 |
| -0.036 | -0.043 | -0.159 | 0.000 | -0.000 | 18.367 |
| 96.306 | 16.060 | 0.015 | -0.000 | -0.000 | -0.000 |
| 18.162 | 34.939 | 0.015 | 0.000 | -0.000 | -0.000 |
| -3.342 | -5.444 | 0.012 | 0.000 | -0.000 | 0.000 |
| 0.004 | 0.005 | 0.017 | -0.875 | -0.000 | -0.000 |
| 4142694.255 | 4942083.114 | 0.009 | -0.000 | -0.021 | -0.000 |
| 0.004 | 0.004 | 0.016 | 0.000 | -0.000 | 18.367 |
| 96.297 | 16.050 | -0.015 | 0.000 | 0.000 | 0.000 |
| 18.154 | 34.929 | -0.015 | 0.000 | 0.000 | 0.000 |
| -3.348 | -5.451 | -0.012 | -0.000 | 0.000 | -0.000 |
| -0.004 | -0.005 | -0.017 | -0.875 | 0.000 | -0.000 |
| -4142694.256 | -4942083.115 | -0.009 | 0.000 | -0.021 | 0.000 |
| -0.004 | -0.004 | -0.016 | -0.000 | 0.000 | 18.367 |
| 325.761 | 46.268 | 101.959 | -0.000 | 0.000 | -0.000 |
| 46.268 | 325.761 | 101.959 | -0.000 | 0.000 | -0.000 |
| 99.593 | 99.593 | 241.109 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -71.771 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | -71.771 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 7.852 |
| 325.761 | 46.268 | 101.959 | 0.000 | -0.000 | 0.000 |
| 46.268 | 325.761 | 101.959 | 0.000 | -0.000 | 0.000 |
| 99.593 | 99.593 | 241.109 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -71.771 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | -71.771 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 7.852 |
| 325.761 | 46.268 | 101.959 | -0.000 | 0.000 | -0.000 |
| 46.268 | 325.761 | 101.959 | 0.000 | 0.000 | -0.000 |
| 99.593 | 99.593 | 241.109 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -71.771 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -71.771 | -0.000 |
| 0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 7.852 |
| 325.761 | 46.268 | 101.959 | -0.000 | -0.000 | 0.000 |
| 46.268 | 325.761 | 101.959 | -0.000 | -0.000 | 0.000 |
| 99.593 | 99.593 | 241.109 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -71.771 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -71.771 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 7.852 |
| 325.762 | 46.268 | 101.959 | -0.000 | 0.000 | -0.000 |
| 46.268 | 325.762 | 101.959 | -0.000 | 0.000 | -0.000 |
| 99.593 | 99.593 | 241.112 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -71.771 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -71.771 | -0.000 |
| -0.000 | -0.000 | 0.000 | 0.000 | 0.000 | 7.852 |
| 325.760 | 46.268 | 101.960 | 0.000 | -0.000 | 0.000 |
| 46.268 | 325.760 | 101.960 | 0.000 | -0.000 | 0.000 |
| 99.592 | 99.592 | 241.106 | -0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | -71.771 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -71.771 | 0.000 |
| 0.000 | 0.000 | -0.000 | -0.000 | -0.000 | 7.852 |
| 251.523 | 123.831 | 123.831 | 0.000 | -0.000 | -0.000 |
| 123.831 | 251.523 | 123.831 | 0.000 | -0.000 | 0.000 |
| 123.831 | 123.831 | 251.523 | 0.000 | 0.000 | 0.000 |
| -341.587 | -341.587 | -341.587 | 18.054 | 0.000 | -0.000 |
| -341.587 | -341.587 | -341.587 | 0.000 | 18.054 | -0.000 |
| -341.587 | -341.587 | -341.587 | 0.000 | 0.000 | 18.054 |
| 270.284 | 88.868 | 88.868 | -0.000 | 0.000 | 0.000 |
| 88.868 | 270.284 | 88.868 | -0.000 | 0.000 | -0.000 |
| 88.868 | 88.868 | 270.284 | -0.000 | -0.000 | -0.000 |
| 341.587 | 341.587 | 341.587 | 18.054 | 0.000 | -0.000 |
| 341.587 | 341.587 | 341.587 | -0.000 | 18.054 | 0.000 |
| 341.587 | 341.587 | 341.587 | -0.000 | 0.000 | 18.054 |
| 233.841 | 106.423 | 106.423 | 0.000 | -0.000 | -0.000 |
| 106.423 | 233.841 | 106.423 | 0.000 | -0.000 | 0.000 |
| 106.423 | 106.423 | 233.841 | 0.000 | 0.000 | -0.000 |
| -34.973 | -34.973 | -34.973 | 28.249 | 0.000 | 0.000 |
| -34.973 | -34.973 | -34.973 | 0.000 | 28.249 | 0.000 |
| -34.973 | -34.973 | -34.973 | 0.000 | 0.000 | 28.249 |
| 270.283 | 88.868 | 88.868 | -0.000 | -0.000 | -0.000 |
| 88.868 | 270.283 | 88.868 | -0.000 | 0.000 | -0.000 |
| 88.868 | 88.868 | 270.283 | -0.000 | -0.000 | -0.000 |
| 34.973 | 34.973 | 34.973 | 28.249 | 0.000 | 0.000 |
| 34.973 | 34.973 | 34.973 | -0.000 | 28.249 | 0.000 |
| 34.973 | 34.973 | 34.973 | -0.000 | -0.000 | 28.249 |
| 244.717 | 100.980 | 100.980 | 0.000 | -0.000 | -0.000 |
| 100.980 | 244.717 | 100.980 | 0.000 | 0.000 | 0.000 |
| 100.980 | 100.980 | 244.717 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 54.102 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 54.102 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 54.102 |
| 245.645 | 99.209 | 99.209 | -0.000 | -0.000 | 0.000 |
| 99.209 | 245.645 | 99.209 | -0.000 | -0.000 | -0.000 |
| 99.209 | 99.209 | 245.645 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 54.102 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 54.102 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 54.102 |
| 1596.178 | 1444.257 | 1444.257 | -0.000 | 0.000 | 0.000 |
| 1444.257 | 1596.178 | 1444.257 | -0.000 | 0.000 | -0.000 |
| 1444.257 | 1444.257 | 1596.178 | -0.000 | 0.000 | -0.000 |
| 762.533 | 762.533 | 762.533 | 13.496 | 0.000 | 0.000 |
| 762.533 | 762.533 | 762.533 | -0.000 | 13.496 | 0.000 |
| 762.533 | 762.533 | 762.533 | -0.000 | 0.000 | 13.496 |
| 258.717 | 78.437 | 78.437 | 0.000 | -0.000 | -0.000 |
| 78.437 | 258.717 | 78.437 | -0.000 | -0.000 | -0.000 |
| 78.437 | 78.437 | 258.717 | -0.000 | -0.000 | -0.000 |
| -762.533 | -762.533 | -762.533 | 13.496 | -0.000 | -0.000 |
| -762.533 | -762.533 | -762.533 | -0.000 | 13.496 | -0.000 |
| -762.533 | -762.533 | -762.533 | -0.000 | -0.000 | 13.496 |
| 372.613 | 221.269 | 221.269 | -0.000 | 0.000 | 0.000 |
| 221.269 | 372.613 | 221.269 | 0.000 | 0.000 | -0.000 |
| 221.269 | 221.269 | 372.613 | 0.000 | 0.000 | -0.000 |
| 75.734 | 75.734 | 75.734 | 13.771 | 0.000 | 0.000 |
| 75.734 | 75.734 | 75.734 | -0.000 | 13.771 | 0.000 |
| 75.734 | 75.734 | 75.734 | 0.000 | 0.000 | 13.771 |
| 136.702 | 21.911 | 21.911 | 0.000 | -0.000 | -0.000 |
| 21.911 | 136.702 | 21.911 | -0.000 | -0.000 | -0.000 |
| 21.911 | 21.911 | 136.702 | -0.000 | -0.000 | -0.000 |
| -75.734 | -75.734 | -75.734 | 13.771 | -0.000 | -0.000 |
| -75.734 | -75.734 | -75.734 | -0.000 | 13.771 | -0.000 |
| -75.734 | -75.734 | -75.734 | 0.000 | -0.000 | 13.771 |
| 243.600 | 99.377 | 99.377 | 0.000 | 0.000 | 0.000 |
| 99.377 | 243.600 | 99.377 | 0.000 | 0.000 | 0.000 |
| 99.377 | 99.377 | 243.600 | 0.000 | 0.000 | 0.000 |
| 5.234 | 5.234 | 5.234 | 26.127 | 0.000 | -0.000 |
| 5.234 | 5.234 | 5.234 | -0.000 | 26.127 | 0.000 |
| 5.234 | 5.234 | 5.234 | -0.000 | 0.000 | 26.127 |
| 220.802 | 76.781 | 76.781 | -0.000 | -0.000 | -0.000 |
| 76.781 | 220.802 | 76.781 | -0.000 | -0.000 | -0.000 |
| 76.781 | 76.781 | 220.802 | -0.000 | -0.000 | -0.000 |
| -5.234 | -5.234 | -5.234 | 26.127 | -0.000 | -0.000 |
| -5.234 | -5.234 | -5.234 | -0.000 | 26.127 | 0.000 |
| -5.234 | -5.234 | -5.234 | -0.000 | -0.000 | 26.127 |
| -86.378 | -194.249 | -194.249 | 0.000 | -0.000 | 0.000 |
| -194.249 | -86.378 | -194.249 | 0.000 | -0.000 | 0.000 |
| -194.249 | -194.249 | -86.378 | 0.000 | -0.000 | -0.000 |
| -324.098 | -324.098 | -324.098 | 73.484 | -0.000 | 0.000 |
| -324.098 | -324.098 | -324.098 | 0.000 | 73.484 | 0.000 |
| -324.098 | -324.098 | -324.098 | 0.000 | -0.000 | 73.484 |
| 248.317 | 126.308 | 126.308 | 0.000 | -0.000 | 0.000 |
| 126.308 | 248.317 | 126.308 | -0.000 | 0.000 | 0.000 |
| 126.308 | 126.308 | 248.317 | -0.000 | -0.000 | 0.000 |
| 324.098 | 324.098 | 324.098 | 73.484 | 0.000 | -0.000 |
| 324.098 | 324.098 | 324.098 | -0.000 | 73.484 | 0.000 |
| 324.098 | 324.098 | 324.098 | -0.000 | 0.000 | 73.484 |
| 248.317 | 126.308 | 126.308 | -0.000 | 0.000 | -0.000 |
| 126.308 | 248.317 | 126.308 | -0.000 | 0.000 | -0.000 |
| 126.308 | 126.308 | 248.317 | -0.000 | 0.000 | -0.000 |
| -24.639 | -24.639 | -24.639 | 81.031 | -0.000 | -0.000 |
| -24.639 | -24.639 | -24.639 | 0.000 | 81.031 | 0.000 |
| -24.639 | -24.639 | -24.639 | 0.000 | -0.000 | 81.031 |
| 266.527 | 152.739 | 152.739 | -0.000 | 0.000 | -0.000 |
| 152.739 | 266.527 | 152.739 | -0.000 | 0.000 | 0.000 |
| 152.739 | 152.739 | 266.527 | -0.000 | 0.000 | -0.000 |
| 24.639 | 24.639 | 24.639 | 81.031 | 0.000 | 0.000 |
| 24.639 | 24.639 | 24.639 | -0.000 | 81.031 | -0.000 |
| 24.639 | 24.639 | 24.639 | -0.000 | 0.000 | 81.031 |
| 232.552 | 127.775 | 127.775 | 0.000 | -0.000 | 0.000 |
| 127.775 | 232.552 | 127.775 | 0.000 | -0.000 | 0.000 |
| 127.775 | 127.775 | 232.552 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 91.723 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 91.723 | -0.000 |
| 0.000 | 0.000 | 0.000 | -0.000 | 0.000 | 91.723 |
| 244.200 | 130.875 | 130.875 | -0.000 | 0.000 | 0.000 |
| 130.875 | 244.200 | 130.875 | -0.000 | 0.000 | 0.000 |
| 130.875 | 130.875 | 244.200 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 91.723 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | 91.723 | -0.000 |
| -0.000 | -0.000 | -0.000 | 0.000 | -0.000 | 91.723 |
| 241.192 | 128.164 | 128.164 | 0.000 | 0.000 | 0.000 |
| 128.164 | 241.192 | 128.164 | 0.000 | 0.000 | 0.000 |
| 128.164 | 128.164 | 241.192 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 91.641 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | 91.641 | 0.000 |
| -0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 91.641 |
| 241.279 | 128.276 | 128.276 | -0.000 | -0.000 | -0.000 |
| 128.276 | 241.279 | 128.276 | -0.000 | -0.000 | -0.000 |
| 128.276 | 128.276 | 241.279 | -0.000 | -0.000 | -0.000 |
| 0.000 | 0.000 | -0.000 | 91.641 | -0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | 91.641 | 0.000 |
| 0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 91.641 |
| 241.231 | 128.215 | 128.215 | 0.000 | 0.000 | 0.000 |
| 128.215 | 241.231 | 128.215 | 0.000 | 0.000 | 0.000 |
| 128.215 | 128.215 | 241.231 | 0.000 | 0.000 | 0.000 |
| -0.006 | -0.006 | -0.006 | 77.750 | 0.000 | 0.000 |
| -0.006 | -0.006 | -0.006 | 0.000 | 77.750 | 0.000 |
| -0.006 | -0.006 | -0.006 | 0.000 | 0.000 | 77.750 |
| 248.084 | 126.209 | 126.209 | -0.000 | -0.000 | -0.000 |
| 126.209 | 248.084 | 126.209 | 0.000 | -0.000 | -0.000 |
| 126.209 | 126.209 | 248.084 | 0.000 | -0.000 | -0.000 |
| 0.006 | 0.006 | 0.006 | 77.750 | -0.000 | -0.000 |
| 0.006 | 0.006 | 0.006 | -0.000 | 77.750 | -0.000 |
| 0.006 | 0.006 | 0.006 | -0.000 | -0.000 | 77.750 |
| 241.236 | 128.220 | 128.220 | 0.000 | 0.000 | 0.000 |
| 128.220 | 241.236 | 128.220 | 0.000 | 0.000 | 0.000 |
| 128.220 | 128.220 | 241.236 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 91.641 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 91.641 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 91.641 |
| 241.235 | 128.220 | 128.220 | -0.000 | -0.000 | -0.000 |
| 128.220 | 241.235 | 128.220 | -0.000 | -0.000 | -0.000 |
| 128.220 | 128.220 | 241.235 | -0.000 | -0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 91.641 | -0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 91.641 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 91.641 |
| 311.152 | 148.516 | 83.777 | -0.000 | -0.000 | 0.000 |
| 149.036 | 325.463 | 39.926 | -0.000 | -0.000 | 0.000 |
| 87.883 | 40.470 | 312.855 | -0.000 | 0.000 | 0.000 |
| -1273820696.177 | -717988125.428 | -1501853684.245 | 29.836 | -1.825 | -0.114 |
| -0.000 | 0.000 | -0.000 | -0.000 | 29.528 | 0.000 |
| 0.385 | 0.066 | 0.127 | -0.000 | -0.000 | 88.922 |
| 310.381 | 148.384 | 83.524 | 0.000 | -0.000 | 0.000 |
| 148.265 | 325.331 | 39.673 | -0.000 | 0.000 | -0.000 |
| 83.440 | 39.708 | 311.395 | 0.000 | 0.000 | -0.000 |
| 1267083952.215 | 699831815.854 | 1478040727.506 | 4832529.776 | -1638309.554 | -106263.880 |
| -0.000 | -0.000 | 0.000 | 0.000 | 29.528 | -0.000 |
| -0.385 | -0.066 | -0.127 | 0.000 | 0.000 | 88.922 |
| 310.805 | 148.457 | 83.663 | -0.000 | -0.000 | -0.000 |
| 150.768 | 325.760 | 40.495 | -0.000 | -0.000 | 0.000 |
| 83.864 | 39.781 | 311.534 | -0.000 | -0.000 | -0.000 |
| 0.613 | 0.105 | 0.201 | -16.135 | -0.000 | 0.000 |
| 0.290 | 0.050 | 0.095 | -0.000 | -46.313 | 0.000 |
| 0.039 | 0.007 | 0.013 | -0.000 | -0.000 | 88.922 |
| 310.728 | 148.443 | 83.638 | -0.000 | 0.000 | -0.000 |
| 148.612 | 325.390 | 39.787 | 0.000 | 0.000 | -0.000 |
| 83.787 | 39.767 | 311.509 | -0.000 | 0.000 | -0.000 |
| -0.613 | -0.105 | -0.201 | -16.135 | -0.000 | -0.000 |
| -0.290 | -0.050 | -0.095 | 0.000 | -46.313 | -0.000 |
| -0.039 | -0.007 | -0.013 | 0.000 | 0.000 | 88.922 |
| 310.771 | 148.451 | 83.651 | 0.000 | -0.000 | 0.000 |
| 148.655 | 325.399 | 39.800 | -0.000 | -0.000 | 0.000 |
| 83.829 | 39.774 | 311.522 | -0.000 | -0.000 | -0.000 |
| -12484822.411 | -6637004.537 | -14262005.912 | 36082.574 | 7341.436 | 820.539 |
| 0.029 | 0.005 | 0.009 | -0.000 | -46.319 | 0.000 |
| -0.000 | 0.000 | 0.000 | -0.000 | -0.000 | 88.922 |
| 310.761 | 148.449 | 83.649 | 0.000 | 0.000 | -0.000 |
| 148.646 | 325.395 | 39.798 | -0.000 | 0.000 | -0.000 |
| 83.822 | 39.774 | 311.521 | 0.000 | 0.000 | 0.000 |
| 12092318.174 | 6443671.057 | 13218945.811 | 70297.033 | 53082.461 | 2240.620 |
| -0.029 | -0.005 | -0.009 | 0.000 | -46.319 | -0.000 |
| 0.000 | -0.000 | -0.000 | 0.000 | 0.000 | 88.922 |
| 340.794 | 162.788 | 107.212 | 0.000 | -0.000 | -0.000 |
| 163.576 | 332.143 | 108.224 | 0.000 | -0.000 | -0.000 |
| 107.711 | 107.799 | 357.534 | 0.000 | 0.000 | -0.000 |
| -0.000 | 0.000 | -0.000 | 59.204 | 0.000 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | 58.447 | 0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 83.743 |
| 340.794 | 162.788 | 107.212 | -0.000 | 0.000 | -0.000 |
| 163.576 | 332.143 | 108.223 | -0.000 | 0.000 | 0.000 |
| 107.711 | 107.799 | 357.534 | -0.000 | 0.000 | -0.000 |
| 0.000 | -0.000 | -0.000 | 59.203 | 0.000 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 58.447 | 0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 83.743 |
| 340.793 | 162.791 | 107.213 | 0.000 | -0.000 | 0.000 |
| 163.579 | 332.143 | 108.224 | 0.000 | -0.000 | 0.000 |
| 107.645 | 107.866 | 357.534 | 0.000 | 0.000 | -0.000 |
| 0.000 | 0.000 | 0.000 | 59.203 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 58.447 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 83.741 |
| 340.791 | 162.789 | 107.211 | -0.000 | 0.000 | 0.000 |
| 163.577 | 332.140 | 108.223 | -0.000 | 0.000 | -0.000 |
| 107.643 | 107.864 | 357.532 | -0.000 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | 59.203 | 0.000 | 0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 58.447 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | 0.000 | 83.741 |
| 340.804 | 162.800 | 107.222 | 0.000 | -0.000 | 0.000 |
| 163.589 | 332.153 | 108.233 | 0.000 | -0.000 | -0.000 |
| 107.652 | 107.876 | 357.542 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 59.203 | -0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 58.447 | -0.000 |
| -0.000 | 0.000 | -0.000 | 0.000 | -0.000 | 83.741 |
| 340.780 | 162.780 | 107.203 | -0.000 | 0.000 | -0.000 |
| 163.567 | 332.130 | 108.214 | -0.000 | 0.000 | -0.000 |
| 107.634 | 107.857 | 357.524 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | 59.203 | 0.000 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 58.447 | -0.000 |
| 0.000 | -0.000 | 0.000 | -0.000 | -0.000 | 83.741 |
| 290.034 | 195.035 | 98.893 | 0.000 | 0.000 | 0.000 |
| 195.035 | 290.034 | 98.893 | 0.000 | 0.000 | 0.000 |
| 98.892 | 98.893 | 316.922 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -26.267 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -26.267 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 47.499 |
| 154.866 | 330.203 | 98.893 | -0.000 | 0.000 | -0.000 |
| 195.035 | 290.034 | 98.893 | -0.000 | 0.000 | -0.000 |
| 98.892 | 98.892 | 316.922 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -26.267 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -26.267 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | 0.000 | 47.499 |
| 290.034 | 195.035 | 98.893 | 0.000 | 0.000 | 0.000 |
| 330.203 | 154.866 | 98.893 | 0.000 | 0.000 | 0.000 |
| 98.892 | 98.892 | 316.922 | 0.000 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -26.267 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -26.267 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | -0.000 | 47.499 |
| 290.034 | 195.035 | 98.893 | -0.000 | -0.000 | -0.000 |
| 68417801.049 | 58274717.278 | 92243964.248 | -302611.029 | 308829.750 | -639000.505 |
| 98.893 | 98.893 | 316.922 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -26.267 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -26.267 | -0.000 |
| -0.000 | -0.000 | -0.000 | -0.000 | -0.000 | 47.499 |
| 290.035 | 195.035 | 98.893 | 0.000 | -0.000 | 0.000 |
| -6066020.461 | -6312502.753 | -9698196.467 | -56574.861 | 27916.923 | -51543.155 |
| 98.892 | 98.892 | 316.923 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | -26.267 | -0.000 | 0.000 |
| 0.000 | 0.000 | -0.000 | 0.000 | -26.267 | 0.000 |
| -6281951.858 | -6849060.604 | -10383283.990 | -20453.181 | 20876.812 | 10562.632 |
| 5967299.142 | 6514427.542 | 9641686.399 | 6400.829 | 64618.122 | -127823.939 |
| 195.035 | 290.033 | 98.893 | -0.000 | 0.000 | -0.000 |
| 98.893 | 98.893 | 316.921 | -0.000 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -26.267 | 0.000 | -0.000 |
| -0.000 | -0.000 | 0.000 | -0.000 | -26.267 | -0.000 |
| 6303690.601 | 5918407.188 | 9844226.373 | 18301.361 | 8332.636 | 275435.529 |
Phonon and Quasi-Harmonic Approximation Predictions
Phonon band structures and crystal properties estimated from quasi-harmonic approximation (QHA) calculations are displayed for select crystals. The calculations were performed using phonopy and LAMMPS. For the phonon calculations, 3x3 supercells of the potential-specific relaxed crystals were used. The QHA calculations were based on 11 strain states ranging from -0.05 to 0.05.
The calculation method used is available as the iprPy phonon calculation method.
Notes and Disclaimers:
- The thermodynamic properties estimated from QHA are based on the assumption that only volumetric changes affect the phonon behaviors as the temperature changes. This tends to give good predictions at lower temperatures but ignores anharmonic effects such as phonon coupling and vacancy formation that can be important at higher temperatures.
- Note that direct molecular dynamics (MD) simulations using the same potentials will disagree with the thermodynamics properties listed here for the lowest temperatures. The MD results are purely classical in nature and therefore lack a zero-point energy, whereas the phonon calculations inherently provide a zero-point energy.
- The structures explored here are taken from the dynamically relaxed structures above. Despite the rigorous relaxation method used, some of these structures prove to be unstable once internal deformations are added. The phonon results may reflect this and give bad band gap predictions for these unstable crystals.
- All QHA calculations performed here use the same set of strains which might not be ideal for all crystals. Be sure to check the bulk modulus and Helmholtz vs. volume plots to verify if the QHA strained states are reasonable for each crystal of interest.
- QHA results may not be available for all crystal structures that have phonon results. Missing QHA results indicates an issue either with the strained states or with the QHA calculation itself.
- NIST disclaimer
Version Information:
- 2023-03-14. Phonon and QHA plots added
Band Structures, Density of States, and QHA Verification Plots
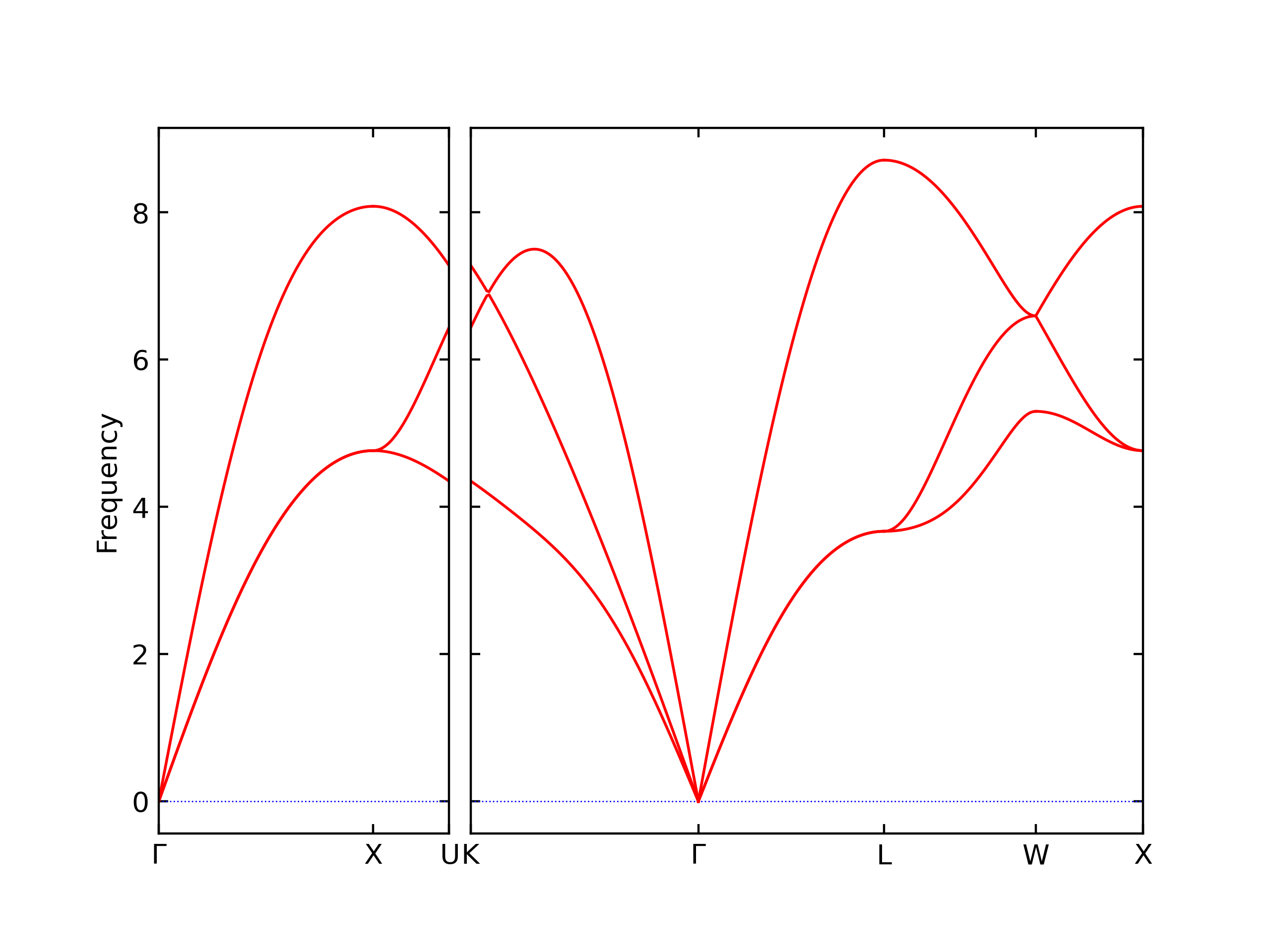
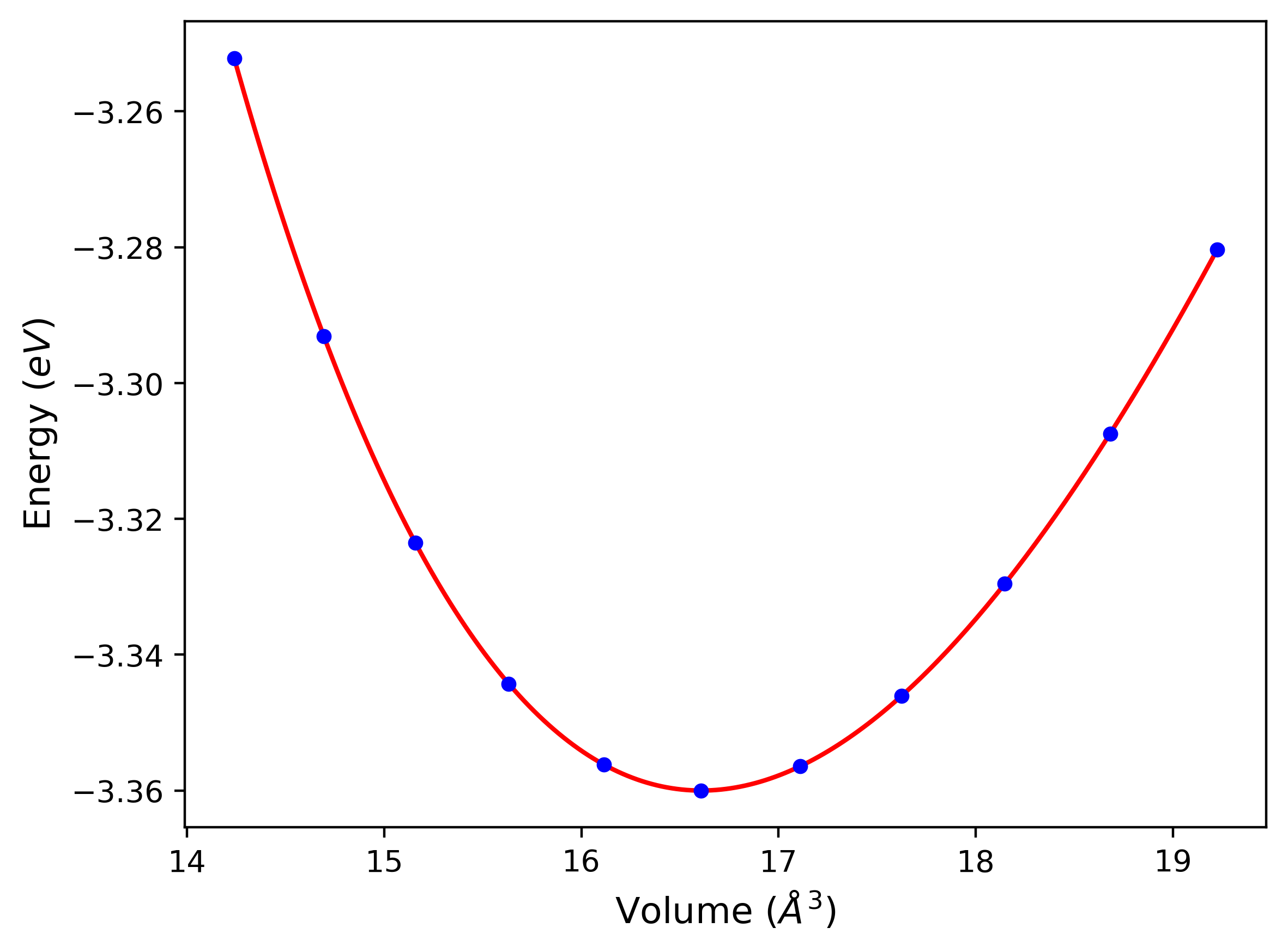
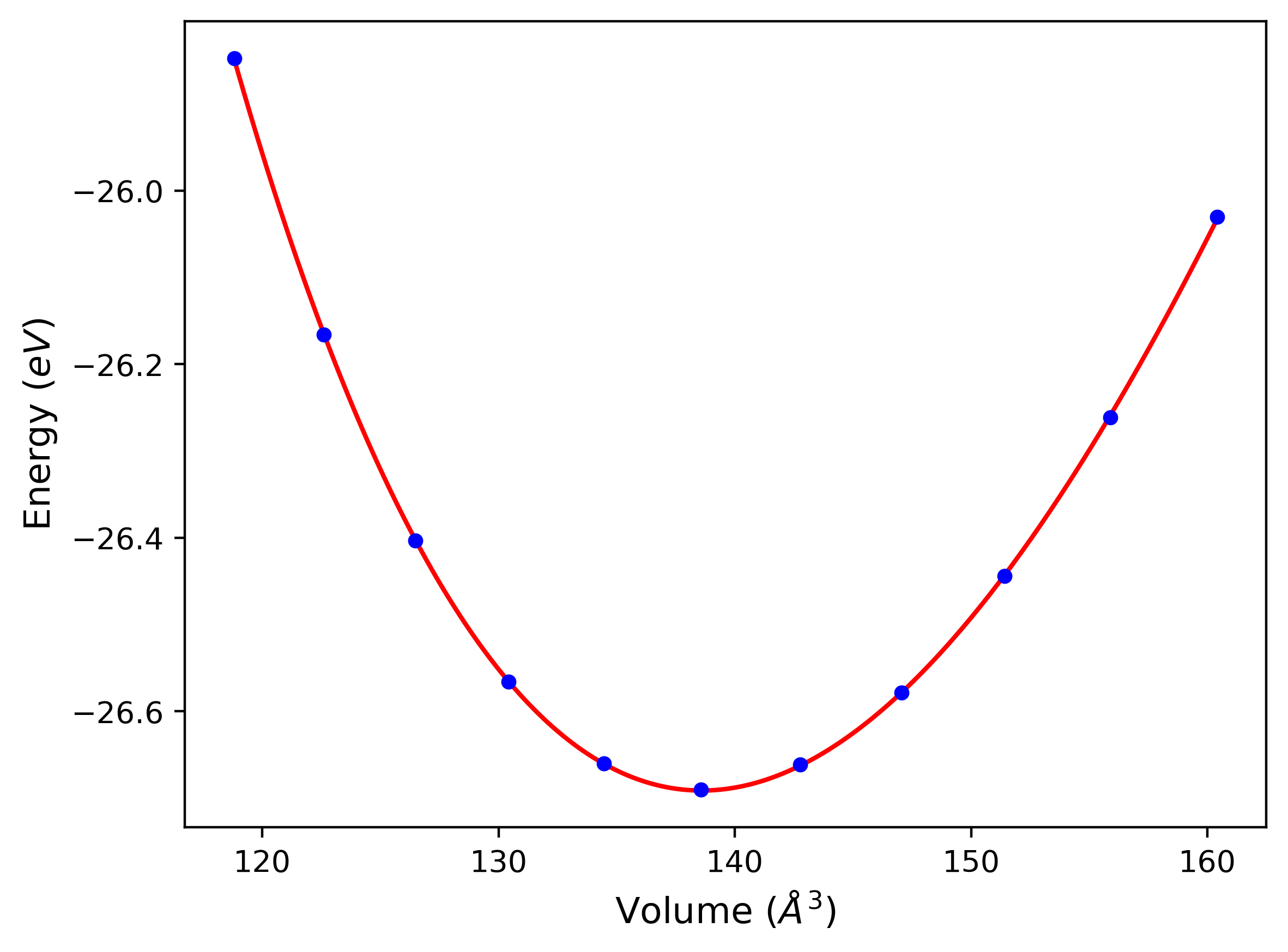
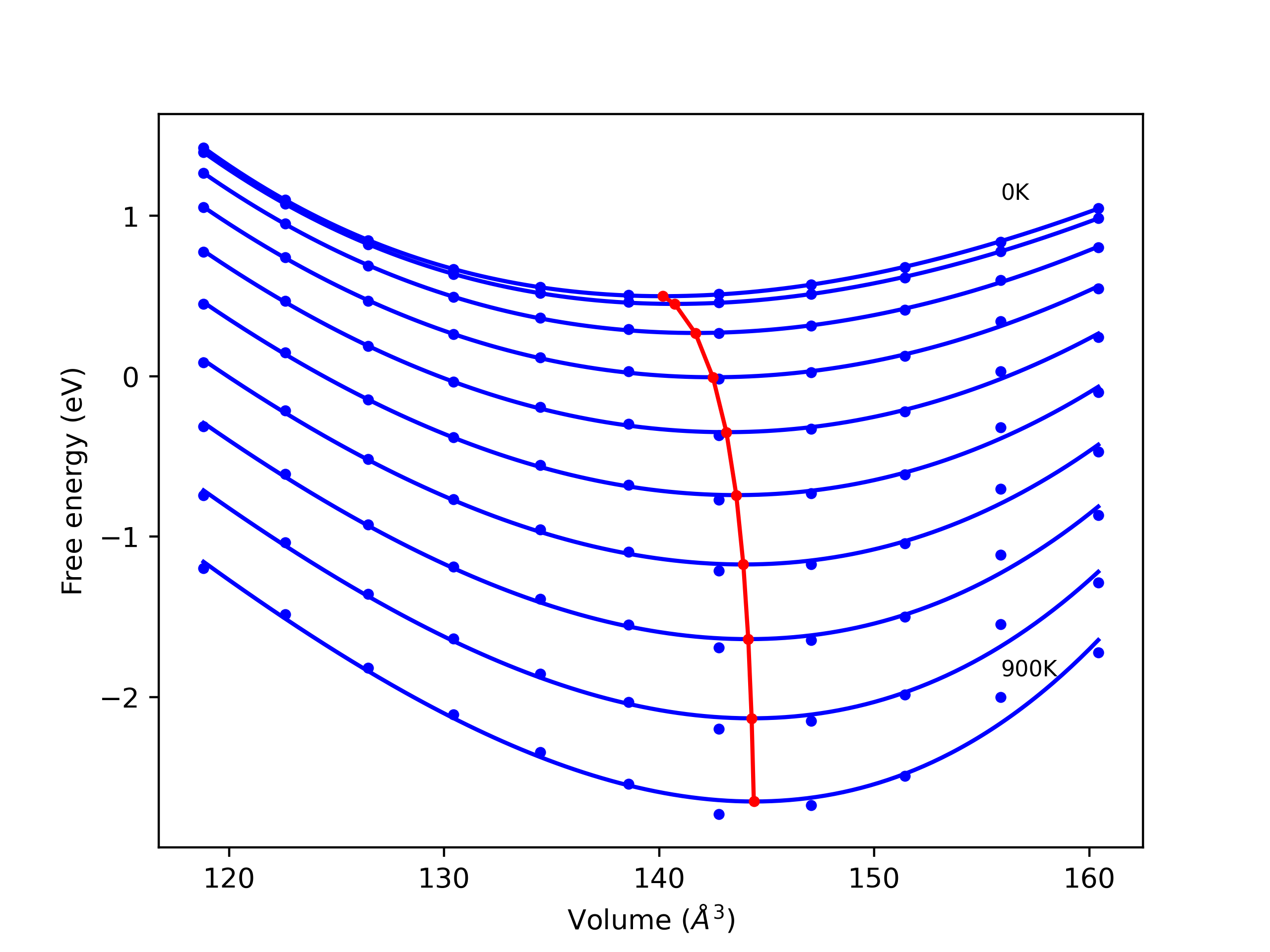
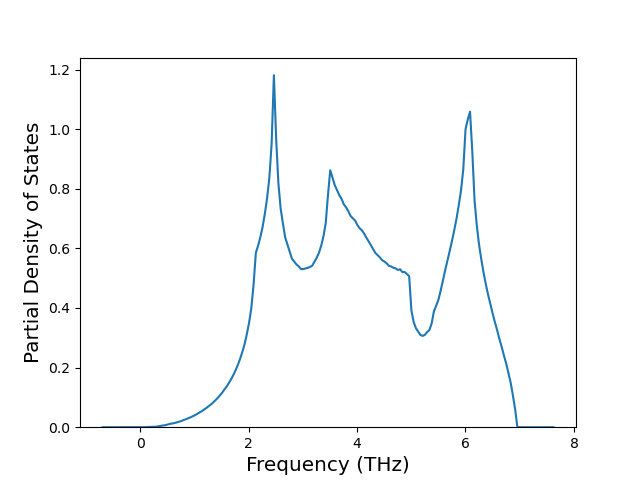
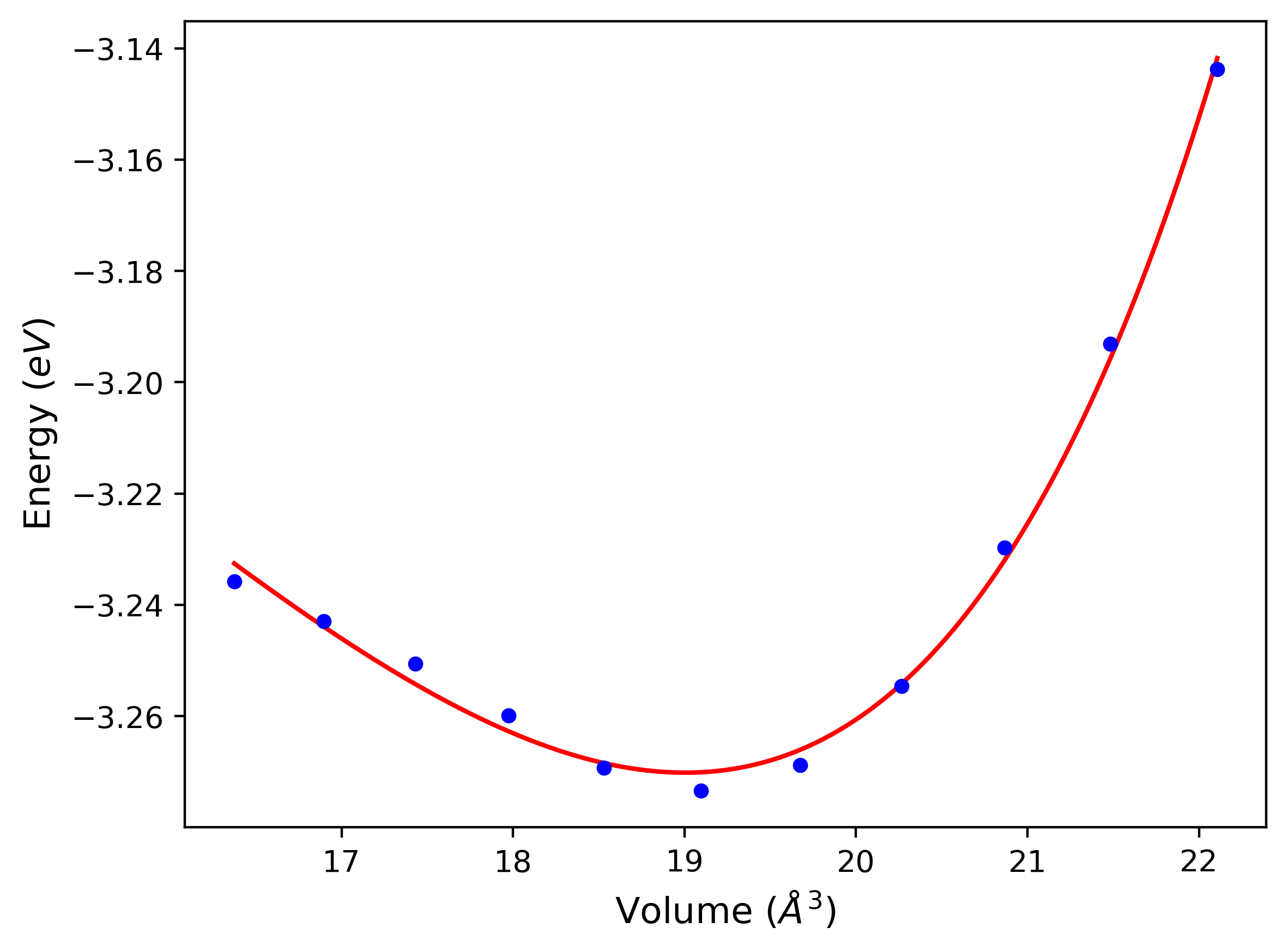
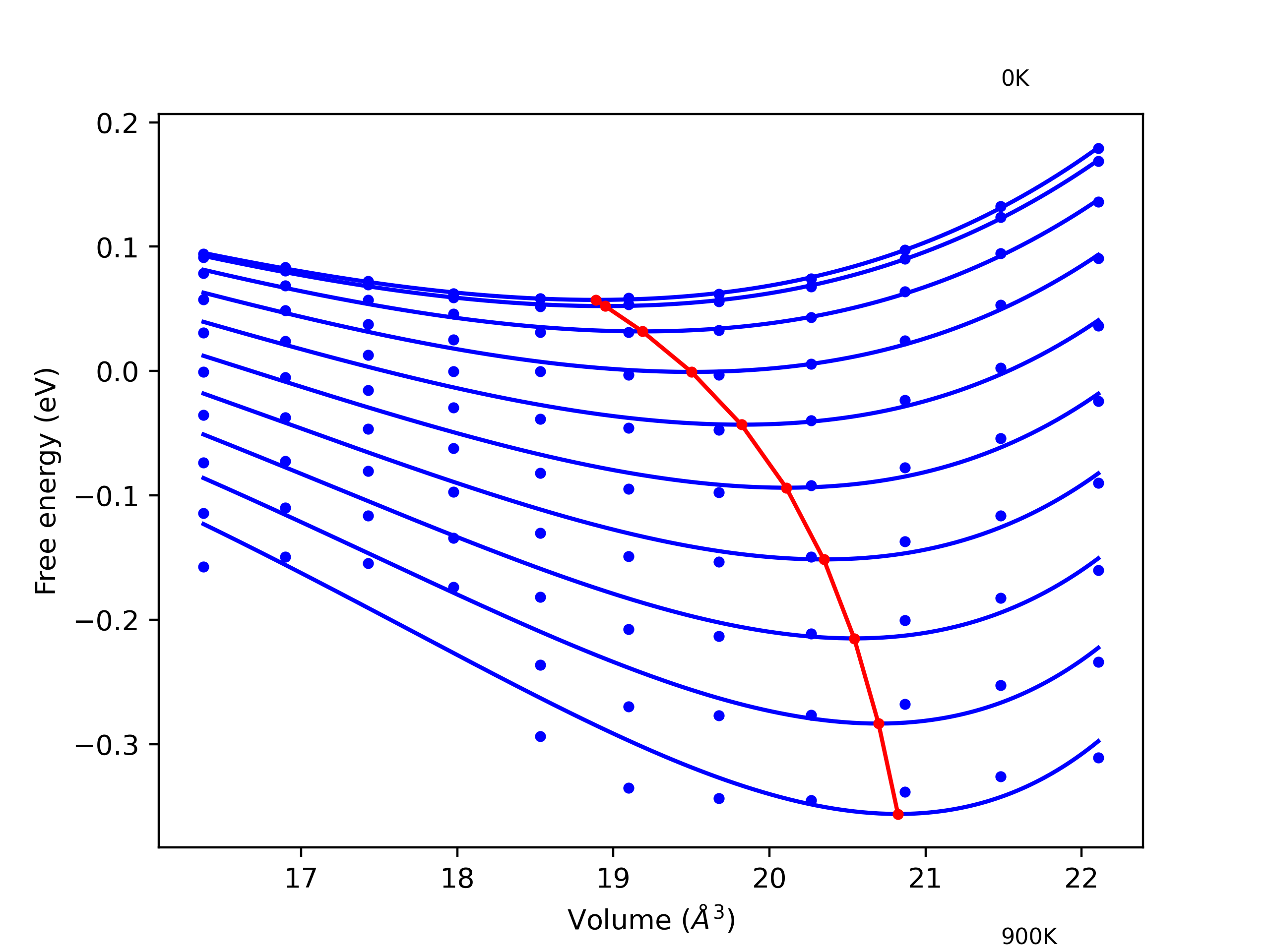
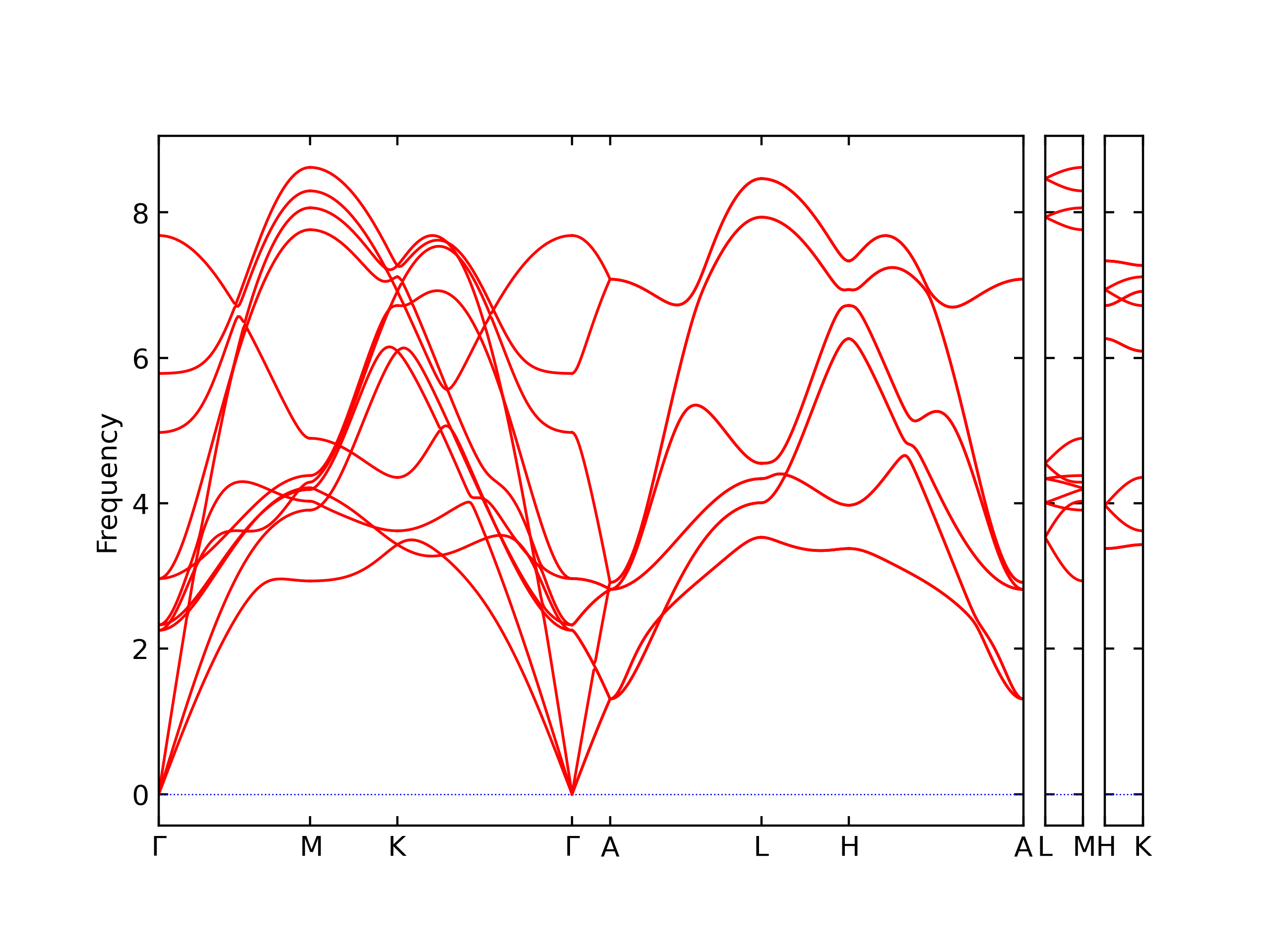
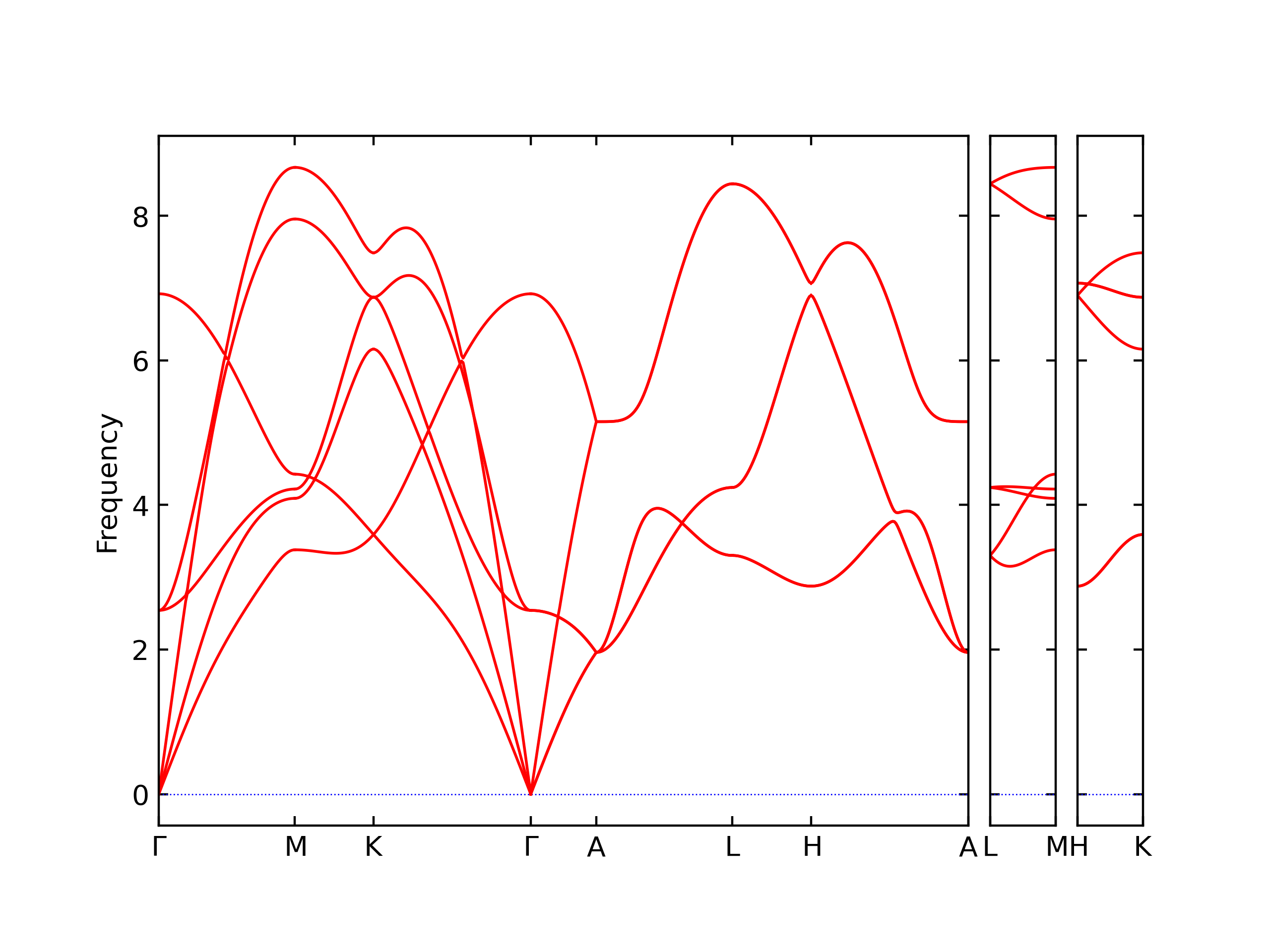
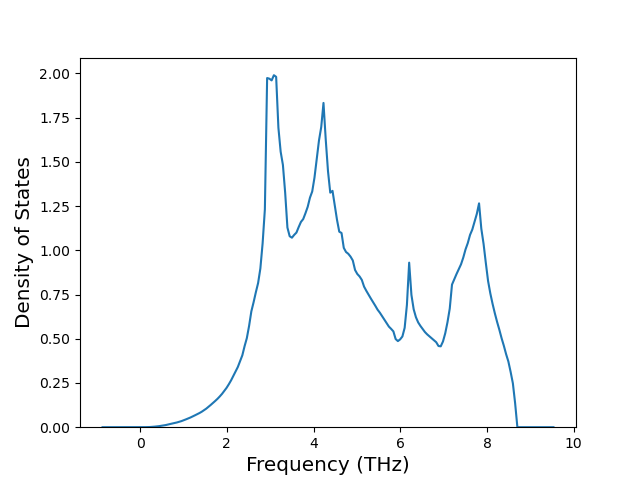
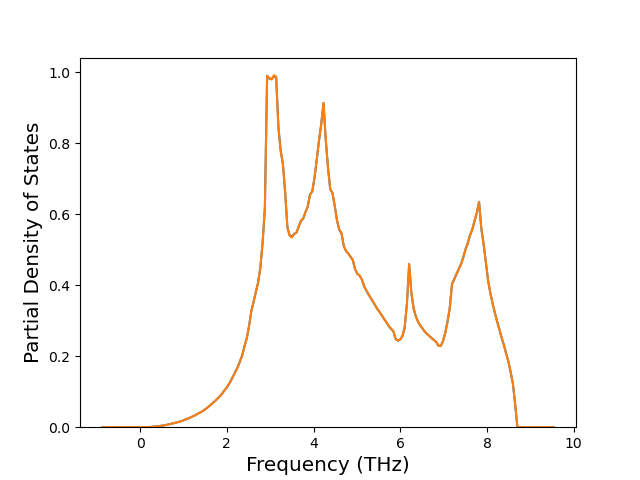
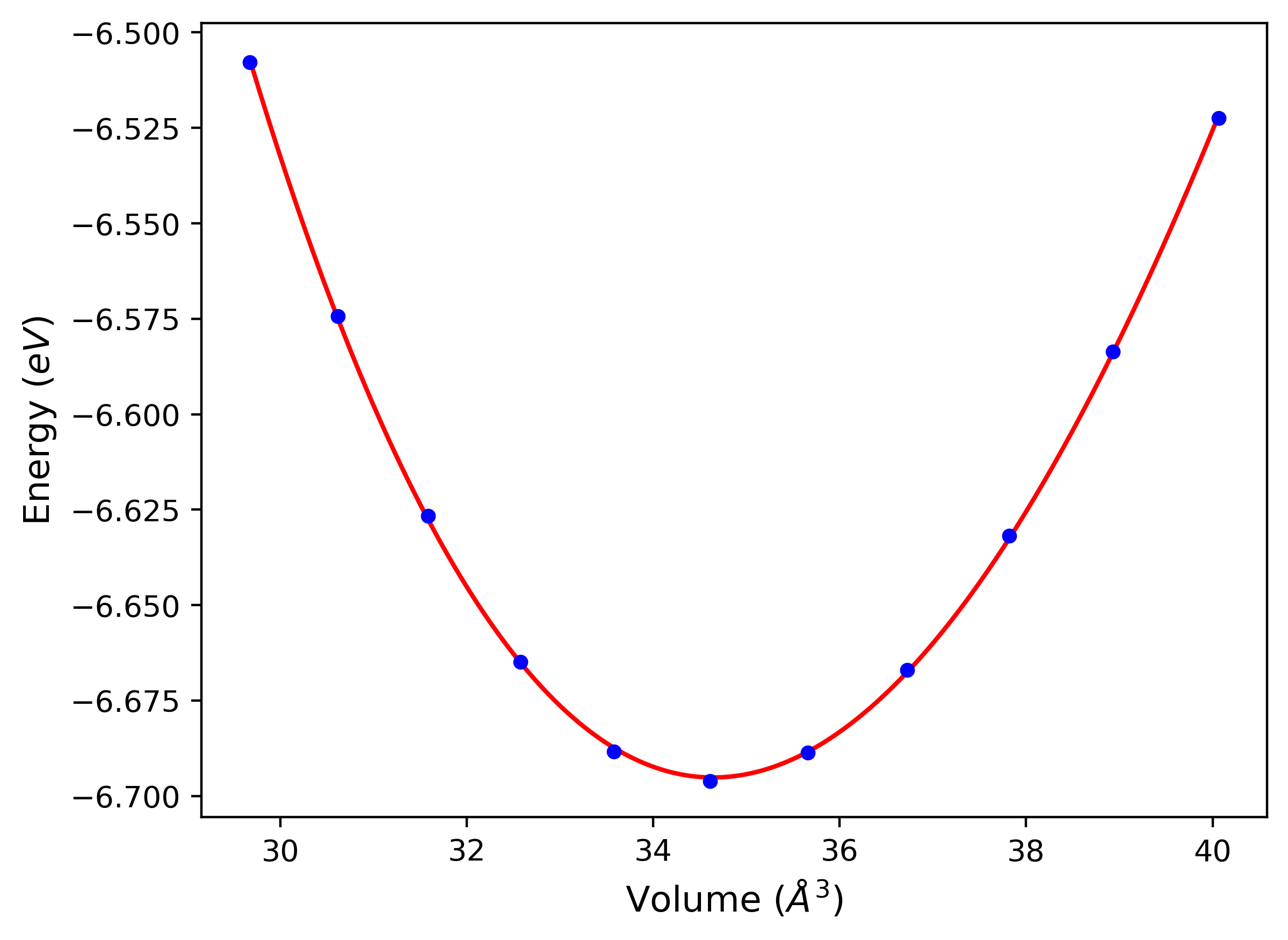
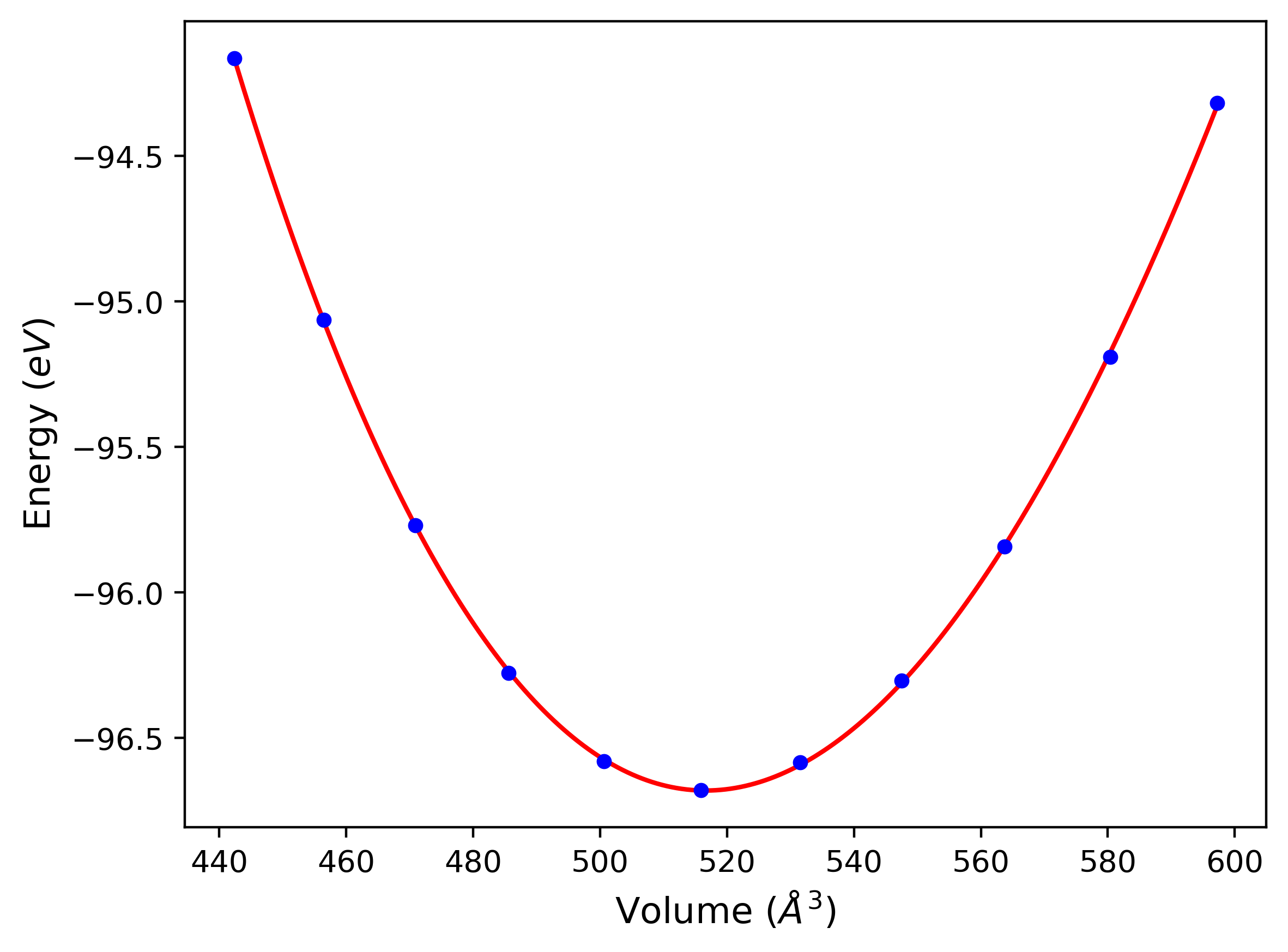
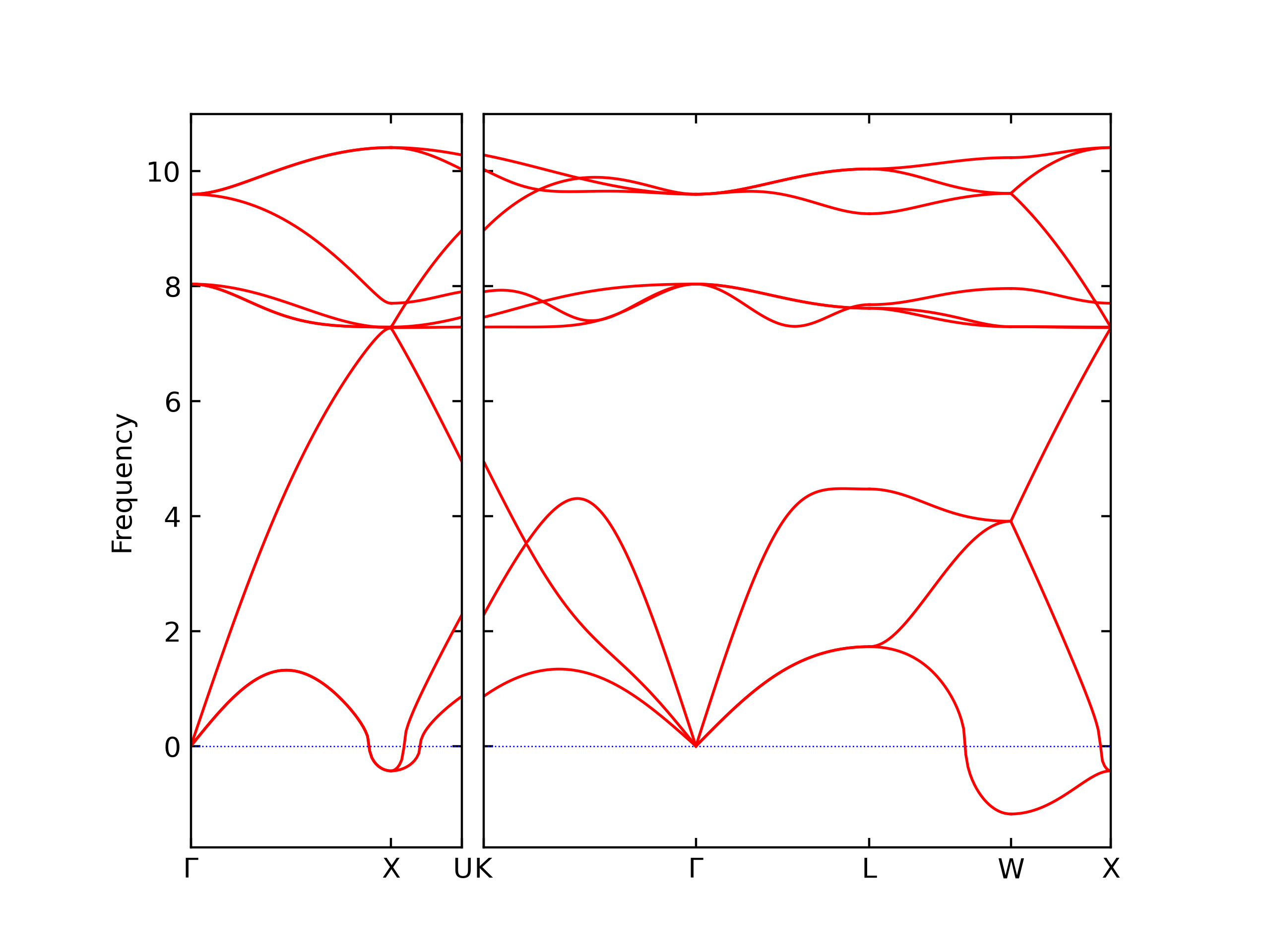
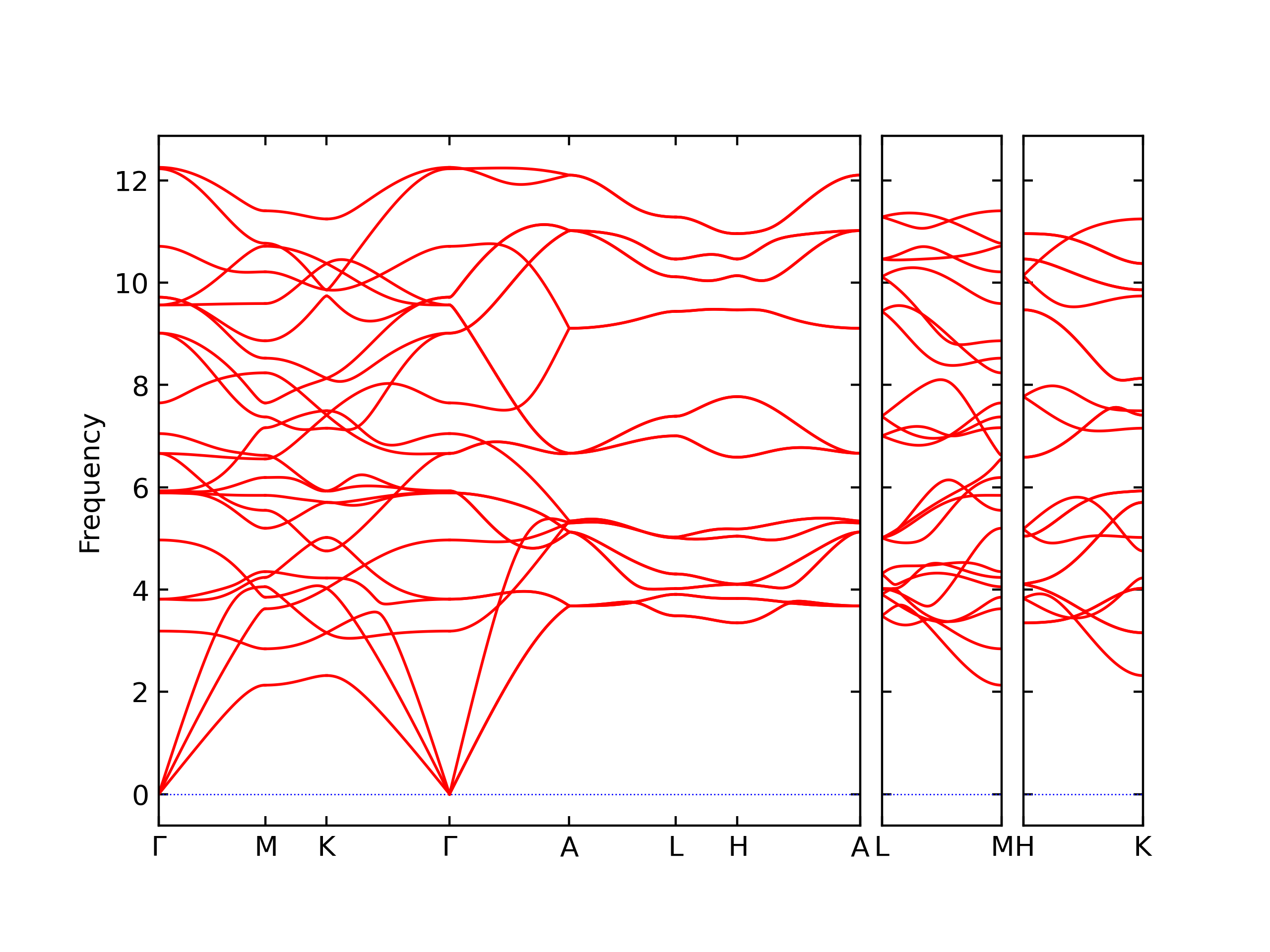
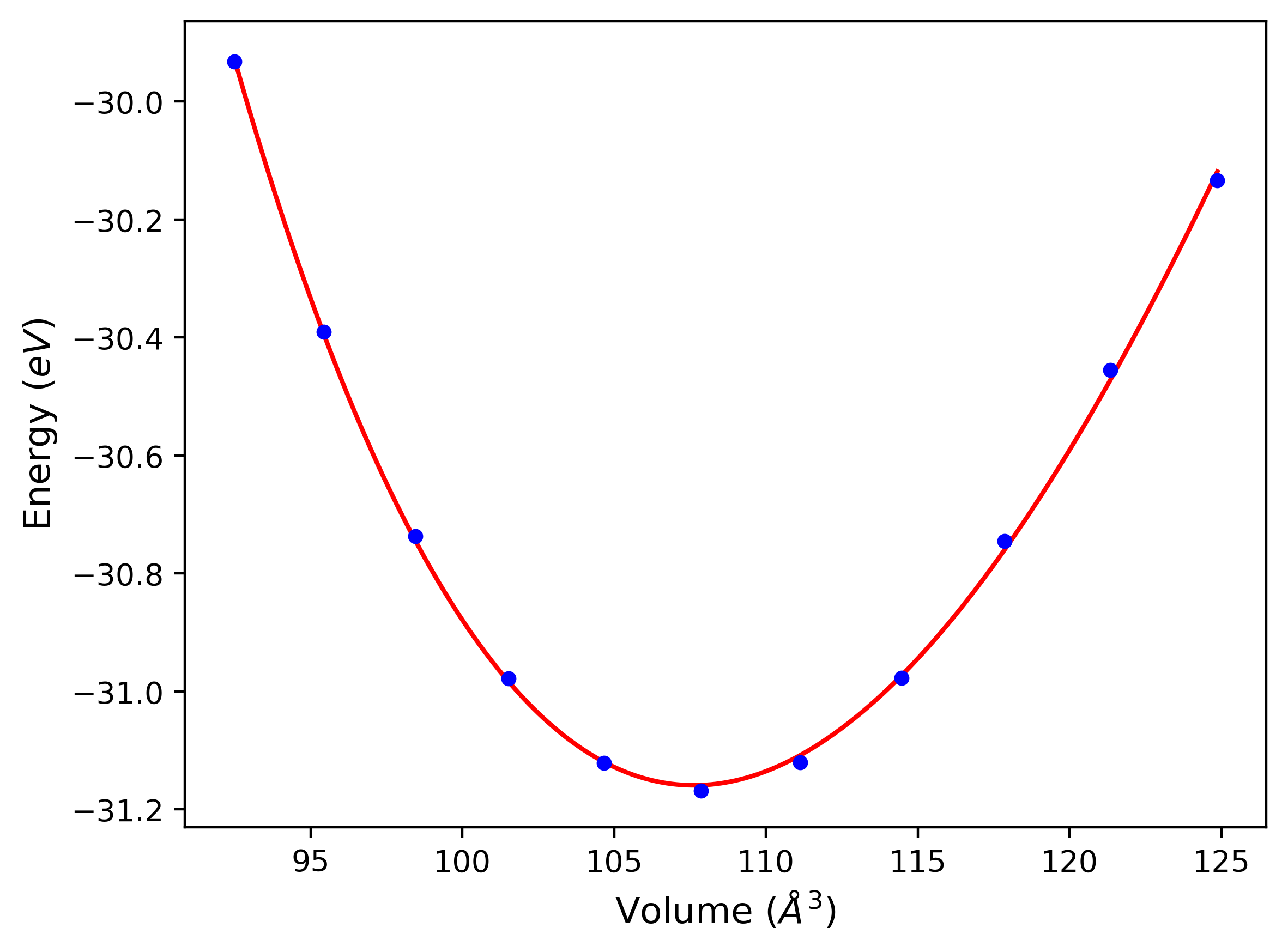
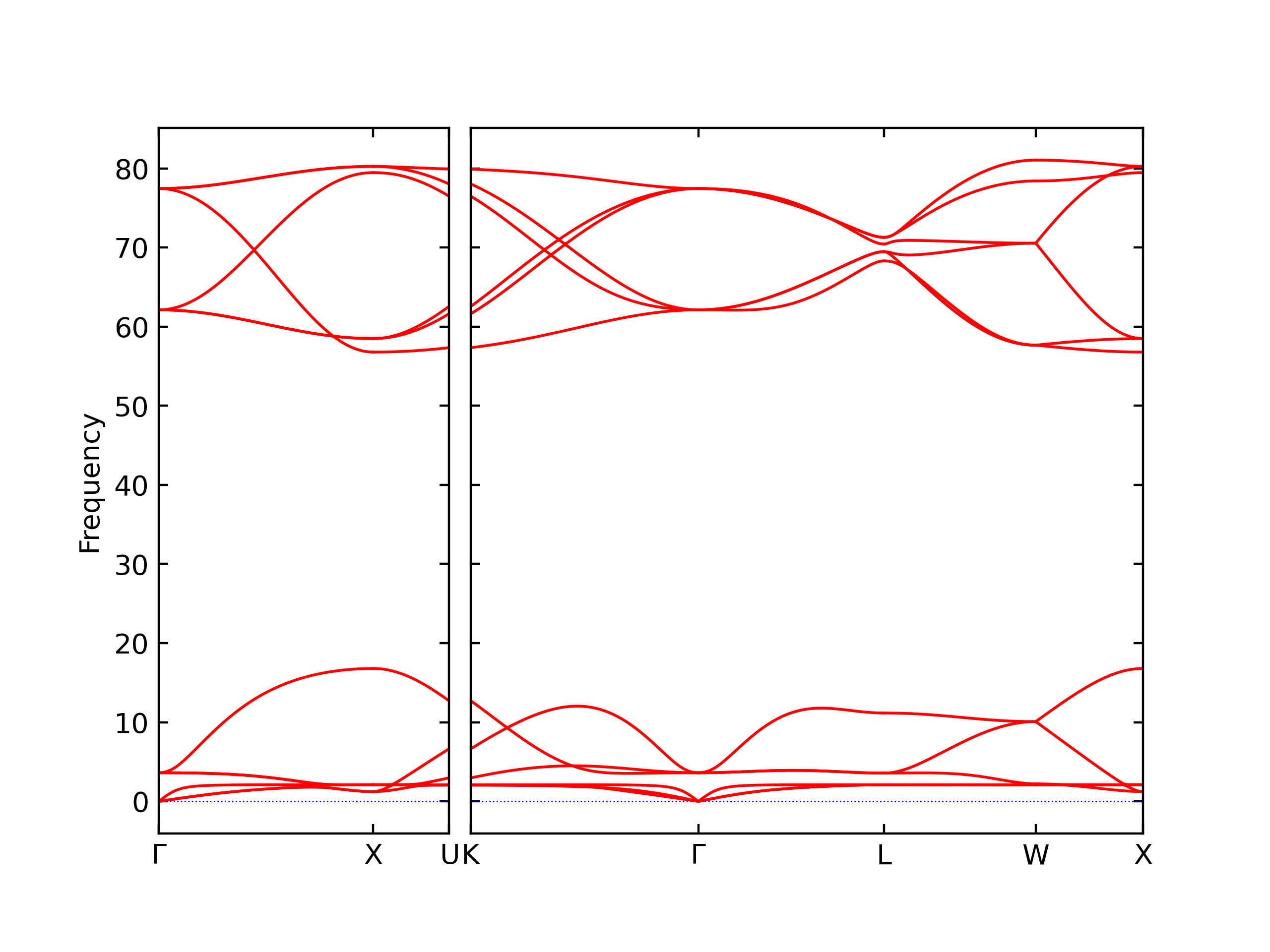
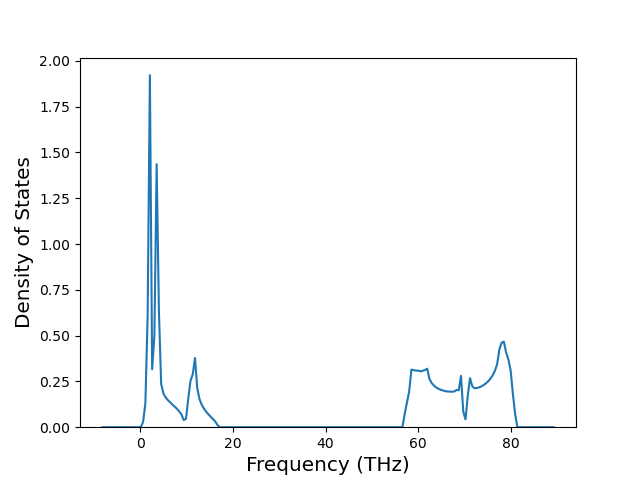
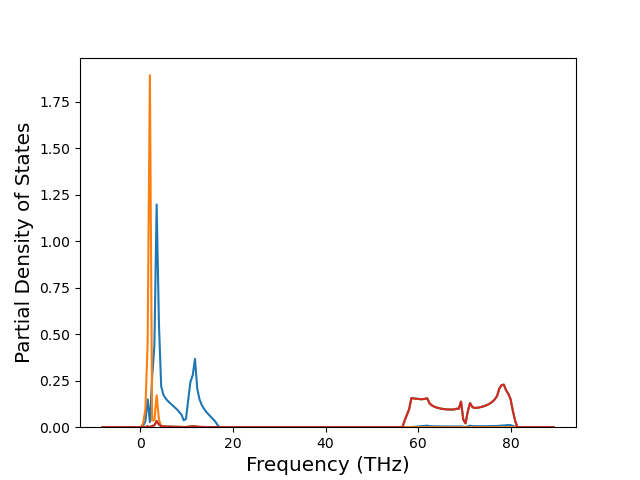
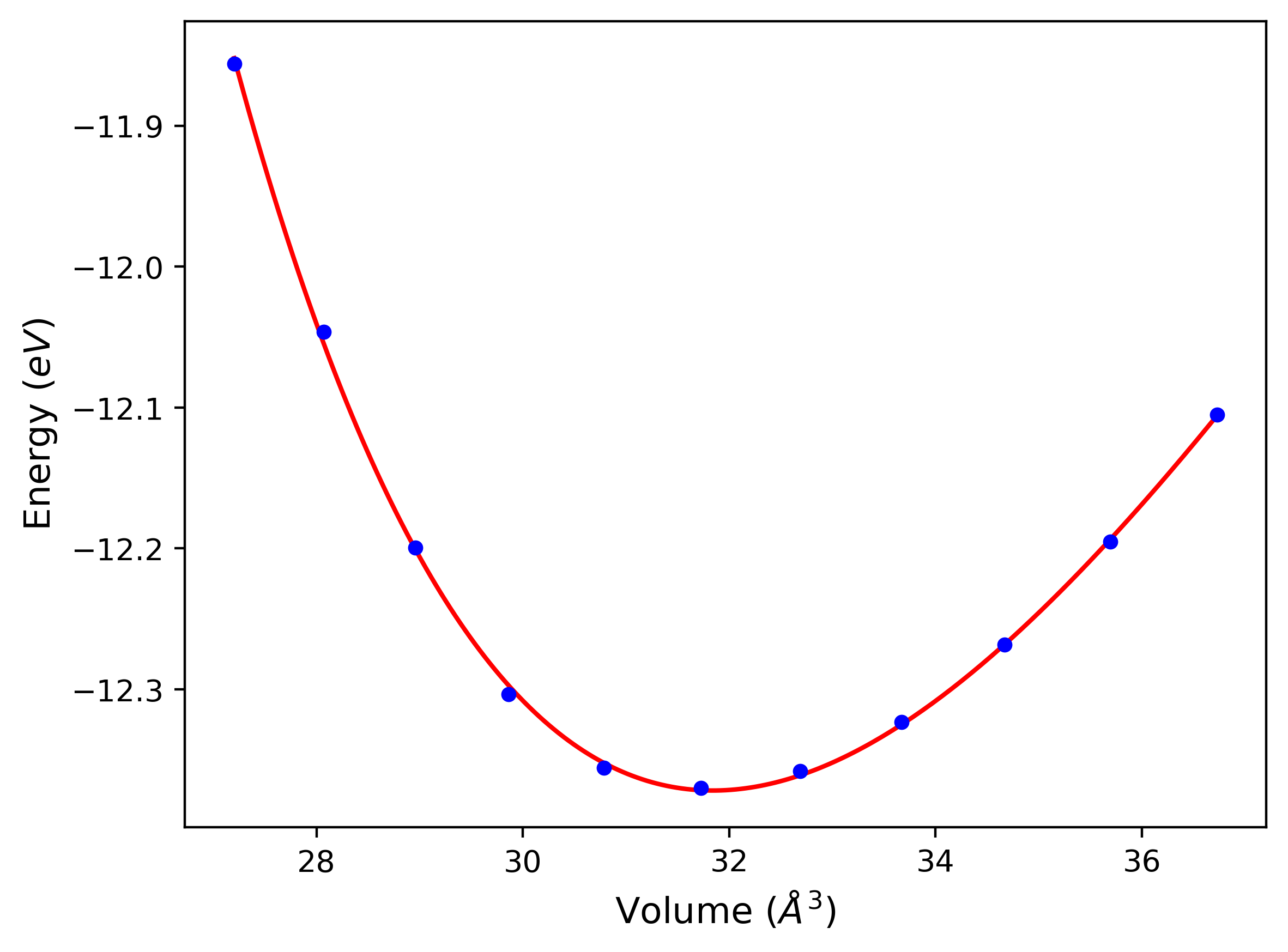
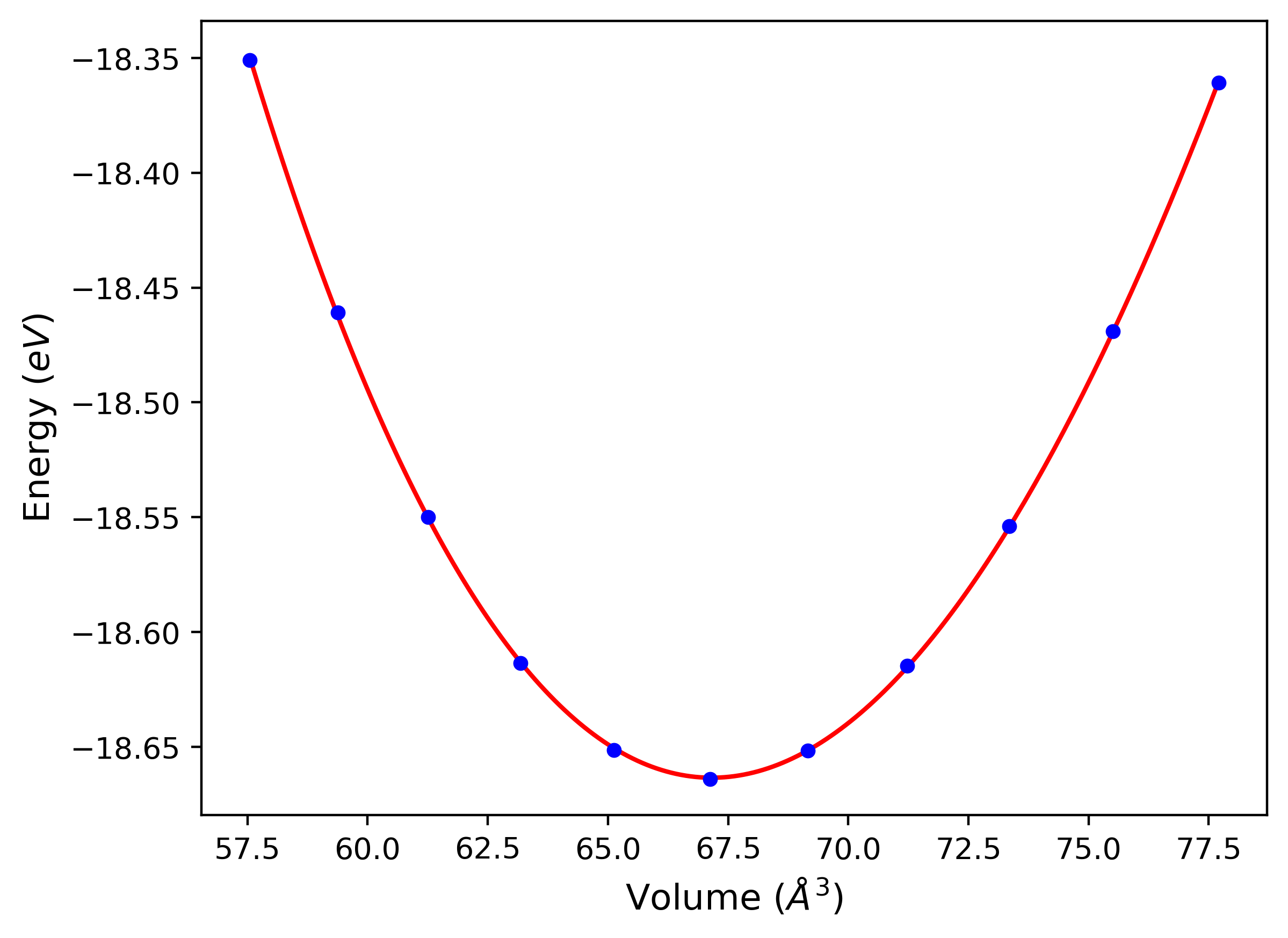
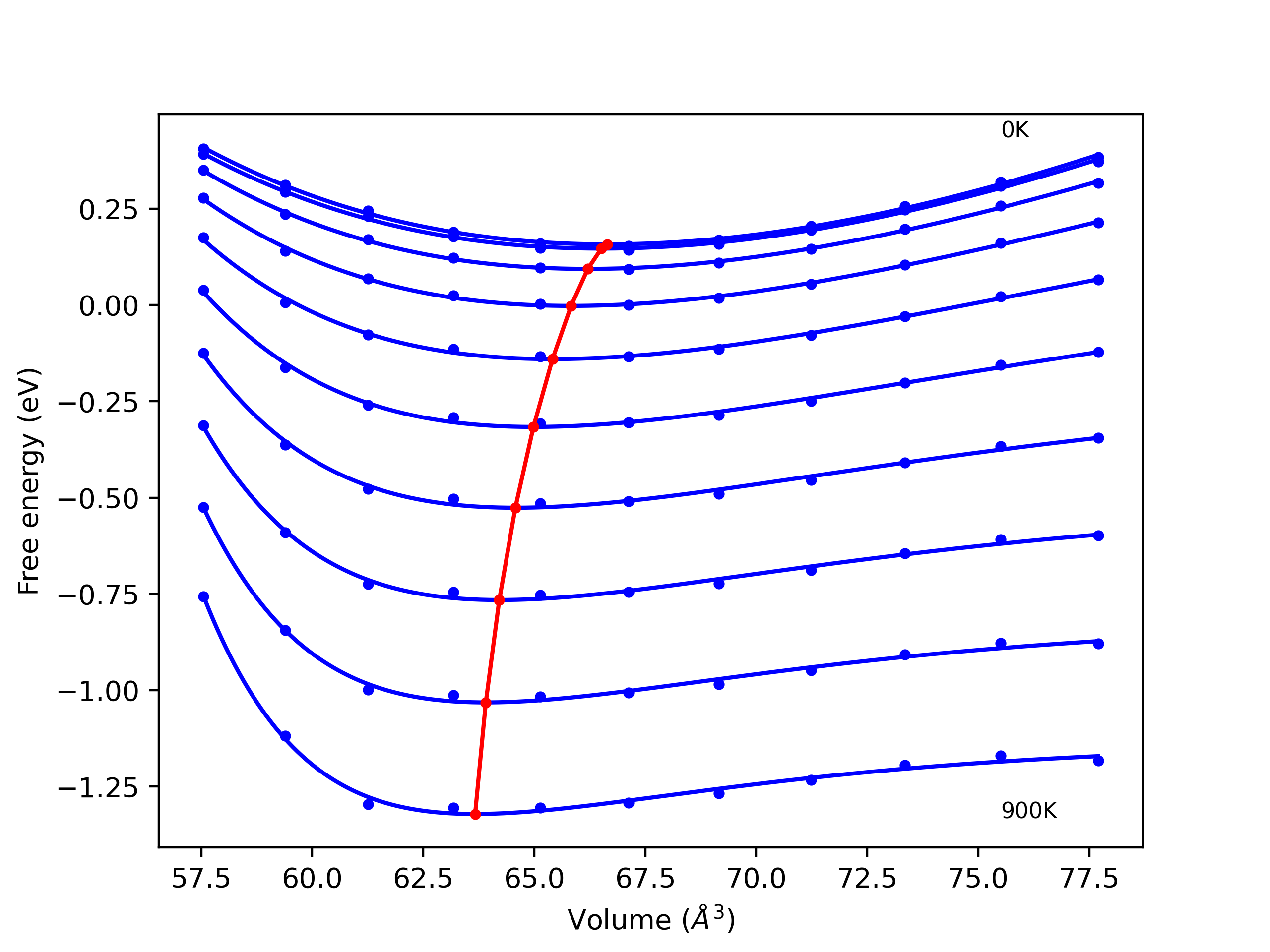
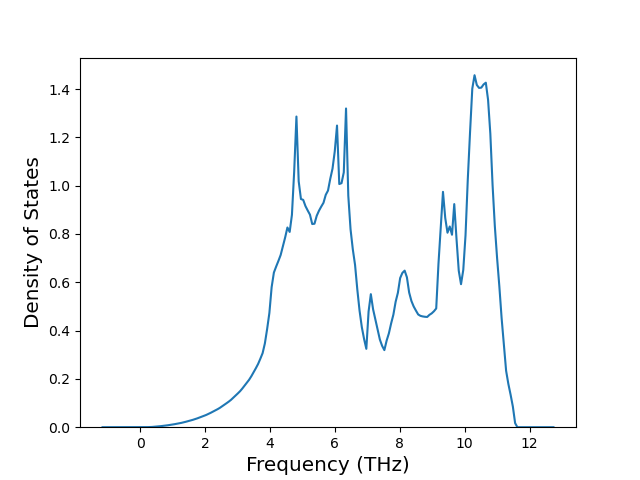
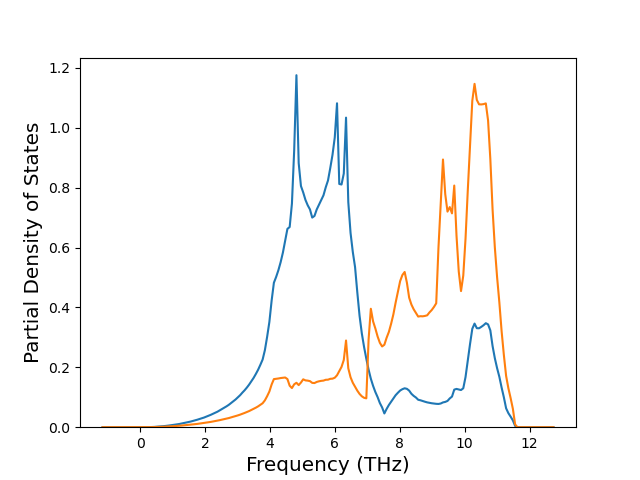
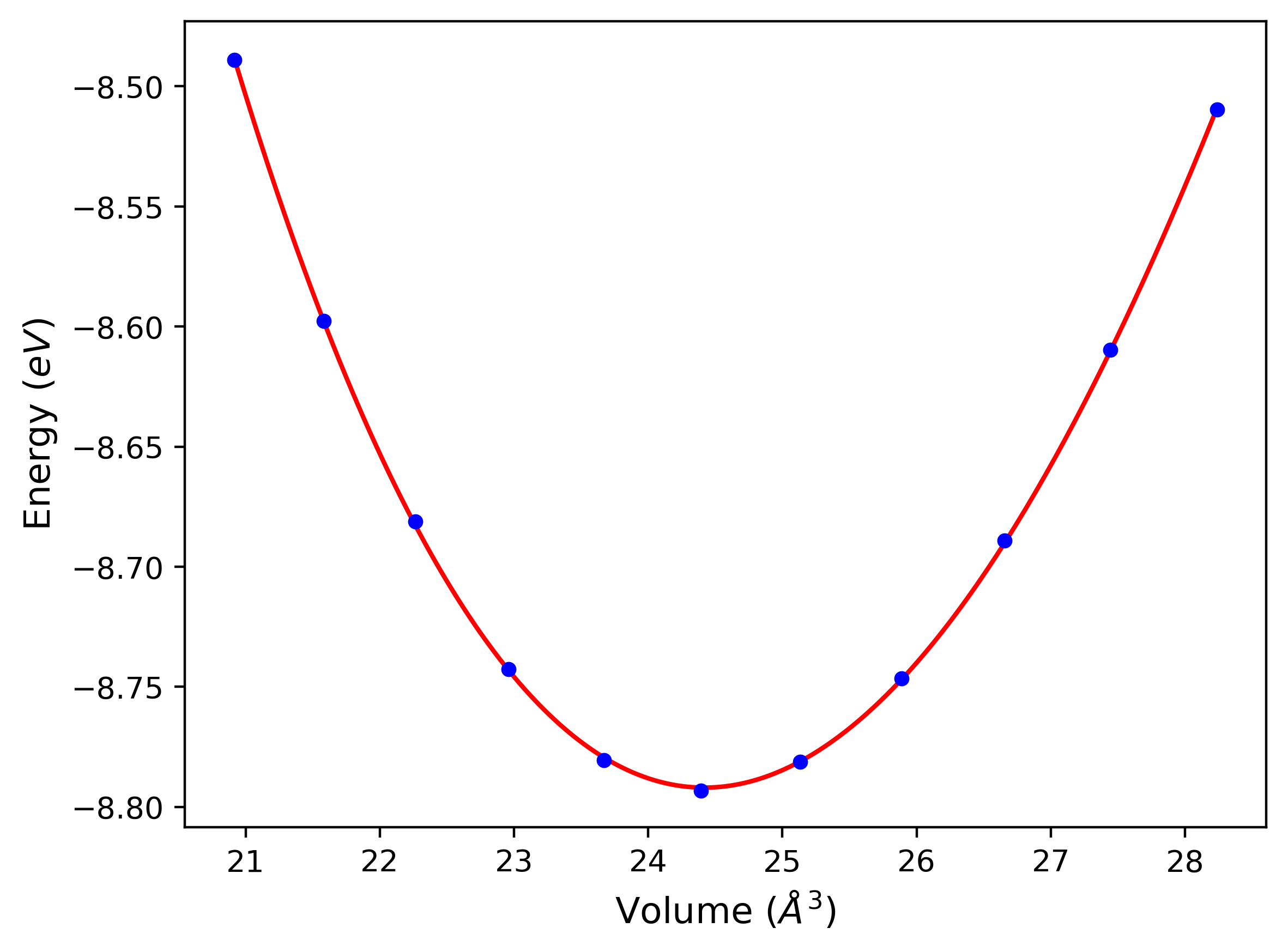
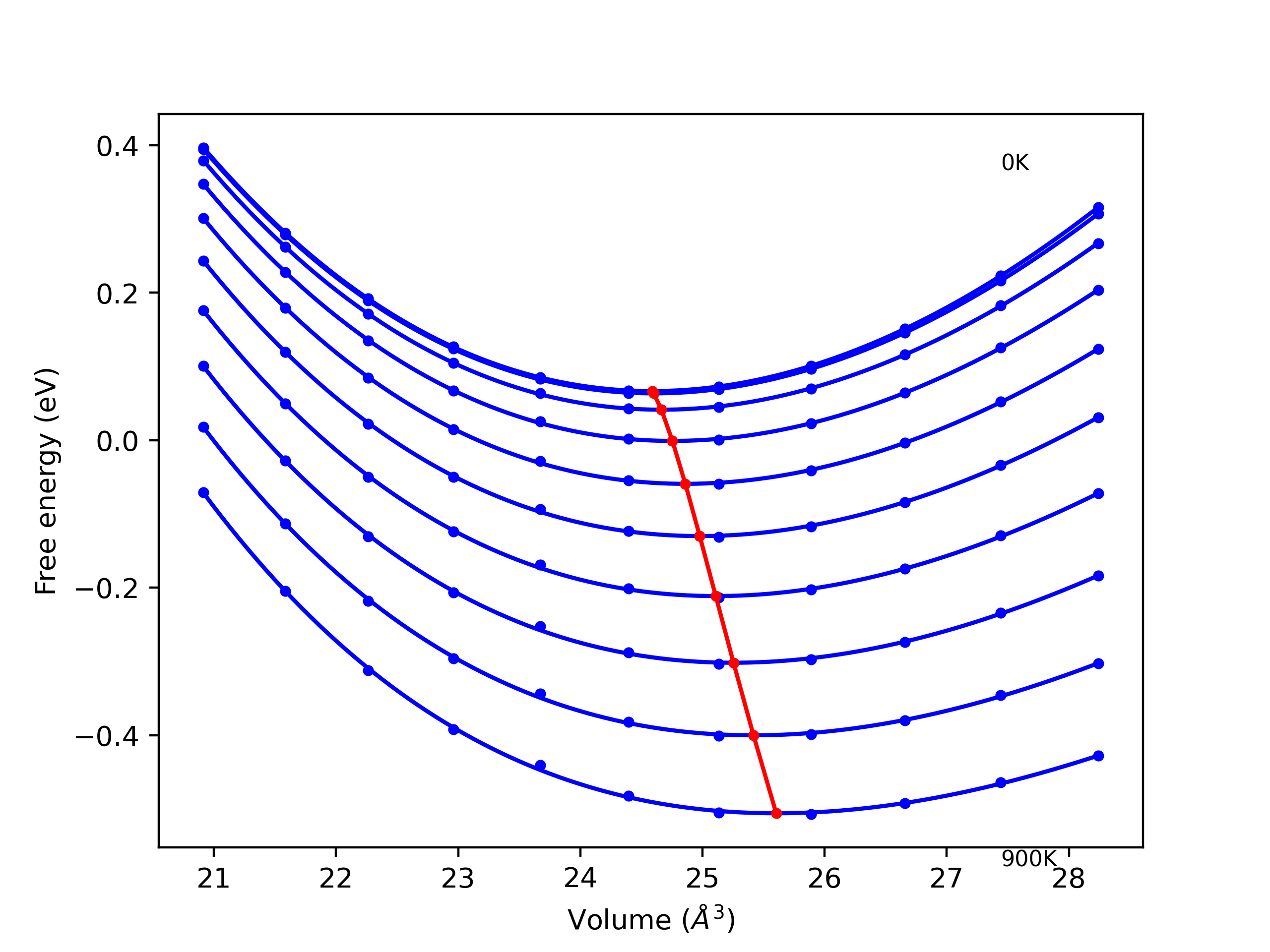
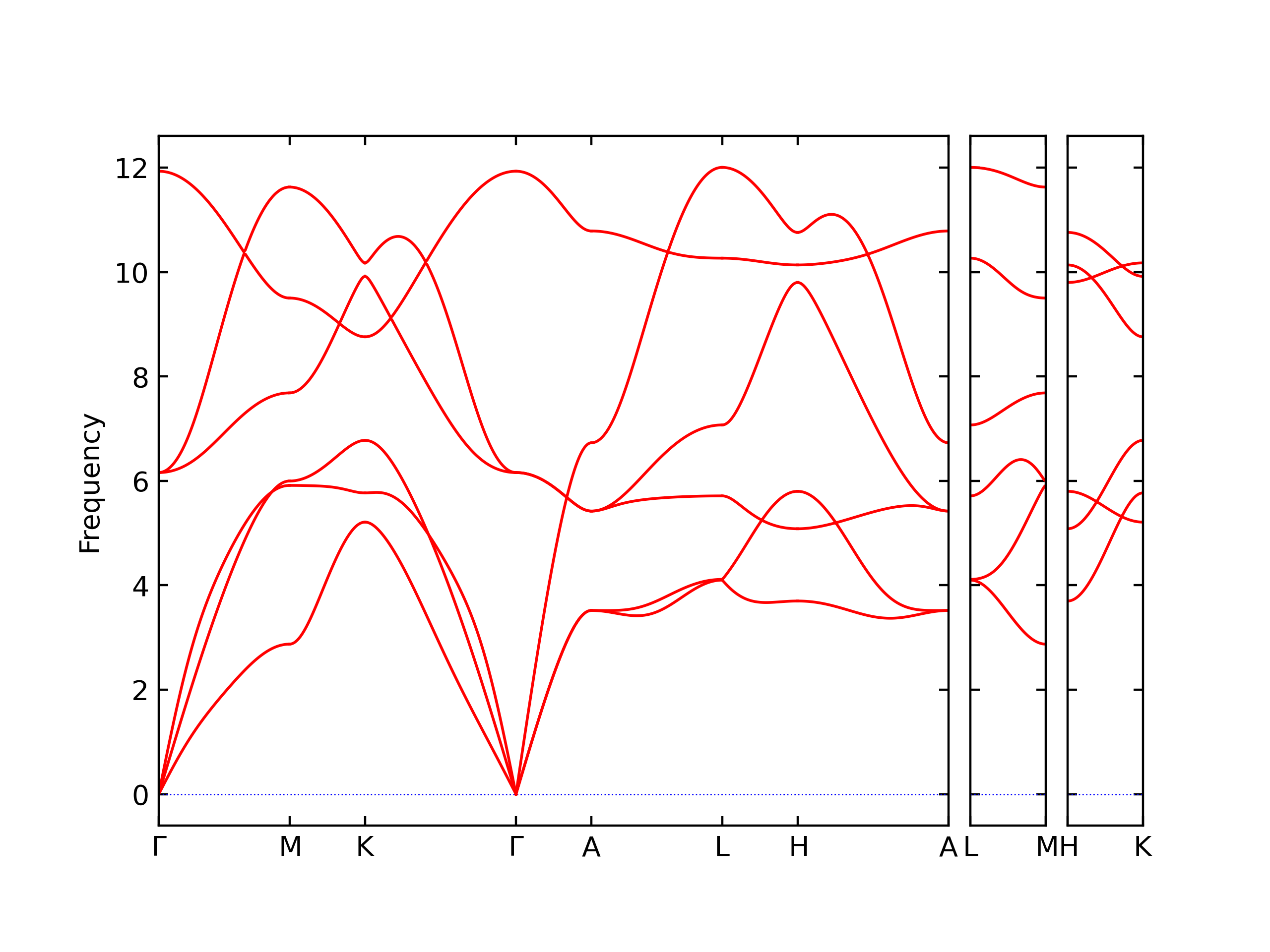
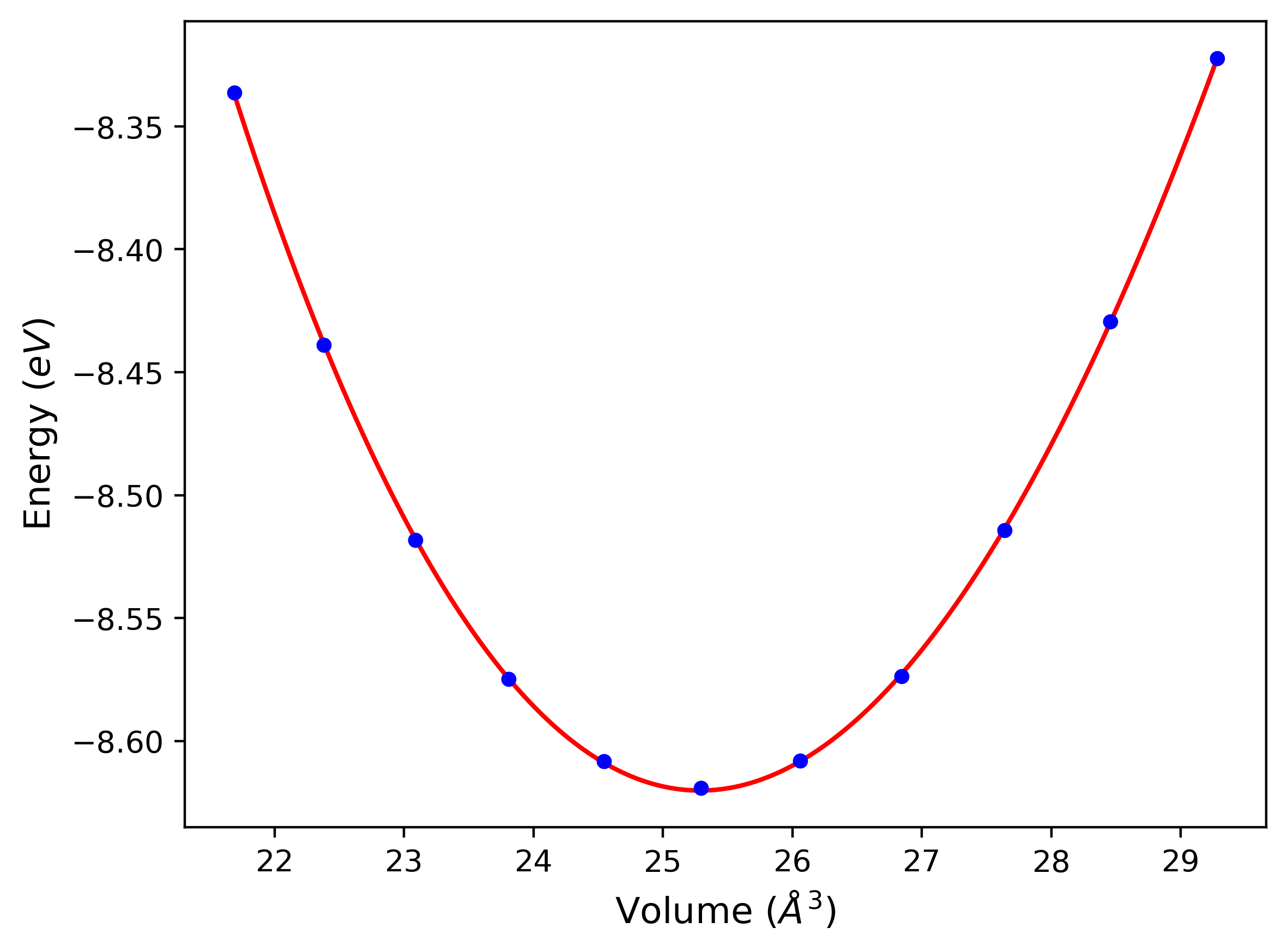
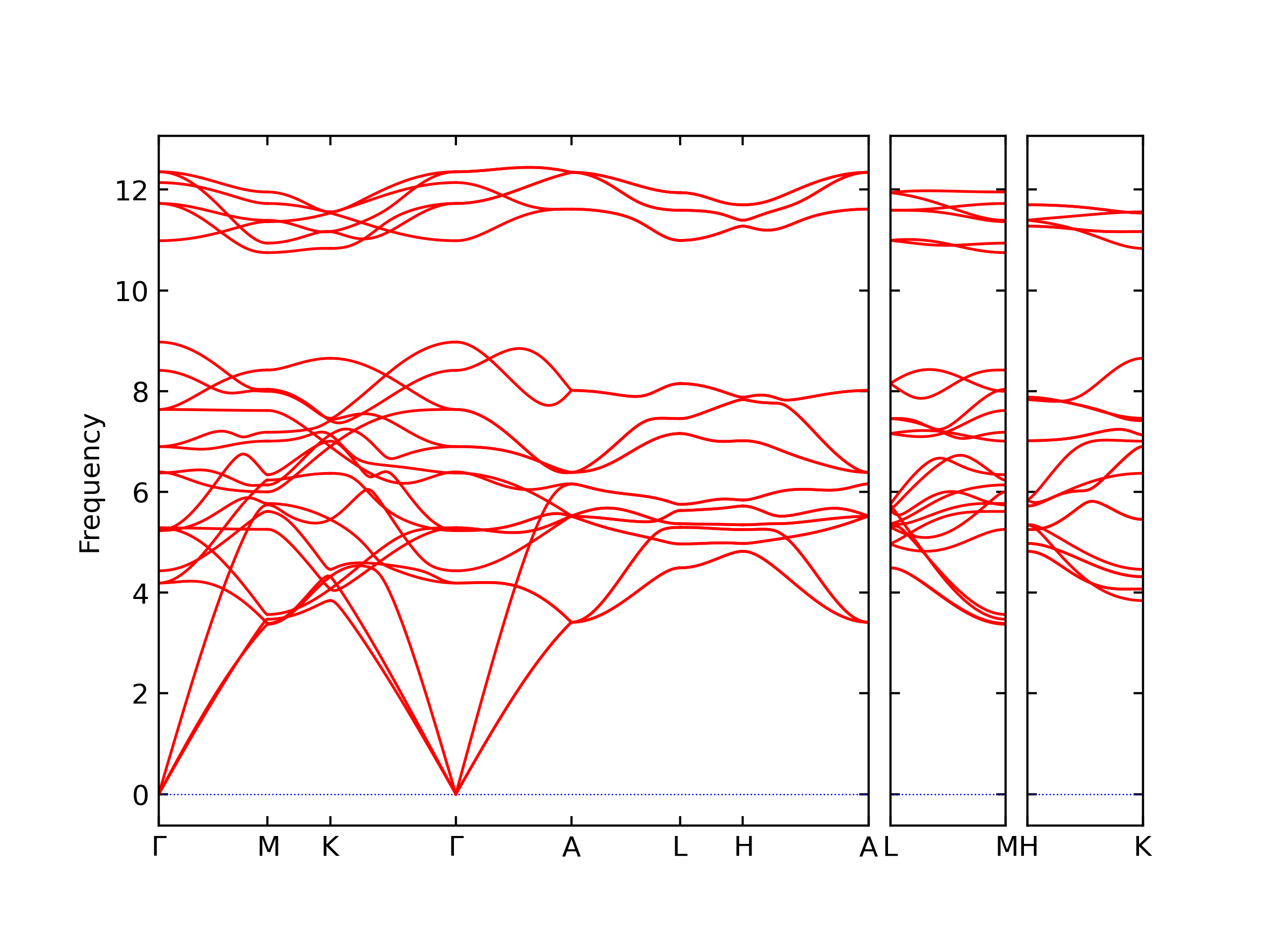
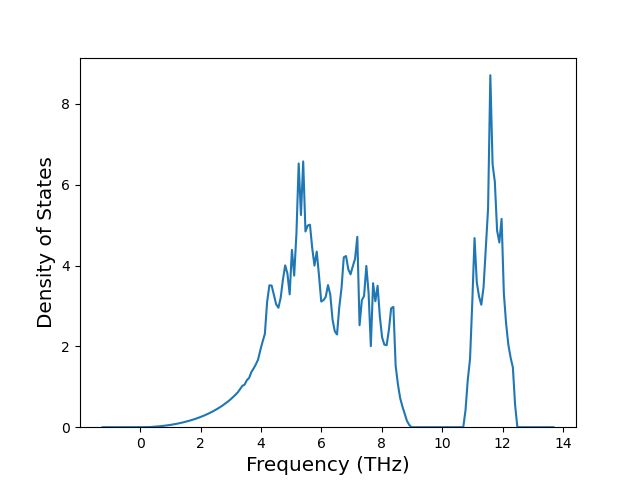
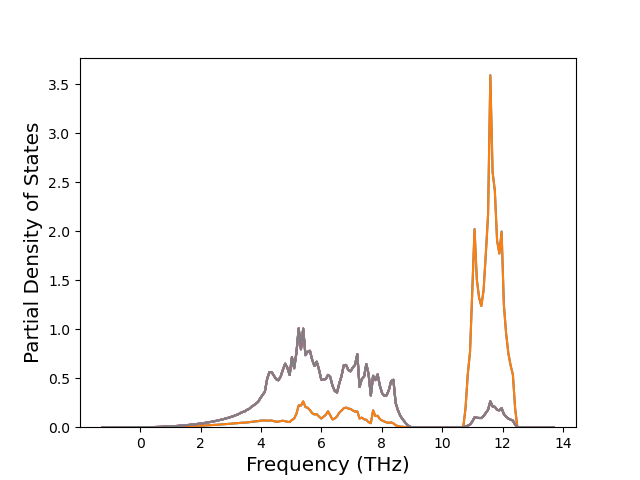
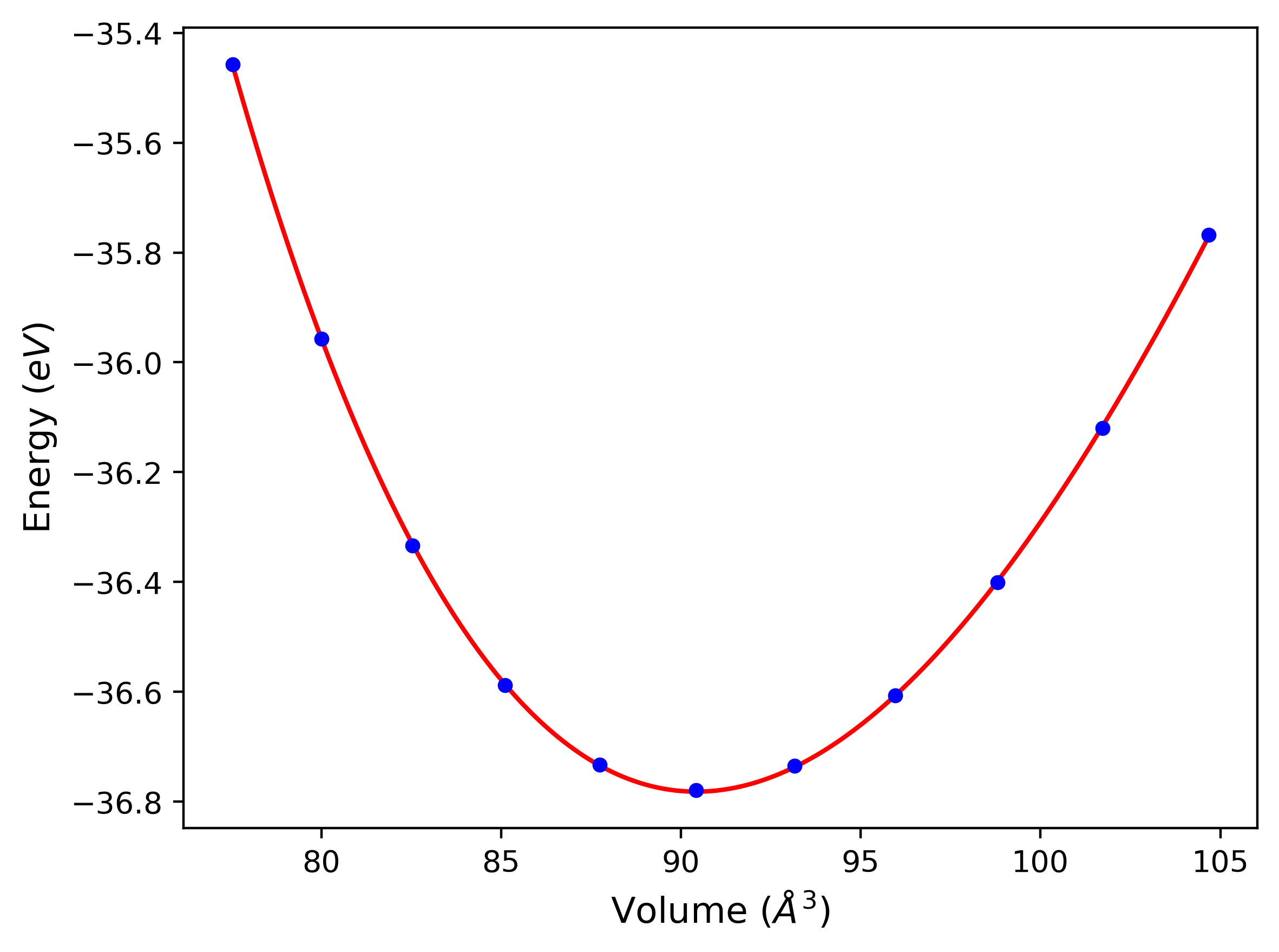
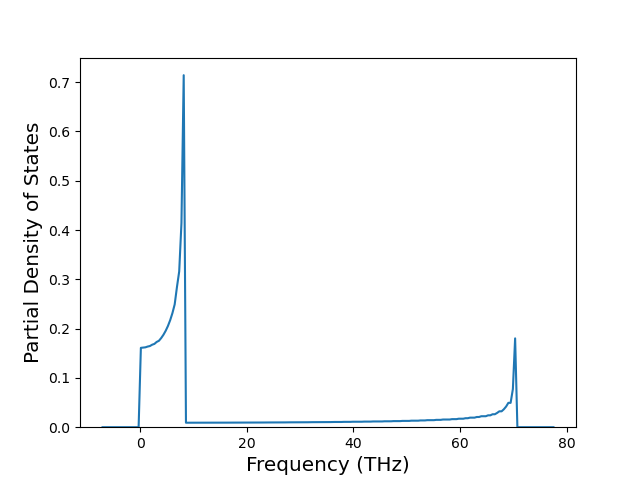
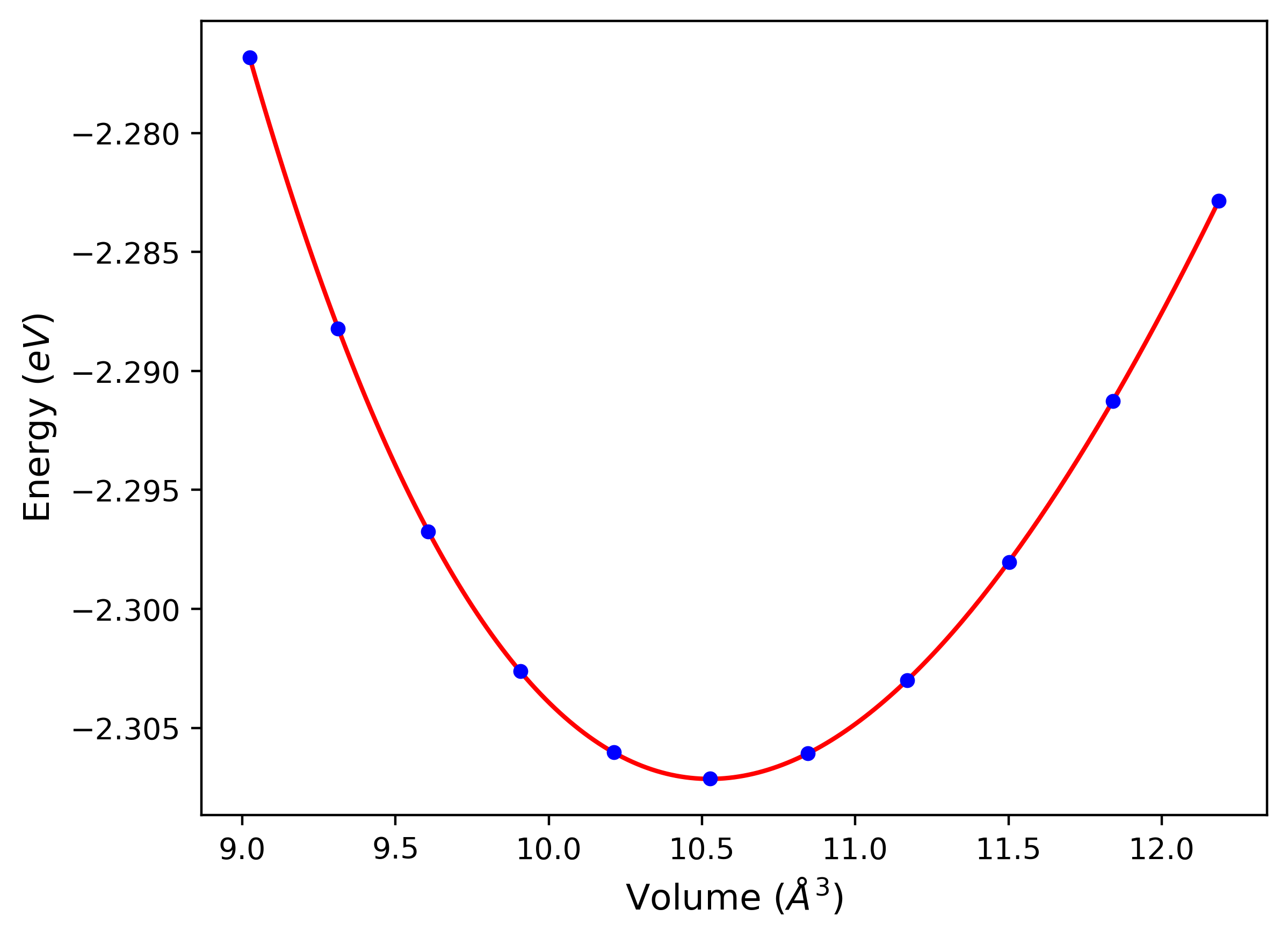
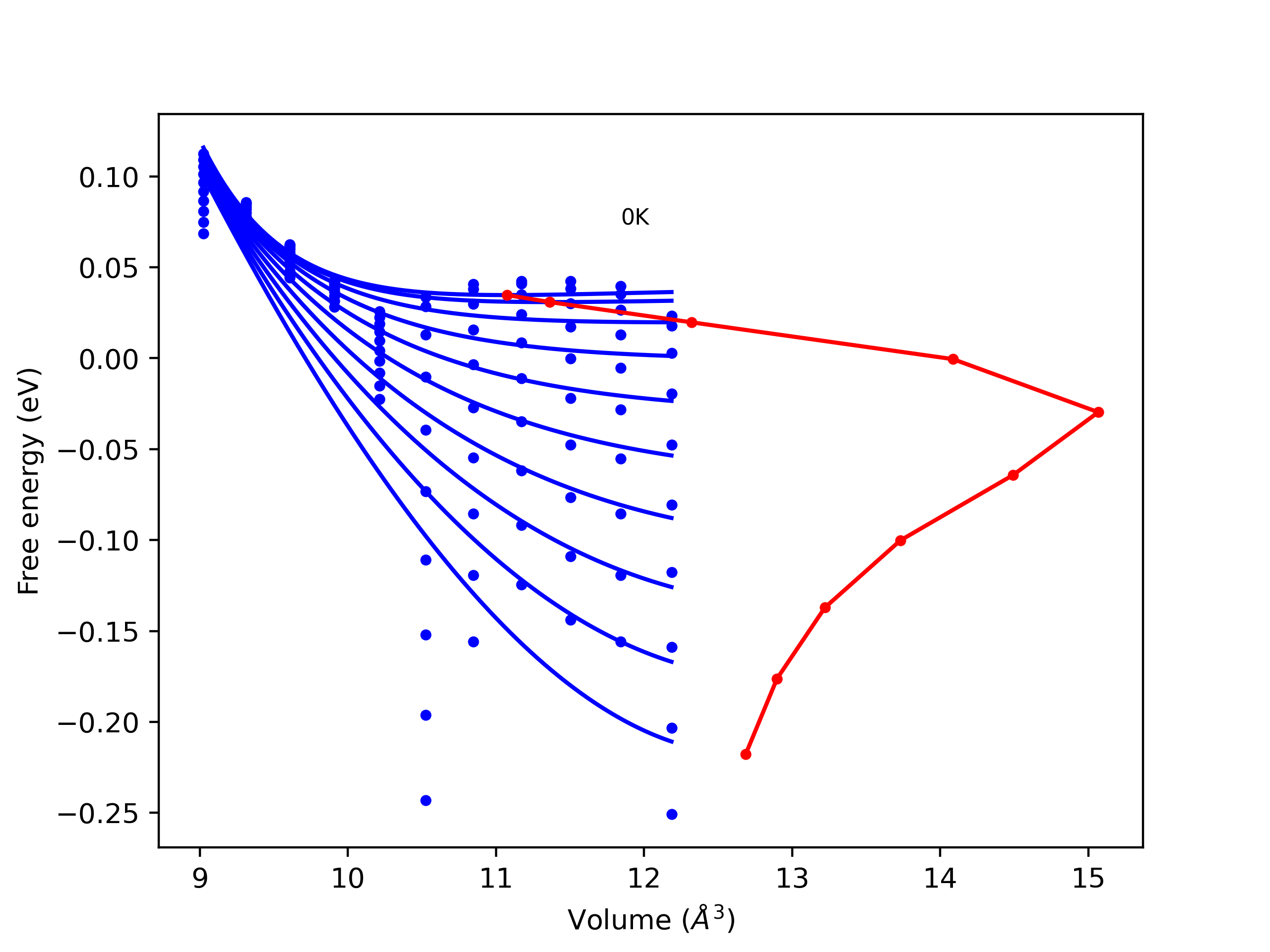
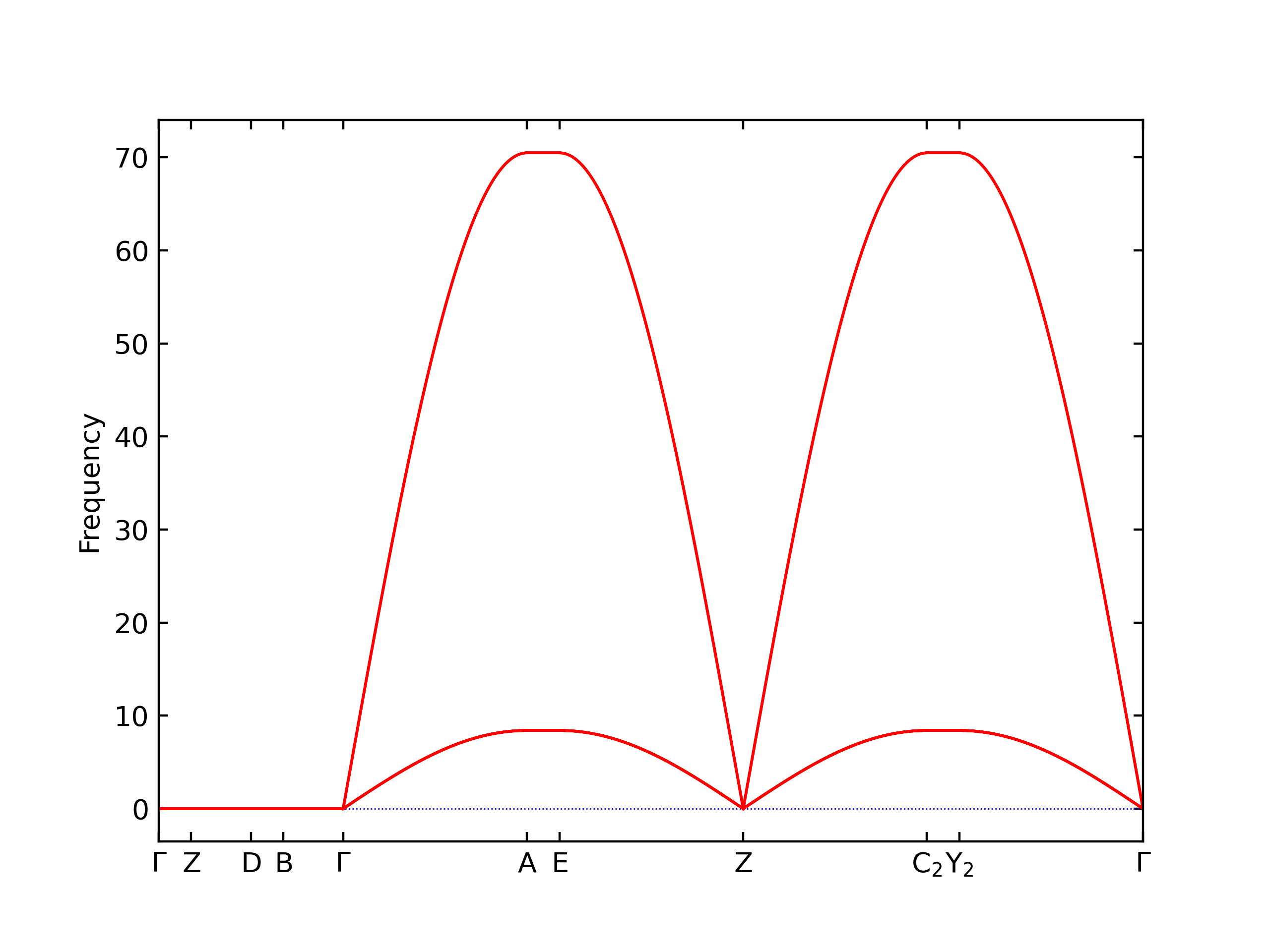
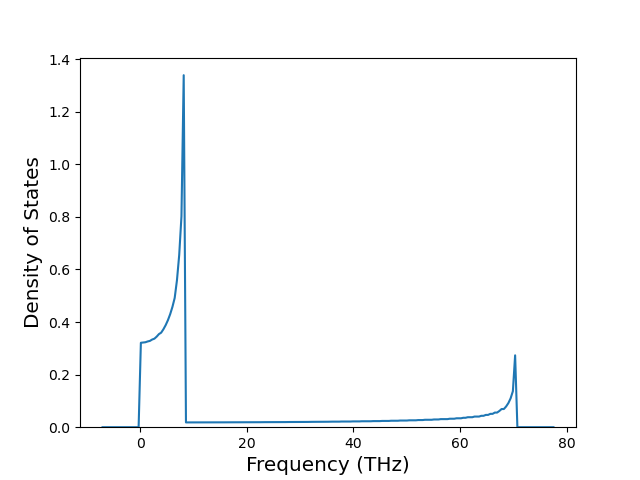
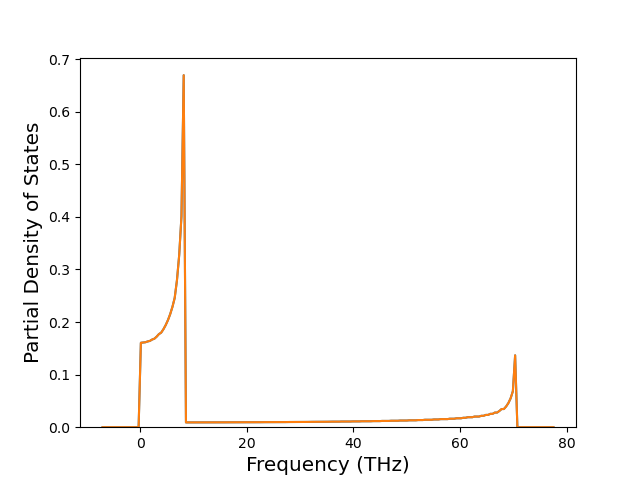
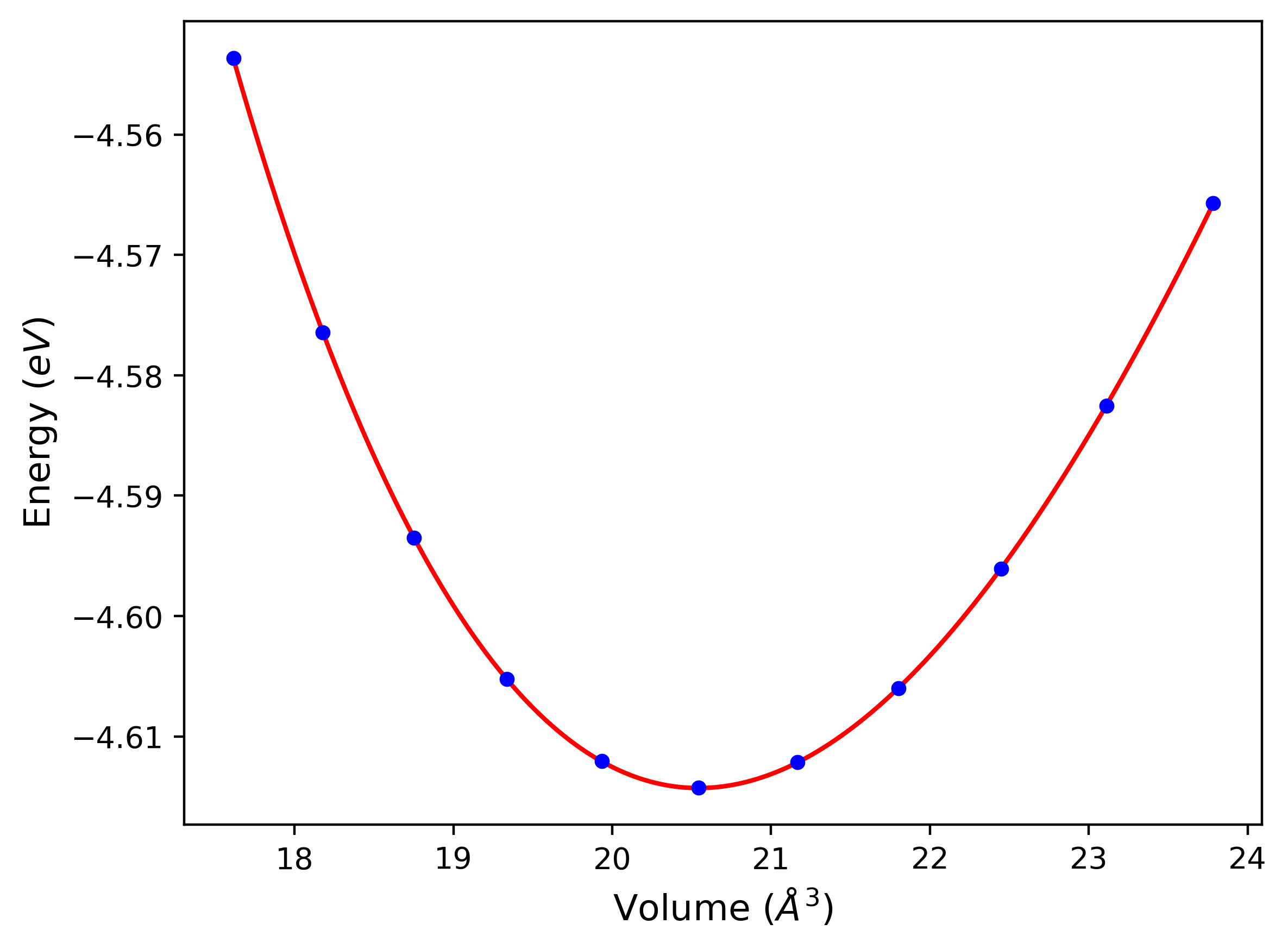
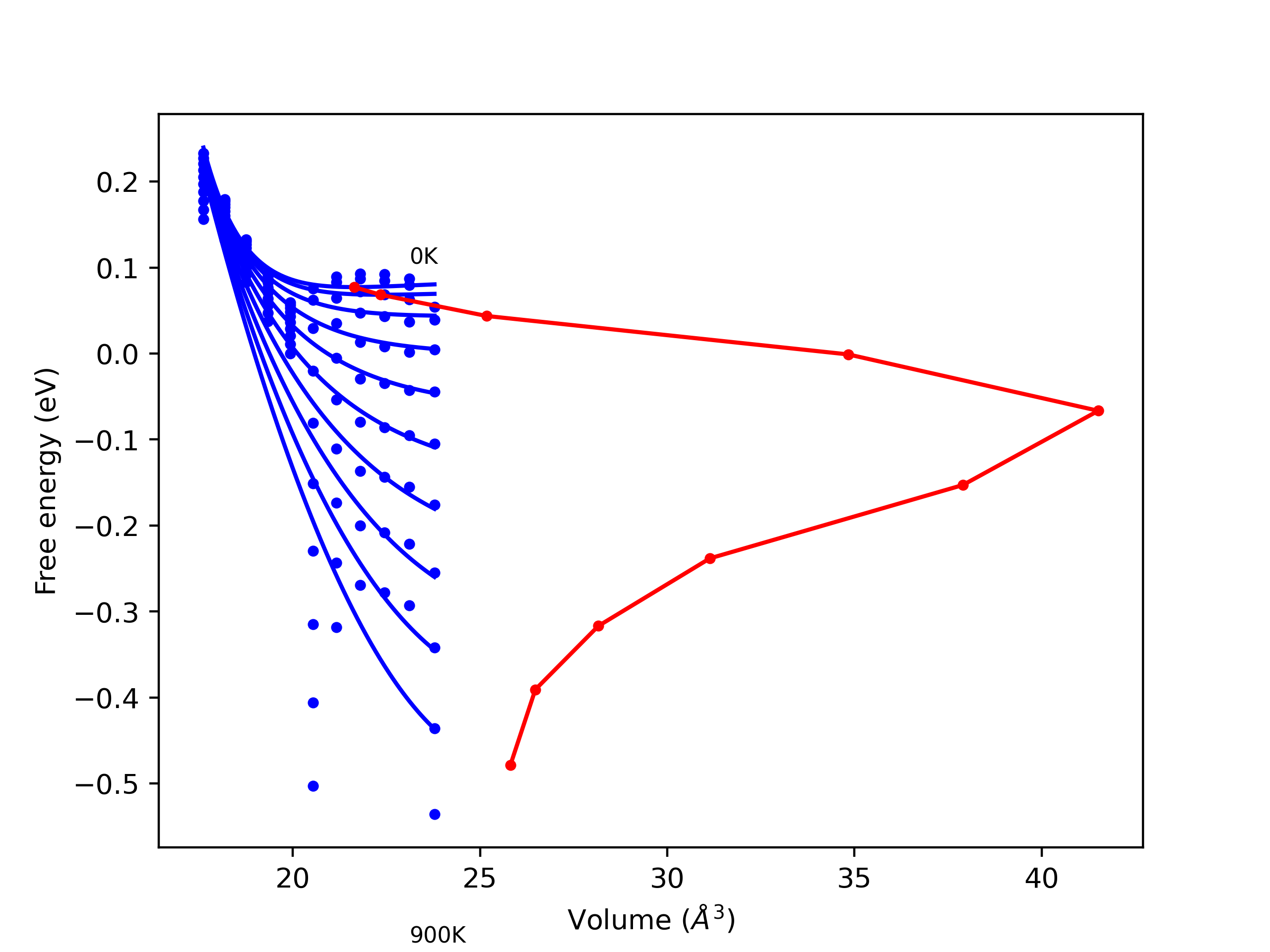
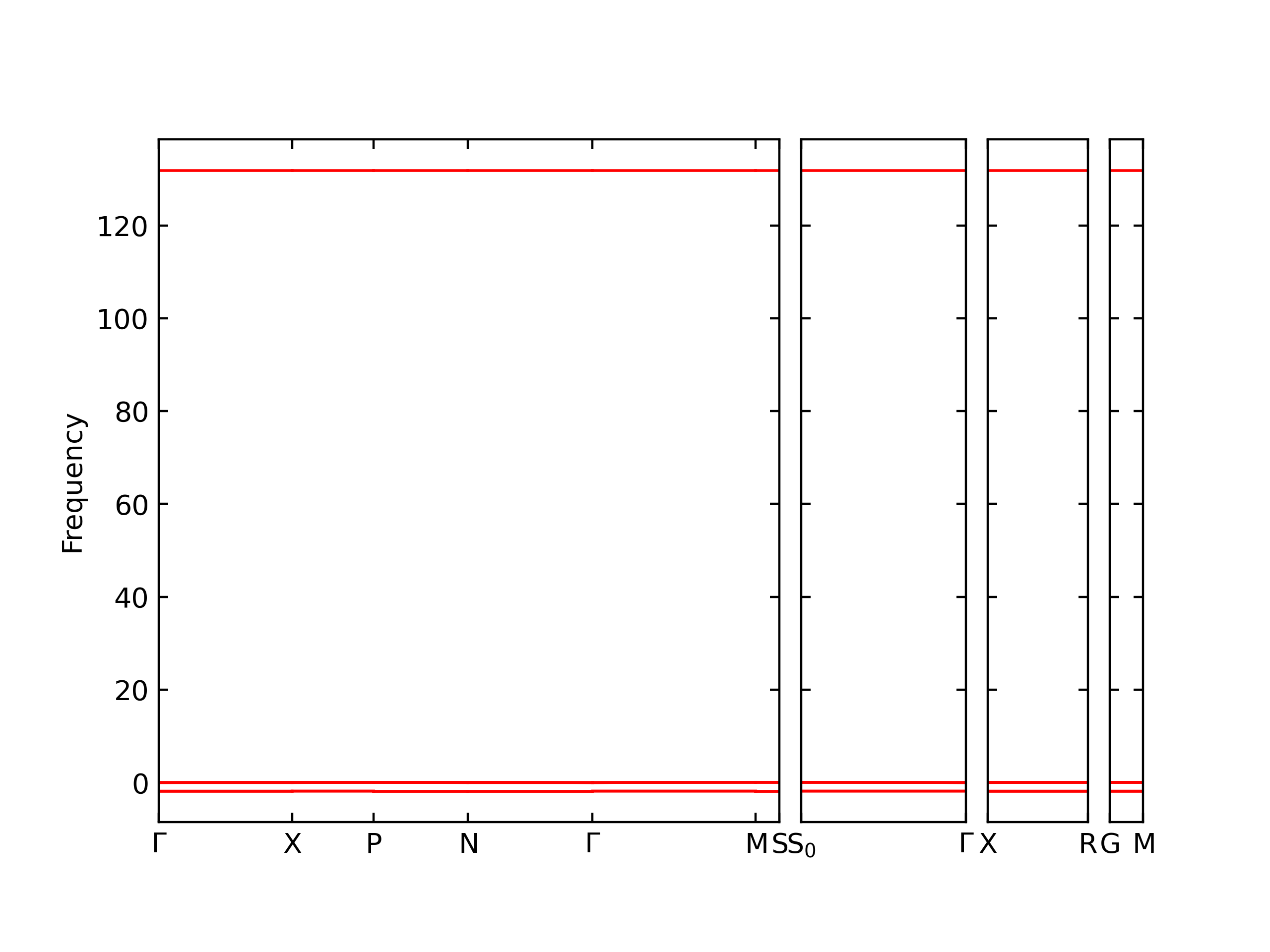
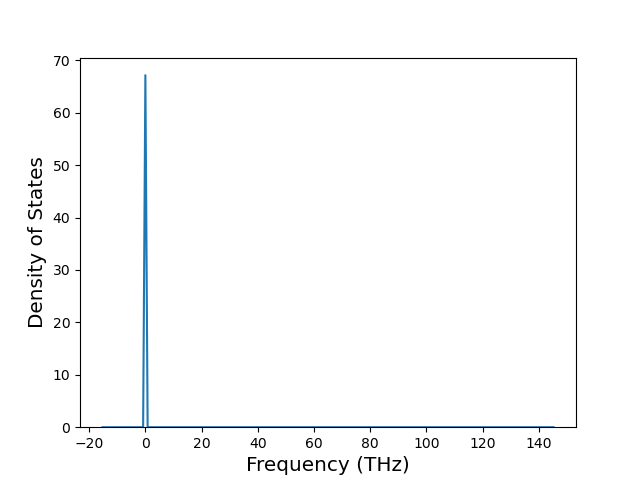
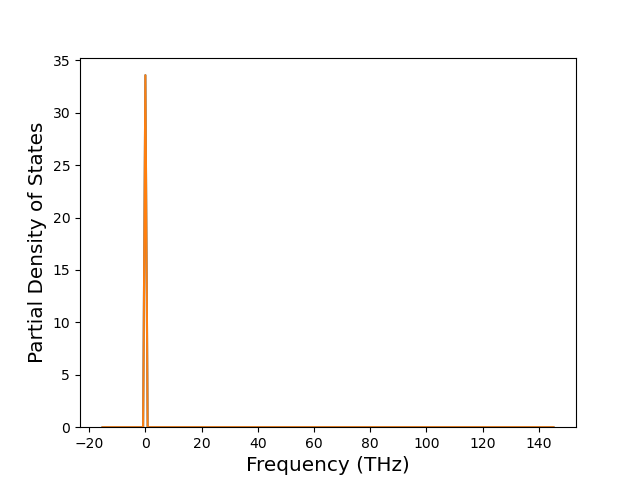
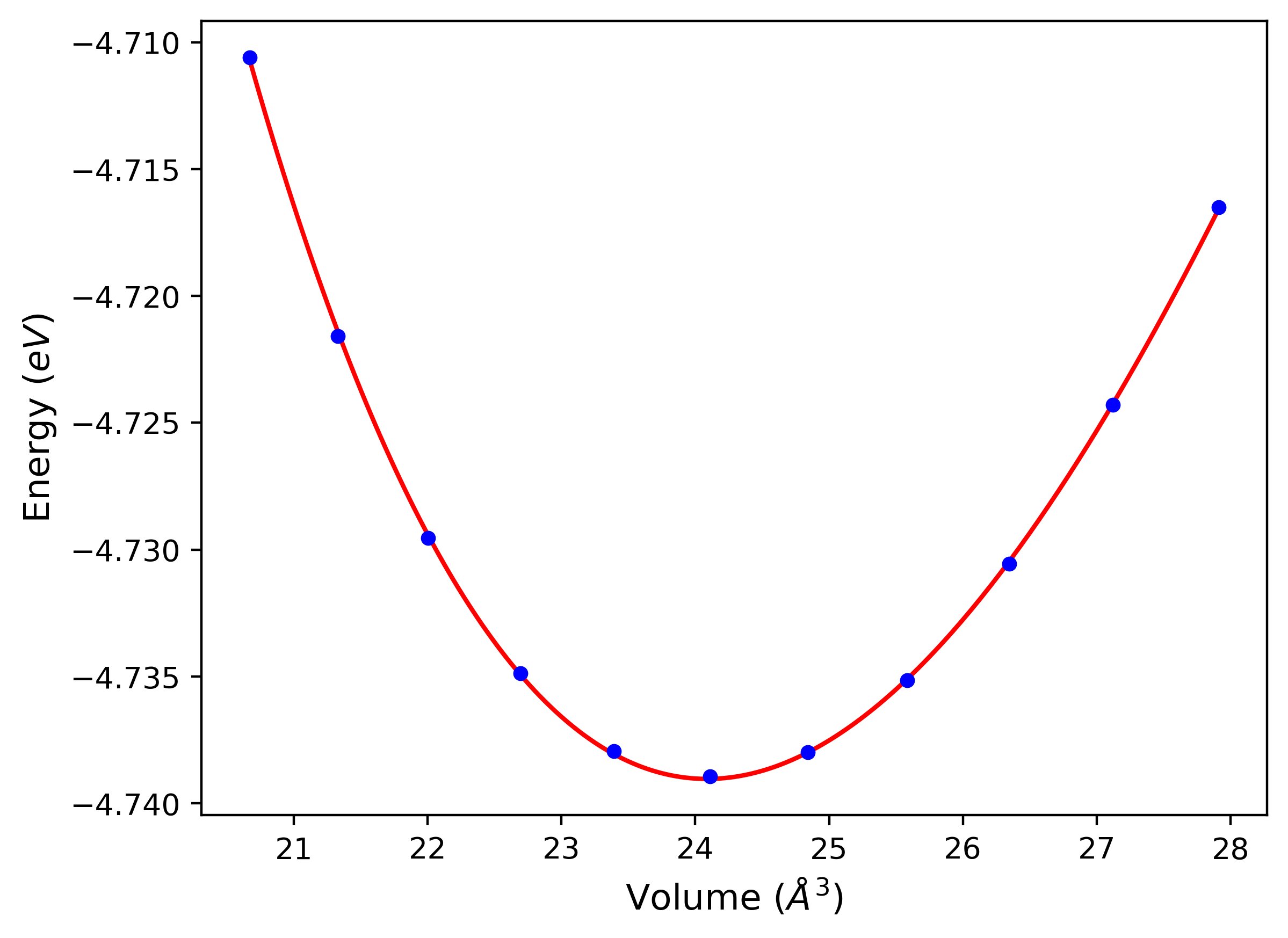
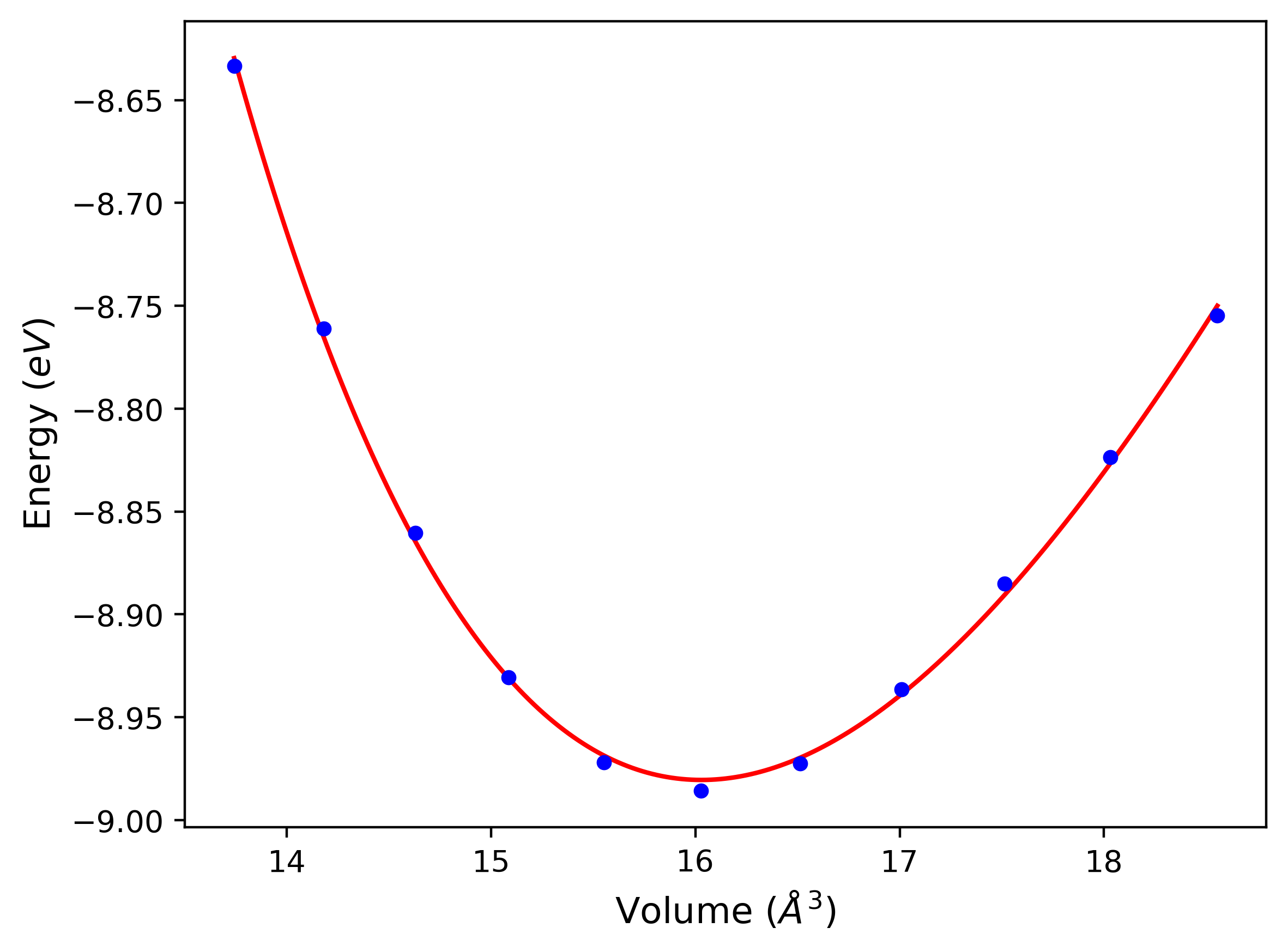
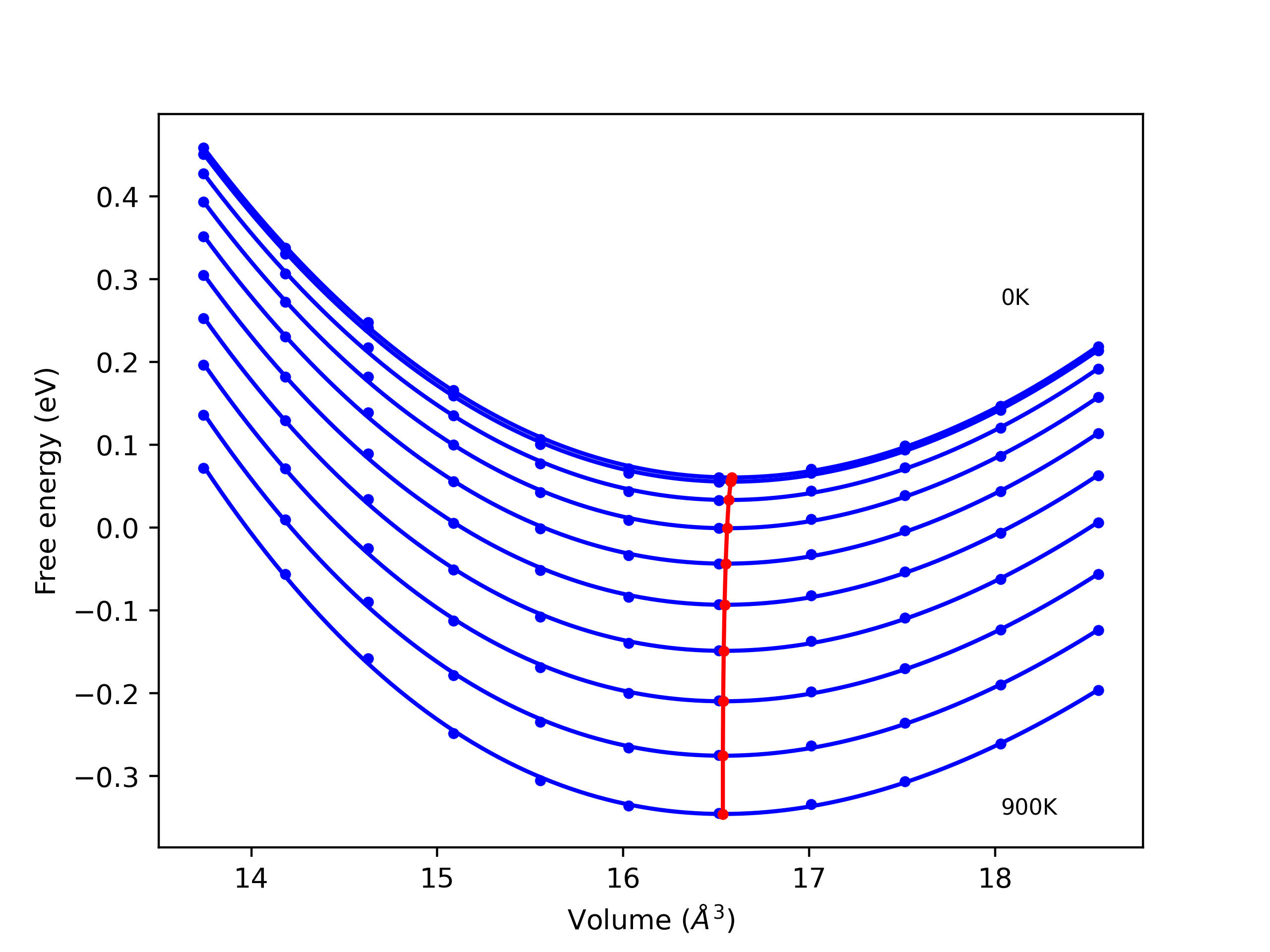
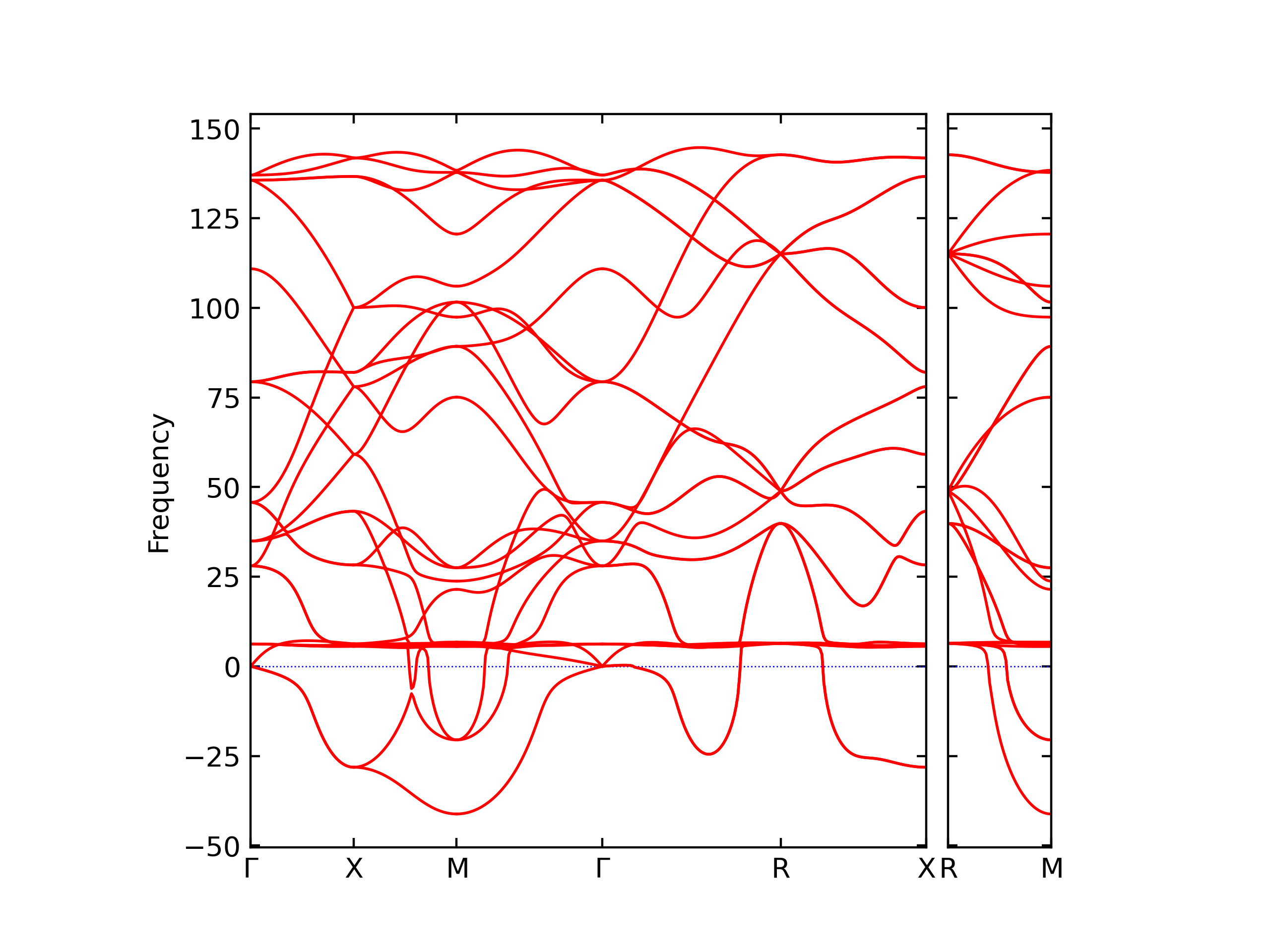
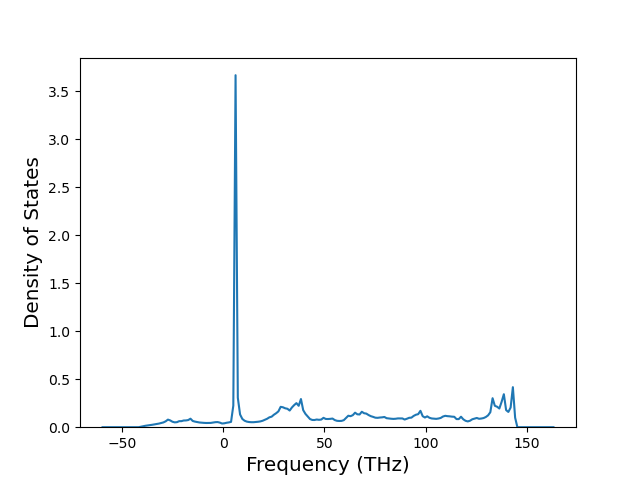
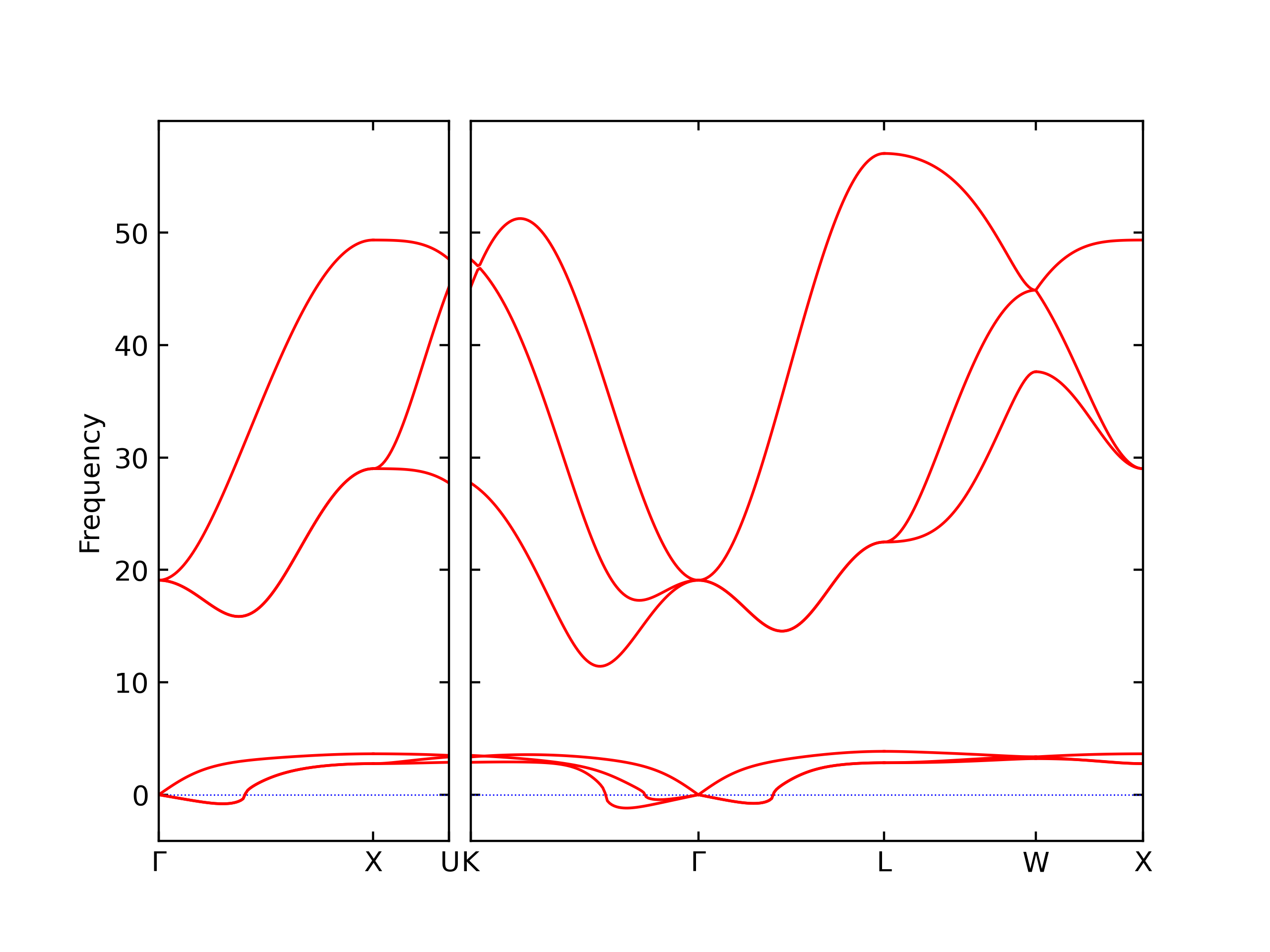
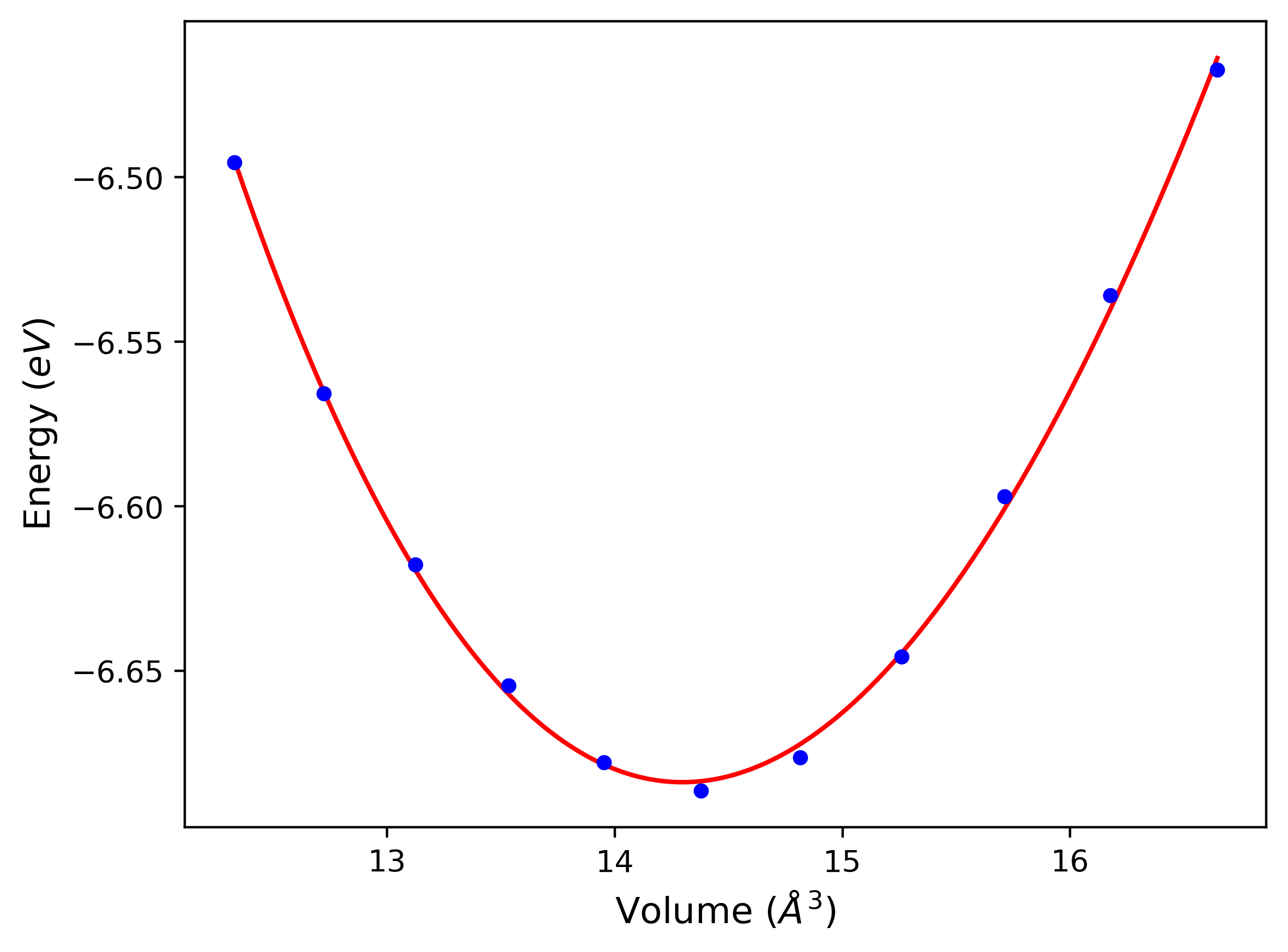
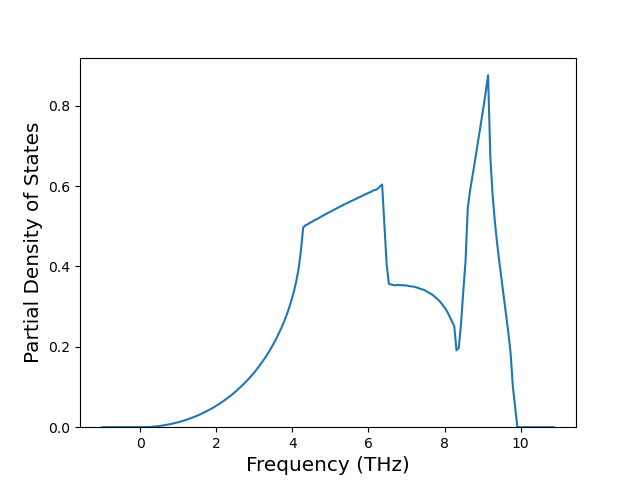
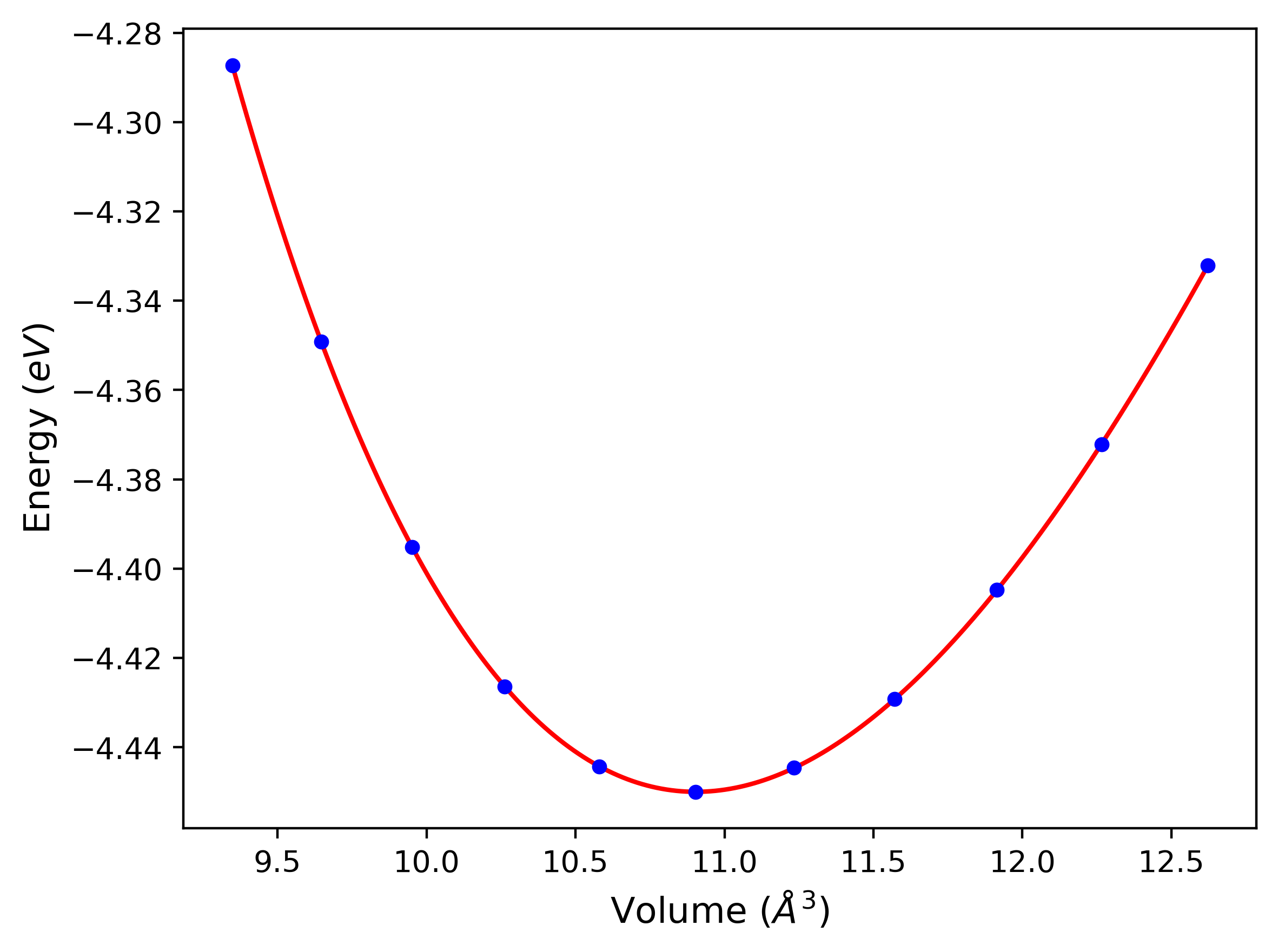
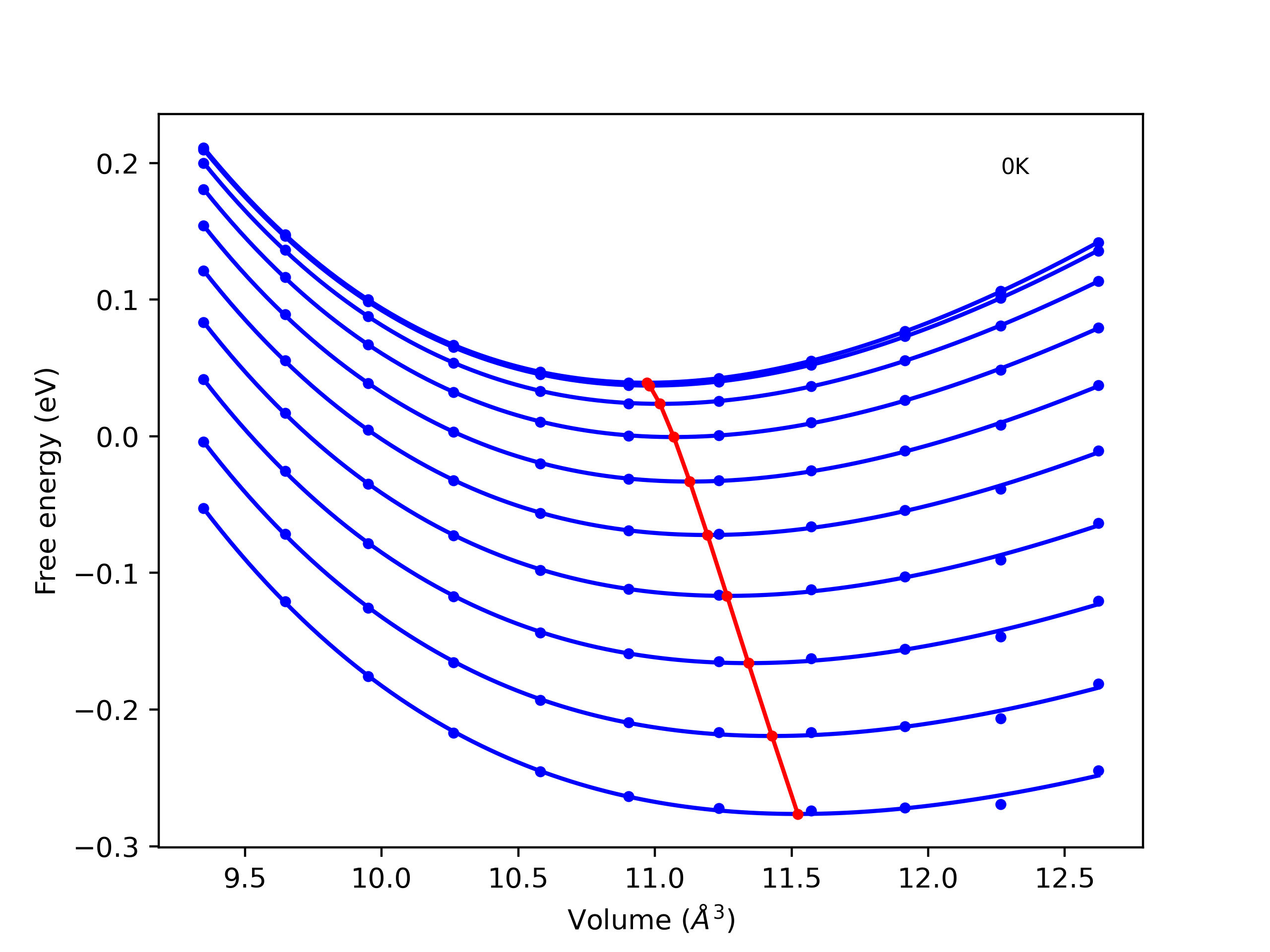
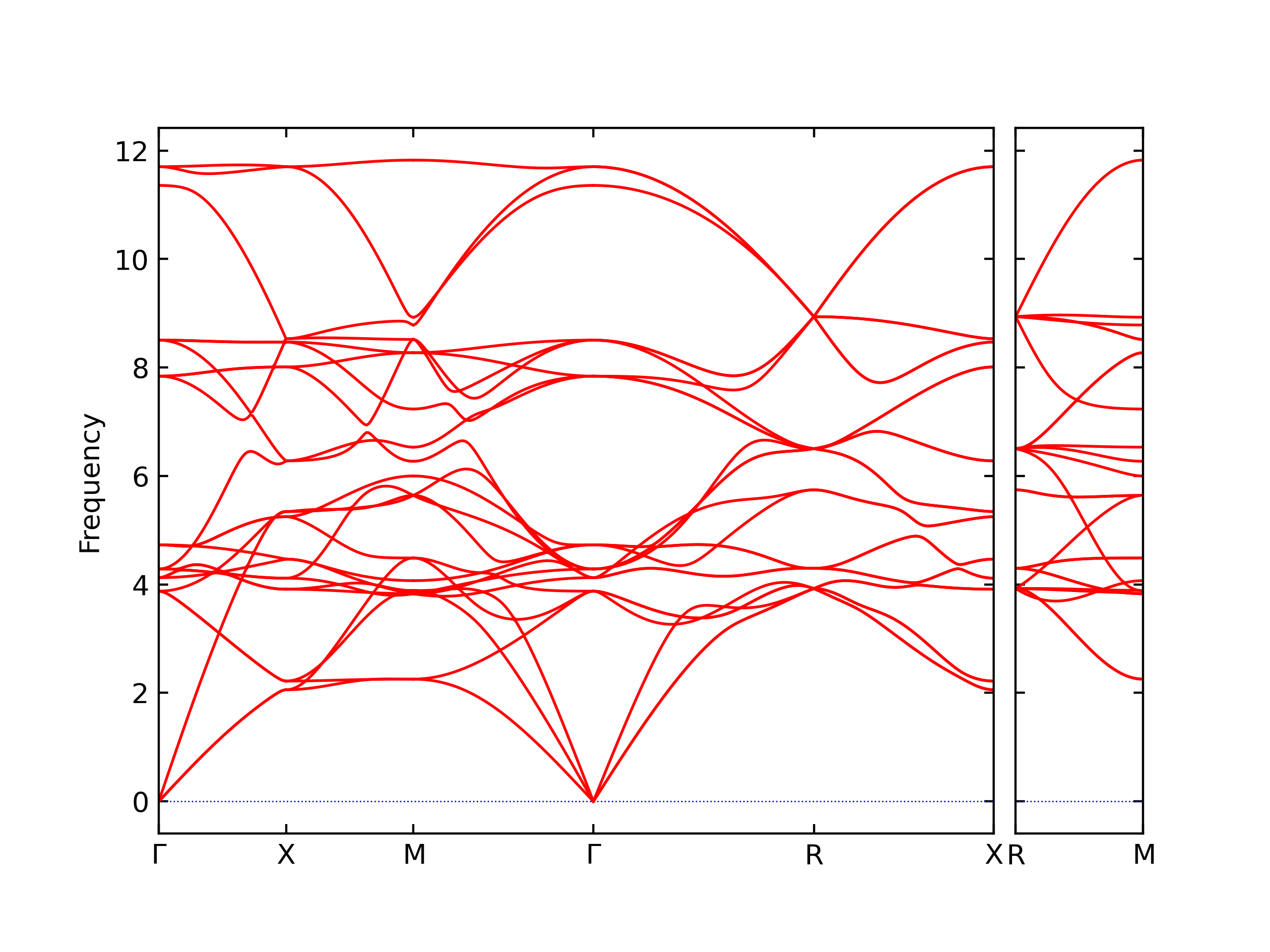
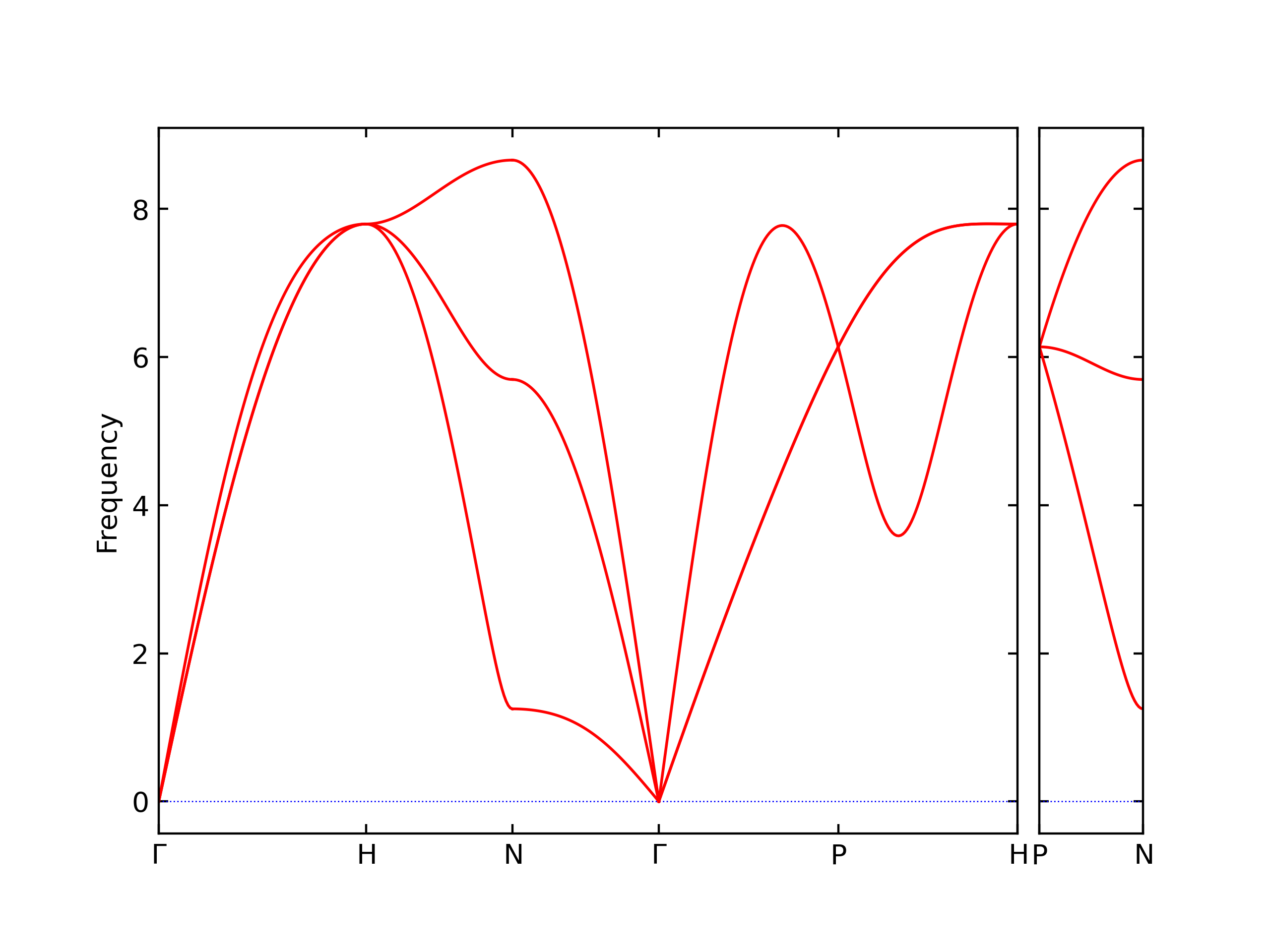
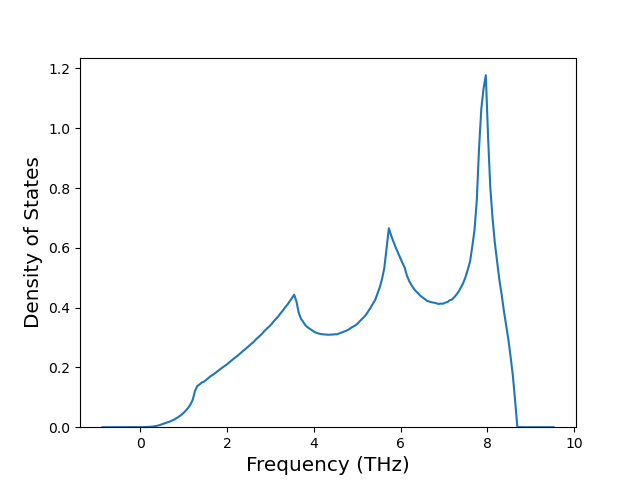
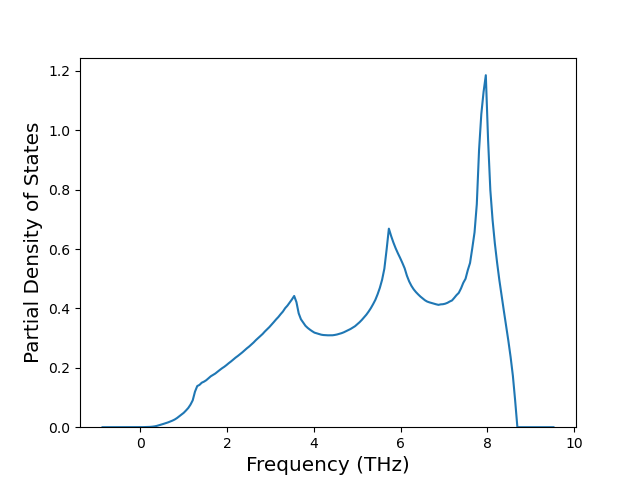
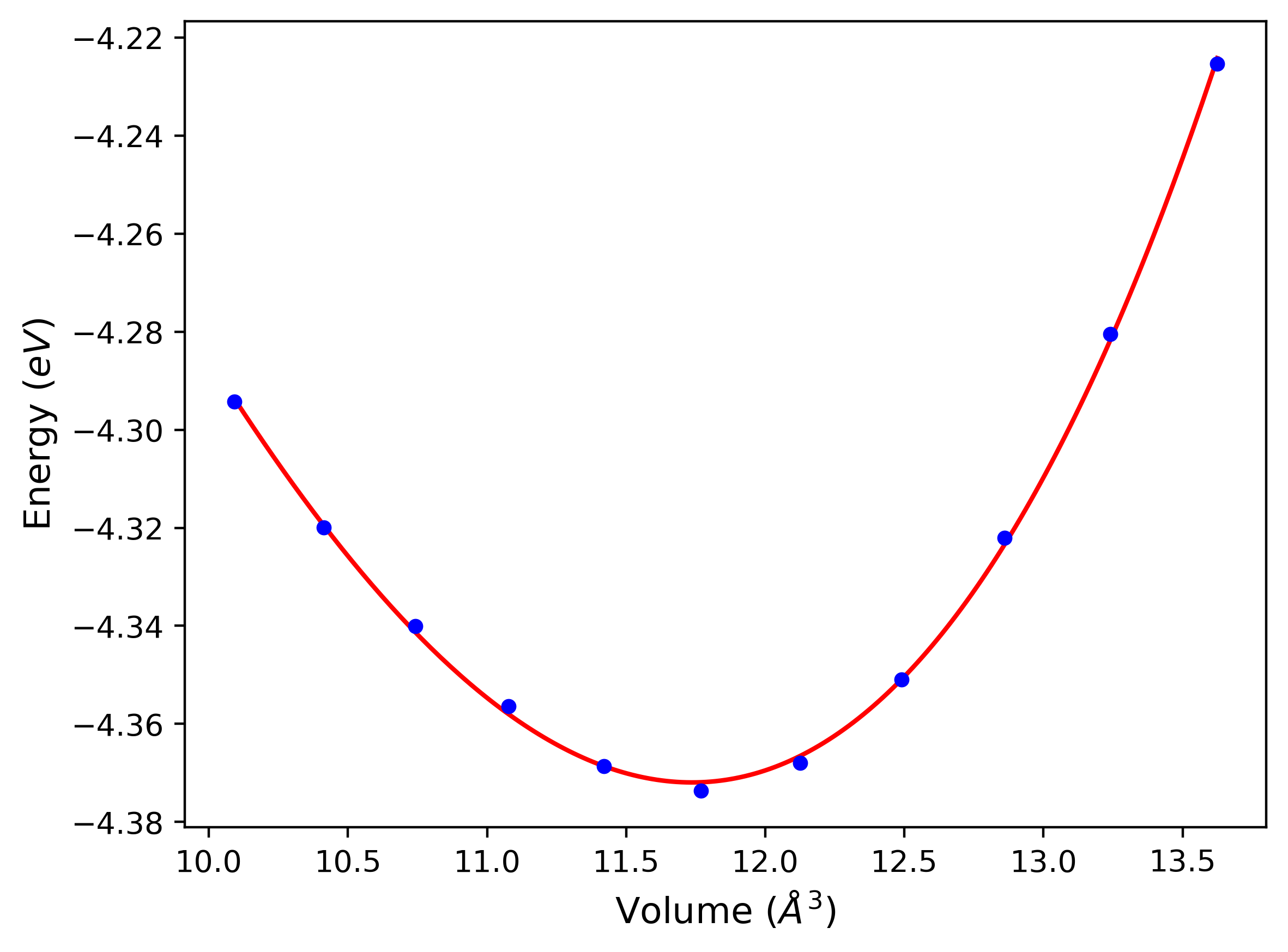
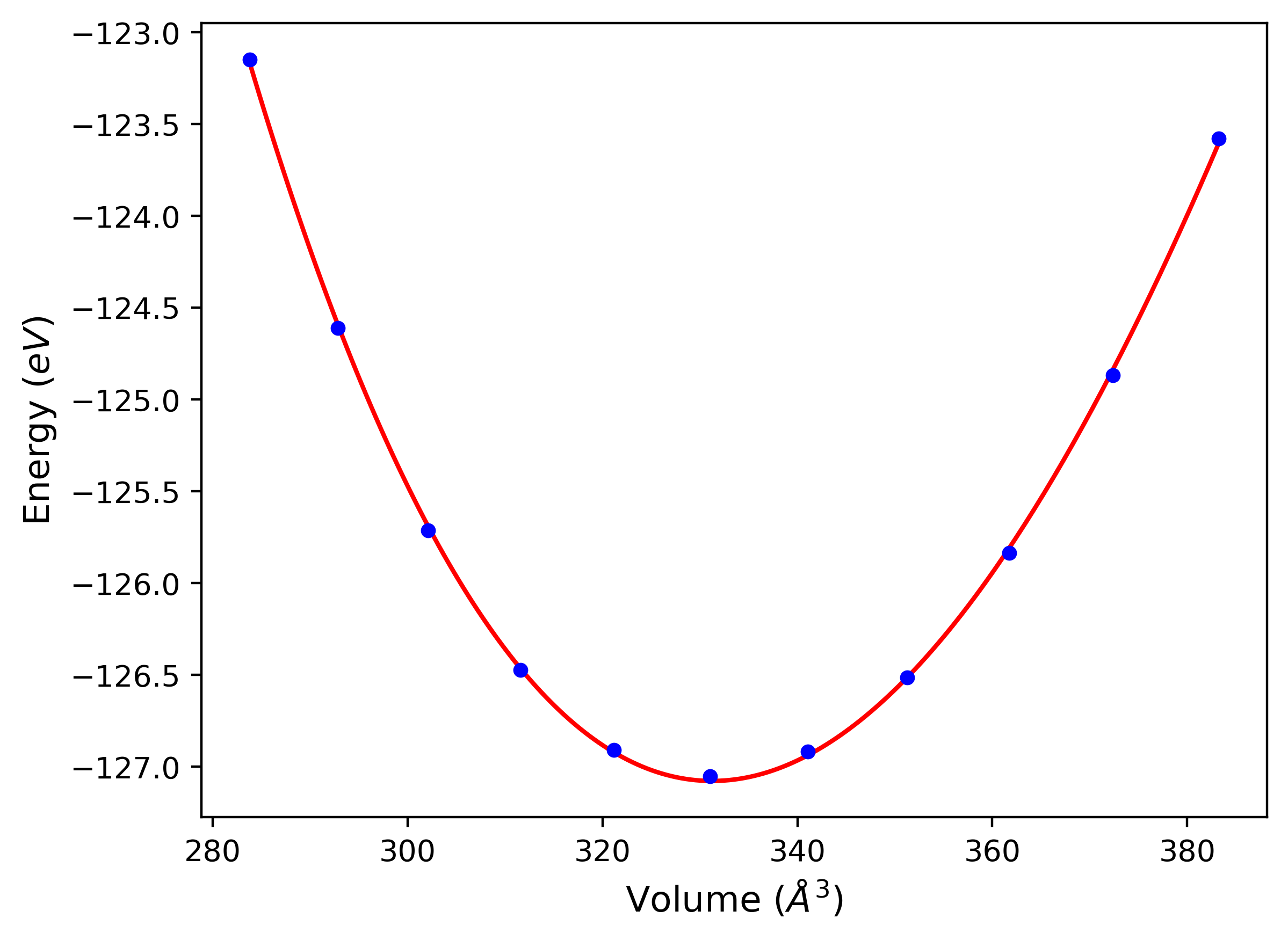
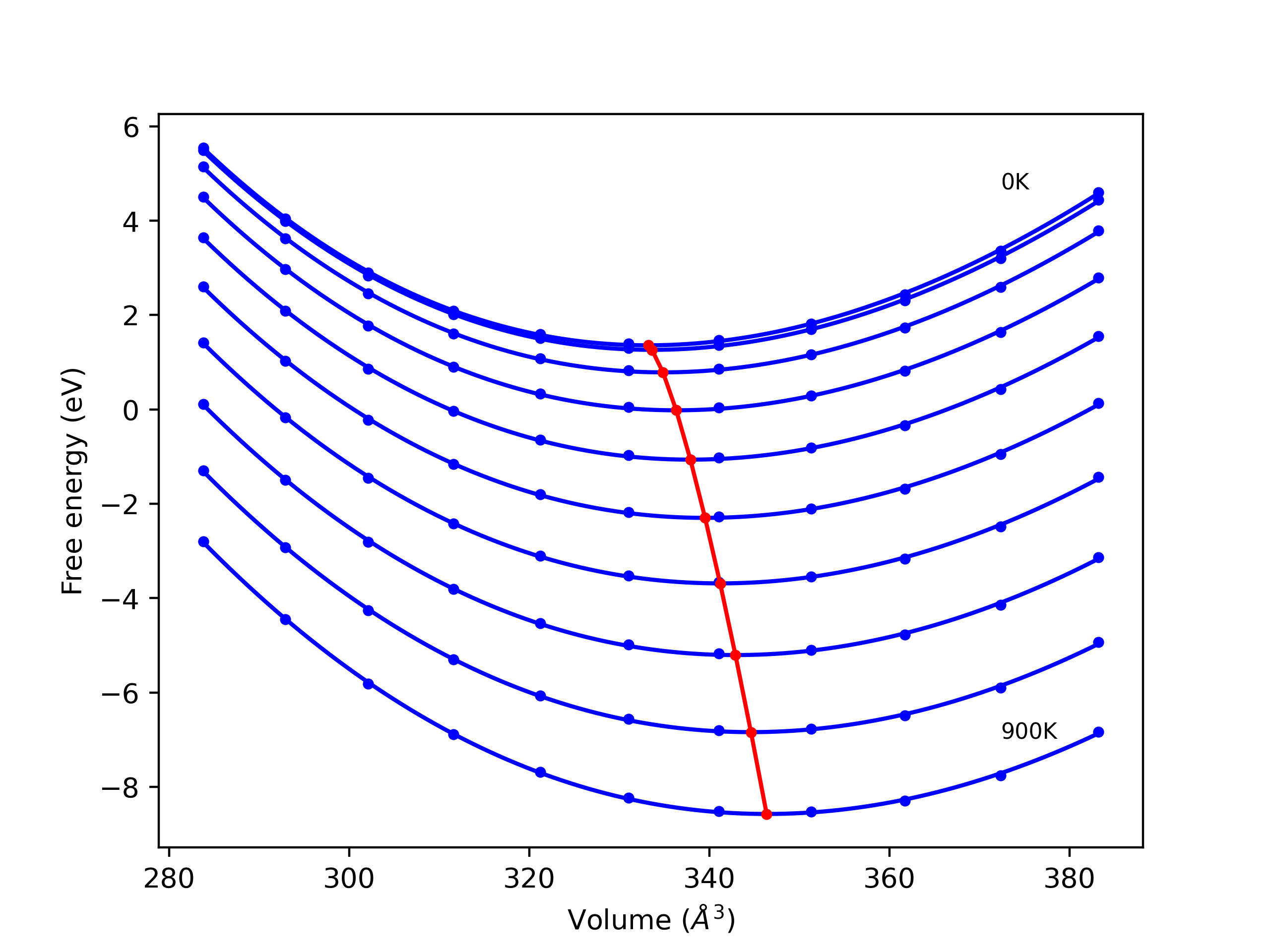
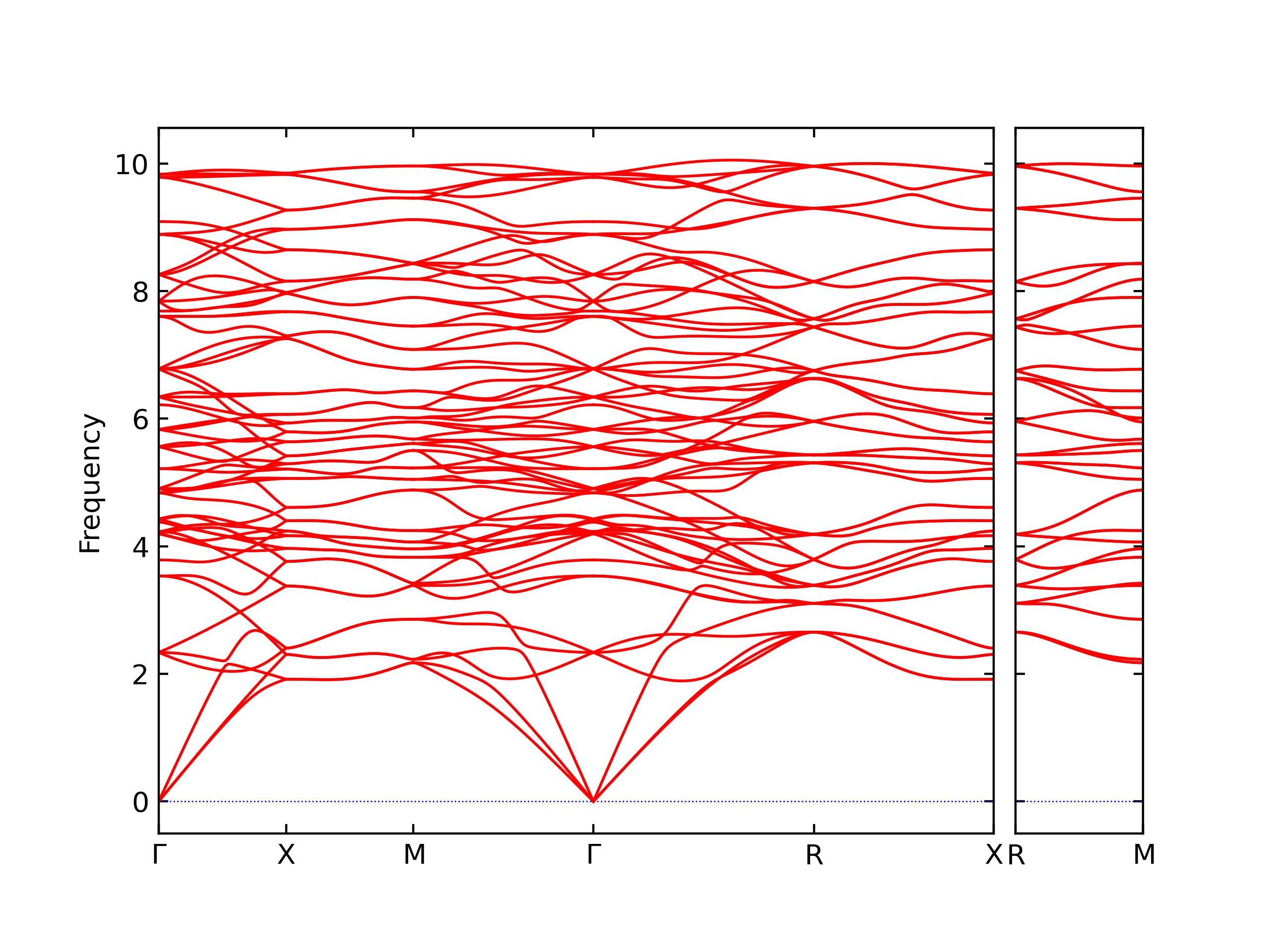
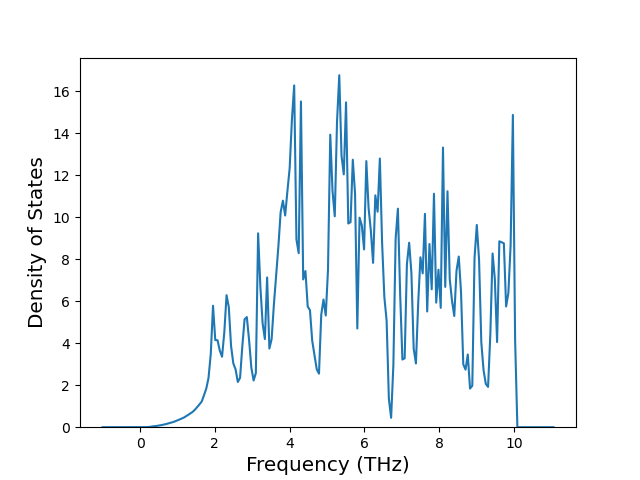
Thermodynamic Predictions
Free Surface Formation Energy Predictions
Static free surface formation energies are displayed for select crystals. The values displayed here are obtained by taking a perfect periodic bulk crystal, slicing along a crystallographic plane, and using force minimization to statically relax the surfaces. The free surface formation energy is computed by comparing the energy of the defect system to the bulk system and dividing by the total surface area created by the cut.
The calculation method used is available as the iprPy surface_energy_static calculation method.
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for variations in calculation methods, simulation software and implementations of the interatomic potentials.
- The calculation only performs straight cuts along crystallographic planes and static relaxations. Lower energy configurations may exist that require atomic restructuring of the surfaces.
- Multiple values may be listed for a given plane followed by a number indicating different unique atomic planar cuts for the same theoretical plane.
- NIST disclaimer
Version Information:
- 2019-11-14. Calculations for the alternate #2 plane slices are now different from the #1 plane slices.
- 2019-08-07. Data added.
| Surface | γfs (mJ/m2) |
|---|---|
| (111) | 1000.43 |
| (100) | 1013.77 |
| (332) | 1078.62 |
| (322) | 1084.61 |
| (221) | 1110.56 |
| (211) | 1120.50 |
| (331) | 1135.60 |
| (311) | 1138.59 |
| (110) | 1148.28 |
| (310) | 1150.51 |
| (321) | 1160.86 |
| (210) | 1178.97 |
| (320) | 1179.79 |
| Surface | γfs (mJ/m2) |
|---|---|
| (211) 2 | 1067.40 |
| (210) | 1088.27 |
| (332) 2 | 1099.51 |
| (321) 2 | 1109.17 |
| (311) | 1114.36 |
| (321) 1 | 1115.03 |
| (322) | 1117.23 |
| (221) | 1117.33 |
| (111) | 1119.92 |
| (100) | 1124.47 |
| (320) | 1131.96 |
| (331) | 1135.31 |
| (310) | 1137.56 |
| (332) 1 | 1139.04 |
| (211) 1 | 1161.39 |
| (110) | 1168.37 |
| Surface | γfs (mJ/m2) |
|---|---|
| (322) | -2329.12 |
| (331) | -2268.72 |
| (332) | -2006.79 |
| (321) | -1911.60 |
| (320) | -1803.76 |
| (310) | -1683.49 |
| (311) | -1393.04 |
| (221) | -1083.59 |
| (210) | -547.14 |
| (211) | -539.80 |
| (111) | -174.03 |
| (110) | 305.75 |
| (100) | 513.35 |
| Surface | γfs (mJ/m2) |
|---|---|
| (0001) | 970.95 |
| (1012) 2 | 1021.58 |
| (1011) 1 | 1067.26 |
| (2021) 1 | 1067.70 |
| (2021) 2 | 1120.54 |
| (1011) 2 | 1156.48 |
| (1120) | 1159.63 |
| (1010) | 1160.85 |
| (2131) 1 | 1166.48 |
| (1012) 1 | 1170.00 |
| (2132) 2 | 1170.46 |
| (2241) | 1174.88 |
| (2132) 1 | 1176.73 |
| (1121) | 1185.33 |
| (2112) | 1192.77 |
| (2130) | 1193.50 |
| (2131) 2 | 1203.47 |
| Surface | γfs (mJ/m2) |
|---|---|
| (0001) | 983.67 |
| (1011) 1 | 1046.71 |
| (1011) 2 | 1046.71 |
| (1010) 1 | 1066.54 |
| (2021) 1 | 1077.19 |
| (1012) 1 | 1114.73 |
| (1012) 2 | 1168.54 |
| (2130) 1 | 1169.54 |
| (2112) | 1172.90 |
| (2021) 2 | 1178.94 |
| (1120) | 1180.02 |
| (2132) 2 | 1180.88 |
| (2132) 1 | 1180.96 |
| (2131) 2 | 1189.64 |
| (2131) 1 | 1198.75 |
| (2241) | 1202.72 |
| (1121) | 1214.41 |
| (2130) 2 | 1246.82 |
| (1010) 2 | 1271.86 |
| Surface | γfs (mJ/m2) |
|---|---|
| (111) | 1929.07 |
| (100) | 2059.99 |
| (332) | 2133.58 |
| (322) | 2153.65 |
| (221) | 2223.96 |
| (211) | 2263.35 |
| (331) | 2299.45 |
| (311) | 2340.02 |
| (110) | 2351.73 |
| (321) | 2369.86 |
| (310) | 2371.84 |
| (320) | 2427.76 |
| (210) | 2430.84 |
| Surface | γfs (mJ/m2) |
|---|---|
| (211) 2 | 1999.94 |
| (210) | 2057.03 |
| (332) 2 | 2092.87 |
| (321) 2 | 2108.97 |
| (311) | 2120.40 |
| (321) 1 | 2125.16 |
| (100) | 2127.77 |
| (111) | 2132.16 |
| (221) | 2138.54 |
| (322) | 2146.91 |
| (310) | 2168.82 |
| (332) 1 | 2172.82 |
| (331) | 2178.71 |
| (320) | 2182.83 |
| (211) 1 | 2251.03 |
| (110) | 2258.94 |
| Surface | γfs (mJ/m2) |
|---|---|
| (321) | -1339.28 |
| (331) | -1200.80 |
| (320) | -959.25 |
| (322) | -457.99 |
| (211) | 25.14 |
| (210) | 315.67 |
| (311) | 564.90 |
| (221) | 891.12 |
| (332) | 1648.98 |
| (310) | 1767.70 |
| (110) | 1977.71 |
| (100) | 2271.56 |
| (111) | 2350.41 |
Stacking Fault Energy Predictions
Stacking fault energy plots and maps are displayed for select crystals. The values are computed by
- Starting with a bulk crystal system
- Creating a free surface along one of the system's periodic boundaries and using force minimization to relax it
- The system is sliced in half along a crystallographic plane parallel to the free surface. One half of the system is shifted relative to the other
- The atoms in the shifted system are allowed to relax only in the direction normal to the shifting plane
- The stacking fault energy for a given shift is computed by comparing the energy of the system before and after applying the shift, and dividing by the area of the fault plane
The calculation method used is available as the iprPy stacking_fault_map_2D calculation method.
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for variations in calculation methods, simulation software and implementations of the interatomic potentials.
- Values between the measured points are interpolated and therefore may not perfectly capture minima and maxima.
- Multiple values may be listed for a given plane followed by a number indicating different unique atomic planar cuts for the same theoretical plane.
- NIST disclaimer
Version Information:
- 2022-06-28. Table added for intrinsic and unstable energies, and ideal shear stresses. Plots (and table) now ordered by the associated planes.
- 2019-11-14. Calculations for the alternate #2 plane slices are now different from the #1 plane slices. The 1D plotting vectors have been changed to avoid duplicates. Minor improvements to how the 2D plots are displayed.
- 2019-08-07. Plots added.
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [0 -1 1] | 97.33 |
| τ_ideal a/2 [0 -1 1] | 2.74 |
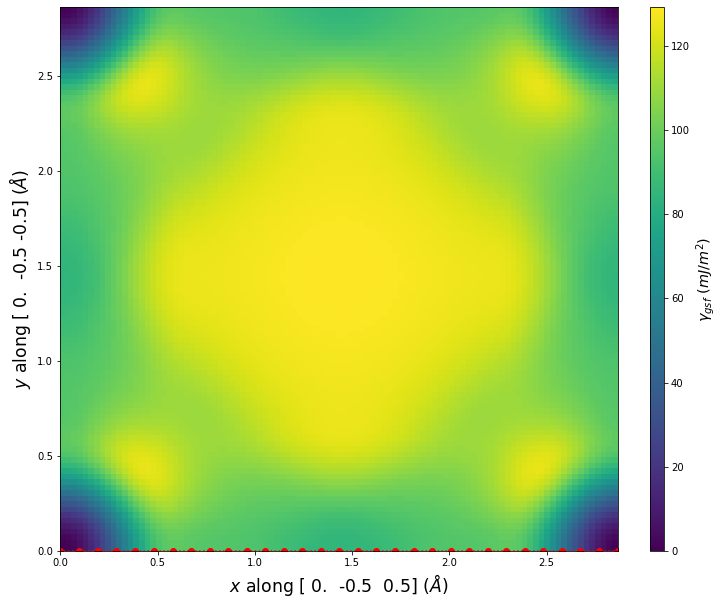
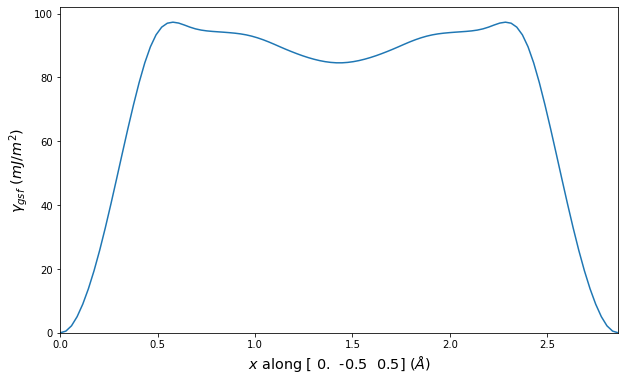
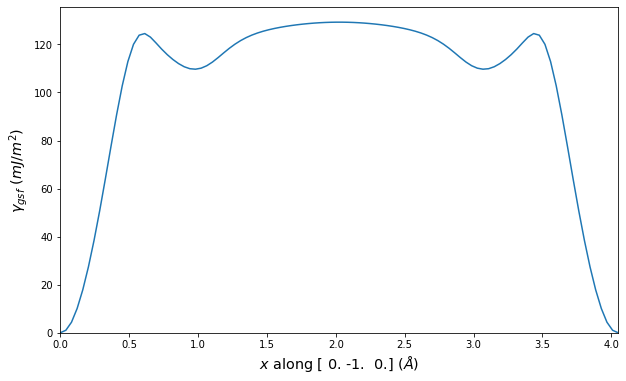
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_isf | 98.87 |
| E_usf a/2 [0 -1 1] | 115.25 |
| τ_ideal a/2 [0 -1 1] | 1.82 |
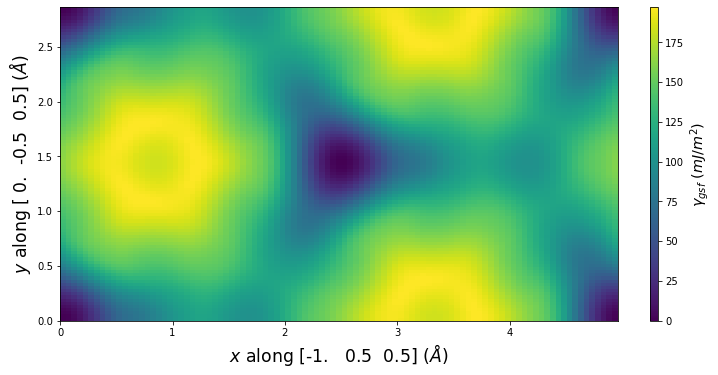
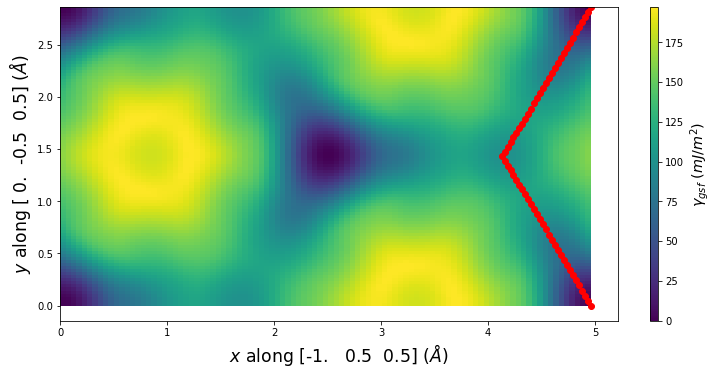
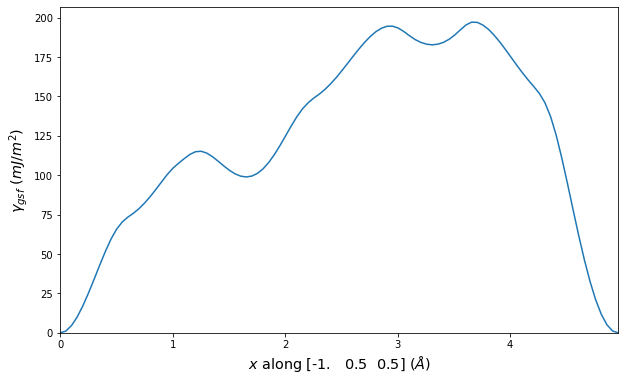
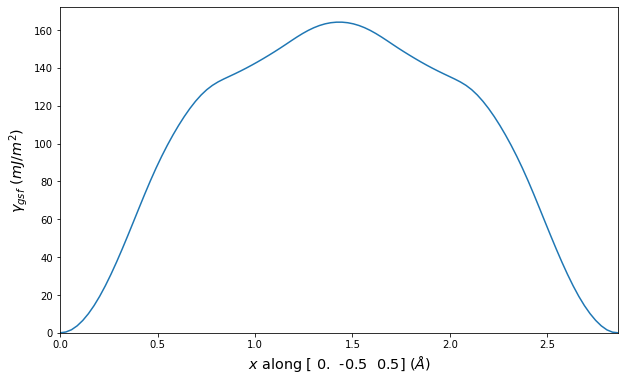
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [-1 1 -1] | 392.74 |
| τ_ideal a/2 [-1 1 -1] | 241.70 |
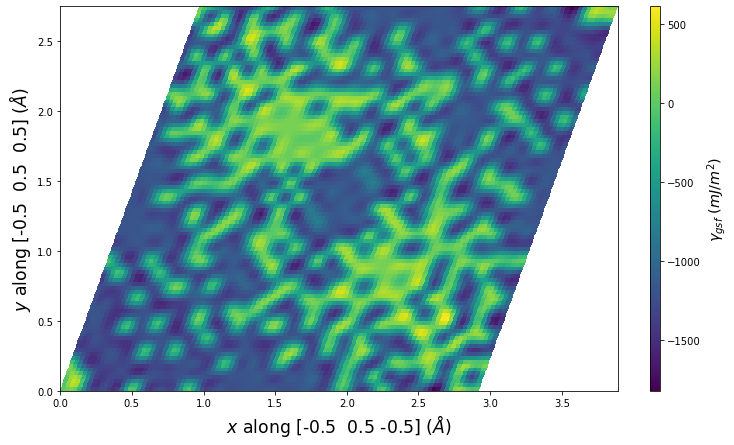
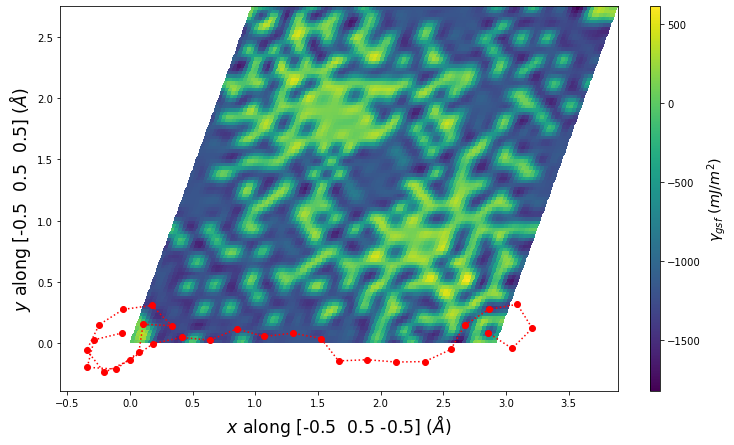
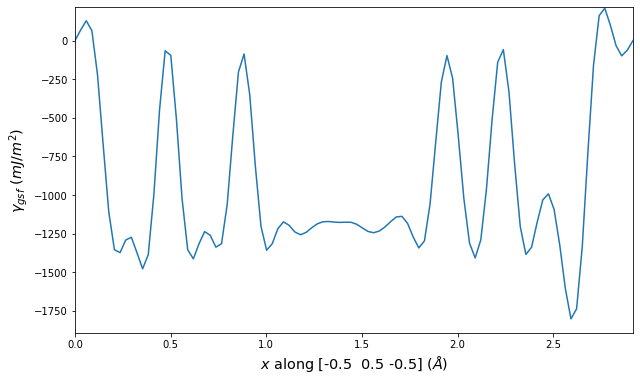
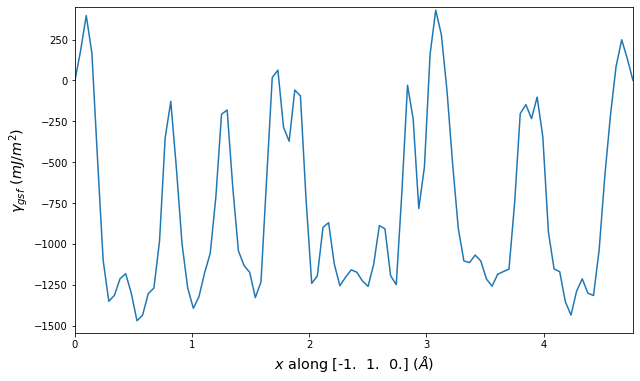
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [-1 -1 1] | 662.18 |
| τ_ideal a/2 [-1 -1 1] | 73.06 |
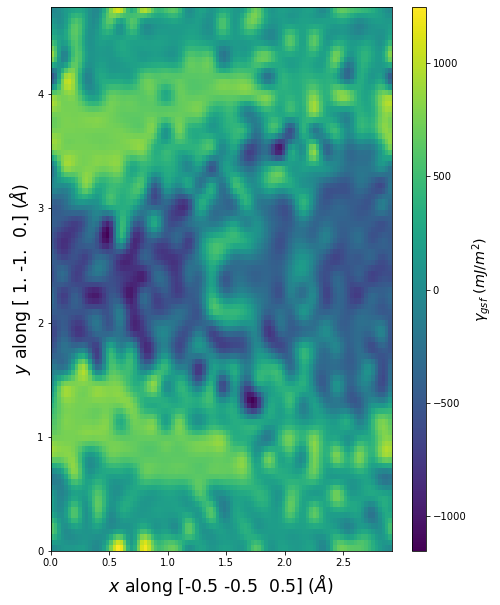
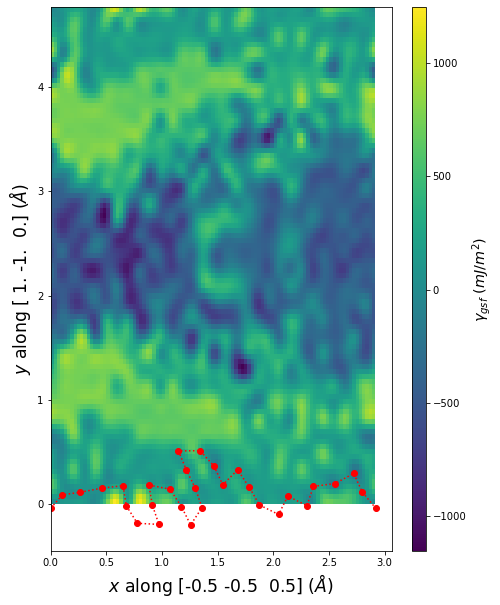
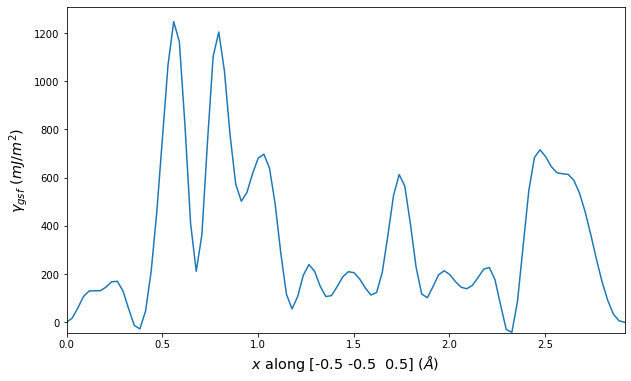
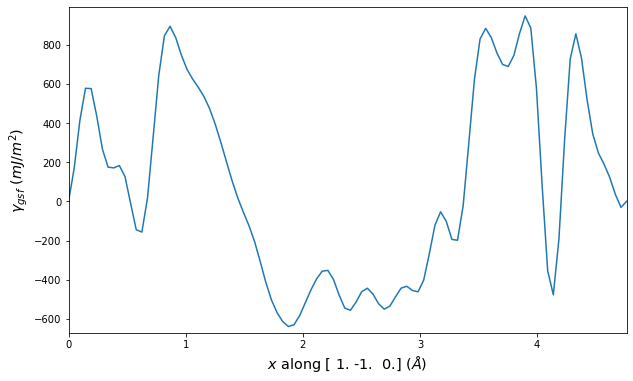
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [-1 -1 1] | 301.41 |
| τ_ideal a/2 [-1 -1 1] | 174.13 |

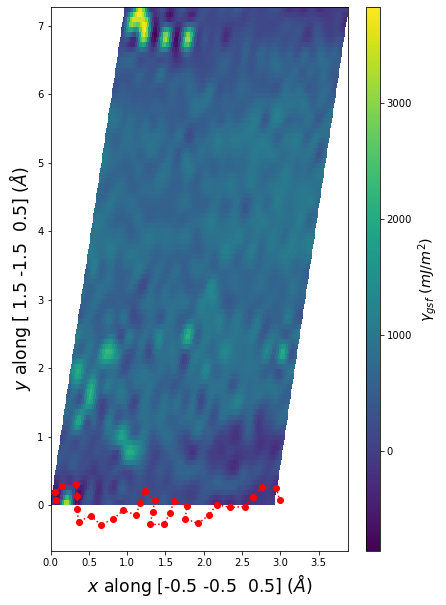
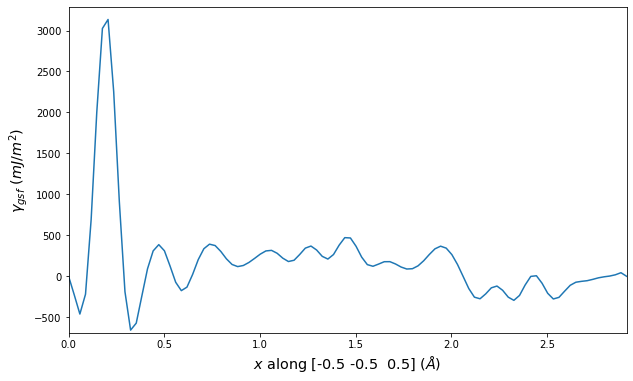
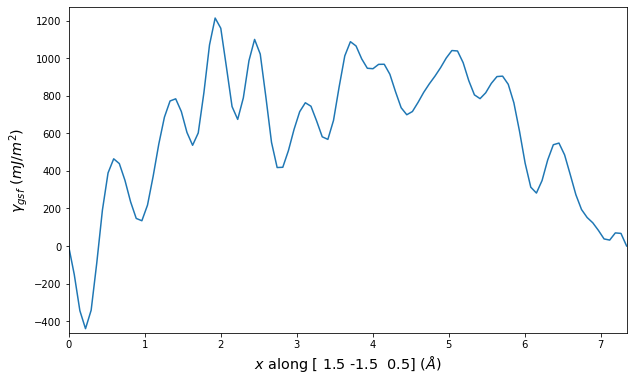
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_isf | -12.02 |
| E_usf a/3 [-2 1 1 0] | 52.56 |
| τ_ideal a/3 [-2 1 1 0] | 1.74 |
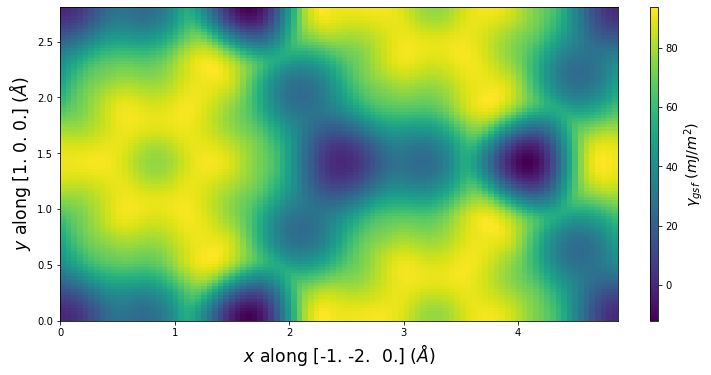
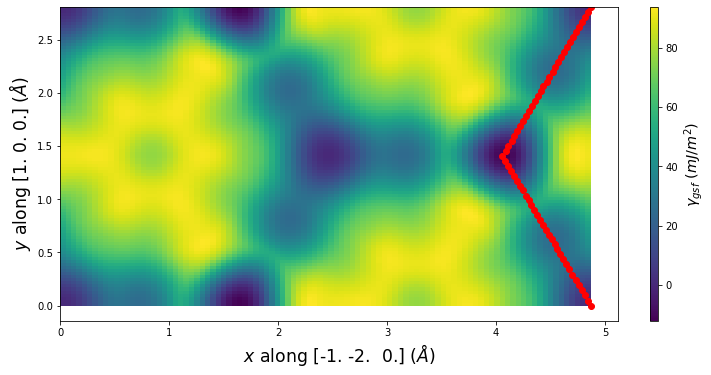
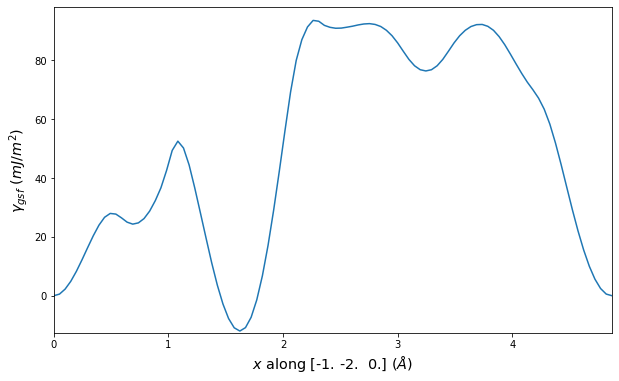
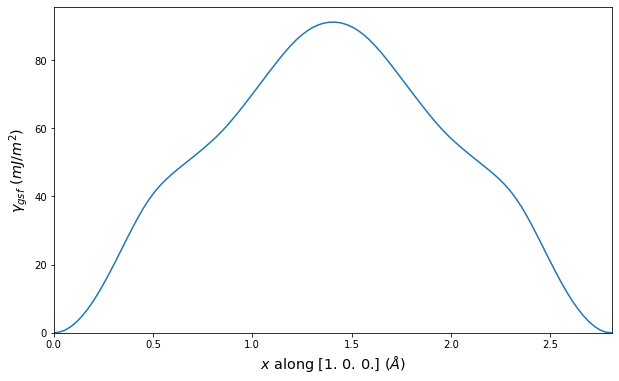
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/3 [-1 2 -1 0] | 96.85 |
| τ_ideal a/3 [-1 2 -1 0] | 16.74 |
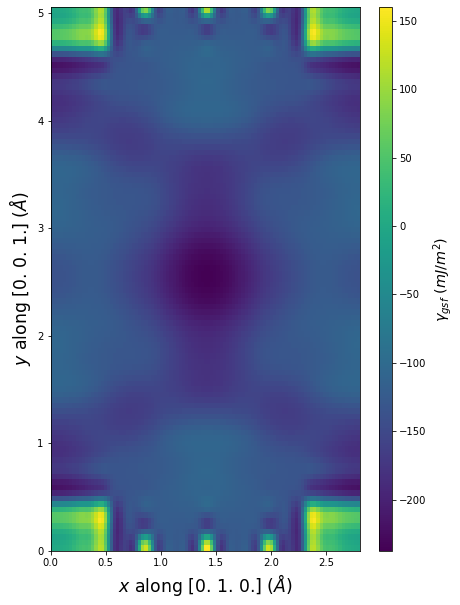
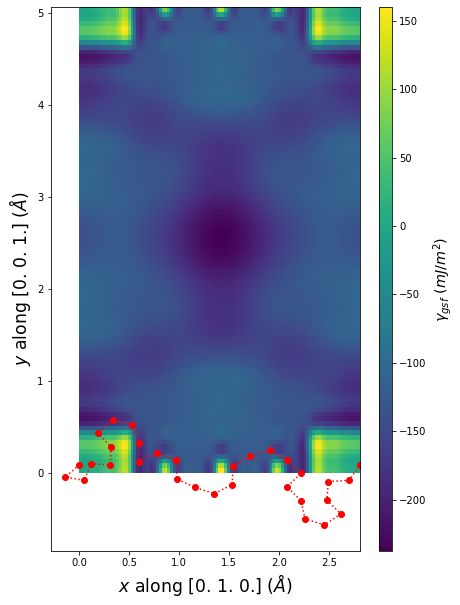
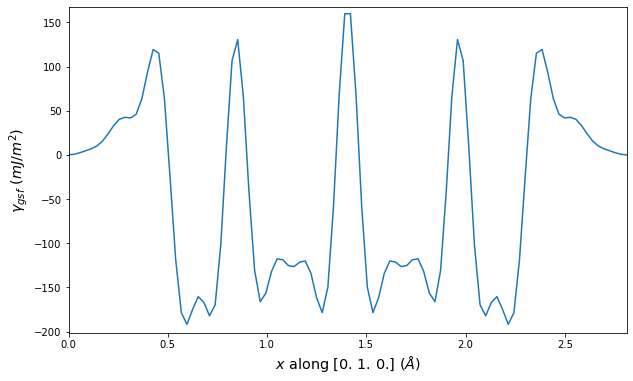
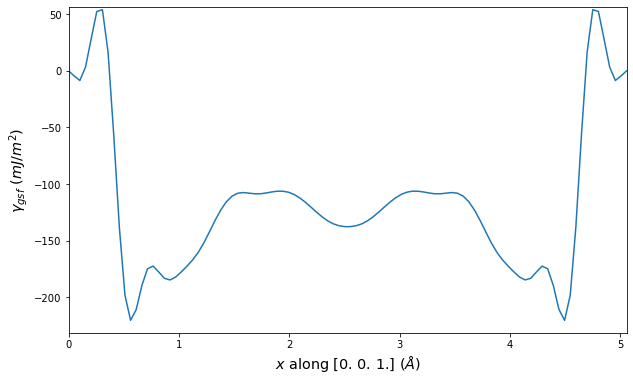
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/3 [-1 2 -1 0] | 77.99 |
| τ_ideal a/3 [-1 2 -1 0] | 2.35 |
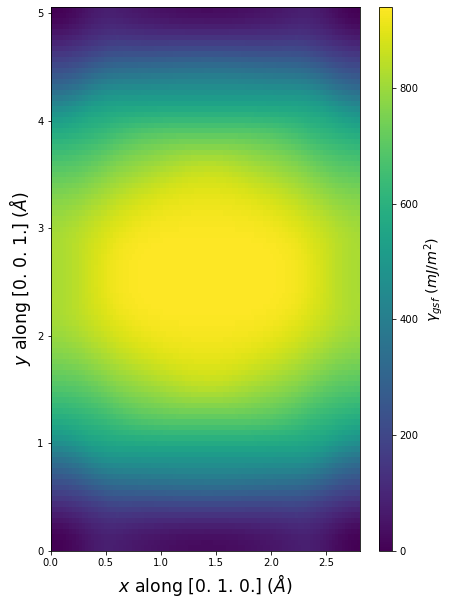
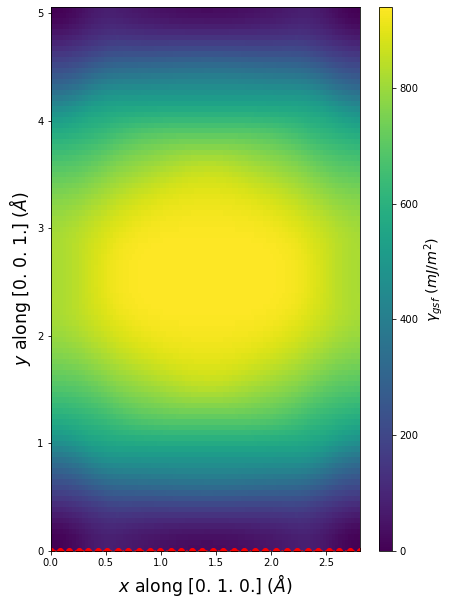
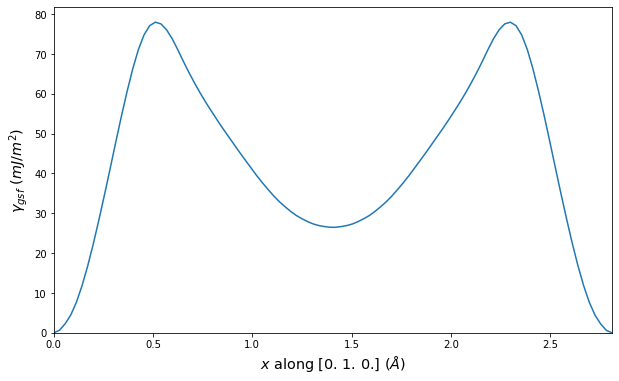
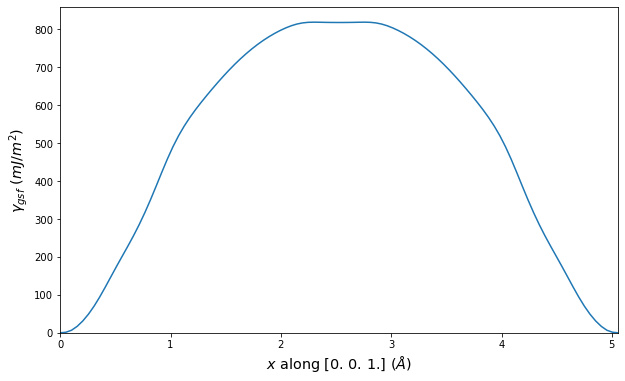
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/3 [-1 2 -1 0] | 232.88 |
| E_usf a/3 [-2 1 1 3] | 1633.36 |
| τ_ideal a/3 [-1 2 -1 0] | 3.16 |
| τ_ideal a/3 [-2 1 1 3] | 12.13 |
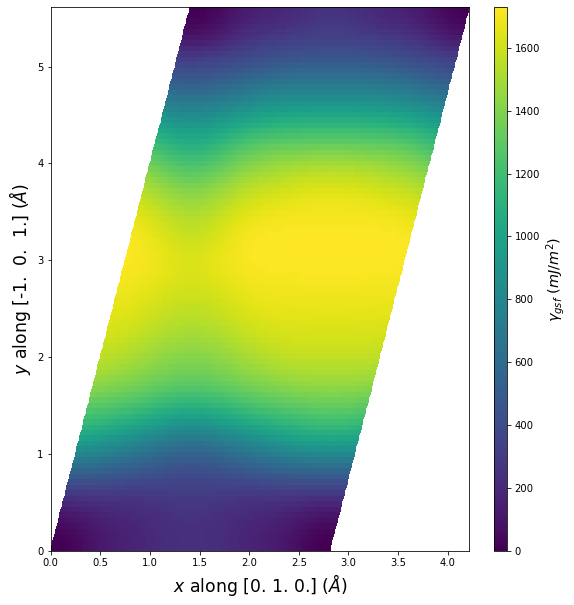
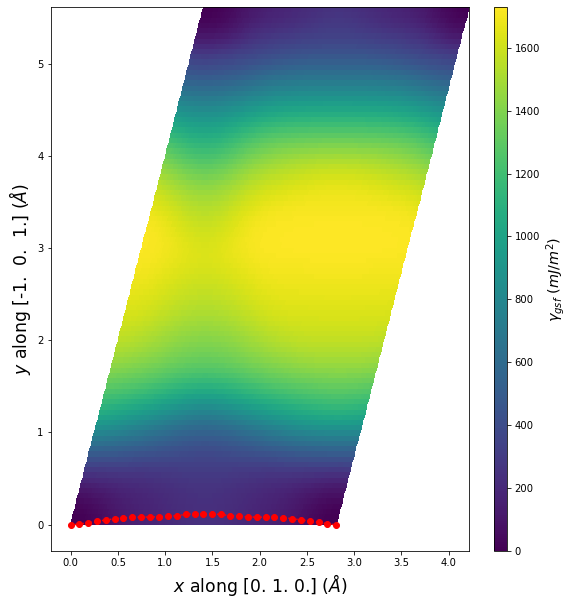
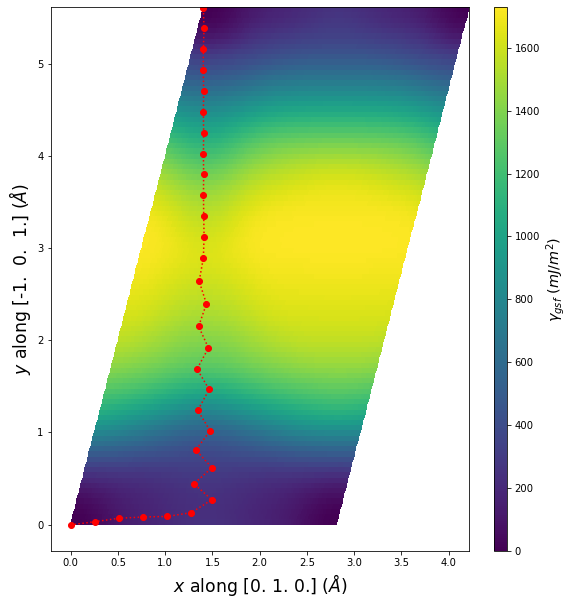
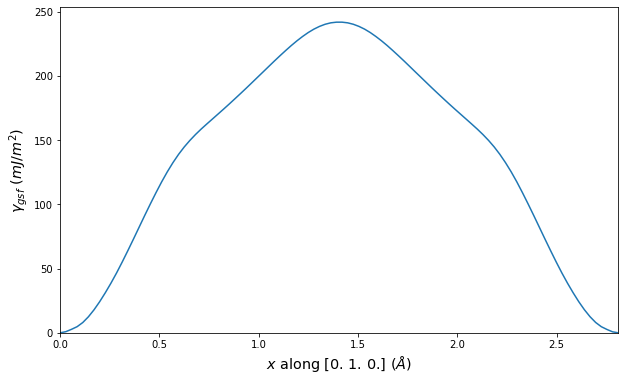
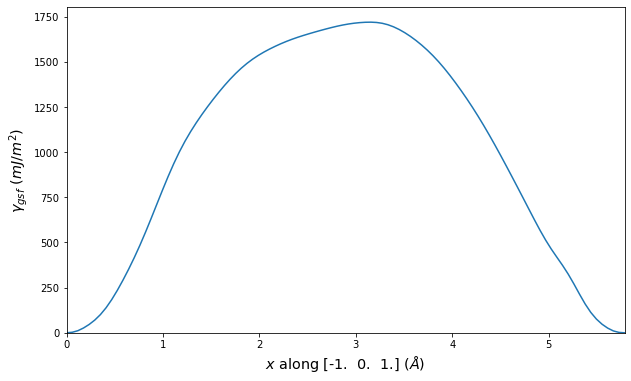
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/3 [-1 2 -1 0] | 103.53 |
| E_usf a/3 [-2 1 1 3] | 214.60 |
| τ_ideal a/3 [-1 2 -1 0] | 2.49 |
| τ_ideal a/3 [-2 1 1 3] | 3.72 |
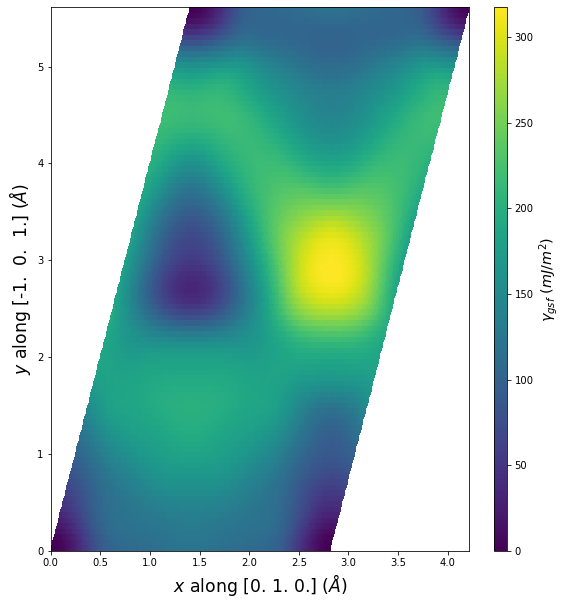
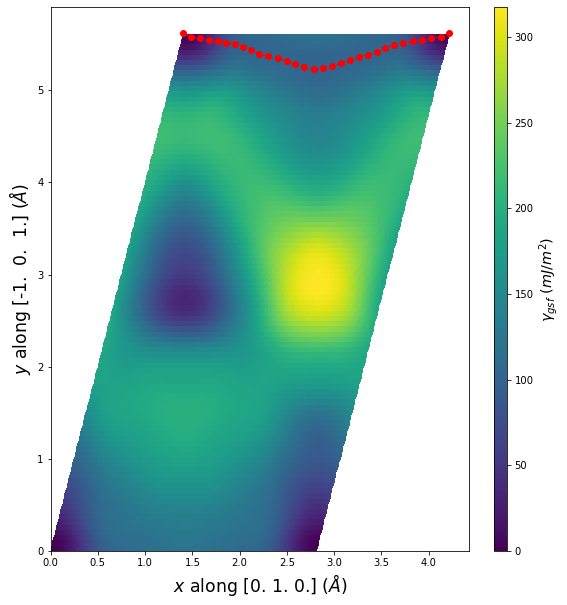
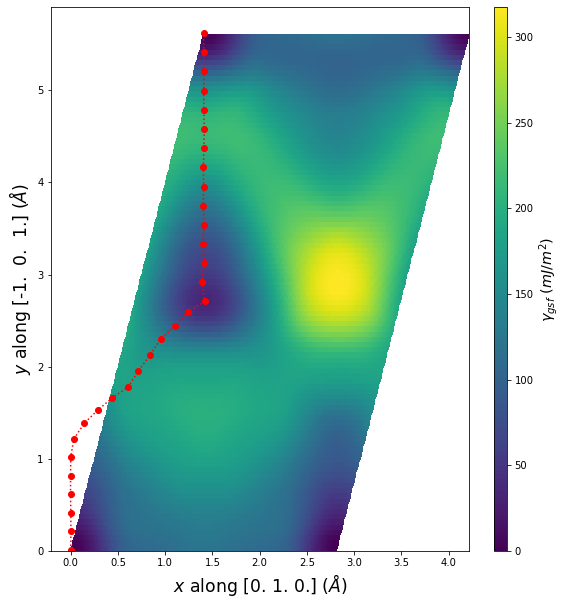
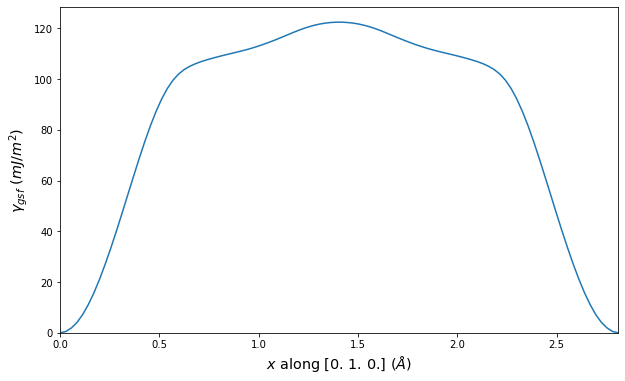
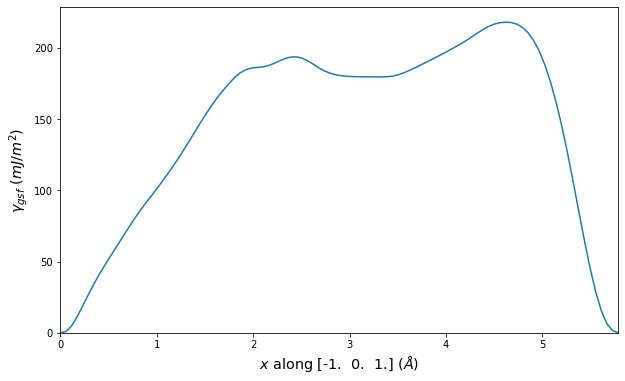
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/3 [-2 1 1 3] | 318.25 |
| τ_ideal a/3 [-2 1 1 3] | 3.96 |
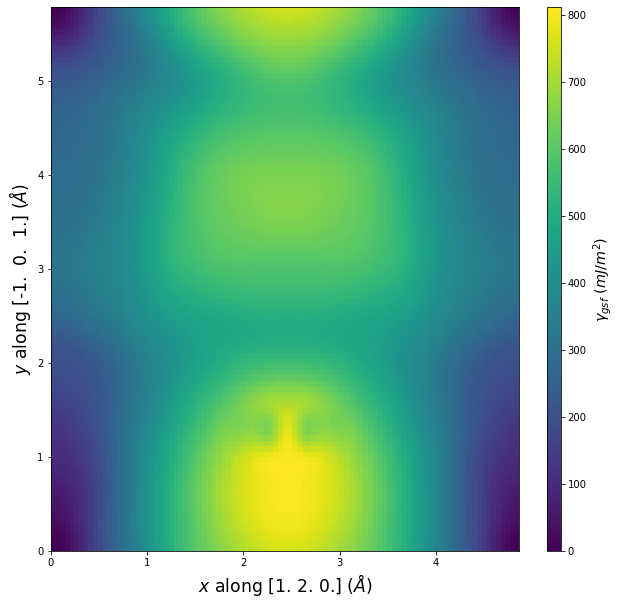
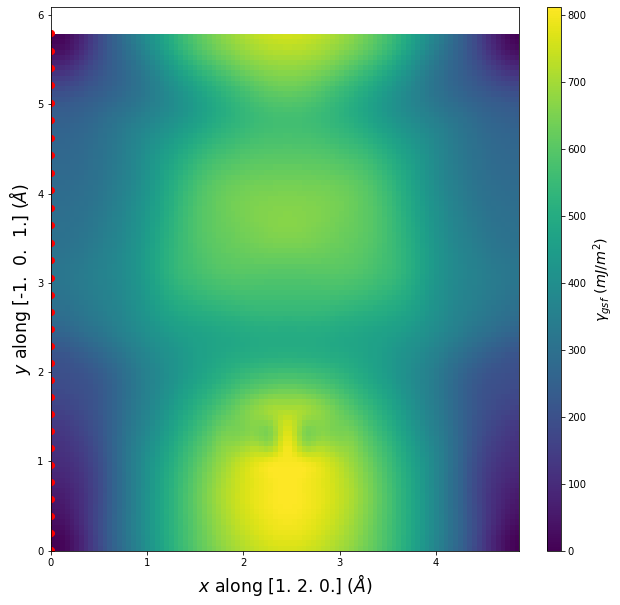
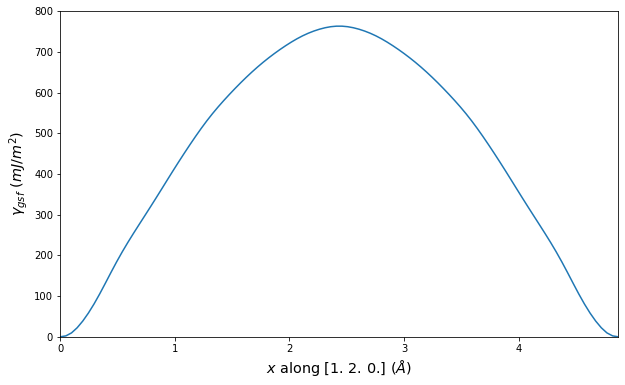
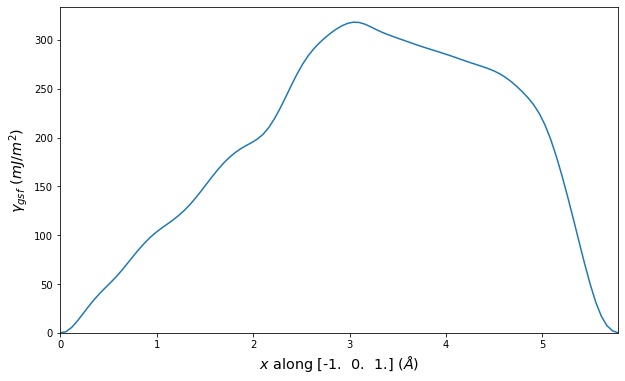
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [0 -1 1] | 829.81 |
| τ_ideal a/2 [0 -1 1] | 12.67 |
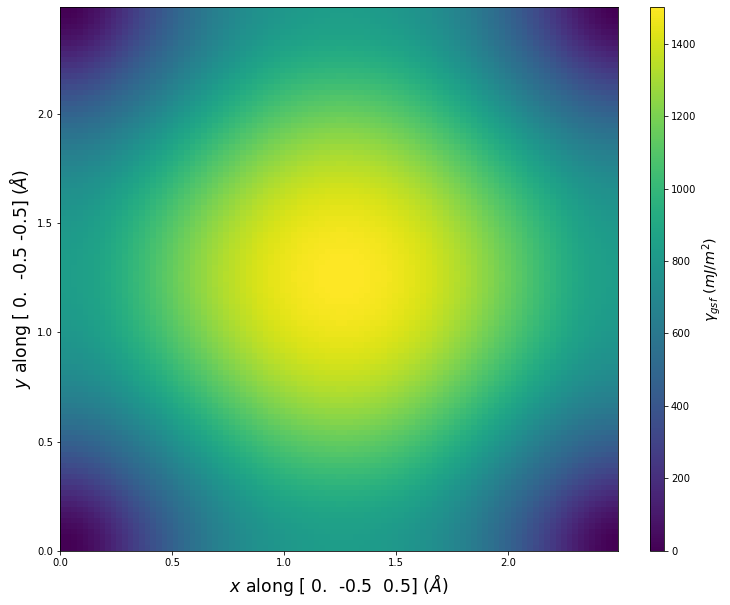
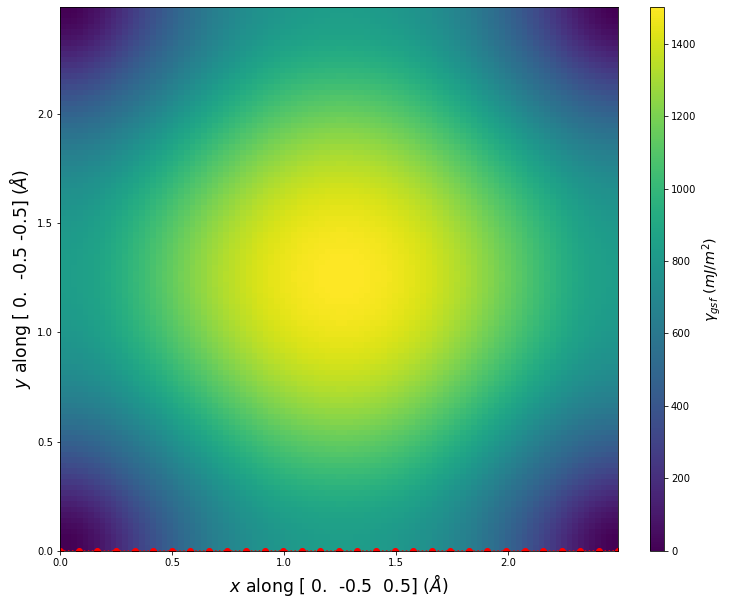
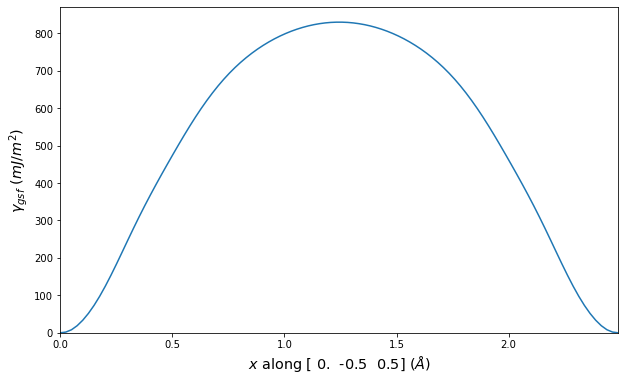
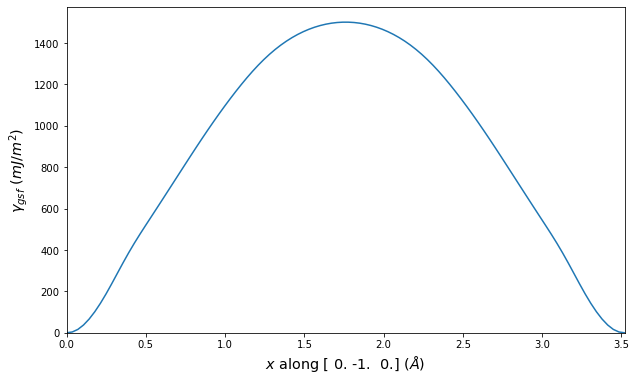
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_isf | 88.79 |
| E_usf a/2 [0 -1 1] | 212.30 |
| τ_ideal a/2 [0 -1 1] | 4.79 |
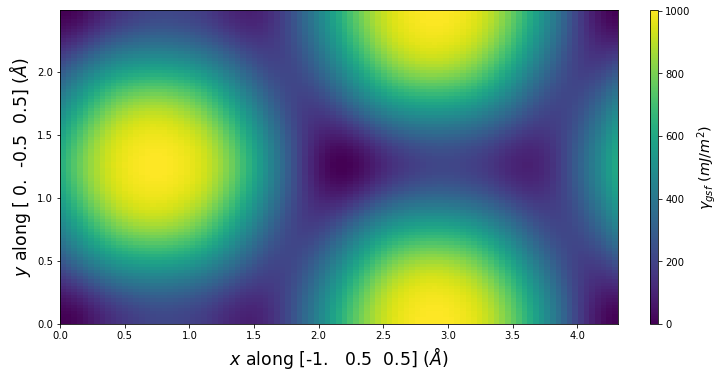
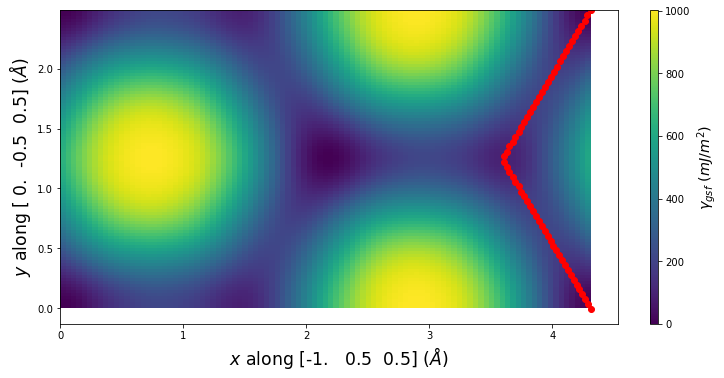
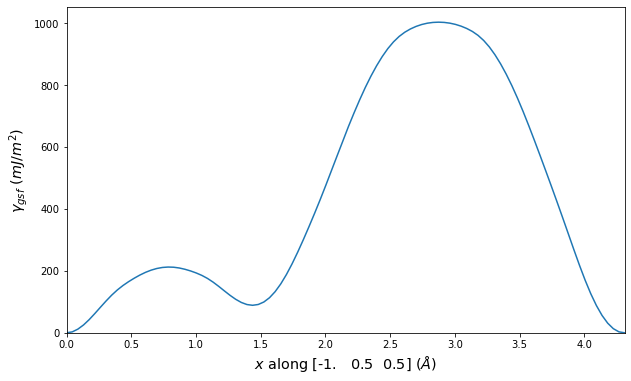
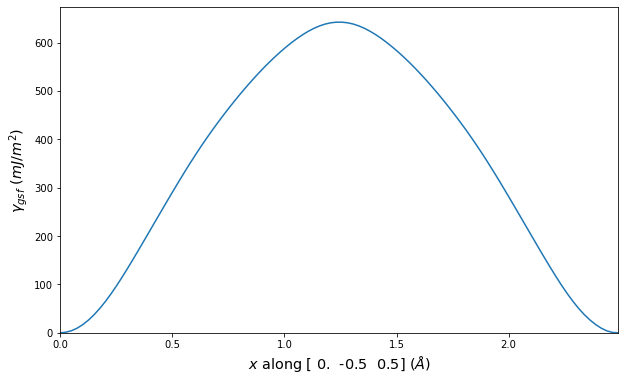
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [-1 1 -1] | 232.75 |
| τ_ideal a/2 [-1 1 -1] | 5.34 |
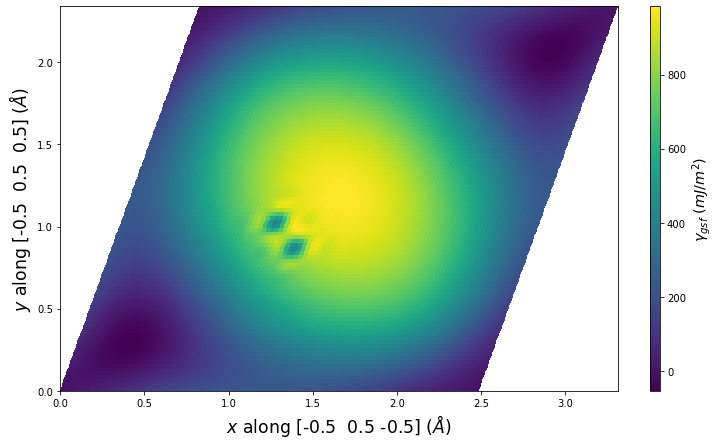
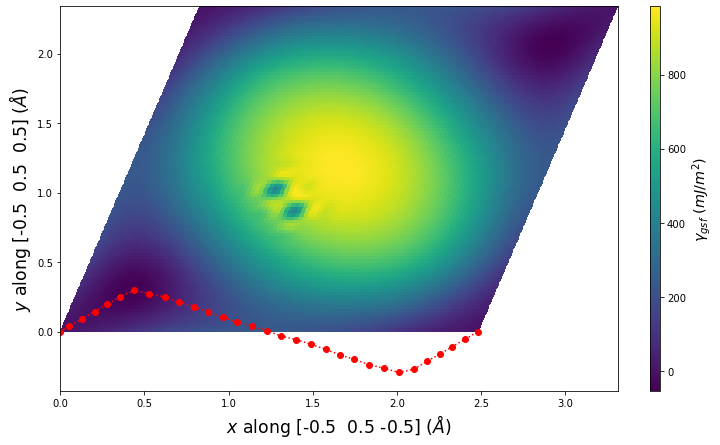
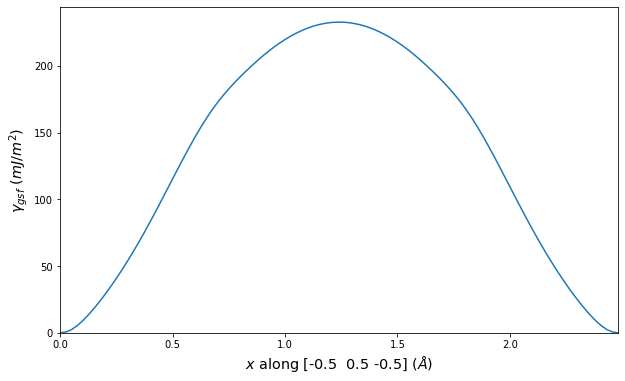
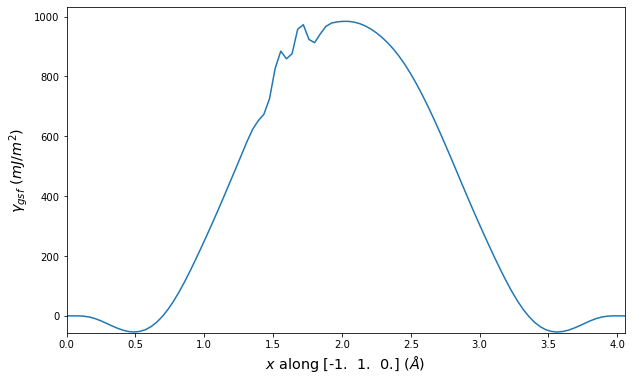
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [-1 -1 1] | 301.37 |
| τ_ideal a/2 [-1 -1 1] | 5.06 |
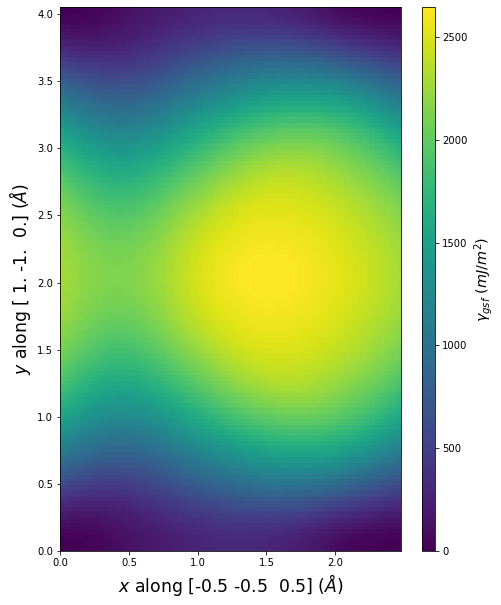
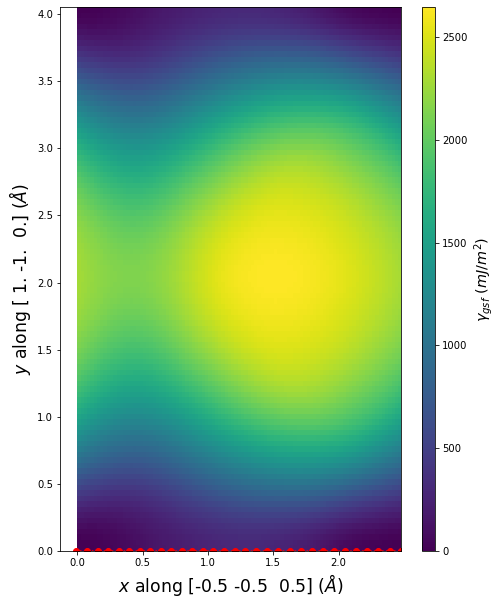
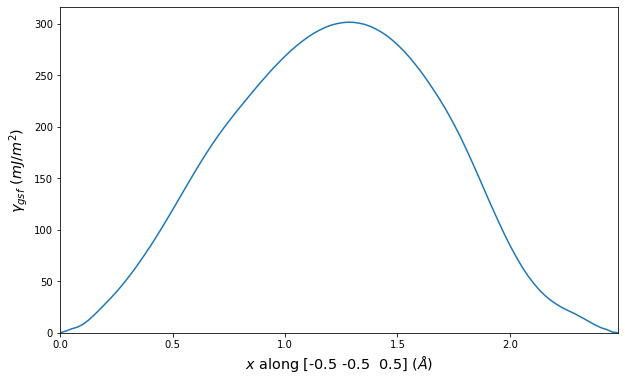
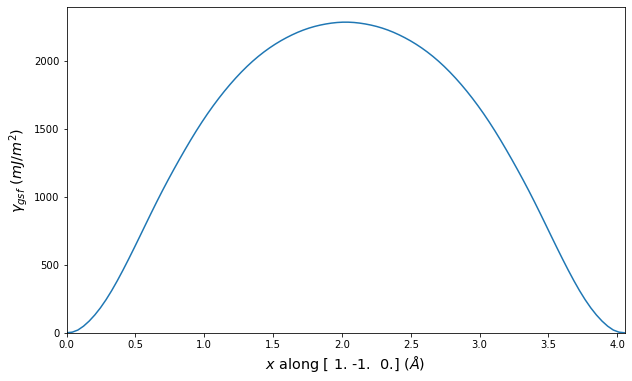
Stacking fault energies in mJ/m2 and ideal shears in GPa
| E_usf a/2 [-1 -1 1] | 288.01 |
| τ_ideal a/2 [-1 -1 1] | 4.93 |
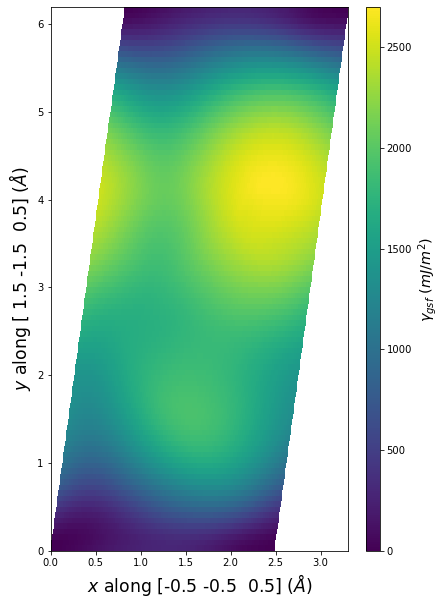
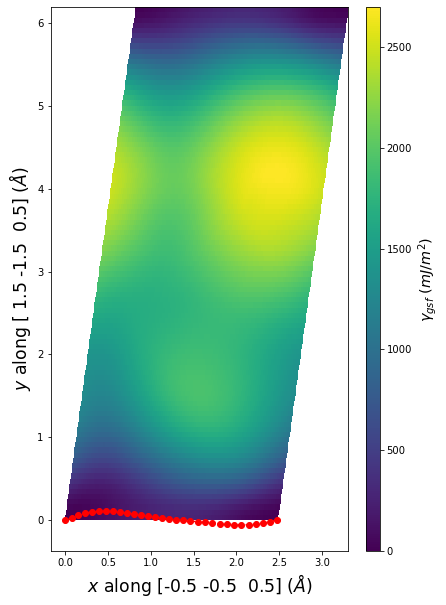
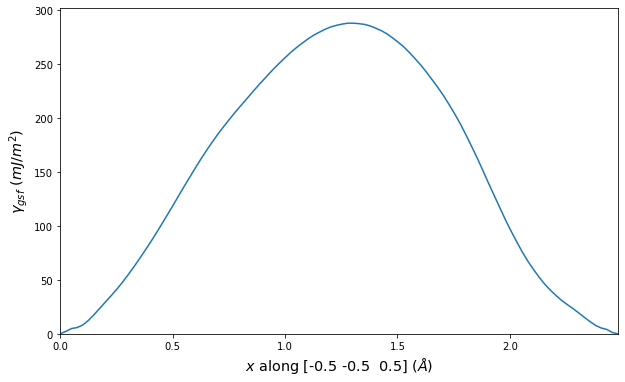
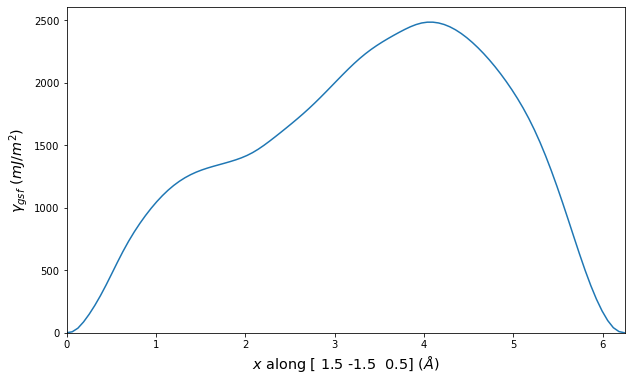
Point Defect Formation Energy Predictions
Static point defect formation energies, Ef, and elastic dipole tensors, pij, are displayed for select crystals. Relaxed defect configurations are obtained by taking a 12x12x12 supercell of a perfect periodic bulk crystal, inserting the point defect, and using force minimization to statically relax the atomic positions while keeping the system dimensions constant. Ef is computed by comparing the energy of the defect system to the same number of atoms in a perfect bulk crystal. pij is estimated as the difference in the system's global pressure with and without the defect multiplied by the system's volume.
Simple structural comparisons of the unrelaxed and relaxed defect configurations are used to help determine if the defect structure has relaxed to a different configuration. Relaxed structures that are identified as no longer consistent with the ideal defect definition are excluded from the table below. The only exception to this is if the lowest energy interstitial configuration does not coincide with a known ideal defect, its energies and pressure tensor are included under the listing "relaxed interstitial". The full list of calculation results including the transformed structures and the structural comparison values is included in the csv file available from the "Download raw data" link.
The calculation method used is available as the iprPy point_defect_static calculation method.
Notes and Disclaimers:
- These values are meant to be guidelines for comparing potentials, not the absolute values for any potential's properties. Values listed here may change if the calculation methods are updated due to improvements/corrections. Variations in the values may occur for changes in calculation methods, simulation software and implementations of the interatomic potentials.
- The computed formation energy and elastic dipole tensor values are sensitive to the size of the system used. The 12x12x12 supercell size was selected as it should provide a decent approximation of the true bulk values.
- The tests for identifying configuration relaxations are not guaranteed to be comprehensive or suitable for all point defect types. The table only shows the point defects that are consistent with the ideal configurations for that defect type, and the lowest energy interstitial.
- The "relaxed interstitial" label indicates that the structure is not consistent with any of the known ideal interstitial configurations. No information is provided as to what that relaxed strucutre is, whether it is an unknown structure, a "near"-ideal defect, or a collapse to amorphous.
- NIST disclaimer
| Point Defect | Ef (eV) | p11 (eV) | p22 (eV) | p33 (eV) | p12 (eV) | p13 (eV) | p23 (eV) |
|---|---|---|---|---|---|---|---|
| vacancy | 0.525 | -2.743 | -2.743 | -2.743 | 0.000 | 0.000 | -0.000 |
| 2nn divacancy | 1.010 | -5.601 | -5.601 | -6.109 | -0.000 | 0.000 | -0.000 |
| 1nn divacancy | 1.017 | -7.292 | -5.126 | -5.126 | 0.000 | -0.000 | -0.751 |
| 100 dumbbell | 1.784 | 16.349 | 16.349 | 14.747 | 0.000 | 0.000 | 0.000 |
| octahedral interstitial | 1.831 | 16.120 | 16.120 | 16.120 | -0.000 | -0.000 | -0.000 |
| crowdion interstitial | 1.961 | 16.712 | 16.712 | 16.899 | 6.559 | 0.000 | 0.000 |
| 111 dumbbell | 2.115 | 17.558 | 17.558 | 17.558 | 1.881 | 1.881 | 1.881 |
| tetrahedral interstitial | 2.119 | 18.222 | 18.222 | 18.222 | -0.000 | -0.000 | -0.000 |
| Point Defect | Ef (eV) | p11 (eV) | p22 (eV) | p33 (eV) | p12 (eV) | p13 (eV) | p23 (eV) |
|---|---|---|---|---|---|---|---|
| relaxed interstitial | -196.456 | -1142.457 | -1114.217 | -1142.591 | 41.170 | 53.955 | 33.288 |
| Point Defect | Ef (eV) | p11 (eV) | p22 (eV) | p33 (eV) | p12 (eV) | p13 (eV) | p23 (eV) |
|---|---|---|---|---|---|---|---|
| vacancy | 0.602 | -3.964 | -3.964 | -2.705 | 0.000 | 0.000 | 0.000 |
| relaxed interstitial | 1.116 | 8.707 | 9.405 | 15.165 | 0.605 | -0.321 | -0.556 |
| 0001 dumbbell | 1.206 | 8.832 | 8.832 | 14.963 | -0.000 | 0.000 | 0.000 |
| Point Defect | Ef (eV) | p11 (eV) | p22 (eV) | p33 (eV) | p12 (eV) | p13 (eV) | p23 (eV) |
|---|---|---|---|---|---|---|---|
| vacancy | 1.592 | -2.220 | -2.220 | -2.220 | -0.000 | -0.000 | 0.000 |
| 1nn divacancy | 2.992 | -6.559 | -4.282 | -4.282 | -0.000 | -0.000 | -0.017 |
| 2nn divacancy | 3.125 | -4.797 | -4.797 | -5.062 | -0.000 | -0.000 | 0.000 |
| 100 dumbbell | 4.079 | 22.083 | 22.083 | 22.593 | -0.000 | 0.000 | 0.000 |
| crowdion interstitial | 4.372 | 21.251 | 21.251 | 26.305 | 12.795 | -0.000 | 0.000 |
| octahedral interstitial | 4.375 | 23.285 | 23.285 | 23.285 | -0.000 | -0.000 | 0.000 |
| 110 dumbbell | 4.377 | 26.281 | 21.409 | 21.409 | 0.000 | 0.000 | 12.785 |
| 111 dumbbell | 4.487 | 22.320 | 22.320 | 22.320 | 4.954 | 4.954 | 4.954 |
| tetrahedral interstitial | 4.548 | 23.145 | 23.145 | 23.145 | 0.000 | 0.000 | 0.000 |
| Point Defect | Ef (eV) | p11 (eV) | p22 (eV) | p33 (eV) | p12 (eV) | p13 (eV) | p23 (eV) |
|---|---|---|---|---|---|---|---|
| vacancy | 1.301 | -25.358 | -25.358 | -25.358 | -0.000 | 0.000 | -0.000 |
Dislocation Monopole Structures
Plots of the atomic structure of dislocation cores are shown here. The dislocations were constructed using dislocation monopole configurations in which a straight dislocation is created in the center of the system using anisotropic elasticity and the elastic constants computed above. A cylindrical region centered around the dislocation is allowed to relax while the remaining atoms are held fixed. The relaxation consists of 1 million NVT steps at 10 K followed by an energy/force minimization. The final plots show the atomic configuration near the center of the monopole system, and display differential displacement arrows and Nye tensor color maps that are both taken with respect to the Burgers vector direction.
These plots show a wide range of final structures, some corresponding to expected dislocation structures and others not. While the characterizations are dislocation-type dependent, some general classification guidelines are listed here.
- Planar dislocations exist on a single slip plane, which results in a grouping of large differential displacement arrows between two atomic rows. All edge dislocations and some screw dislocations may be planar dislocations.
- Non-planar dislocations are screw dislocations that are positioned at the intersection of more than one slip plane. This results in the differential displacement arrows circling the position of the dislocation core. These core structures often have rotational symmetry due to the intersecting planes.
- The plotted atomic positions are also useful for characterizing the final configuration. For screw dislocations, the atomic projections should match projections in the bulk crystal if the crystal has not transformed. For edge dislocations, the projections should be the bulk projections with the extra half-plane of atoms directly above the dislocation core.
- Images in which the atomic positions look correct but no large differential displacement arrows are observed are likely the result of the dislocation gliding out of view during relaxation.
- Phase transformations are identified by large differential displacement arrows spread out in both plot directions, often across the whole image. Additionally, the atomic position projections will likely not correspond to what is expected.
- Twins typically appear as a long line of large differential displacement arrows along a single plane. Note that twins can nucleate phase transformations so the distinction between the two is not always clear.
The calculation method used is available as the iprPy dislocation_monopole calculation method.
Links are provided above the images allowing for users to download the final defect configuration and a corresponding defect-free configuration if they wish to further analyze the structures or use them for subsequent simulations.
Notes and Disclaimers:
- While the general dislocation monopole method is universal to all dislocations, these calculations rely on dislocation-type specific atomic configuration sizes and differential displacement/Nye tensor settings. For the system size, the specific super cell multipliers vary based on the crystal and crystal vector orientations, but the sizes are always selected to minimize the length along the dislocation line and attempt to make the two other box dimensions similar. For the structure analysis tools, both are sensitive to the cutoff distance used to identify neighbors, and both have some method-specific parameters. Where known, the settings used here correspond to the most common ones used in literature.
- For bcc dislocations, the differential displacement vectors shown here are "wrapped" in that if their magnitudes exceed b/2 then a value of b is added/subtracted to wrap the vector back around. This convention reveals the dislocation's structure and location without showing the slip history.
- NIST disclaimer
Version Information:
- 2025-08-07. Plots first added.
MD Solid Property Predictions
Plots of lattice and elastic constants are shown as a function of temperature. The 0K points were taken from the Crystal Structure Predictions and the Elastic Constants Predictions sections above for the unique crystal structures relaxed with the "dynamic" method. Starting from the 0 K relaxed crystal unit cells, supercell systems are created by replicating all three dimensions by the same multiplier to achieve at least 4000 atoms. The systems are then relaxed at 50 K and zero pressure using 1 million NPT steps. Lattice constants are estimated by averaging the measured box dimensions. Temperatures are iteratively increased by 50 K, with each subsequent relaxation calculation starting from the final atomic configuration at the previous temperature and relaxing for another 1 million steps.
The elastic constants are calculated using the deformation–fluctuation hybrid method. Starting from the final atomic configurations of the dynamic relaxations, the system is allowed to evolve at constant volume with a Langevin thermostat. The Born matrix is computed during this run by evaluating how the atomic forces would vary due to applied linear strain fields. The elastic constants can then be estimated using the averaged Born matrix values and the averaged stresses on the system.
The calculation methods used are available as the iprPy relax_dynamic and elastic_constants_dynamic calculation methods.
Clicking on the image of a plot will open an interactive version of it in a new tab. The underlying data for the plots can be downloaded by clicking on the links above each plot.
Notes and Disclaimers:
- The maximum temperature shown for a crystal either corresponds to the maximum value that has been computed so far, or the maximum value that the structure is believed to have remained untransformed. The unstable/transformation temperature identification is mostly automated and can miss transitions not associated with large discontinuities in property values with changing temperature.
- For succinctness, the elastic constants displayed here are averaged according to the 0 K structure's crystal symmetry family. If the structures deviate from the expected symmetry at higher temperatures, the values may not be valid. Raw results are available for verification if requested.
- NIST disclaimer
Version Information:
- 2025-08-07. Plots added.
MD Liquid Property Predictions
Plots of radial distribution functions at different temperatures and the temperature-dependent diffusion and viscosity are shown here for elemental liquids. Melt phases are constructed by starting with a 10x10x10 fcc super cell and relaxing with 50,000 NPT steps at zero pressure and a high melting temperature (3000 K for most potentials and elements). Following the melt, liquid structures are relaxed by running NPT for 10,000 steps over which the temperature is dropped by 50 K, then 50,000 NPT at the target temperature to estimate the equilibrium volume, followed by 20,000 NVT steps at the averaged equilibrium volume and target temperature. Structures from the NVT run are sampled to compute the radial distribution function of the liquid at the corresponding temperature.
The final relaxed configurations at each temperature explored are used as the initial configurations for the diffusion and viscosity calculations. For diffusion, the system is integrated for 100 runs of 2,000 NVT steps during which both the mean squared displacement (MSD) and the velocity auto correlation function (VACF) are computed. From these simulations, three estimates of diffusion are computed: one from the MSD of the full 200,000 step run, one in which the MSD is reset for each short run and then averaged, and one from the VACF computed for each short run and averaged. For viscosity, the Green-Kubo method is used which is evaluated during a 1 million step NVT run.
The calculation methods used are available as the iprPy relax_liquid_redo, diffusion_liquid, and viscosity_green_kubo calculation methods.
Clicking on the image of a plot will open an interactive version of it in a new tab. The underlying data for the plots can be downloaded by clicking on the links above each plot.
Notes and Disclaimers:
- The current liquid relaxation has some known issues, and therefore may be recalculated with an improved method later. Most notably, the unconstrained NPT relaxation may lead to one of the periodic dimensions becoming quite small which can negatively affect the simulations and property calculations. Additionally, the relaxations likely need to be longer to reduce the error associated with the measured volume and energy values.
- Values are only displayed down to the last temperature currently calculated, or the last temperature at which the system is believed to remain liquid until the end of all simulations. The transformation temperature is estimated by looking at discontinuities in the measured property values and may incorrectly predict a phase to still be liquid if the discontinuities are small.
- The three diffusion estimates provide a range of prediction values. For MSD, the longer the run the more likely it is that a small number of atoms will diffuse much farther than the rest, which skews the squared displacement higher.
- NIST disclaimer
Version Information:
- 2025-08-07. Plots added. Data should be thought of as preliminary as results may be recalculated later.
Melting Temperature Estimates
Estimated melting temperatures are tabulated below. The melting temperature is computed here using a two-phase solid-liquid atomic configuration. The two-phase configuration is created by starting with a crystalline system in which the c box vector is roughly twice the length of the other two box vectors. Based on some input temperature Tinit, an NPH plus a Berensen thermostat simulation is performed for 10,000 steps in which half the system is subjected to a temperature of 1.25*Tinit and the other half to a temperature of 0.5*Tinit. This is then followed by 10,000 steps during which the temperature of the two regions are both scaled to Tinit. The system is then ran for 200,000 NPH steps to equilibrate the system. For the second half of the final NPH run, the average temperature of the system is calculated and the polyhedral template matching algorithm is used to estimate the number of solid and liquid atoms for a number of configuration snapshots. If the averaged fraction of solid atoms is found to be between 0.25-0.75, then the averaged temperature provides an estimate of the melting temperature.
This calculation is iteratively performed where the Tinit value is adjusted up or down if the fraction of solid atoms is outside the range 0.25-0.75. Iterations are repeated until 10 calculations are performed that produce solid fractions in the target range, or 30 total calculations are performed.
The calculation method used is available as the iprPy melting_temperature calculation method.
Notes and Disclaimers:
- Results are displayed below based on the crystal structure used. Different crystal structures may result in different melting temperature estimates.
- The polyhedral template matching algorithm only works for certain crystal prototypes and requires specifying to the algorithm which crystal structures are expected. Here, the algorithm is set to only look for the specific crystal structure used, meaning that the solid/liquid ratio measured is technically the crystal/something-else ratio.
- NIST disclaimer
Version Information:
- 2025-08-07. Values first added.
| prototype | Tmelt | stderr |
|---|---|---|
| A1--Cu--fcc | 313.83 | 0.43 |
| prototype | Tmelt | stderr |
|---|---|---|
| A1--Cu--fcc | 1432.45 | 1.24 |
MD Thermodynamic Predictions
Plots of internal energy, Gibbs free energy, entropy, heat capacity and volume are shown here as a function of temperature for various crystal structures and liquid phases. The included crystal structures correspond to those in the Solid Structures vs. Temperature section, and the liquid phases to those in the Liquid Properties section. Internal energy and volume are taken from the associated structure relaxations mentioned in those previous sections. Constant pressure heat capacity is estimated using 3-point numerical derivatives of enthalpy versus temperature. Note that since all simulations done here are at 0 pressure, internal energy and enthalpy are equivalent.
The Gibbs energies of the phases are estimated using thermodynamic integration between the interatomic potential in question and a simpler model with known Gibbs free energy values. For solids, the reference model is an Einstein solid, while for liquids it is the Uhlenbeck-Ford potential. Besides a short run at the start of the solid calculations to estimate Einstein model spring constants, the two calculations proceed similarly. Starting with the final relaxation configurations, the systems are stabilized for 25,000 steps. Then, over the next 50,000 steps the potential is swapped out for the reference potential. The system is then stabilized for another 25,000 steps with the reference model before a reverse swap of 50,000 steps is performed. The simulation ends with one final 25,000 step stabilization period. From the simulation, the irreversible work of transformation is estimated and used to compute the absolute Gibbs free energy of the target phase and potential relative to the reference potential. Entropy is estimated as the difference in enthalpy and Gibbs free energy and divided by temperature.
The calculation methods used are available as the iprPy relax_dynamic, relax_liquid_redo, free_energy, and free_energy_liquid calculation methods.
Clicking on the image of a plot will open an interactive version of it in a new tab. The underlying data for the plots can be downloaded by clicking on the links above each plot.
Notes and Disclaimers:
- Good free energy estimates require that the initial and final phases before and after the thermodynamic integration remain the same. This is not an issue with the liquid calculations as the Uhlenbeck-Ford model always predicts a liquid, but may be an issue for the solid phase estimates. This is likely to be an issue for non-compact phases which the Einstein model is poor at representing.
- NIST disclaimer
Version Information:
- 2025-08-07. Plots added.