phonon - Methodology and code
Python imports
[1]:
# Standard library imports
from pathlib import Path
import os
import sys
import uuid
import shutil
import datetime
from collections import OrderedDict
from math import floor
from copy import deepcopy
from typing import Optional, Tuple
# http://www.numpy.org/
import numpy as np
# https://ipython.org/
from IPython.display import display, Markdown, Image
# https://matplotlib.org/
import matplotlib.pyplot as plt
# https://atztogo.github.io/spglib/python-spglib.html
import spglib
# https://atztogo.github.io/phonopy/phonopy-module.html
import phonopy
# https://github.com/usnistgov/DataModelDict
from DataModelDict import DataModelDict as DM
# https://github.com/usnistgov/atomman
import atomman as am
import atomman.lammps as lmp
import atomman.unitconvert as uc
from atomman.tools import filltemplate
# https://github.com/usnistgov/iprPy
import iprPy
from iprPy.tools import read_calc_file
print('Notebook last executed on', datetime.date.today(), 'using iprPy version', iprPy.__version__)
Notebook last executed on 2023-07-31 using iprPy version 0.11.6
1. Load calculation and view description
1.1. Load the calculation
[2]:
# Load the calculation being demoed
calculation = iprPy.load_calculation('phonon')
1.2. Display calculation description and theory
[3]:
# Display main docs and theory
display(Markdown(calculation.maindoc))
display(Markdown(calculation.theorydoc))
phonon calculation style
Lucas M. Hale, lucas.hale@nist.gov, Materials Science and Engineering Division, NIST.
Introduction
The phonon calculation style applies small atomic displacements to a unit cell system and evaluates the forces on the atoms to evaluate phonon-based properties.
Version notes
2020-12-21: Script extended to include quasiharmonic calculations.
2022-03-11: Notebook updated to reflect version 0.11.
Additional dependencies
Disclaimers
Method and Theory
Starting with an initial system, spglib is used to identify the associated primitive unit cell. The primitive cell is passed to phonopy, which constructs super cell systems with small atomic displacements. A LAMMPS calculation is performed on the displaced systems to evaluate the atomic forces on each atom without relaxing. The measured atomic forces are then passed back to phonopy, which computes force constants for the system. Plots are then created for the band structure, density of states, and other thermal properties.
See phonopy documentation for more details about the package and the associated theory.
2. Define calculation functions and generate files
This section defines the calculation functions and associated resource files exactly as they exist inside the iprPy package. This allows for the code used to be directly visible and modifiable by anyone looking to see how it works.
2.1. phonon_quasiharmonic()
This is the primary function for the calculation. The version of this function built in iprPy can be accessed by calling the calc() method of an object of the associated calculation class.
[4]:
def phonon_quasiharmonic(lammps_command: str,
ucell: am.System,
potential: lmp.Potential,
mpi_command: Optional[str] = None,
a_mult: int = 2,
b_mult: int = 2,
c_mult: int = 2,
distance: float = 0.01,
symprec: float = 1e-5,
strainrange: float = 0.01,
numstrains: int = 5) -> dict:
"""
Function that performs phonon and quasiharmonic approximation calculations
using phonopy and LAMMPS.
Parameters
----------
lammps_command :str
Command for running LAMMPS.
ucell : atomman.System
The unit cell system to perform the calculation on.
potential : atomman.lammps.Potential
The LAMMPS implemented potential to use.
mpi_command : str, optional
The MPI command for running LAMMPS in parallel. If not given, LAMMPS
will run serially.
a_mult : int, optional
The a size multiplier to use on ucell before running the phonon
calculation. Must be an int and not a tuple. Default value is 2.
b_mult : int, optional
The b size multiplier to use on ucell before running the phonon
calculation. Must be an int and not a tuple. Default value is 2.
c_mult : int, optional
The c size multiplier to use on ucell before running the phonon
calculation. Must be an int and not a tuple. Default value is 2.
distance : float, optional
The atomic displacement distance used for computing the phonons.
Default value is 0.01.
symprec : float, optional
Absolute length tolerance to use in identifying symmetry of atomic
sites and system boundaries. Default value is 1e-5.
strainrange : float, optional
The range of strains to apply to the unit cell to use with the
quasiharmonic calculations. Default value is 0.01.
numstrains : int, optional
The number of strains to use for the quasiharmonic calculations.
Must be an odd integer. If 1, then the quasiharmonic calculations
will not be performed. Default value is 5.
"""
# Get lammps units
lammps_units = lmp.style.unit(potential.units)
# Get lammps version date
lammps_date = lmp.checkversion(lammps_command)['date']
# Convert ucell to a primitive cell
ucell = ucell.dump('primitive_cell', symprec=symprec)
# Get unstrained box vectors
vects = ucell.box.vects
# Generate the range of strains
if numstrains == 1:
zerostrain = phononcalc(lammps_command, ucell, potential,
mpi_command=mpi_command,
a_mult=a_mult, b_mult=b_mult, c_mult=c_mult,
distance=distance, symprec=symprec,
lammps_date=lammps_date)
phonons = [zerostrain['phonon']]
qha = None
elif numstrains % 2 == 0 or numstrains < 5:
raise ValueError('Invalid number of strains: must be odd and 1 or >= 5')
else:
strains = np.linspace(-strainrange, strainrange, numstrains)
istrains = np.linspace(-(numstrains-1)/2, (numstrains-1)/2, numstrains, dtype=int)
volumes = []
energies = []
phonons = []
temperatures = None
free_energy = None
heat_capacity = None
entropy = None
# Loop over all strains
for i in range(numstrains):
strain = strains[i]
if numstrains != 1:
istrain = f'_{istrains[i]}'
else:
istrain = ''
# Identify the zero strain run
if istrains[i] == 0:
zerostrainrun = True
else:
zerostrainrun = False
# Generate system at the strain
newvects = vects * (1 + strain)
ucell.box_set(vects=newvects, scale=True)
volumes.append(ucell.box.volume)
system = ucell.supersize(a_mult, b_mult, c_mult)
# Define lammps variables
lammps_variables = {}
system_info = system.dump('atom_data', f='disp.dat',
potential=potential)
lammps_variables['atomman_system_pair_info'] = system_info
# Set dump_modify_format based on lammps_date
if lammps_date < datetime.date(2016, 8, 3):
lammps_variables['dump_modify_format'] = '"%d %d %.13e %.13e %.13e %.13e %.13e %.13e"'
else:
lammps_variables['dump_modify_format'] = 'float %.13e'
# Write lammps input script
lammps_script = 'phonon.in'
template = read_calc_file('iprPy.calculation.phonon', 'phonon.template')
with open(lammps_script, 'w') as f:
f.write(filltemplate(template, lammps_variables, '<', '>'))
# Run LAMMPS
output = lmp.run(lammps_command, script_name='phonon.in',
mpi_command=mpi_command)
# Extract system energy
thermo = output.simulations[0]['thermo']
energy = uc.set_in_units(thermo.PotEng.values[-1], lammps_units['energy'])
# Scale energy by sizemults and append to list
energies.append(energy / (a_mult * b_mult * c_mult))
# Compute phonon info for ucell
phononinfo = phononcalc(lammps_command, ucell, potential, mpi_command=mpi_command,
a_mult=a_mult, b_mult=b_mult, c_mult=c_mult,
distance=distance, symprec=symprec, istrain=istrain,
plot=zerostrainrun, lammps_date=lammps_date)
phonons.append(phononinfo['phonon'])
# Extract temperature values from the first run
if temperatures is None:
temperatures = phononinfo['thermal_properties']['temperatures']
# Initialize QHA input arrays
free_energy = np.empty((len(temperatures), len(strains)))
heat_capacity = np.empty((len(temperatures), len(strains)))
entropy = np.empty((len(temperatures), len(strains)))
# Get values for zerostrainrun
if zerostrainrun is True:
zerostrain = phononinfo
# Copy values to qha input arrays
free_energy[:, i] = phononinfo['thermal_properties']['free_energy']
entropy[:, i] = phononinfo['thermal_properties']['entropy']
heat_capacity[:, i] = phononinfo['thermal_properties']['heat_capacity']
# Try to compute qha
try:
eos = 'vinet'
qha = phonopy.PhonopyQHA(volumes=volumes,
electronic_energies=energies,
temperatures=temperatures,
free_energy=free_energy,
cv=heat_capacity, eos=eos,
entropy=entropy)
except:
try:
eos = 'birch_murnaghan'
qha = phonopy.PhonopyQHA(volumes=volumes,
electronic_energies=energies,
temperatures=temperatures,
free_energy=free_energy,
cv=heat_capacity, eos=eos,
entropy=entropy)
except:
qha = None
results = {}
# Add phonopy objects
results['phonon_objects'] = phonons
results['qha_object'] = qha
# Extract zerostrain properties
results['band_structure'] = zerostrain['band_structure']
results['density_of_states'] = zerostrain['dos']
# Convert units on thermal properties
results['thermal_properties'] = zerostrain['thermal_properties']
results['thermal_properties']['temperature'] = results['thermal_properties'].pop('temperatures')
results['thermal_properties']['Helmholtz'] = uc.set_in_units(results['thermal_properties'].pop('free_energy'), 'kJ/mol')
results['thermal_properties']['entropy'] = uc.set_in_units(results['thermal_properties'].pop('entropy'), 'J/K/mol')
results['thermal_properties']['heat_capacity_v'] = uc.set_in_units(results['thermal_properties'].pop('heat_capacity'), 'J/K/mol')
if qha is not None:
results['qha_eos'] = eos
# Create QHA plots
qha.plot_bulk_modulus()
plt.xlabel('Volume ($Å^3$)', size='large')
plt.ylabel('Energy ($eV$)', size='large')
plt.savefig('bulk_modulus.png', dpi=400, bbox_inches='tight')
plt.close()
qha.plot_helmholtz_volume()
plt.savefig('helmholtz_volume.png', dpi=400)
plt.close()
# Package volume vs energy scans
results['volume_scan'] = {}
results['volume_scan']['volume'] = np.array(volumes)
results['volume_scan']['strain'] = strains
results['volume_scan']['energy'] = np.array(energies)
# Compute and add QHA properties
properties = qha.get_bulk_modulus_parameters()
results['E0'] = uc.set_in_units(properties[0], 'eV')
results['B0'] = uc.set_in_units(properties[1], 'eV/angstrom^3')
results['B0prime'] = uc.set_in_units(properties[2], 'eV/angstrom^3')
results['V0'] = uc.set_in_units(properties[3], 'angstrom^3')
results['thermal_properties']['volume'] = uc.set_in_units(np.hstack([qha.volume_temperature, np.nan]), 'angstrom^3')
results['thermal_properties']['thermal_expansion'] = np.hstack([qha.thermal_expansion, np.nan])
results['thermal_properties']['Gibbs'] = uc.set_in_units(np.hstack([qha.gibbs_temperature, np.nan]), 'eV')
results['thermal_properties']['bulk_modulus'] = uc.set_in_units(np.hstack([qha.bulk_modulus_temperature, np.nan]), 'GPa')
results['thermal_properties']['heat_capacity_p_numerical'] = uc.set_in_units(np.hstack([qha.heat_capacity_P_numerical, np.nan]), 'J/K/mol')
results['thermal_properties']['heat_capacity_p_polyfit'] = uc.set_in_units(np.hstack([qha.heat_capacity_P_polyfit, np.nan]), 'J/K/mol')
results['thermal_properties']['gruneisen'] = np.hstack([qha.gruneisen_temperature, np.nan])
return results
2.2. phononcalc()
[5]:
def phononcalc(lammps_command: str,
ucell: am.System,
potential: lmp.Potential,
mpi_command: Optional[str] = None,
a_mult: int = 2,
b_mult: int = 2,
c_mult: int = 2,
distance: float = 0.01,
symprec: float = 1e-5,
istrain: str = '',
plot: bool = True,
lammps_date: Optional[datetime.date] = None) -> dict:
"""
Uses phonopy to compute the phonons for a unit cell structure using a
LAMMPS interatomic potential.
Parameters
----------
lammps_command :str
Command for running LAMMPS.
ucell : atomman.System
The unit cell system to perform the calculation on.
potential : atomman.lammps.Potential
The LAMMPS implemented potential to use.
mpi_command : str, optional
The MPI command for running LAMMPS in parallel. If not given, LAMMPS
will run serially.
a_mult : int, optional
The a size multiplier to use on ucell before running the phonon
calculation. Must be an int and not a tuple. Default value is 2.
b_mult : int, optional
The b size multiplier to use on ucell before running the phonon
calculation. Must be an int and not a tuple. Default value is 2.
c_mult : int, optional
The c size multiplier to use on ucell before running the phonon
calculation. Must be an int and not a tuple. Default value is 2.
distance : float, optional
The atomic displacement distance used for computing the phonons.
Default value is 0.01.
symprec : float, optional
Absolute length tolerance to use in identifying symmetry of atomic
sites and system boundaries. Default value is 1e-5.
istrain: str, optional
A string to add to saved yaml files to ensure their uniqueness for the
different strains explored by QHA. Default value is '', which assumes
only one calculation is being performed.
plot : bool, optional
Flag indicating if band structure and DOS figures are to be generated.
Default value is True.
lammps_date : datetime.date, optional
The version date associated with lammps_command. If not given, the
version will be identified.
"""
# Get lammps units
lammps_units = lmp.style.unit(potential.units)
# Get lammps version date
if lammps_date is None:
lammps_date = lmp.checkversion(lammps_command)['date']
# Convert ucell to a primitive cell
ucell = ucell.dump('primitive_cell', symprec=symprec)
# Initialize Phonopy object
phonon = phonopy.Phonopy(ucell.dump('phonopy_Atoms', symbols=potential.elements(ucell.symbols)),
[[a_mult, 0, 0], [0, b_mult, 0], [0, 0, c_mult]],
factor=phonopy.units.VaspToTHz)
phonon.generate_displacements(distance=distance)
# Loop over displaced supercells to compute forces
forcearrays = []
for supercell in phonon.supercells_with_displacements:
# Save to LAMMPS data file
system = am.load('phonopy_Atoms', supercell, symbols=ucell.symbols)
system_info = system.dump('atom_data', f='disp.dat',
potential=potential)
# Define lammps variables
lammps_variables = {}
lammps_variables['atomman_system_pair_info'] = system_info
# Set dump_modify_format based on lammps_date
if lammps_date < datetime.date(2016, 8, 3):
lammps_variables['dump_modify_format'] = '"%d %d %.13e %.13e %.13e %.13e %.13e %.13e"'
else:
lammps_variables['dump_modify_format'] = 'float %.13e'
# Write lammps input script
lammps_script = 'phonon.in'
template = read_calc_file('iprPy.calculation.phonon', 'phonon.template')
with open(lammps_script, 'w') as f:
f.write(filltemplate(template, lammps_variables, '<', '>'))
# Run LAMMPS
lmp.run(lammps_command, script_name=lammps_script, mpi_command=mpi_command)
# Extract forces from dump file
forcestructure = am.load('atom_dump', 'forces.dump')
forces = uc.set_in_units(forcestructure.atoms.force, lammps_units['force'])
forcearrays.append(forces)
results = {}
# Set computed forces
phonon.forces = forcearrays
# Save to yaml file
phonon.save(f'phonopy_params{istrain}.yaml')
# Compute band structure
phonon.produce_force_constants()
phonon.auto_band_structure(plot=plot)
results['band_structure'] = phonon.get_band_structure_dict()
if plot:
plt.ylabel('Frequency (THz)')
plt.savefig(Path('.', 'band.png'), dpi=400)
plt.close()
# Compute density of states
phonon.auto_total_dos(plot=False)
phonon.auto_projected_dos(plot=False)
dos = phonon.get_total_dos_dict()
dos['frequency'] = uc.set_in_units(dos.pop('frequency_points'), 'THz')
dos['projected_dos'] = phonon.get_projected_dos_dict()['projected_dos']
results['dos'] = dos
# Compute thermal properties
phonon.run_thermal_properties()
results['thermal_properties'] = phonon.get_thermal_properties_dict()
phonon.write_yaml_thermal_properties(filename=f"thermal_properties{istrain}.yaml")
results['phonon'] = phonon
return results
2.3. phonon.template file
[6]:
with open('phonon.template', 'w') as f:
f.write("""# LAMMPS input script that evaluates atomic forces without relaxing
box tilt large
<atomman_system_pair_info>
thermo_style custom step pe
thermo_modify format float %.13e
dump dumpy all custom 1 forces.dump id type x y z fx fy fz
dump_modify dumpy format <dump_modify_format>
run 0""")
3. Specify input parameters
3.1. System-specific paths
lammps_command is the LAMMPS command to use (required).
mpi_command MPI command for running LAMMPS in parallel. A value of None will run simulations serially.
[7]:
lammps_command = 'lmp'
mpi_command = None
# Optional: check that LAMMPS works and show its version
print(f'LAMMPS version = {am.lammps.checkversion(lammps_command)["version"]}')
LAMMPS version = 15 Sep 2022
3.2. Interatomic potential
potential_name gives the name of the potential_LAMMPS reference record in the iprPy library to use for the calculation.
potential is an atomman.lammps.Potential object (required).
[8]:
potential_name = '1999--Mishin-Y--Ni--LAMMPS--ipr1'
# Retrieve potential and parameter file(s)
potential = am.load_lammps_potential(id=potential_name, getfiles=True)
3.3. Initial unit cell system
ucell is an atomman.System representing a fundamental unit cell of the system (required). Here, this is generated using the load parameters and symbols.
[9]:
# Create ucell by loading prototype record
ucell = am.load('crystal', potential=potential, family='A1--Cu--fcc')
print(ucell)
avect = [ 3.520, 0.000, 0.000]
bvect = [ 0.000, 3.520, 0.000]
cvect = [ 0.000, 0.000, 3.520]
origin = [ 0.000, 0.000, 0.000]
natoms = 4
natypes = 1
symbols = ('Ni',)
pbc = [ True True True]
per-atom properties = ['atype', 'pos']
id atype pos[0] pos[1] pos[2]
0 1 0.000 0.000 0.000
1 1 0.000 1.760 1.760
2 1 1.760 0.000 1.760
3 1 1.760 1.760 0.000
3.4. System modifications
sizemults list of three integers specifying how many times the ucell vectors of \(a\), \(b\) and \(c\) are replicated in creating system.
system is an atomman.System to perform the scan on (required).
[10]:
sizemults = [2, 2, 2]
# Generate system by supersizing ucell
system = ucell.supersize(*sizemults)
print('# of atoms in system =', system.natoms)
# of atoms in system = 32
3.5. Calculation-specific parameters
displacementdistance is the displacement distance scalar to use when applying random displacements to the atoms to compute the force constants.
symmetryprecision is the absolute precision tolerance to use in determining crystal symmetry elements for identifying the primitive unit cell.
strainrange is the size of the largest strain used for the quasiharmonic calculations.
numstrains is the number of strain states to use for the quasiharmonic calculation. Needs to be odd and either 1 or greater than or equal to 5. If set to 1, then the quasiharmonic calculations will not be performed.
[11]:
displacementdistance = uc.set_in_units(0.01, 'angstrom')
symmetryprecision = 1e-5
strainrange = 0.01
numstrains = 5
3. Define calculation function(s) and generate template LAMMPS script(s)
4. Run calculation function(s)
[12]:
results_dict = phonon_quasiharmonic(lammps_command, ucell, potential,
mpi_command = mpi_command,
a_mult = sizemults[0],
b_mult = sizemults[1],
c_mult = sizemults[2],
distance = displacementdistance,
symprec = symmetryprecision,
strainrange = strainrange,
numstrains = numstrains)
[13]:
results_dict.keys()
[13]:
dict_keys(['phonon_objects', 'qha_object', 'band_structure', 'density_of_states', 'thermal_properties', 'qha_eos', 'volume_scan', 'E0', 'B0', 'B0prime', 'V0'])
5. Report results
The calculation both returns results_dict containing phonon information and generates files.
5.1. Phonon properties
In results_dict:
phonon_objects is a list containing all of the Phonopy objects at all of the strains evaluated.
band_structure contains the evaluated band structure points for the zero strain structure.
density_of_states contains the evaluated density of states (both total and projected) for the zero strain structure.
thermal_properties contains the temperature-dependent Helmholtz free energy, entropy, and constant volume heat capacity.
Generated files:
band.png plots the band structure for the zero strain structure.
phonopy_params.yaml is the YAML-formatted Phonopy data that can be read back in to generate a Phonopy object later.
5.2. Quasiharmonic properties
These are only generated if numstrains is greater than 1.
In results_dict:
qha_object is the PhonopyQHA object.
volume_scan contains the energy versus volume evaluations taken from the different strain states.
E0, B0, B0prime, V0 are the energy, Bulk modulus, B’ modulus, and volume associated with the interpolated equilibrium state from the volume scan.
thermal_properties is expanded to also include the temperature-dependent volume, thermal expansion, Gibbs free energy, bulk modulus, constant pressure heat capacity, and Grüneisen parameter.
Generated files:
bulk_modulus.png plots the volume scan data as it is used to estimate the bulk modulus. This plot provides a quick visual means of telling if the quasiharmonic analysis is likely good for the strains explored.
helmholtz.png plots the helmholtz free energy versus volume.
phonopy_params_*.yaml are the YAML-formatted Phonopy data for the non-zero strains that can be read back in to generate Phonopy objects later.
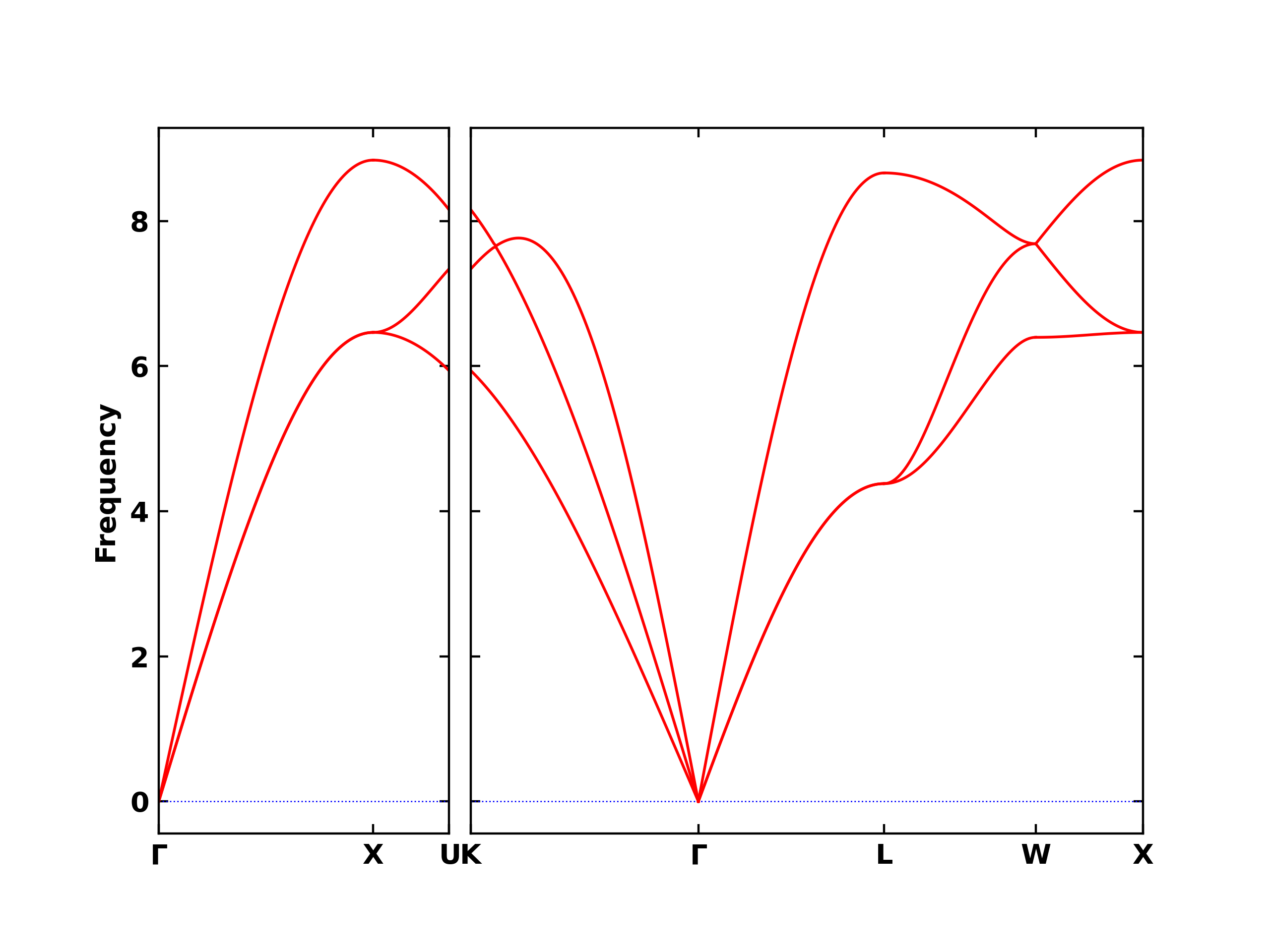
Band structure plot and values
[14]:
print('keys of "band_structure":', results_dict['band_structure'].keys())
Image("band.png", width=600)
keys of "band_structure": dict_keys(['qpoints', 'distances', 'frequencies', 'eigenvectors', 'group_velocities'])
[14]:
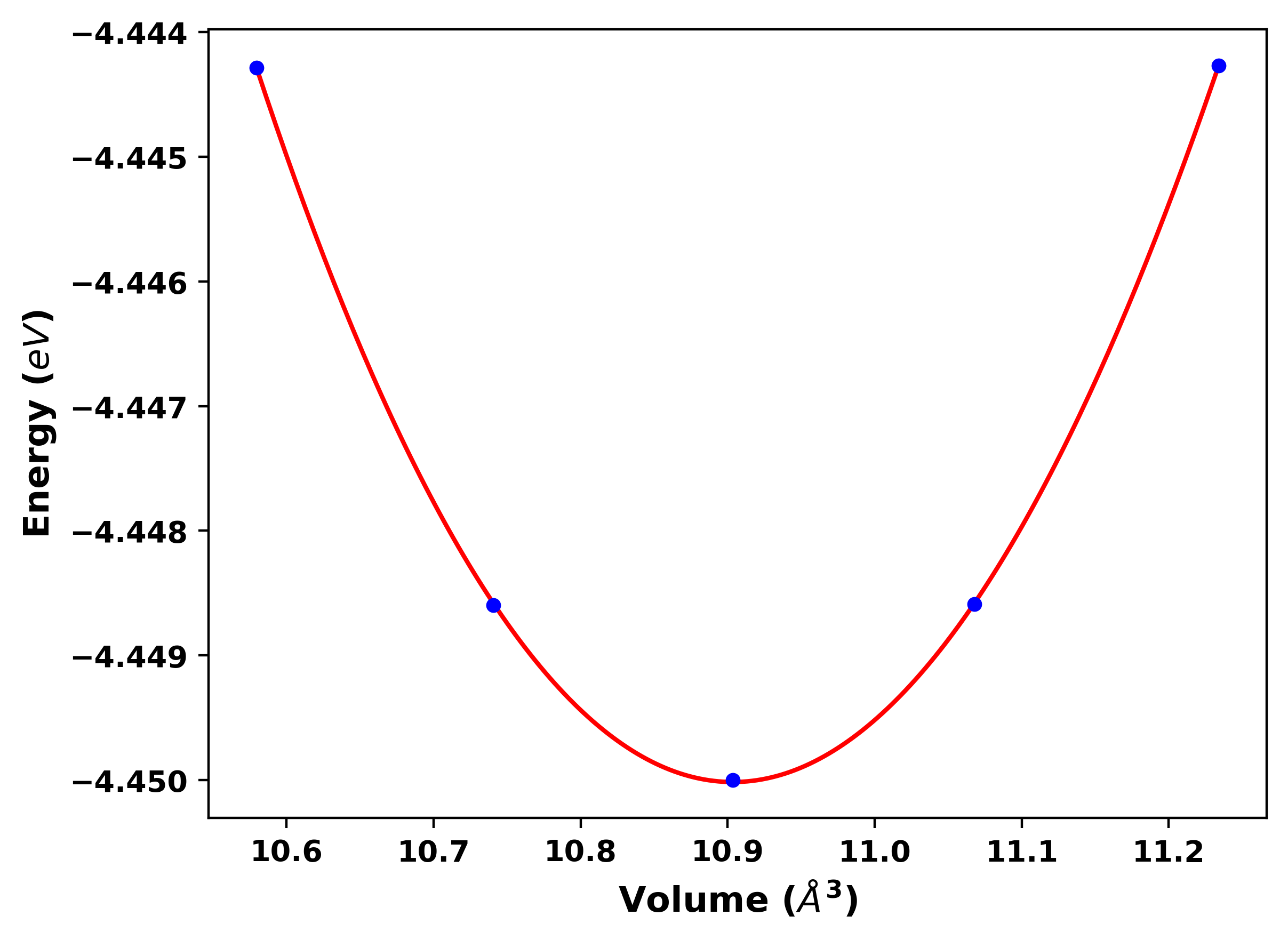
Volume versus energy scan plot and values
[15]:
print('keys of "volume_scan":',results_dict['volume_scan'].keys())
print('E0 =', uc.get_in_units(results_dict['E0'], 'eV'), 'eV')
print('B0 =', uc.get_in_units(results_dict['B0'], 'GPa'), 'GPa')
print('B0`=', uc.get_in_units(results_dict['B0prime'], 'GPa'), 'GPa')
print('V0 =', uc.get_in_units(results_dict['V0'], 'Å^3'), 'Å^3')
Image("bulk_modulus.png", width=600)
keys of "volume_scan": dict_keys(['volume', 'strain', 'energy'])
E0 = -4.450015536334154 eV
B0 = 187.29046746993 GPa
B0`= 137.80052380494985 GPa
V0 = 10.90348147775658 Å^3
[15]:
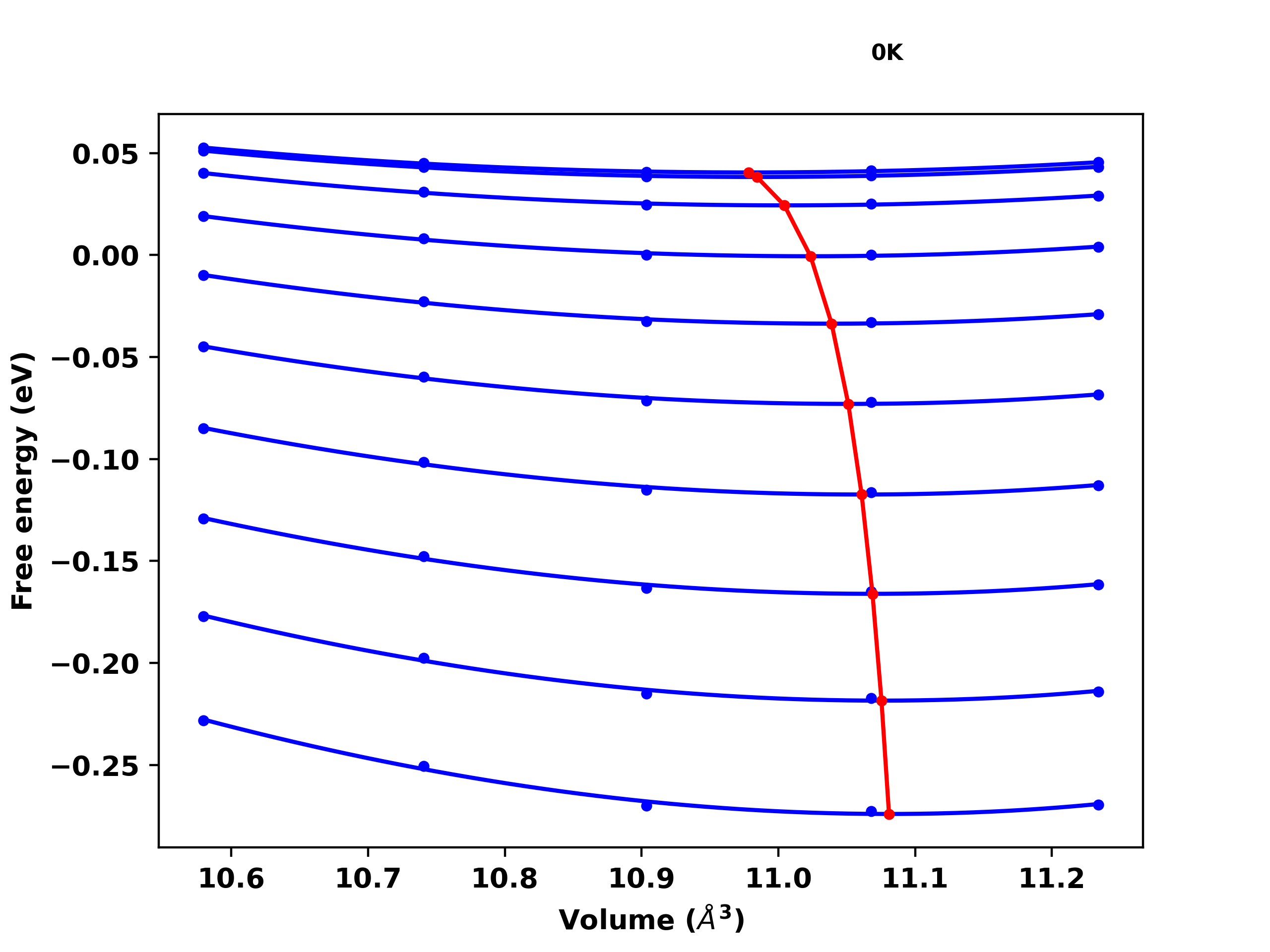
Helmholtz free energy versus volume plot
[16]:
Image("helmholtz_volume.png", width=600)
[16]:
Density of states
[17]:
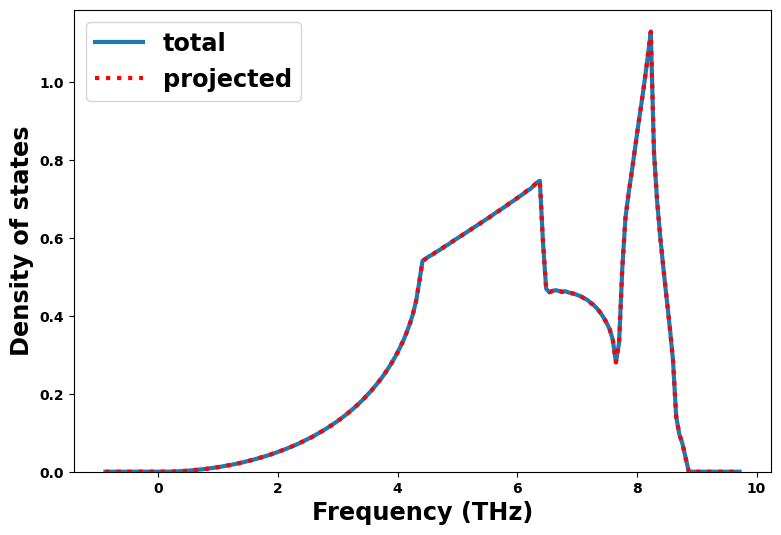
dos = results_dict['density_of_states']
fig = plt.figure(figsize=(9,6))
frequency = uc.get_in_units(dos['frequency'], 'THz')
plt.plot(frequency, dos['total_dos'], '-', lw=3, label='total')
for projected in dos['projected_dos']:
plt.plot(frequency, projected, 'r:', lw=3, label='projected')
plt.xlabel('Frequency (THz)', size='xx-large')
plt.ylabel('Density of states', size='xx-large')
plt.legend(loc=2, fontsize='xx-large')
plt.ylim(0.0, None)
plt.show()
Thermal properties - pull out temperature
[18]:
results_dict['thermal_properties'].keys()
thermal = results_dict['thermal_properties']
temperature = thermal['temperature']
Helmholtz and Gibbs free energies versus temperature
[19]:
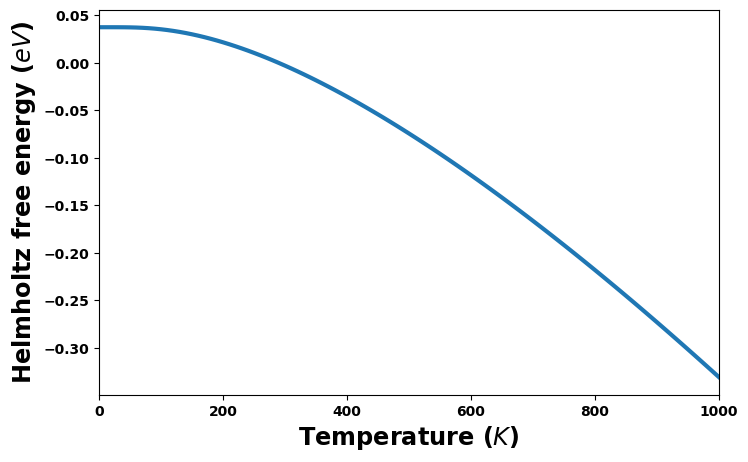
energy_unit = 'eV'
#energy_unit = 'kJ/mol'
fig = plt.figure(figsize=(8,5))
helmholtz = uc.get_in_units(thermal['Helmholtz'], energy_unit)
plt.plot(temperature, helmholtz, '-', lw=3)
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Helmholtz free energy (${energy_unit}$)', size='xx-large')
plt.show()
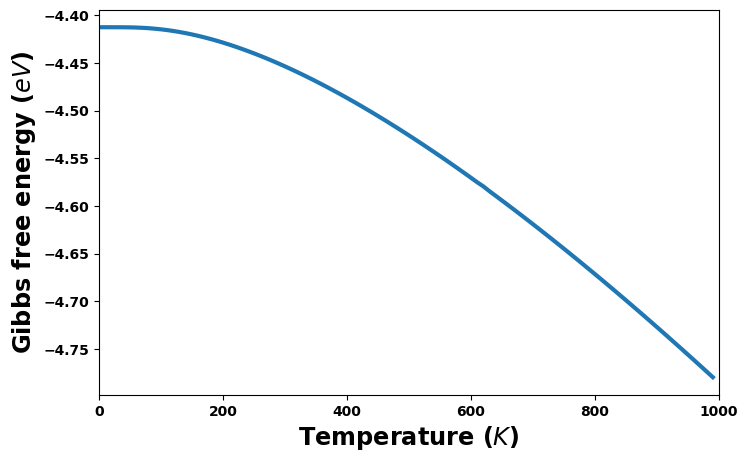
fig = plt.figure(figsize=(8,5))
gibbs = uc.get_in_units(thermal['Gibbs'], energy_unit)
plt.plot(temperature, gibbs, '-', lw=3)
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Gibbs free energy (${energy_unit}$)', size='xx-large')
plt.show()
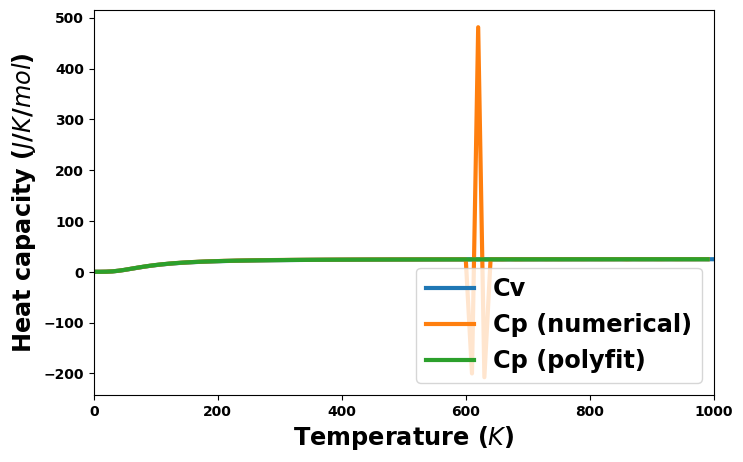
Entropy and heat capacity versus temperature
[20]:
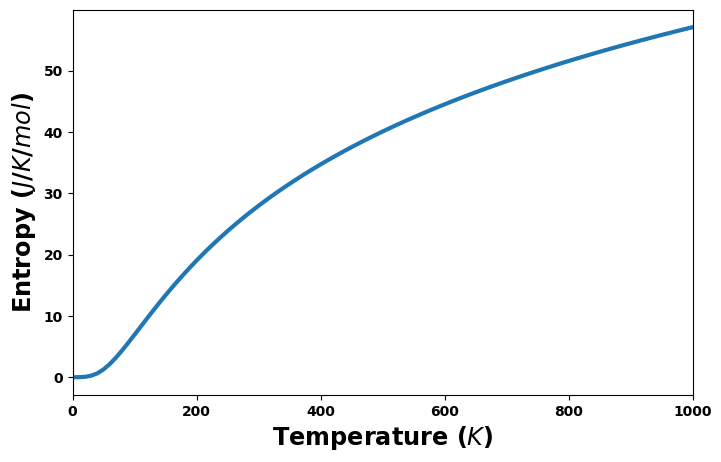
#entropy_unit = 'eV/K'
entropy_unit = 'J/K/mol'
fig = plt.figure(figsize=(8,5))
entropy = uc.get_in_units(thermal['entropy'], entropy_unit)
plt.plot(temperature, entropy, '-', lw=3)
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Entropy (${entropy_unit}$)', size='xx-large')
plt.show()
fig = plt.figure(figsize=(8,5))
heat_capacity_v = uc.get_in_units(thermal['heat_capacity_v'], entropy_unit)
heat_capacity_p_numerical = uc.get_in_units(thermal['heat_capacity_p_numerical'], entropy_unit)
heat_capacity_p_polyfit = uc.get_in_units(thermal['heat_capacity_p_polyfit'], entropy_unit)
plt.plot(temperature, heat_capacity_v, '-', lw=3, label='Cv')
plt.plot(temperature, heat_capacity_p_numerical, '-', lw=3, label='Cp (numerical)')
plt.plot(temperature, heat_capacity_p_polyfit, '-', lw=3, label='Cp (polyfit)')
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Heat capacity (${entropy_unit}$)', size='xx-large')
plt.legend(loc=4, fontsize='xx-large')
plt.show()
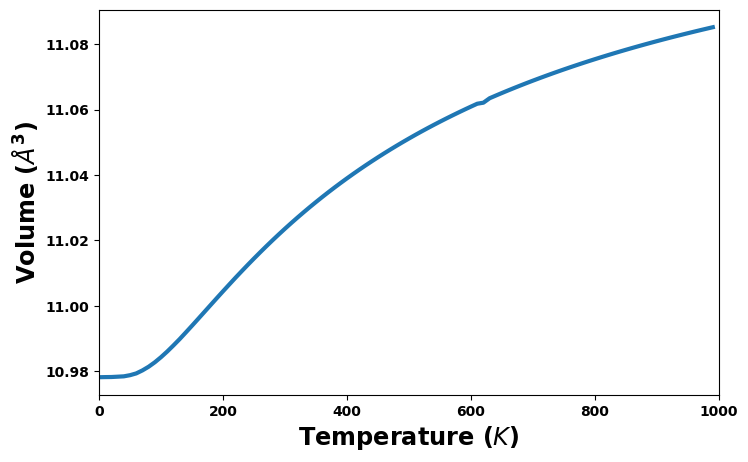
Volume versus temperature
[21]:
volume_unit = 'Å^3'
#volume_unit = 'nm^3'
fig = plt.figure(figsize=(8,5))
volume = uc.get_in_units(thermal['volume'], volume_unit)
plt.plot(temperature, volume, '-', lw=3)
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Volume (${volume_unit}$)', size='xx-large')
plt.show()
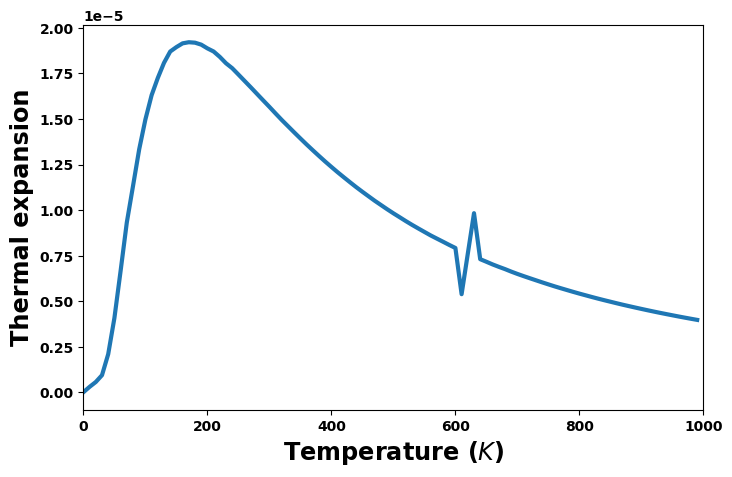
Thermal expansion versus temperature
[22]:
fig = plt.figure(figsize=(8,5))
expansion = thermal['thermal_expansion']
plt.plot(temperature, expansion, '-', lw=3)
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Thermal expansion', size='xx-large')
plt.show()
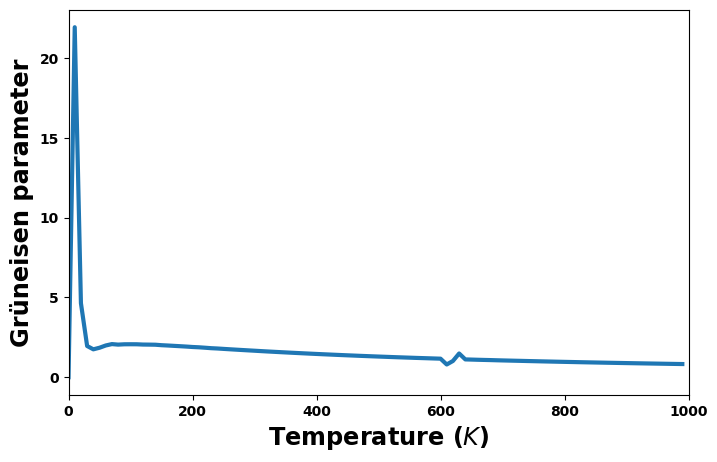
Grüneisen parameter versus temperature
[23]:
fig = plt.figure(figsize=(8,5))
gruneisen = thermal['gruneisen']
plt.plot(temperature, gruneisen, '-', lw=3)
plt.xlabel('Temperature ($K$)', size='xx-large')
plt.xlim(0, 1000)
plt.ylabel(f'Grüneisen parameter', size='xx-large')
plt.show()