stacking_fault_map_2D - Methodology and code
Python imports
[1]:
# Standard library imports
from pathlib import Path
import shutil
import datetime
from copy import deepcopy
from math import floor
from typing import Optional, Tuple, Union
# http://www.numpy.org/
import numpy as np
# https://ipython.org/
from IPython.display import display, Markdown
# https://github.com/usnistgov/atomman
import atomman as am
import atomman.lammps as lmp
import atomman.unitconvert as uc
from atomman.tools import filltemplate
# https://github.com/usnistgov/iprPy
import iprPy
from iprPy.tools import read_calc_file
import matplotlib.pyplot as plt
print('Notebook last executed on', datetime.date.today(), 'using iprPy version', iprPy.__version__)
Notebook last executed on 2023-07-31 using iprPy version 0.11.6
1. Load calculation and view description
1.1. Load the calculation
[2]:
# Load the calculation being demoed
calculation = iprPy.load_calculation('stacking_fault_map_2D')
1.2. Display calculation description and theory
[3]:
# Display main docs and theory
display(Markdown(calculation.maindoc))
display(Markdown(calculation.theorydoc))
stacking_fault_map_2D calculation style
Lucas M. Hale, lucas.hale@nist.gov, Materials Science and Engineering Division, NIST.
Introduction
The stacking_fault_map_2D calculation style evaluates the full 2D generalized stacking fault map for an array of shifts along a specified crystallographic plane. A regular grid of points is established and the generalized stacking fault energy is evaluated at each.
Version notes
2018-07-09: Notebook added.
2019-07-30: Description updated and small changes due to iprPy version.
2020-05-22: Version 0.10 update - potentials now loaded from database.
2020-09-22: Calculation updated to use atomman.defect.StackingFault class. Setup and parameter definition streamlined.
2022-03-11: Notebook updated to reflect version 0.11.
Additional dependencies
Disclaimers
The system’s dimension perpendicular to the fault plane should be large to minimize the interaction of the free surface and the stacking fault.
Method and Theory
First, an initial system is generated. This is accomplished using atomman.defect.StackingFault, which
Starts with a unit cell system.
Generates a transformed system by rotating the unit cell such that the new system’s box vectors correspond to crystallographic directions, and filled in with atoms to remain a perfect bulk cell when the three boundaries are periodic.
All atoms are shifted by a fractional amount of the box vectors if needed.
A supercell system is constructed by combining multiple replicas of the transformed system.
The system is then cut by making one of the box boundaries non-periodic. A limitation placed on the calculation is that the normal to the cut plane must correspond to one of the three Cartesian (\(x\), \(y\), or \(z\)) axes. If true, then of the system’s three box vectors (\(\vec{a}\), \(\vec{b}\), and \(\vec{c}\)), two will be parallel to the plane, and the third will not. The non-parallel box vector is called the cutboxvector, and for LAMMPS compatible systems, the following conditions can be used to check the system’s compatibility:
cutboxvector = ‘c’: all systems allowed.
cutboxvector = ‘b’: the system’s yz tilt must be zero.
cutboxvector = ‘a’: the system’s xy and xz tilts must be zero.
A LAMMPS simulation performs an energy/force minimization on the system where the atoms are confined to only relax along the Cartesian direction normal to the cut plane.
A mathematical fault plane parallel to the cut plane is defined in the middle of the system. A generalized stacking fault system can then be created by shifting all atoms on one side of the fault plane by a vector, \(\vec{s}\). The shifted system is then relaxed using the same confined energy/force minimization used on the non-shifted system. The generalized stacking fault energy, \(\gamma\), can then be computed by comparing the total energy of the system, \(E_{total}\), before and after \(\vec{s}\) is applied
where \(A\) is the area of the fault plane, which can be computed using the two box vectors, \(\vec{a_1}\) and \(\vec{a_2}\), that are not the cutboxvector.
Additionally, the relaxation normal to the glide plane is characterized using the center of mass of the atoms above and below the cut plane. Notably, the component of the center of mass normal to the glide/cut plane is calculated for the two halves of the the system, and the difference is computed
The relaxation normal is then taken as the change in the center of mass difference after the shift is applied.
The stacking_fault_map_2D calculation evaluates both \(\gamma\) and \(\Delta\delta\) for a complete 2D grid of \(\vec{s}\) values. The grid is built by taking fractional steps along two vectors parallel to the shift plane.
2. Define calculation functions and generate files
This section defines the calculation functions and associated resource files exactly as they exist inside the iprPy package. This allows for the code used to be directly visible and modifiable by anyone looking to see how it works.
2.1. stackingfaultmap()
This is the primary function for the calculation. The version of this function built in iprPy can be accessed by calling the calc() method of an object of the associated calculation class.
[4]:
def stackingfaultmap(lammps_command: str,
ucell: am.System,
potential: lmp.Potential,
hkl: Union[list, np.ndarray],
mpi_command: Optional[str] = None,
sizemults: Union[list, tuple, None] = None,
minwidth: float = None,
even: bool = False,
a1vect_uvw: Union[list, np.ndarray, None] = None,
a2vect_uvw: Union[list, np.ndarray, None] = None,
conventional_setting: str = 'p',
cutboxvector: str = 'c',
faultpos_rel: Optional[float] = None,
faultpos_cart: Optional[float] = None,
num_a1: int = 10,
num_a2: int = 10,
atomshift: Union[list, np.ndarray, None] = None,
shiftindex: Optional[int] = None,
etol: float = 0.0,
ftol: float = 0.0,
maxiter: int = 10000,
maxeval: int = 100000,
dmax: float = uc.set_in_units(0.01, 'angstrom')) -> dict:
"""
Computes a generalized stacking fault map for shifts along a regular 2D
grid.
Parameters
----------
lammps_command :str
Command for running LAMMPS.
ucell : atomman.System
The crystal unit cell to use as the basis of the stacking fault
configurations.
potential : atomman.lammps.Potential
The LAMMPS implemented potential to use.
hkl : array-like object
The Miller(-Bravais) crystal fault plane relative to ucell.
mpi_command : str, optional
The MPI command for running LAMMPS in parallel. If not given, LAMMPS
will run serially.
sizemults : list or tuple, optional
The three System.supersize multipliers [a_mult, b_mult, c_mult] to use on the
rotated cell to build the final system. Note that the cutboxvector sizemult
must be an integer and not a tuple. Default value is [1, 1, 1].
minwidth : float, optional
If given, the sizemult along the cutboxvector will be selected such that the
width of the resulting final system in that direction will be at least this
value. If both sizemults and minwidth are given, then the larger of the two
in the cutboxvector direction will be used.
even : bool, optional
A True value means that the sizemult for cutboxvector will be made an even
number by adding 1 if it is odd. Default value is False.
a1vect_uvw : array-like object, optional
The crystal vector to use for one of the two shifting vectors. If
not given, will be set to the shortest in-plane lattice vector.
a2vect_uvw : array-like object, optional
The crystal vector to use for one of the two shifting vectors. If
not given, will be set to the shortest in-plane lattice vector not
parallel to a1vect_uvw.
conventional_setting : str, optional
Allows for rotations of a primitive unit cell to be determined from
(hkl) indices specified relative to a conventional unit cell. Allowed
settings: 'p' for primitive (no conversion), 'f' for face-centered,
'i' for body-centered, and 'a', 'b', or 'c' for side-centered. Default
behavior is to perform no conversion, i.e. take (hkl) relative to the
given ucell.
cutboxvector : str, optional
Indicates which of the three system box vectors, 'a', 'b', or 'c', to
cut with a non-periodic boundary (default is 'c').
faultpos_rel : float, optional
The position to place the slip plane within the system given as a
relative coordinate along the out-of-plane direction. faultpos_rel
and faultpos_cart cannot both be given. Default value is 0.5 if
faultpos_cart is also not given.
faultpos_cart : float, optional
The position to place the slip plane within the system given as a
Cartesian coordinate along the out-of-plane direction. faultpos_rel
and faultpos_cart cannot both be given.
num_a1 : int, optional
The number of fractional coordinates to evaluate along a1vect_uvw.
Default value is 10.
num_a2 : int, optional
The number of fractional coordinates to evaluate along a2vect_uvw.
Default value is 10.
atomshift : array-like object, optional
A Cartesian vector shift to apply to all atoms. Can be used to shift
atoms perpendicular to the fault plane to allow different termination
planes to be cut. Cannot be given with shiftindex.
shiftindex : int, optional
Allows for selection of different termination planes based on the
preferred shift values determined by the underlying fault generation.
Cannot be given with atomshift. If neither atomshift nor shiftindex
given, then shiftindex will be set to 0.
etol : float, optional
The energy tolerance for the structure minimization. This value is
unitless. (Default is 0.0).
ftol : float, optional
The force tolerance for the structure minimization. This value is in
units of force. (Default is 0.0).
maxiter : int, optional
The maximum number of minimization iterations to use (default is
10000).
maxeval : int, optional
The maximum number of minimization evaluations to use (default is
100000).
dmax : float, optional
The maximum distance in length units that any atom is allowed to relax
in any direction during a single minimization iteration (default is
0.01 Angstroms).
Returns
-------
dict
Dictionary of results consisting of keys:
- **'A_fault'** (*float*) - The area of the fault surface.
- **'gamma'** (*atomman.defect.GammaSurface*) - A gamma surface
plotting object.
"""
# Construct stacking fault configuration generator
gsf_gen = am.defect.StackingFault(hkl, ucell, cutboxvector=cutboxvector,
a1vect_uvw=a1vect_uvw, a2vect_uvw=a2vect_uvw,
conventional_setting=conventional_setting)
# Check shift parameters
if shiftindex is not None:
assert atomshift is None, 'shiftindex and atomshift cannot both be given'
atomshift = gsf_gen.shifts[shiftindex]
elif atomshift is None:
atomshift = gsf_gen.shifts[0]
# Generate the free surface (zero-shift) configuration
gsf_gen.surface(shift=atomshift, minwidth=minwidth, sizemults=sizemults,
even=even, faultpos_rel=faultpos_rel,
faultpos_cart=faultpos_cart)
abovefault = gsf_gen.abovefault
cutindex = gsf_gen.cutindex
A_fault = gsf_gen.surfacearea
# Identify lammps_date version
lammps_date = lmp.checkversion(lammps_command)['date']
# Define lists
a1vals = []
a2vals = []
E_totals = []
disps = []
# Loop over all shift combinations
for a1, a2, sfsystem in gsf_gen.iterfaultmap(num_a1=num_a1, num_a2=num_a2):
a1vals.append(a1)
a2vals.append(a2)
# Evaluate the system at the shift
sim_directory = Path('a%.10f-b%.10f' % (a1, a2))
relax = stackingfaultrelax(lammps_command, sfsystem, potential,
mpi_command=mpi_command,
sim_directory=sim_directory,
cutboxvector=cutboxvector,
etol=etol, ftol=ftol, maxiter=maxiter,
maxeval=maxeval, dmax=dmax,
lammps_date=lammps_date)
# Extract terms
E_totals.append(relax['E_total'])
pos = relax['system'].atoms.pos
disps.append(pos[abovefault, cutindex].mean()
- pos[~abovefault, cutindex].mean())
E_totals = np.array(E_totals)
disps = np.array(disps)
# Get zeroshift values
E_total_0 = E_totals[0]
disp_0 = disps[0]
# Compute the stacking fault energies
E_gsfs = (E_totals - E_total_0) / A_fault
# Compute the change in displacement normal to fault plane
delta_disps = disps - disp_0
results_dict = {}
results_dict['A_fault'] = A_fault
results_dict['gamma'] = am.defect.GammaSurface(a1vect = gsf_gen.a1vect_uvw,
a2vect = gsf_gen.a2vect_uvw,
box = gsf_gen.ucell.box,
a1 = a1vals,
a2 = a2vals,
E_gsf = E_gsfs,
delta = delta_disps)
return results_dict
2.2. stackingfaultrelax()
[5]:
def stackingfaultrelax(lammps_command: str,
system: am.System,
potential: lmp.Potential,
mpi_command: Optional[str] = None,
sim_directory: Optional[str] = None,
cutboxvector: str = 'c',
etol: float = 0.0,
ftol: float = 0.0,
maxiter: int = 10000,
maxeval: int = 100000,
dmax: float = uc.set_in_units(0.01, 'angstrom'),
lammps_date: Optional[datetime.date] = None) -> dict:
"""
Perform a stacking fault relaxation simulation for a single faultshift.
Parameters
----------
lammps_command :str
Command for running LAMMPS.
system : atomman.System
The system containing a stacking fault.
potential : atomman.lammps.Potential
The LAMMPS implemented potential to use.
mpi_command : str, optional
The MPI command for running LAMMPS in parallel. If not given, LAMMPS
will run serially.
sim_directory : str, optional
The path to the directory to perform the simulation in. If not
given, will use the current working directory.
cutboxvector : str, optional
Indicates which of the three system box vectors, 'a', 'b', or 'c', has
the non-periodic boundary (default is 'c'). Fault plane normal is
defined by the cross of the other two box vectors.
etol : float, optional
The energy tolerance for the structure minimization. This value is
unitless. (Default is 0.0).
ftol : float, optional
The force tolerance for the structure minimization. This value is in
units of force. (Default is 0.0).
maxiter : int, optional
The maximum number of minimization iterations to use (default is
10000).
maxeval : int, optional
The maximum number of minimization evaluations to use (default is
100000).
dmax : float, optional
The maximum distance in length units that any atom is allowed to relax
in any direction during a single minimization iteration (default is
0.01 Angstroms).
lammps_date : datetime.date or None, optional
The date version of the LAMMPS executable. If None, will be identified
from the lammps_command (default is None).
Returns
-------
dict
Dictionary of results consisting of keys:
- **'logfile'** (*str*) - The filename of the LAMMPS log file.
- **'dumpfile'** (*str*) - The filename of the LAMMPS dump file
of the relaxed system.
- **'system'** (*atomman.System*) - The relaxed system.
- **'E_total'** (*float*) - The total potential energy of the relaxed
system.
Raises
------
ValueError
For invalid cutboxvectors.
"""
# Give correct LAMMPS fix setforce command
if cutboxvector == 'a':
fix_cut_setforce = 'fix cut all setforce NULL 0 0'
elif cutboxvector == 'b':
fix_cut_setforce = 'fix cut all setforce 0 NULL 0'
elif cutboxvector == 'c':
fix_cut_setforce = 'fix cut all setforce 0 0 NULL'
else:
raise ValueError('Invalid cutboxvector')
if sim_directory is not None:
# Create sim_directory if it doesn't exist
sim_directory = Path(sim_directory)
if not sim_directory.is_dir():
sim_directory.mkdir()
sim_directory = sim_directory.as_posix()+'/'
else:
# Set sim_directory if is None
sim_directory = ''
# Get lammps units
lammps_units = lmp.style.unit(potential.units)
#Get lammps version date
if lammps_date is None:
lammps_date = lmp.checkversion(lammps_command)['date']
# Define lammps variables
lammps_variables = {}
system_info = system.dump('atom_data',
f=Path(sim_directory, 'system.dat').as_posix(),
potential=potential)
lammps_variables['atomman_system_pair_info'] = system_info
lammps_variables['fix_cut_setforce'] = fix_cut_setforce
lammps_variables['sim_directory'] = sim_directory
lammps_variables['etol'] = etol
lammps_variables['ftol'] = uc.get_in_units(ftol, lammps_units['force'])
lammps_variables['maxiter'] = maxiter
lammps_variables['maxeval'] = maxeval
lammps_variables['dmax'] = uc.get_in_units(dmax, lammps_units['length'])
# Set dump_modify format based on dump_modify_version
if lammps_date < datetime.date(2016, 8, 3):
lammps_variables['dump_modify_format'] = '"%i %i %.13e %.13e %.13e %.13e"'
else:
lammps_variables['dump_modify_format'] = 'float %.13e'
# Write lammps input script
lammps_script = Path(sim_directory, 'sfmin.in')
template = read_calc_file('iprPy.calculation.stacking_fault_map_2D',
'sfmin.template')
with open(lammps_script, 'w') as f:
f.write(filltemplate(template, lammps_variables, '<', '>'))
# Run LAMMPS
output = lmp.run(lammps_command, script_name=lammps_script.as_posix(),
mpi_command=mpi_command,
logfile=Path(sim_directory, 'log.lammps').as_posix())
# Extract output values
thermo = output.simulations[-1]['thermo']
logfile = Path(sim_directory, 'log.lammps').as_posix()
dumpfile = Path(sim_directory, '%i.dump' % thermo.Step.values[-1]).as_posix()
E_total = uc.set_in_units(thermo.PotEng.values[-1],
lammps_units['energy'])
# Load relaxed system
system = am.load('atom_dump', dumpfile, symbols=system.symbols)
# Return results
results_dict = {}
results_dict['logfile'] = logfile
results_dict['dumpfile'] = dumpfile
results_dict['system'] = system
results_dict['E_total'] = E_total
return results_dict
2.3. sfmin.template file
[6]:
with open('sfmin.template', 'w') as f:
f.write("""#LAMMPS input script that performs an energy minimization
#for a system with a stacking fault
box tilt large
<atomman_system_pair_info>
<fix_cut_setforce>
thermo_style custom step lx ly lz pxx pyy pzz pe
thermo_modify format float %.13e
compute peatom all pe/atom
min_modify dmax <dmax>
dump dumpit all custom <maxeval> <sim_directory>*.dump id type x y z c_peatom
dump_modify dumpit format <dump_modify_format>
minimize <etol> <ftol> <maxiter> <maxeval>""")
3. Specify input parameters
3.1. System-specific paths
lammps_command is the LAMMPS command to use (required).
mpi_command MPI command for running LAMMPS in parallel. A value of None will run simulations serially.
[7]:
lammps_command = 'lmp'
mpi_command = None
# Optional: check that LAMMPS works and show its version
print(f'LAMMPS version = {am.lammps.checkversion(lammps_command)["version"]}')
LAMMPS version = 15 Sep 2022
3.2. Interatomic potential
potential_name gives the name of the potential_LAMMPS reference record in the iprPy library to use for the calculation.
potential is an atomman.lammps.Potential object (required).
[8]:
potential_name = '1999--Mishin-Y--Ni--LAMMPS--ipr1'
# Retrieve potential and parameter file(s) using atomman
potential = am.load_lammps_potential(id=potential_name, getfiles=True)
3.3. Initial unit cell system
ucell is an atomman.System representing a fundamental unit cell of the system (required). Here, this is generated using the load parameters and symbols.
[9]:
# Create ucell by loading prototype record
ucell = am.load('crystal', potential=potential, family='A1--Cu--fcc')
print(ucell)
avect = [ 3.520, 0.000, 0.000]
bvect = [ 0.000, 3.520, 0.000]
cvect = [ 0.000, 0.000, 3.520]
origin = [ 0.000, 0.000, 0.000]
natoms = 4
natypes = 1
symbols = ('Ni',)
pbc = [ True True True]
per-atom properties = ['atype', 'pos']
id atype pos[0] pos[1] pos[2]
0 1 0.000 0.000 0.000
1 1 0.000 1.760 1.760
2 1 1.760 0.000 1.760
3 1 1.760 1.760 0.000
3.4. Defect parameters
hkl gives the Miller (hkl) or Miller-Bravais (hkil) plane to create the free surface on.
cutboxvector specifies which of the three box vectors (‘a’, ‘b’, or ‘c’) is to be made non-periodic to create the free surface.
shiftindex can be used for complex crystals to specify different termination planes.
a1vect_uvw, a2vect_uvw specify two non-parallel Miller crystal vectors within the fault plane corresponding to full planar shifts from one perfect crystal configuration to another.
num_a1, num_a2 specify how many measurements to make along a1vect_uvw, a2vect_uvw respectively.
[10]:
hkl = [1, 1, 1]
cutboxvector = 'c'
shiftindex = 0
a1vect_uvw = [ 0.0,-0.5, 0.5]
a2vect_uvw = [ 0.5,-0.5, 0.0]
num_a1 = 30
num_a2 = 30
3.5. System modifications
sizemults list of three integers specifying how many times the ucell vectors of \(a\), \(b\) and \(c\) are replicated in creating system.
minwidth specifies a minimum width that the system should be along the cutboxvector direction. The given sizemult in that direction will be increased if needed to ensure that the system is at least this wide.
[11]:
sizemults = [5, 5, 10]
minwidth = uc.set_in_units(0.0, 'angstrom')
3.5. Calculation-specific parameters
energytolerance is the energy tolerance to use during the minimizations. This is unitless.
forcetolerance is the force tolerance to use during the minimizations. This is in energy/length units.
maxiterations is the maximum number of minimization iterations to use.
maxevaluations is the maximum number of minimization evaluations to use.
maxatommotion is the largest distance that an atom is allowed to move during a minimization iteration. This is in length units.
[12]:
energytolerance = 1e-8
forcetolerance = uc.set_in_units(0.0, 'eV/angstrom')
maxiterations = 10000
maxevaluations = 100000
maxatommotion = uc.set_in_units(0.01, 'angstrom')
4. Run calculation and view results
4.1. Run calculation
All primary calculation method functions take a series of inputs and return a dictionary of outputs.
[13]:
results_dict = stackingfaultmap(lammps_command, ucell, potential, hkl,
mpi_command = mpi_command,
sizemults = sizemults,
minwidth = minwidth,
a1vect_uvw = a1vect_uvw,
a2vect_uvw = a2vect_uvw,
cutboxvector = cutboxvector,
shiftindex = shiftindex,
num_a1 = num_a1,
num_a2 = num_a2,
etol = energytolerance,
ftol = forcetolerance,
maxiter = maxiterations,
maxeval = maxevaluations,
dmax = maxatommotion)
print(results_dict.keys())
dict_keys(['A_fault', 'gamma'])
4.2. Report results
Values returned in the results_dict:
‘A_fault’ (float) - The area of the fault surface.
‘gamma’ (atomman.defect.GammaSurface) - A gamma surface plotting object.
[14]:
length_unit = 'nm'
area_unit = 'nm^2'
energy_unit = 'eV'
energyperarea_unit = 'mJ/m^2'
[15]:
print('A_fault =', uc.get_in_units(results_dict['A_fault'], area_unit), area_unit)
A_fault = 5.365198866947918 nm^2
[16]:
gamma = results_dict['gamma']
print(gamma.a1vect)
print(gamma.a2vect)
[ 0. -0.5 0.5]
[ 0.5 -0.5 0. ]
[17]:
# Save gamma as data model
with open('gamma.json', 'w') as f:
gamma.model().json(fp=f, indent=4)
[18]:
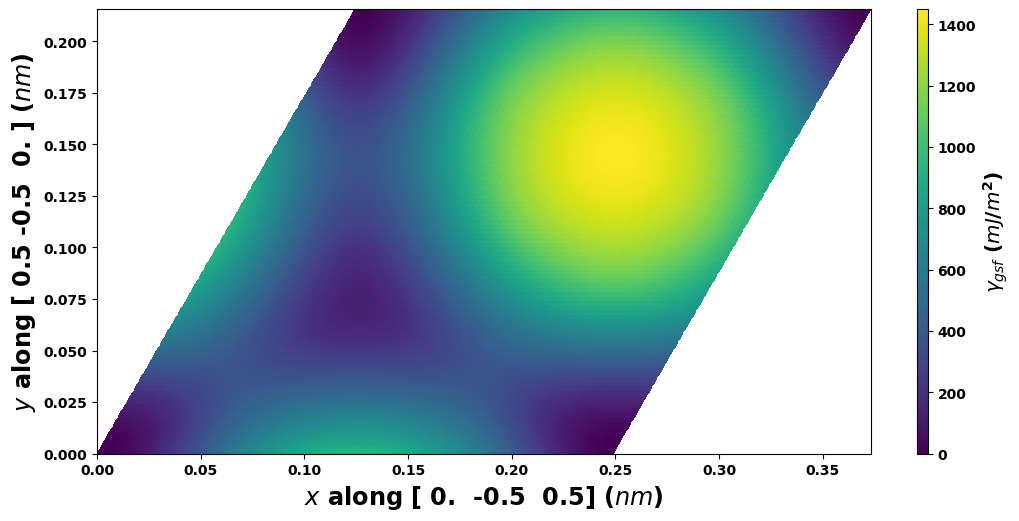
# Plot with calculation a1vect, a2vect
gamma.E_gsf_surface_plot(length_unit=length_unit,
energyperarea_unit=energyperarea_unit)
plt.show()
[19]:
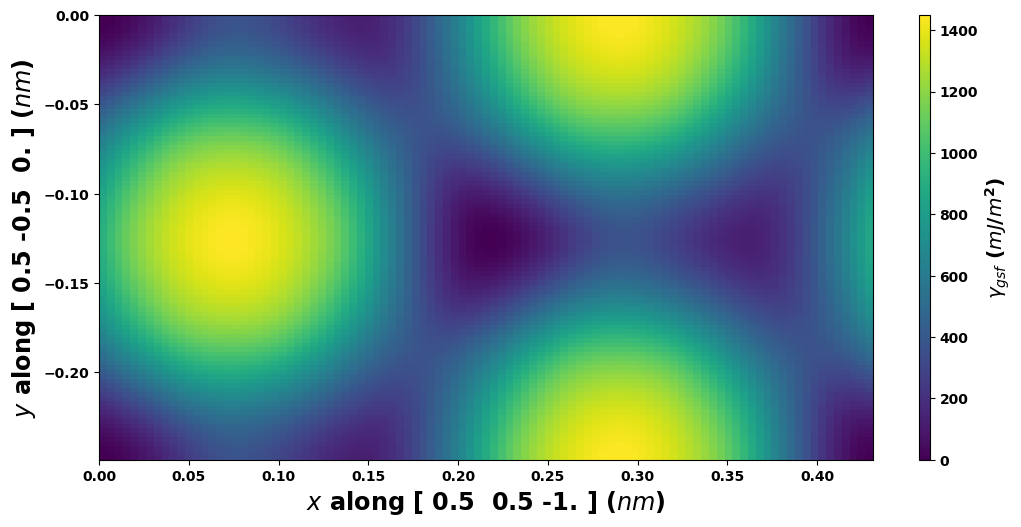
# Plot with standard A1--fcc--111sf a1vect, a2vect
gamma.E_gsf_surface_plot(a1vect=[0.5, 0.5, -1],
a2vect=gamma.a2vect,
length_unit=length_unit,
energyperarea_unit=energyperarea_unit)
plt.show()
[20]:
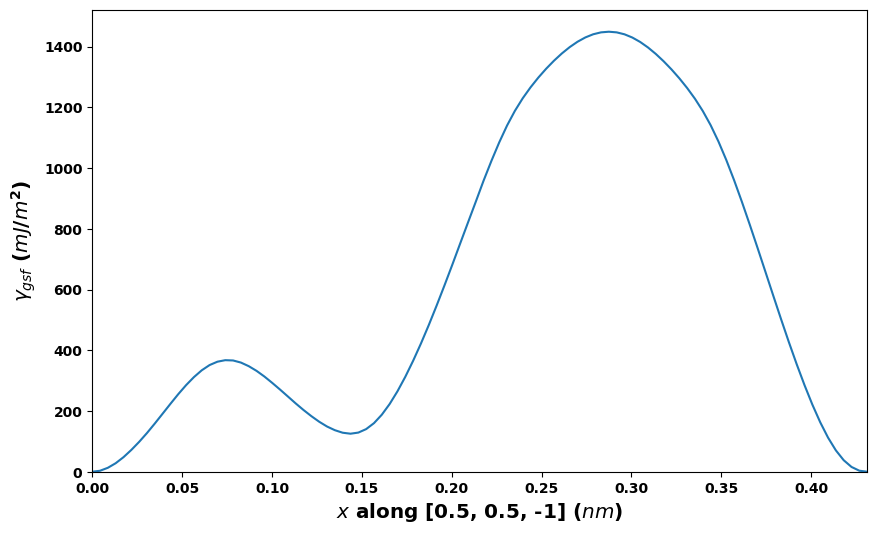
# Standard 1D [11-2](111) fcc path
gamma.E_gsf_line_plot(vect=[0.5, 0.5, -1], length_unit=length_unit,
energyperarea_unit=energyperarea_unit)
plt.show()