OOF: Finite Element Analysis of Microstructures

valeria next up previous contents
Next: Graphics Drawers Up: Element Types and their Previous: zimmer and zimmer2   Contents

Subsections


valeria

This element was contributed by Valeria Cannillo. It is designed to fail (i.e. mutate) following the Weibull law:

\begin{displaymath} P_{fail}(\sigma, \Delta V; {\sigma_\circ} , m) = 1 - \exp \l... ...gma}{{\sigma_\circ}}\right)^m \frac{\Delta V}{V_\circ} \right] \end{displaymath} (4.2)

that correlates the probability of failure to the stress state $\sigma$ in a volume $\Delta V$ and to two Weibull parameters (a shape factor $m$ and a scale parameter ${\sigma_\circ}$). $V_\circ$ is the reference volume - the specimen volume for which the Weibull parameters were determined.

A failure probability $P_{fail}$ is computed in every element from Eq. (4.2), using the maximum principal stress as $\sigma$. Each element has an area $\Delta A$ that is used to determine the volume $\Delta V$ in Eq. (4.2) through the characteristic element thickness.

Each element is then randomly assigned a test probability $P_{test}$ from a uniform distribution in the interval $[0,1]$. The element fractures if

\begin{displaymath} P_{fail} > P_{test} \end{displaymath} (4.3)

The process of mutation is similar to that for the damage element (Section 4.5.10):

1. if Eq. (4.3) is favorable for cracking, the direction of the maximum principle stress is found

2. Modification of the stiffness matrix proceeds as in the damage element

Parameters

orientation
As with the damage element. this is meaningless.

thermoelastic coefficients
All thermoelastic coefficients for a undamaged element are isotropic.

weibull_m
The Weibull parameter 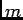$m$. [dimensionless]

weibull_s0
The Weibull parameter 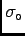${\sigma_\circ}$. [stress]

weibull_a0
The reference area 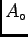$A_\circ$ (related to the reference volume 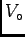$V_\circ$ through the characteristic element thickness) [area]

knockdown1
The factor which multiplies the rotated stiffness matrix's Czzz z component during a mutation. This should be a small number, if the element is really to be ``cracked''. [dimensionless]

knockdown2
The factor which multiplies the rotated stiffness matrix's remaining Cijkl components for at least one of ijkl=z during a mutation. [dimensionless]

only_once
If true, an element which has been damaged during one mutate command will not be damaged further on subsequent mutate commands. If false, the knockdown factors may be applied multiple times. Default: false

next up previous contents
Next: Graphics Drawers Up: Element Types and their Previous: zimmer and zimmer2   Contents
/* Send mail to the OOF Team *//* Go to the OOF Home Page */