OOF: Finite Element Analysis of Microstructures

griffith and griffith2 next up previous contents
Next: trigonalCrack Up: Element Types and their Previous: damage   Contents

Subsections


griffith and griffith2

These elements are designed to fail (i.e, mutate (Section 3.1.4)) under the Griffith criterion, which states that a crack will propagate when the total surface energy required to propagate the crack can be supplied by the elastic energy stored in the body:

\begin{displaymath} 2\ell\gamma < \frac12\int\sigma\epsilon dV, \end{displaymath} (4.1)

where $\ell$ is the crack length and $\gamma$ is the surface energy of the cracked interface. In OOF the element size is used to specify the characteristic crack length and the volume of integration is the element area (per unit depth). In other words, the elastic energy is assumed to come entirely from the cracking element.

Because elements in OOF can't actually crack, after mutating the elements reduce their moduli anisotropically to simulate a crack, and the amount of surface area generated by mutation has to be estimated. We take it to be the diameter of a circle with the same area as the element.

CAUTION: Neither griffith nor griffith2 is a fully correct implementation of the Griffith criterion. griffith mutates when the stored elastic energy before mutation is greater than the surface energy after mutation, which doesn't account for the fact that there is still some elastic energy left in the element after it mutates. griffith2 solves this problem partially by not including energy due to stress perpendicular to the surface.

The process of mutation is similar to that for the damage element (Section 4.5.10):

  1. The energy balance for cracking is computed.
  2. If the energy balance is favorable for cracking, the direction of the maximum principle stress is found.
  3. Modfication of the stiffness matrix proceeds as in the damage element (Section 4.5.10).

Parameters

orientation
As with the damage element, this is meaningless. See the explanation in Section 4.5.10. [degrees]

thermoelastic coefficients
All thermoelastic coefficients for a undamaged damage element are isotropic as described in section 4.5.1.

gamma
The energy per unit length of the crack surface. [stress/length]4.6

knockdown1
The factor which multiplies the rotated stiffness matrix's 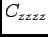$C_{zzzz}$ component during a mutation. This should be a small number, if the element is really to be ``cracked''. [dimensionless]

knockdown2
The factor which multiplies the rotated stiffness matrix's remaining $C_{ijkl}$ components for at least one of ijkl=z during a mutation. [dimensionless]

only_once
If true, an element which has been damaged during one mutate command will not be damaged further on subsequent mutate commands. If false, the knockdown factors may be applied multiple times. Default: false

next up previous contents
Next: trigonalCrack Up: Element Types and their Previous: damage   Contents
/* Send mail to the OOF Team *//* Go to the OOF Home Page */