OOF: Finite Element Analysis of Microstructures

isotropic

Next: empty Up: Element Types and their Previous: Element Types and their Contents

Subsections

Parameters

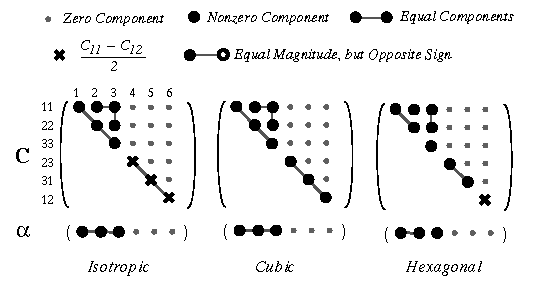
isotropic

An isotropic element has the same stiffness independent of the loading direction or the plane on which the load is applied.

According to Figure 4.2, there are two independent elastic constants. OOF uses the Young's modulus and the Poisson's ratio $\nu$ for the two input variables. In the case of plane stress, the $3\times3$ stiffness matrix is:

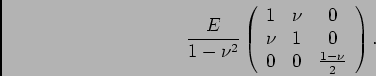
$\begin{displaymath} \frac{E}{1-\nu^2} \left( \begin{array}{ccc} 1 & \nu & 0\\ \nu & 1 & 0\\ 0 & 0 & \frac{1-\nu}{2} \end{array}\right). \end{displaymath}$

For plane strain, the stiffness matrix is:

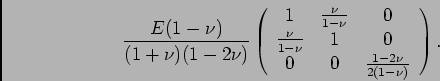
$\begin{displaymath} \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} \left( \begin{array}{ccc} 1... ...& 1 & 0\\ 0 & 0 & \frac{1-2\nu}{2(1-\nu)} \end{array}\right). \end{displaymath}$

Parameters

young: The Young's modulus 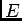[stress].
poisson: The Poisson's ratio 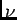$\nu$ [dimensionless].
alpha: The coefficient of thermal expansion [inverse temperature].

**Figure 4.2:** Symmetries of the stiffness matrix for Isotropic, Cubic and Hexagonal materials.

/* Send mail to the OOF Team *//* Go to the OOF Home Page */