µMAG Standard Problem #4 results

Disclaimer

Solution directory

• Comparisons
• G. Albuquerque, J. Miltat and A. Thiaville
• R. D. McMichael, M. J. Donahue, D. G. Porter, and J. Eicke
• Liliana Buda, Lucian Prejbeanu, Ursula Ebels and Kamel Ounadjela
• E. Martinez, L. Torres and L. Lopez-Diaz
• José L. Martins and Tania Rocha
• P.E. Roy and P. Svedlindh
• Massimiliano d’Aquino, Claudio Serpico, and Giovanni Miano
• Dmitri Berkov
• M. J. Donahue and D. G. Porter
• Rasmus Bjørk, E. B. Poulsen and A. R. Insinga

Submitted Solution: Rasmus Bjørk, E. B. Poulsen and A. R. Insinga

Date:

October 5th, 2021.

From:

Rasmus Bjørk, E. B. Poulsen and A. R. Insinga
Department of Energy Conversion and Storage, Technical University of Denmark, Denmark

Contact:

Rasmus Bjørk

We used the MagTense open source micromagnetic simulation framework to compute solutions to standard problem #4.

The spatial discretization subdivided the film into a collection of N rectangular prisms with edges parallel to the coordinate axes. (N = N_x × N_y × N_z), where in this specific problem we take N_x=160, N_y=40, N_z=1 in order to get cubic elements, as the film has a length four times its width. The film is assumed thin, and thus only resolved by a single point in the z-direction. The magnetization is assumed uniform within each cell.

The numerical details of the computation of the exchange and demagnetization field can be found in the references below. The exchange field has been computed by using a standard finite difference centered stencil. The correct Neumann boundary condition has been applied to the problem. The demagnetization field was computed using an analytically correct expression for the demagnetization field from prisms, as described in the references below. The time integration of the LLG equation is performed using an explicit Runge-Kutta (4,5) formula.

Results:

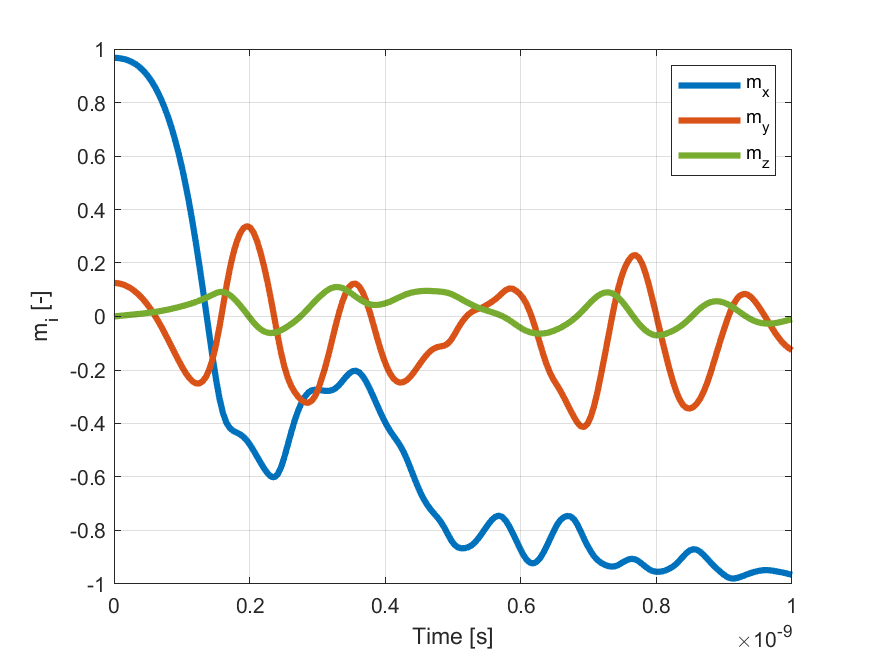
• Field applied: μ₀H= [-24.6,4.3,0.0] mT. The different components of the spatially averaged normalized magnetization as function of time is shown below up to t = 1 ns.
  
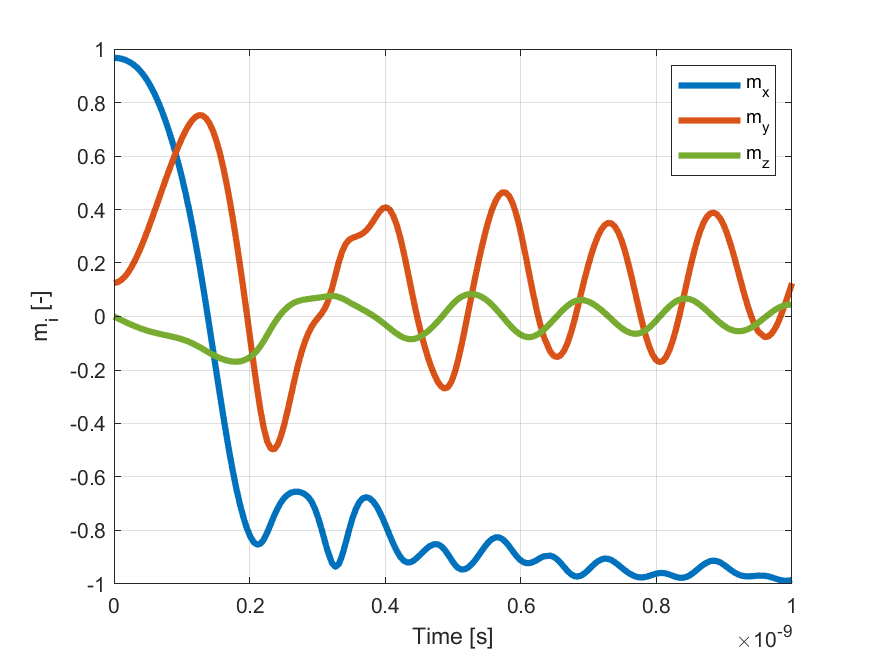
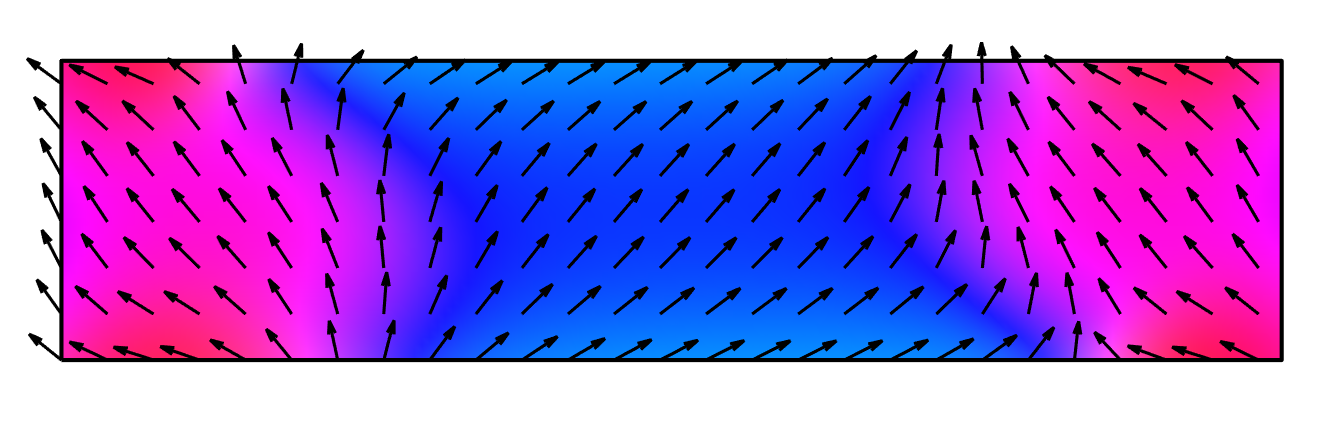
  We also shown an image of the magnetization when first crosses zero below, as well as an animated sequence of the time evolution of the magnetization. The number of arrows drawn has been reduced from the actual 160x40 simulation. The color indicate the direction of the magnetization as shown in the small legend.
  
  
  
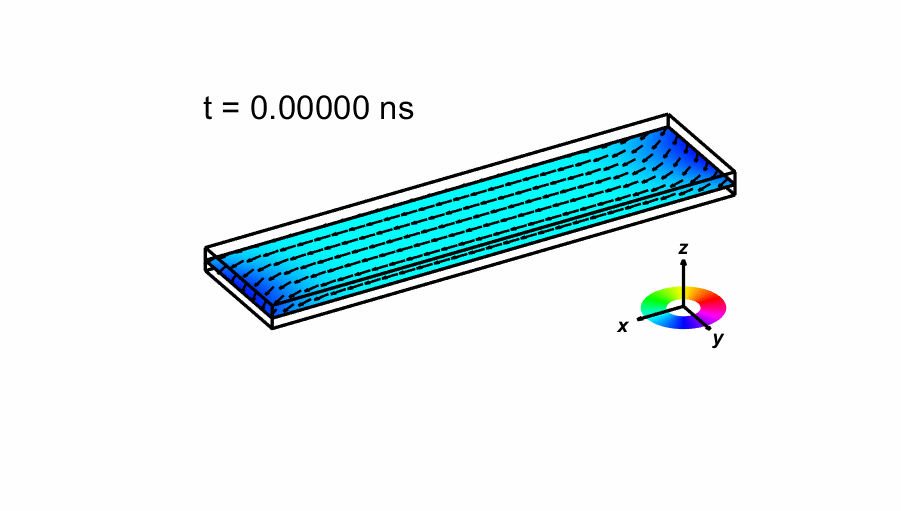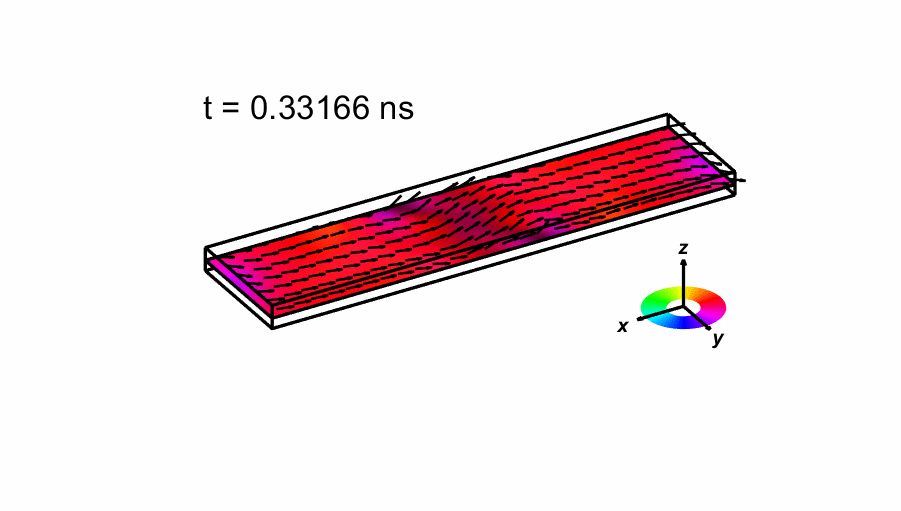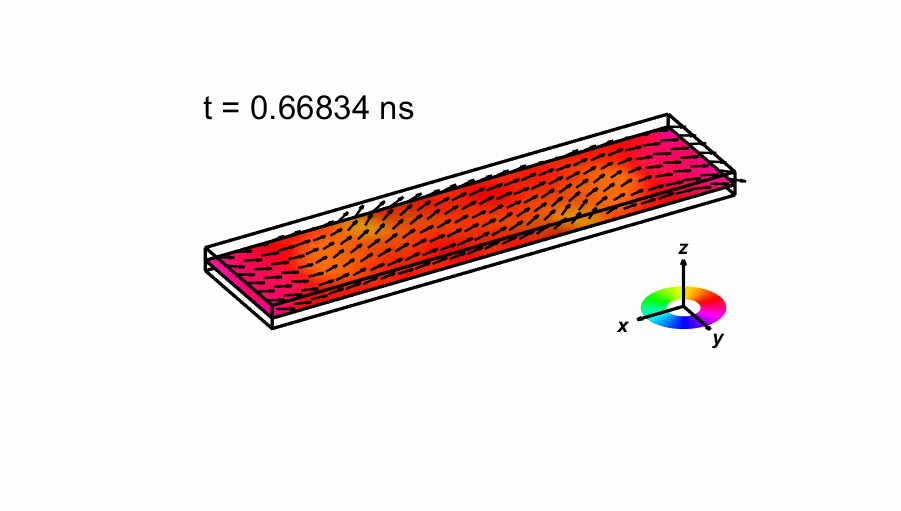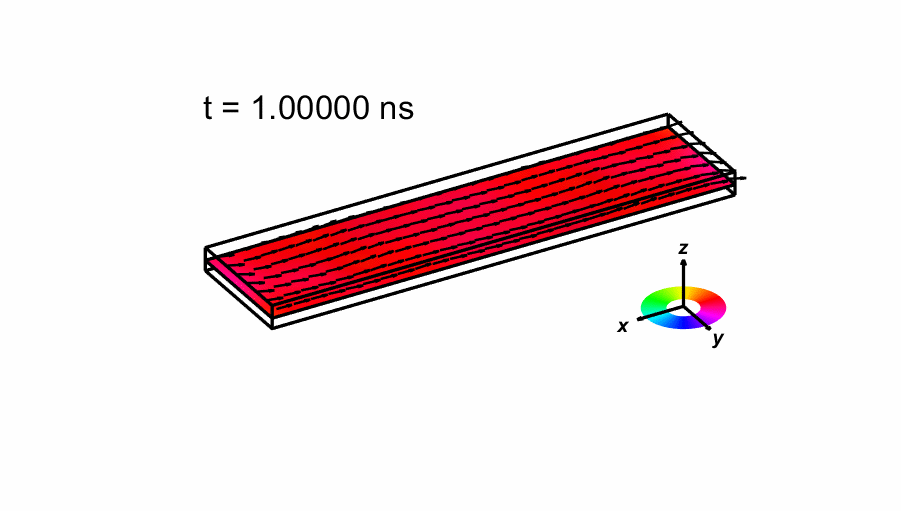
• Field applied: μ₀H= [-35.5,-6.3,0.0] mT. Again the different components of the spatially averaged normalized magnetization as function of time is shown below up to t = 1 ns.
  
  We also shown an image of the magnetization when first crosses zero below, as well as an animated sequence of the time evolution of the magnetization. The number of arrows drawn has been reduced from the actual 160x40 simulation. The color indicate the direction of the magnetization as shown in the small legend.
  
  
  

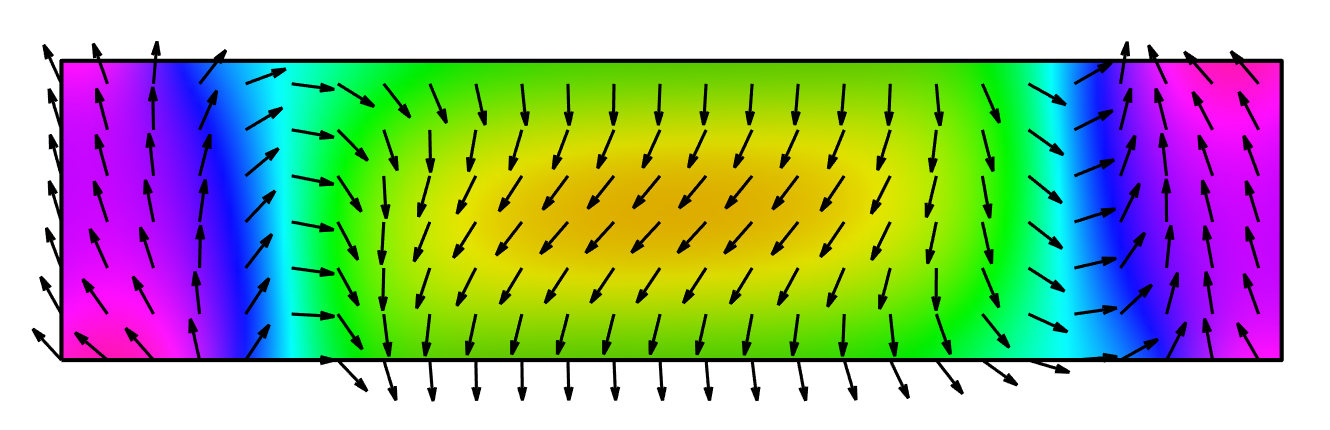
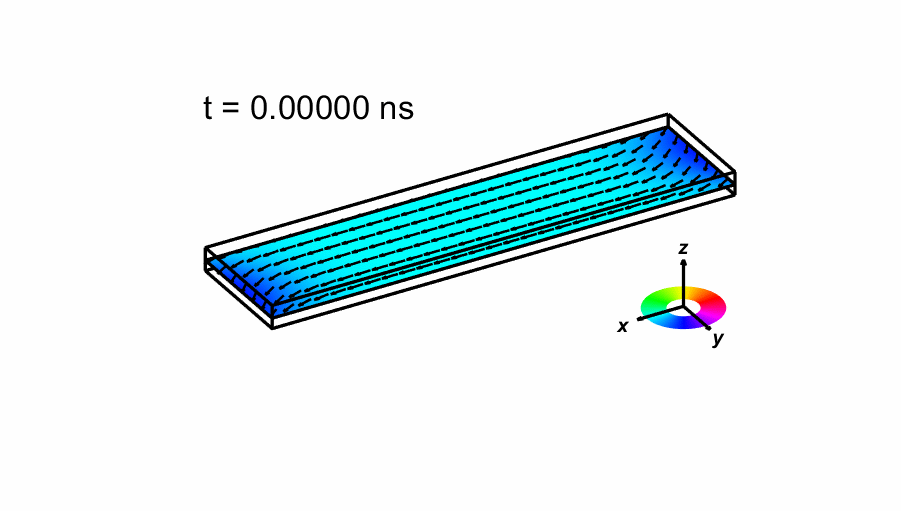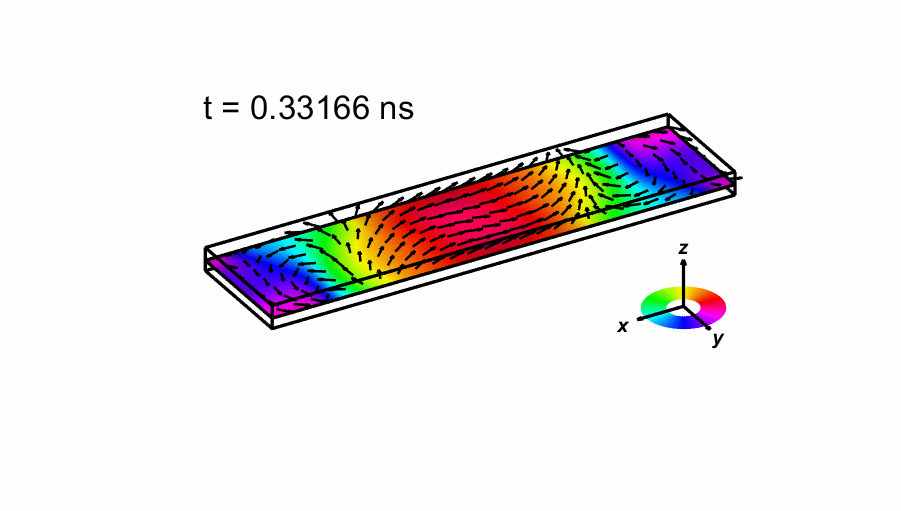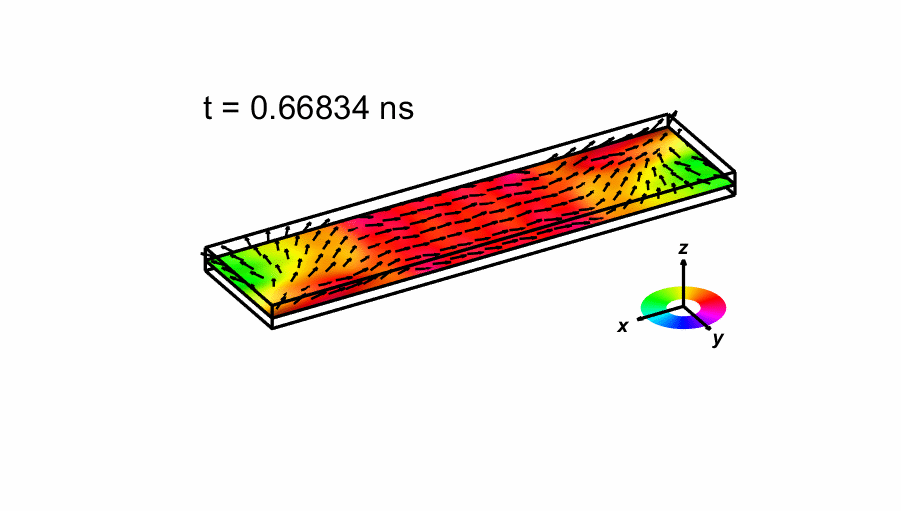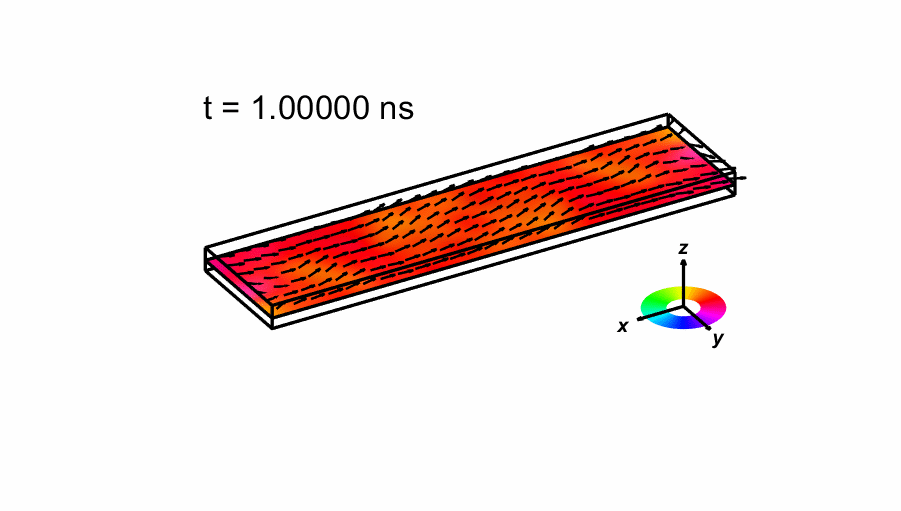
Data:

• Field 1: Time series of magnetization and vector components of the magnetization when < m_x > = 0.
• Field 2: Time series of magnetization and vector components of the magnetization when < m_x > = 0.

References: