µMAG Standard Problem #4 results

Disclaimer

Solution directory

• Comparisons
• G. Albuquerque, J. Miltat and A. Thiaville
• R. D. McMichael, M. J. Donahue, D. G. Porter, and J. Eicke
• Liliana Buda, Lucian Prejbeanu, Ursula Ebels and Kamel Ounadjela
• E. Martinez, L. Torres and L. Lopez-Diaz
• José L. Martins and Tania Rocha
• P.E. Roy and P. Svedlindh
• Massimiliano d’Aquino, Claudio Serpico, and Giovanni Miano
• Dmitri Berkov
• M. J. Donahue and D. G. Porter
• Rasmus Bjørk, E. B. Poulsen and A. R. Insinga

Submitted Solution: Liliana Buda, Lucian Prejbeanu, Ursula Ebels and Kamel Ounadjela

Date:

November 27, 2000

From:

Liliana Buda, Lucian Prejbeanu, Ursula Ebels and Kamel Ounadjela
Institut de Physique et Chimie des Matériaux
Groupe d'Etude des Matériaux Métalliques
23, rue du Loess, 67037 Strasbourg Cedex, France

Contact:

L. D. Buda

A 3D code has been used for these numerical investigations. The ferromagnetic system is discretized in N_x × N_y × N_z identical tetrahedral cells having the size h_x × h_y × h_z. The studies presented here implies a single cell across the thickness.

Inside each cell the magnetization is assumed to be uniform. The stray field is evaluated as the average over the magnetic cell [see A. J. Newell, W. Williams, and D. J. Dunlop, J. Geophys. Res. 98, 9551 (1993) and A. Hubert, R. Schäfer, Magnetic Domains, Springer-Berlin, p. 148 (1998)]. The demagnetization field and energy are computed using the FFT method (FFTW subroutines).

The exchange interaction approximation is the "7-point formula" applied to the 3D case [see Y. Nakatani, N. Uesaka and N. Hayashi, J. Appl. Phys. 28, 2485 (1989)]. On the free surfaces of the magnetic system the magnetization fullfills the Neumann boundary conditions.

For the integration of the LLG equation the implicit Crank-Nicholson backward scheme is used. Our algorithm uses a constant time step of less than 0.1 ps. After each iteration the magnetization is renormalized in order to satisfy the ferromganetic condition.

The convergence criteria imposes that the residual torque (the maximum value of the torque) to be less than 10^-6.

Results:

• After applying the field at 170° from the x-axis (Field 1):

  
  The time evolution of the magnetization components average calculated using 5.0 nm cells.

  
  The magnetization distribution corresponding to the < M_x > = 0.
  

  
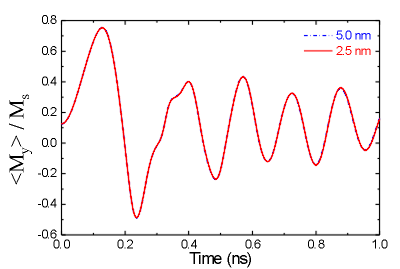
  The effects of the mesh size on the time evolution of the magnetization.
  

• After applying the field at 190° from the x-axis (Field 2):

  
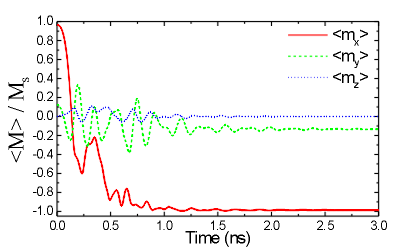
  The time evolution of the magnetization components average calculated using 5.0 nm cells.

  
  The magnetization distribution corresponding to the < M_x > = 0.
  

  
  The effects of the mesh size on the time evolution of the magnetization.

Raw data:

• Field 1: Time series for 2.5 nm mesh, Time series for 5.0 nm mesh, and Vector data at < M_x > = 0.
• Field 2: Time series for 2.5 nm mesh, Time series for 5.0 nm mesh, and Vector data at < M_x > = 0.

References: