µMAG Standard Problem #4 results
See the problem specification.
Disclaimer
µMAG could not succeed without the contributions
of colleagues working outside NIST. Although we value the
contributions made by these colleagues, NIST does not necessarily
endorse the views expressed or the data presented in the submitted
solutions shown below.
Solution directory
-
Comparisons
- G. Albuquerque,
J. Miltat and A. Thiaville
-
R.
D. McMichael, M. J. Donahue, D. G. Porter, and J. Eicke
-
Liliana Buda,
Lucian Prejbeanu, Ursula Ebels and Kamel Ounadjela
-
E. Martinez,
L. Torres and L. Lopez-Diaz
-
Jos�
L. Martins and Tania Rocha
-
P.E. Roy and P. Svedlindh
-
Massimiliano
d’Aquino, Claudio Serpico, and Giovanni Miano
-
Dmitri Berkov
-
M. J. Donahue and D. G. Porter
-
Rasmus Bjørk, E. B. Poulsen and A. R. Insinga
Submitted Solution:
Pierre E. Roy and Peter Svedlindh
- Date:
- November 18, 2005.
- From:
- Pierre E. Roy and Peter Svedlindh
Department of Engineering Sciences,
Ångström Laboratory,
Box 534, SE-751 21 Uppsala University, Uppsala, Sweden
- Contact:
-
Pierre E. Roy
For these calculations, a finite difference scheme has been used with 3D
spins on a 2D mesh (since the thickness of the particle is well below
the exchange length). Exchange interactions were calculated for 4
nearest neighbors using the 5-point approximation for the
Laplacian. Demagnetizing fields have been computed with FFT methods
(W.H. Press, B.P. Flannery, S.A. Teukolsky, William T. Vetterling,
Numerical Recipes, The Art of Scientific Computing, Cambridge
University Press 1988) and the analytical expressions for the evaluation
of the demagnetization tensor used were taken from Newell et
al. (A. J. Newell, W. Williams, and D. J. Dunlop,
J. Geophys. Res. 98, 9551 (1993)). For the integration of
the Landau-Lifshitz equation of motion, a 4th order Runge-Kutta scheme
was implemented. Two discretization cell sizes have been considered: 5nm
and 2.5nm.
Results:
- Field applied at 170° from the x-axis (Field 1):
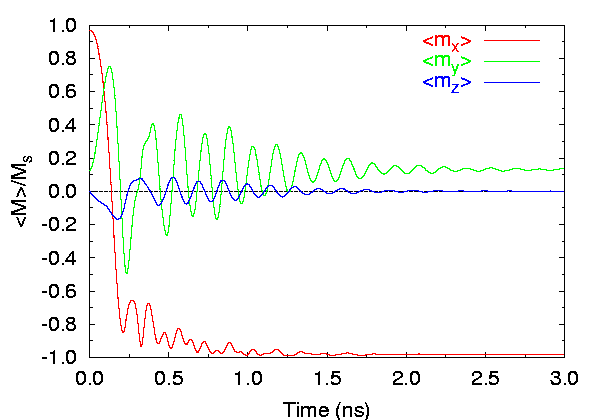
Time evolution of spatially averaged magnetization components, 2.5 nm
cells.
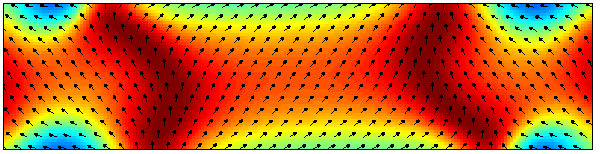
The magnetization distribution corresponding to the first time
< Mx > = 0, with 2.5 nm cells.
Color indicates my-component.
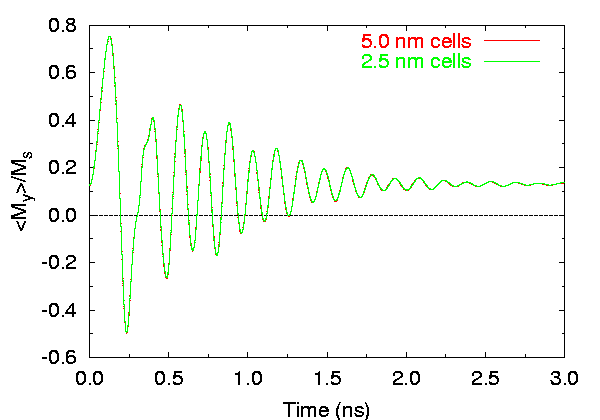
Effects of cell size on time evolution of
< my >.
- Field applied at 190° from the x-axis (Field 2):
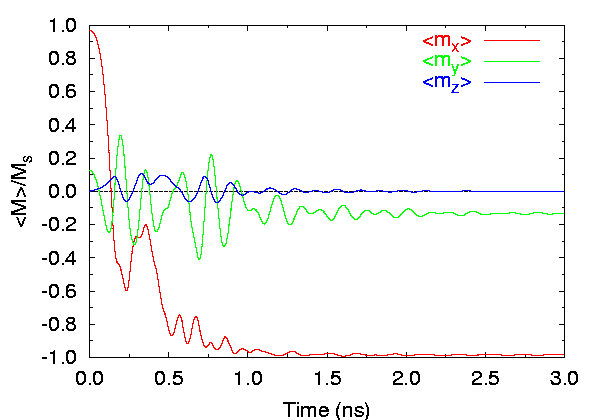
Time evolution of spatially averaged magnetization components, 2.5 nm cells.

The magnetization distribution corresponding to the first time
< Mx > = 0, with 2.5 nm cells.
Color indicates my-component.
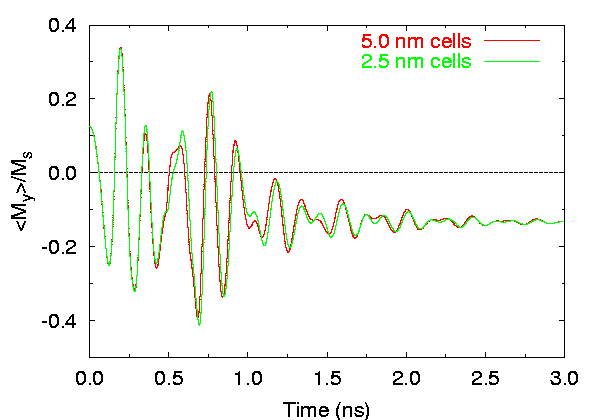
Effects of cell size on time evolution of
< my >.
Data:
Time series data contain 4 columns: time (ns),
mx, my, mz. These files are
gzipped compressed; uncompressed the data files are each roughly 68 MB
for the 2.5 nm mesh data and 16 MB for the 5.0 nm mesh data.
Vector data has 5 columns: x, y position in cells (each
cell is 2.5 nm), and mx, my,
mz normalized vector components.
Please send comments to [email protected] and join the
µMAG discussion e-mail list.
Site Directory
µMAG organization / NIST CTCMS /
[email protected]
11-NOV-2021





