OOF2: The Manual
Name
SS22 (SS22) — Zienkowicz and Taylor's SS22 algorithm for solving equations with second order time derivatives.
Synopsis
SS22(theta1,theta2)
Details
-
Base class:
TimeStepper -
Parameters:
theta1- First moment of the weight function for time averages. Type: A real number in the range [0, 1].
theta2- Second moment of the weight function for time averages. Type: A real number in the range [0, 1].
Description
SS22 is a TimeStepper that implements the SS22
algorithm from Zienkiewicz and Taylor[34]. Like CrankNicolson, it is a second order
method, so its error is of order 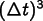 on each step. Unlike CrankNicolson and the other time
steppers in OOF2,
on each step. Unlike CrankNicolson and the other time
steppers in OOF2, SS22 integrates second
order time derivatives directly, without resorting to equation (6.141).
SS22 works by expanding the field values
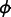 in a
Taylor series in time
in a
Taylor series in time
where 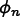 and
and
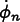 are vectors of
are vectors of
Field values and their time derivatives at time
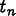 ,
,
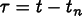 is the time within the time step, and
is the time within the time step, and
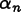 is unknown. This expression is inserted into the differential
equation being solved (e.g, equation
(2.9)) and integrated over the
duration
is unknown. This expression is inserted into the differential
equation being solved (e.g, equation
(2.9)) and integrated over the
duration 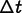 of the time step with a weighting
function
of the time step with a weighting
function 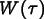 .
. 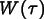 plays the role of a
finite element shape function in the time coordinate. The result is
a matrix equation which can be solved for
plays the role of a
finite element shape function in the time coordinate. The result is
a matrix equation which can be solved for 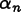 , which in turn gives
the
, which in turn gives
the Field values and time derivatives at the end of the step, via
equation (6.161).
The exact form of the weighting function 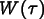 turns out to be
irrelevant. All that is needed are its first and second moments,
which must be provided as the parameters
turns out to be
irrelevant. All that is needed are its first and second moments,
which must be provided as the parameters theta1
and theta2. The k-th moment is defined by
Using small values near 0 will make SS22 act
more like an explicit method, and values near 1 will make it more
like an implicit method. Values near 0.5 seem to work well.
SS22 can be used on first order equations,
such as the heat equation, although it's most advantageous for
second order equations, like the force balance equation.
[34] O.C. Zienkiewicz and R.L. Taylor, The Finite Element Method, Fifth Edition, Volume 1, page 511.


![\[ \phi = \phi_n + \tau\dot\phi_n + \frac12 \tau^2\alpha_n \]](equations/6.5.2-eq-38.gif)
![\[
\theta_k = \frac1{\Delta t^k}
\frac{\int_0^{\Delta t} W(\tau) \tau^k\,d\tau}
{\int_0^{\Delta t} W(\tau)\,d\tau}
\]](equations/6.5.2-eq-39.gif)

