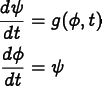OOF2: The Manual

`Forward Euler (ForwardEuler)`
	6.5.2. Subclasses

Name

Forward Euler (ForwardEuler) — Fully explicit first order time stepping.

Synopsis

ForwardEuler()

Details

Base class: TimeStepper

Description

The Forward Euler method is the simplest method of numerically integrating ordinary differential equations. The individual steps are very quick to compute, but the method is often unstable, requiring very small step sizes. It is first order in time, meaning that it makes an error of order 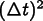$(\Delta t)^2$ on each step.

Given a vector 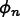$\phi_n$ of unknowns (i.e. Field values in OOF2) at time 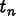$t_n$ , and the first order differential equation

$\frac{d\phi}{dt} = f(\phi, t)$

(6.137)

the Forward Euler estimate for 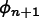$\phi_{n+1}$ is

$\phi_{n+1} = \phi_n + \Delta t f(\phi_n, t_n)$

(6.138)

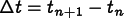where $\Delta t = t_{n+1}-t_n$ .

ForwardEuler can be applied to equations with second order time derivatives

$\frac{d^2\phi}{dt^2} = g(\phi, t)$

(6.139)

by defining new variables

$\psi = \frac{d\phi}{dt}$

(6.140)

and solving the augmented set of first order equations

$\begin{align*} \frac{d\psi}{dt} &= g(\phi, t) \\ \frac{d\phi}{dt} &= \psi \end{align*}$

(6.141)

ForwardEuler works equally well for linear and nonlinear equations. Because the method is explicit, equation (6.138) doesn't require a nonlinear solver even if 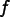$f$ is nonlinear.


`Forward (ForwardAnimation)`		`All Segments (FromAllSegments)`