OOF2: The Manual
Name
Crank-Nicolson (CrankNicolson) — Semi-implicit first order time stepping, theta=0.5.
Synopsis
CrankNicolson()
Description
The Crank-Nicolson method is a method of
numerically integrating ordinary differential equations. It is
second order in time, meaning that it makes an error only of order
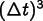 on each step, and is more accurate and more
stable than the ForwardEuler
method, but it is more expensive to compute.
on each step, and is more accurate and more
stable than the ForwardEuler
method, but it is more expensive to compute.
Given a vector 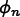 of unknowns
(i.e.
of unknowns
(i.e. Field values in OOF2) at
time 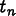 ,
and the first order differential equation
,
and the first order differential equation
the Crank-Nicolson estimate for 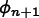 is
is
where 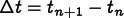 . The need to solve equation (6.129) for
. The need to solve equation (6.129) for 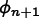 , which appears on
both sides, makes
, which appears on
both sides, makes CrankNicolson a
semi-implicit method, requiring more CPU time than
an explicit method such as ForwardEuler, especially when
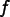 is
nonlinear.
is
nonlinear.
CrankNicolson can be applied to equations
with second order time derivatives via equation (6.141).
Generalized Euler Methods
CrankNicolson is an example of a
Generalized Euler method, which is a
combination of the ForwardEuler
and BackwardEuler methods:
where 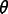 is a number between 0
and 1.
is a number between 0
and 1. 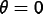 gives the fully
explicit ForwardEuler
method.
gives the fully
explicit ForwardEuler
method. 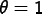 gives the fully
implicit BackwardEuler method.
Intermediate values give semi-implicit methods, such as CrankNicolson (
gives the fully
implicit BackwardEuler method.
Intermediate values give semi-implicit methods, such as CrankNicolson (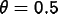 ).
).
The error in the generalized Euler methods is of order
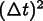 , except for CrankNicolson, which is
, except for CrankNicolson, which is
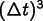 .
.


![\[ \frac{d\phi}{dt} = f(\phi, t) \]](equations/6.5.2-eq-5.gif)
![\[ \phi_{n+1} = \phi_n +
\frac12 \Delta t \left[f(\phi_n, t_n) + f(\phi_{n+1},t_{n+1})\right]
\]](equations/6.5.2-eq-6.gif)
![\[ \phi_{n+1} = \phi_n +
\Delta t \left[ (1-\theta)f(\phi_n,t_n) + \theta f(\phi_{n+1},t_{n+1})
\right]
\]](equations/6.5.2-eq-7.gif)

