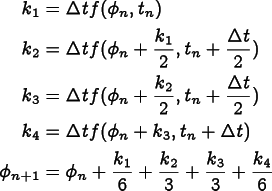OOF2: The Manual

`4th order Runge-Kutta (RK4)`
	6.5.2. Subclasses

Name

4th order Runge-Kutta (RK4) — Fourth order Runge-Kutta time stepping.

Synopsis

RK4()

Details

Base class: TimeStepper

Description

RK4 is a TimeStepper that implements the classic fourth order Runge-Kutta method for solving ordinary differential equations. The error on each step is of order 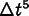$\Delta t^5$ .

Given a vector 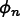$\phi_n$ of unknowns (i.e. Field values in OOF2) at time 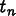$t_n$ , and the first order differential equation

$\frac{d\phi}{dt} = f(\phi, t)$

(6.157)

the fourth order Runge-Kutta estimate for 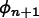$\phi_{n+1}$ is given by

$\begin{align*} k_1 &= \Delta t f(\phi_n, t_n) \\ k_2 &= \Delta t f(\phi_n+\frac{k_1}{2}, t_n+\frac{\Delta t}{2}) \\ k_3 &= \Delta t f(\phi_n+\frac{k_2}{2}, t_n+\frac{\Delta t}{2}) \\ k_4 &= \Delta t f(\phi_n+k_3, t_n+\Delta t) \\ \phi_{n+1} &= \phi_n + \frac{k_1}{6} + \frac{k_2}{3} + \frac{k_3}{3} + \frac{k_4}{6} \end{align*}$

(6.158)

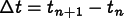where $\Delta t = t_{n+1}-t_n$ .

RK4 can be applied to second order equations by using equation (6.141).

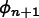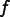Because the method is explicit ( $\phi_{n+1}$ doesn't appear as an argument to $f$ ), equation (6.158) doesn't require a nonlinear solver even if 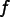$f$ is nonlinear.


`2nd order Runge-Kutta (RK2)`		`Range (RangeOutput)`