OOF: Finite Element Analysis of Microstructures
Next: trigonalA Up: Element Types and their Previous: orthorhombic Contents
Subsections
eds_el
This element is named after Ed Fuller, who suggested it4.2. It is an element which is
isotropic in its elastic coefficients, but is orthorhombic in its
thermal expansion coefficients. It can be used to simulate
transformation strains or residual stresses where the elastic
coefficients are not known precisely, but the expansions are known not
to be isotropic.
Parameters
- elastic coefficients
- The elastic coefficients young and poisson have the same
meaning as they do in the isotropic element (Section
4.5.1. [stress]
- thermal expansion coefficients
- The thermal expansion coefficients a1, a2, and a3 are the
diagonal components of the thermal expansion tensor
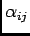 .
4.3 [inverse temperature]
.
4.3 [inverse temperature]
- orientation
- Without rotation, the thermal expansion coefficient a1 governs
expansion in the
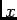 direction, a2 in the
direction, a2 in the 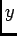 direction, and
a3 in the
direction, and
a3 in the 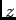 direction (out of the screen). See Section
4.3. [degrees]
direction (out of the screen). See Section
4.3. [degrees]
 |
Next: trigonalA Up: Element Types and their Previous: orthorhombic Contents /* Send mail to the OOF Team *//* Go to the OOF Home Page */