OOF: Finite Element Analysis of Microstructures

Rotations next up previous contents
Next: Physical Units Up: The Element Types Previous: Plane Stress and Plane   Contents


Rotations

The orientation variable in figure 4.1 illustrates how the orientation of the material in an element is specified. In the general case, three angles are required to specify an orientation. We use the Euler angles to describe one rotation as the result of three simpler rotations. Historically, Euler angles have been the source of much confusion, so, as our contribution to history, we present multiple ways of thinking about them. Different authors use different conventions, so don't assume that our definition is the same as yours!

A rotation is entered as three values, in degrees, with square brackets: [ $\alpha$, $\beta$, $\gamma$ ]. If only one number is specified (without brackets), it is taken as the $\beta$ value. That is, 30 is equivalent to [0, 30, 0] and is the same as rotating about an axis normal to the OOF screen. Note that [0, 0, X] is also equivalent to [0, X, 0].

We define $(\hat {\bf x}, \hat {\bf y}, \hat {\bf z})$ to be the screen coordinate system, with $\hat {\bf x}$ pointing to the right, $\hat {\bf y}$ upwards, and $\hat {\bf z}$ out of the screen. We will call the crystal axes $(\hat {\bf a}, \hat {\bf b}, \hat {\bf c})$. As usual, all rotations are right handed, ie. a positive rotation about an axis is counterclockwise if the axis is pointing towards you.

One way of finding the Euler angles: This method describes the rotation that must be applied to the crystal axes to bring them into alignment with the screen axes, assuming that the crystal starts in its desired orientation with respect to the screen. First, rotate the axes by $\beta$ around the $\hat{\bf c}$ axis. This defines new axes $(\hat{\bf a}', \hat{\bf b}', \hat{\bf c})$. Next rotate by $\alpha$ about the $\hat{\bf b}'$ axis, defining another coordinate system $(\hat{\bf a}'', \hat{\bf b}', \hat{\bf c}'')$. Finally rotate by $\gamma$ about the $\hat{\bf c}''$ axis, bringing the axes into agreement with $(\hat {\bf x}, \hat {\bf y}, \hat {\bf z})$.

An equivalent way: Consider the material oriented with a globe, with the origin at the center of the earth and $\hat{\bf c}$-axis pointing towards the north pole, the $\hat{\bf a}$-axis pointing at the Greenwich Meridian where it intersects the equator and the $\hat{\bf b}$-axis pointing towards the Indian ocean somewhere southeast of Sri Lanka. The unrotated globe has its $\hat{\bf a}$, $\hat{\bf b}$, and $\hat{\bf c}$ axes aligned with the $\hat {\bf x}$, $\hat {\bf y}$, and $\hat {\bf z}$ axes of the screen, respectively. The rotation triplet describes how to rotate the material into its desired orientation. The first number of the rotation triplet tilts the point on the north pole southward along the Greenwich Meridian by $-\alpha$ degrees to a new latitude. The second number spins the globe to the east by $-\beta$ degrees about its (tilted) $\hat{\bf c}$-axis. The third number rotates the tilted globe to the east by $-\gamma$ degrees about the screen's $\hat {\bf z}$ axis.

Yet another way: The order of rotations in the previous definition can be rearranged. Rotate the globe to the east by $-\beta$ degrees about the $\hat {\bf z}$-axis, tilt the north pole by $-\alpha$ about the $\hat {\bf y}$-axis, and rotate to the east by $-\gamma$ again about the $\hat {\bf z}$-axis.

A prescription: If you know the components in the crystal coordinate system of the screen vectors $\hat {\bf x}$, $\hat {\bf y}$, and $\hat {\bf z}$, you can compute the Euler angles as follows. Let $(x_1, x_2, x_3)$ be the components of the screen's $\hat {\bf x}$-axis in the crystal coordinate system. Let $(y_1, y_2, y_3)$ and $(z_1, z_2, z_3)$ similarly be the components of the $\hat {\bf y}$ and $\hat {\bf z}$-axes. Then

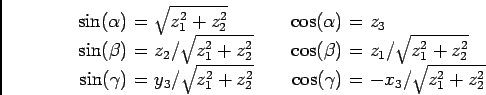
\begin{displaymath} \begin{array}{r@{ }c@{ }l@{ }r@{ }c@{ }l} \si... ...\gamma) &=& -x_3/\sqrt{z_1^2 + z_2^2} \\ \end{array}\nonumber \end{displaymath}

next up previous contents
Next: Physical Units Up: The Element Types Previous: Plane Stress and Plane   Contents
/* Send mail to the OOF Team *//* Go to the OOF Home Page */