These calculations were done using a finite-difference scheme, always with two cells across the thickness of the sample. Three mesh sizes were used: approx. 1 nm cells, approx. 2 nm cells and approx. 4 nm cells (in the two larger axis of the sample).
The LLG equations were solved using 2nd order or 4th order Runge-Kutta. time step of 1e-14 s and adaptive time step (if torque surpasses a specific value, time step is decreased to half its value, if torque is considered very low, time step is doubled to speed up calculations).
The demagnetization field is calculated solving the Poisson equation numerically using a Multigrid method. The boundary conditions are obtained calculating multipole expansion of magnetic charge inside bigger cells and then integrating this expansion.
Exchange interactions were calculated for the 6 neighbours (well, in this case, 5 neighbours) of each cell.
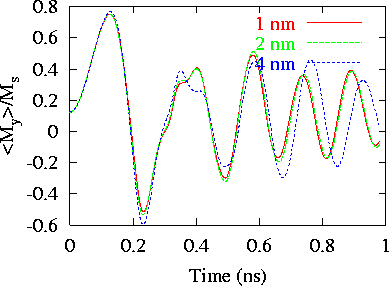
Results obtained for Field 1 with 1 nm cells and 2 nm cells are very similar, almost equal. Results obtained with 4 nm cells have some differences.
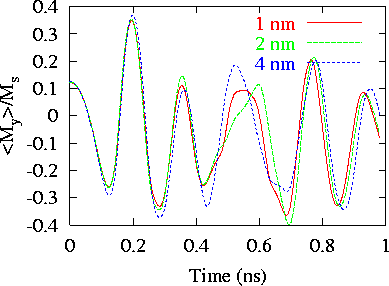
Results for Field 2 are different for different mesh sizes, and these differences increase as time passes.
