µMAG Standard Problem #4 results
See the problem specification.
Disclaimer
µMAG could not succeed without the contributions
of colleagues working outside NIST. Although we value the
contributions made by these colleagues, NIST does not necessarily
endorse the views expressed or the data presented in the submitted
solutions shown below.
Solution directory
-
Comparisons
- G. Albuquerque,
J. Miltat and A. Thiaville
-
R.
D. McMichael, M. J. Donahue, D. G. Porter, and J. Eicke
-
Liliana Buda,
Lucian Prejbeanu, Ursula Ebels and Kamel Ounadjela
-
E. Martinez,
L. Torres and L. Lopez-Diaz
-
Jos�
L. Martins and Tania Rocha
-
P.E. Roy and P. Svedlindh
-
Massimiliano
d’Aquino, Claudio Serpico, and Giovanni Miano
-
Dmitri Berkov
-
M. J. Donahue and D. G. Porter
-
Rasmus Bjørk, E. B. Poulsen and A. R. Insinga
Submitted Solution: Massimiliano d’Aquino, Claudio Serpico, and Giovanni Miano
- Date:
- November 20, 2005.
- From:
- Massimiliano d’Aquino, Claudio Serpico,
and Giovanni Miano
Dipartimento di Ingegneria Elettrica, Università degli
Studi di Napoli “Federico II”, I-80125 Napoli – Italy
- Contact:
-
Massimiliano d’Aquino
A 3D micromagnetic code has been used for these calculations. The
Landau-Lifshitz-Gilbert (LLG) equation has been solved with a
semi-discretized approach.
The spatial discretization has been performed with the finite
difference method. The magnetic body has been subdivided into a
collection of N rectangular prisms with edges parallel to the
coordinate axes (N = Nx × Ny ×
Nz, where Nx, Ny,
Nz are the number of cells along the axes x, y,
z respectively). The magnetization has been assumed uniform within
each cell.
The exchange field has been computed by means of a 7-point laplacian
discretization, which is second order accurate in space. The Neumann
boundary condition has been taken into account on the boundary
cells. The magnetostatic field has been written as a discrete
convolution whose kernel was obtained by means of generalization to
prism (non cubic) cells of the formulas proposed in Ref. [1] for cubic
cells. Such discrete convolution has been computed by using 3D Fast
Fourier Transform with zero-padding algorithm.
The time integration of the (spatially) semi-discretized LLG equation
has been performed by using the (implicit) mid-point rule numerical
technique. This technique is unconditionally stable and second order
accurate with respect to the time step. In addition, when the mid-point
rule scheme is applied to the LLG equation, it preserves the fundamental
properties of the LLG dynamics, regardless of the time-step:
- Magnetization magnitude conservation at each spatial location.
- LLG Lyapunov structure (for constant in time external field),
namely the magnetic free energy is a decreasing function of time.
Moreover, in the case of zero damping α=0, the free energy is
exactly preserved regardless of the time step and the hamiltonian
structure of the LLG equation is preserved up to third-order with
respect to the time step. Details about the application of the mid-point
rule to micromagnetic simulations can be found in Ref. [2].
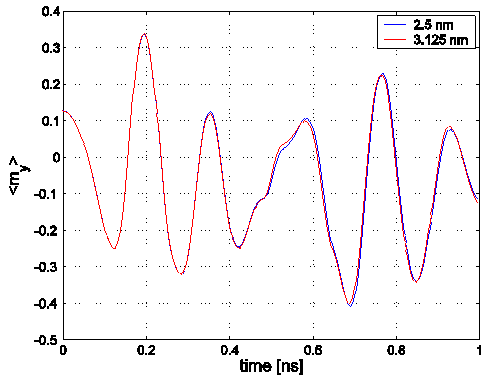
In all the computations, the time-step was constant and set to 2.5
ps. The magnetization has been assumed to have reached an equilibrium
state when the maximum value of the normalized torque was less than
10-5.
Results:
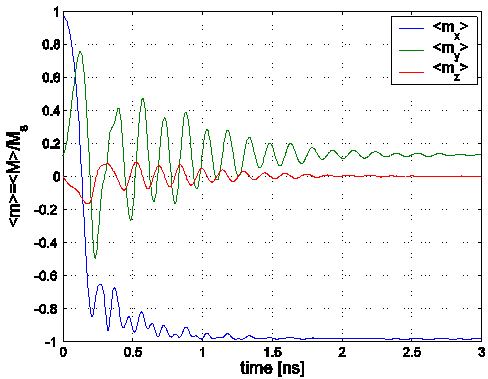
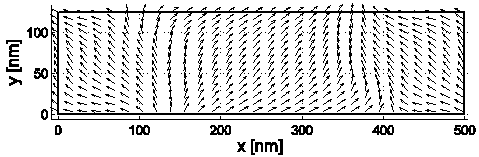
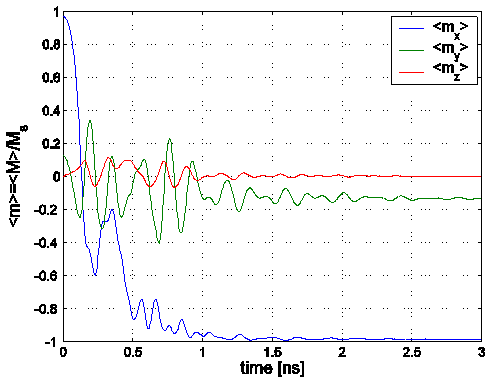
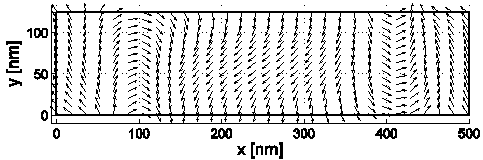
Data:
Time series data contain 4 columns: time (ns),
mx, my, mz. Vector data has
6 columns: x, y, z coordinates (in meters), and
mx, my, mz vector
components.
References:
[1] M.E. Schabes and A. Aharoni, Magnetostatic Interaction Fields for
a Three-Dimensional Array of Ferromagnetic Cubes, IEEE Transactions on
Magnetics 23, n. 6 (1987), 3882-3888.
[2] M. d’Aquino, C. Serpico, G. Miano, Geometrical integration
of Landau-Lifshitz-Gilbert equation based on the mid-point rule,
Journal of Computational Physics 209 (2005), 730-753.
Please send comments to [email protected] and join the
µMAG discussion e-mail list.
Site Directory
µMAG organization / NIST CTCMS /
[email protected]
11-NOV-2021