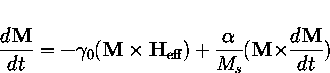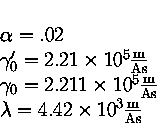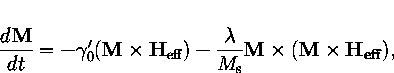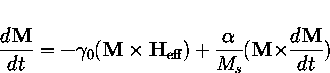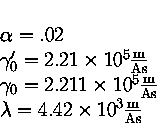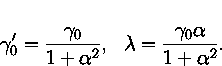µMAG Standard Problem #4
Problem brainstormed by Bob McMichael, Roger Koch and Thomas Schrefl;
developed by Jason Eicke and Bob McMichael.
Please send comments to [email protected]
and join the µMAG discussion e-mail
list for ongoing discussion.
Sets of solutions are available.
Specifications
Standard problem #4 is focused on dynamic aspects of micromagnetic computations.
The initial state is an equilibrium s-state
such as is obtained after applying and slowly reducing a saturating field
along the [1,1,1] direction to zero. Fields of magnitude sufficient
to reverse the magnetization of the rectangle are applied to this
initial state and the time evolution of the magnetization as the system
moves towards equilibrium in the new fields are examined. The problem
will be run for two different applied fields.
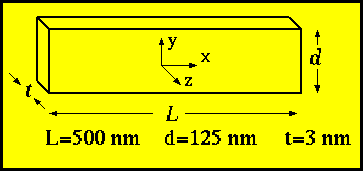
Geometry:
A film of thickness, t=3 nm, length, L=500 nm and width,
d=125
nm will be used.
Material parameters:
Similar to Permalloy:
A = 1.3e-11 J/m (1.3e-6
erg/cm)
Ms = 8.0e5 A/m
(800 emu/cc)
K = 0.0
The dynamics, calculated either using the Landau-Lifshitz equation,
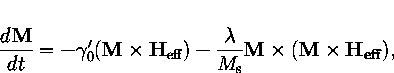
or the Gilbert equation,
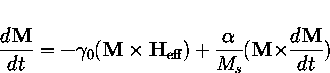
will use parameters,
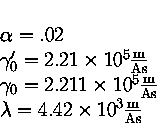
Note that these parameters are related by the equations:
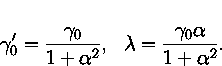
Applied Fields:
Two switching events will be calculated using fields applied in the
x-y
plane of different magnitude and direction.
-
Field 1: µ0Hx=-24.6 mT,
µ0Hy= 4.3 mT, µ0Hz=
0.0 mT which is a field approximately 25 mT, directed 170 degrees
counterclockwise from the positive x axis
-
Field 2: µ0Hx=-35.5 mT,
µ0Hy=-6.3 mT, µ0Hz=
0.0 mT which is a field approximately 36 mT, directed 190 degrees counterclockwise
from the positive x axis
Each field will be applied instantaneously at t=0 to the equilibrium
s-state
.
Comparison:
Two outputs are desired for comparison:
-
The (x,y,z) components of the spatially averaged magnetization of
the sample as a function of time from t=0 until the sample reaches
equilibrium in the new field
-
An image of the magnetization at the time when the x-component
of the spatially averaged magnetization first crosses zero
The magnetization values in the time series data should be normalized
by Ms.
The time series data is desired so that a detailed
comparison can be made between
solutions. The magnetization images are to check for any differences
in the reversal mechanisms if the time data between solutions
is different.
Please see the µMAG standard problem strategy
page for information on publicizing your results.
Comments:
The problem was chosen so that resolving the dynamics should easier for
the 170 degree applied field than the 190 degree applied field.
Preliminary simulations reveal that, in the case of the field applied at
170 degrees, the magnetization in the center of the rectangle rotates in
the same direction as at the ends during reversal. In the 190 degree
case, however, the center rotates the opposite direction as the ends resulting
in a more complicated reversal. The field amplitudes were chosen
to be about 1.5 times the coercivity in each case.
The results should be shown to be independent of the discretization
size.
Site Directory
µMAG organization / NIST CTCMS /
[email protected]
29-FEB-2000 by Jason Eicke