



Next: Boundary elements
Up: Theory
Previous: Basics
Now, let's consider the ``fundamental solution'' u*i, which is the solution to
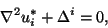 |
(6.4) |
where 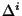 is the Dirac delta function at point i, i.e.
is the Dirac delta function at point i, i.e.
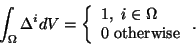 |
(6.5) |
We know that
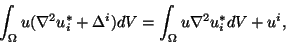 |
(6.6) |
so since u*i satisfies equation 6.4, equation 6.3 becomes
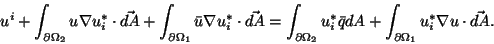 |
(6.7) |
Incidentally, this allows the calculation of u at any internal point igiven the u and
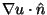 values on the boundary, according to
values on the boundary, according to
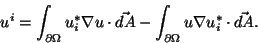 |
(6.8) |
The ``fundamental solutions'' u*i that fit in here are
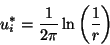 |
(6.9) |
in 2-D (r is the distance from point i), and
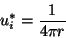 |
(6.10) |
in 3-D. For a point i on the surface, because the singularity intersects the
integration path, we modify equation 6.7 to read:
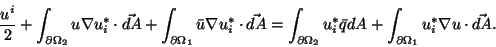 |
(6.11) |
(Note: if the surface isn't smooth at point i, ui shouldn't be multiplied
by
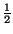 but by something else.) This is valid for both 2-D and 3-D
cases.
but by something else.) This is valid for both 2-D and 3-D
cases.




Next: Boundary elements
Up: Theory
Previous: Basics
Adam Clayton Powell IV
1999-07-23