



Next: Linear elements
Up: Theory
Previous: Fundamental Solution
Beginning with constant elements, if one assumes that u and
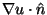 are constant over each element j of which the surface is
comprised, then equation 6.11 becomes
are constant over each element j of which the surface is
comprised, then equation 6.11 becomes
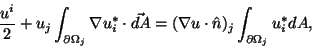 |
(6.12) |
where summation is implied for like indices (Einstein notation). Defining the
matrices
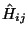 and Gij according to the left- and right-side
integrals gives the matrix equation
and Gij according to the left- and right-side
integrals gives the matrix equation
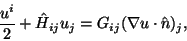 |
(6.13) |
which can be simplified further by defining
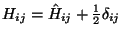 to give
to give
 |
(6.14) |
Rearranging the matrix columns and vector rows so that unknowns go on the left
and knowns on the right (i.e. for nodes j in
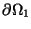 ,
uj goes
on the right and
,
uj goes
on the right and
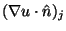 on the left; vice versa for
on the left; vice versa for
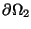 )
gives the matrix equation which solves the problem.
)
gives the matrix equation which solves the problem.
Note that for constant and linear elements,
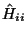 is zero because
is zero because
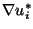 is orthogonal to the surface normal. Also, Gii for
constant elements can be calculated analytically, and in 2-D is equal to
is orthogonal to the surface normal. Also, Gii for
constant elements can be calculated analytically, and in 2-D is equal to
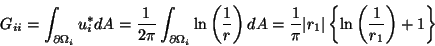 |
(6.15) |
where |r1| is half the element width.




Next: Linear elements
Up: Theory
Previous: Fundamental Solution
Adam Clayton Powell IV
1999-07-23
![]() is zero because
is zero because
![]() is orthogonal to the surface normal. Also, Gii for
constant elements can be calculated analytically, and in 2-D is equal to
is orthogonal to the surface normal. Also, Gii for
constant elements can be calculated analytically, and in 2-D is equal to