OOF2: The Manual
Name
GMRES (GeneralizedMinResidual) — Generalized Minimal Residual method for iteratively solving non-symmetric matrices.
Synopsis
GeneralizedMinResidual(preconditioner,tolerance,max_iterations,krylov_dimension)
Details
-
Base class:
MatrixMethod -
Parameters:
preconditioner- Black magic for making the matrix more easily solvable. Type: An object of the
Preconditionerclass. tolerance- Largest acceptable relative error in the matrix solution. Type: A real number.
max_iterations- Maximum number of iterations to perform. Type: Integer.
krylov_dimension- Making the Krylov dimension bigger will improve convergence but use more memory. Type: Integer.
Description
The GMRES matrix method implements the
preconditioned Generalized Minimal Residual method for
solving
linear matrix equations in AdvancedSolverMode. The matrix does not
have to be symmetric.
GMRES is an iterative method, meaning that it
creates an approximate solution and improves it on each iteration.
The iteration will cease when the relative error of the solution is
less than the given tolerance. The solver will
stop and report an error if the tolerance isn't satisfied within
max_iterations iterations.
GMRES (and other Krylov space methods) work by searching for
a solution in a subspace of the full vector space.[29]
The dimension of this subspace is given by the
krylov_dimension parameter. Using a larger
krylov_dimension will improve the convergence of
the method, but will require more memory.
The preconditioner parameter specifies which
Preconditioner to use, if any.
Preconditioners
speed the convergence of iterative methods by replacing the
original matrix by something closer to the identity matrix.
[29]
If 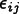 is an
initial guess for the solution of
is an
initial guess for the solution of
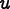 ,
then the initial residual is
,
then the initial residual is
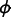 .
The Krylov space of dimension
.
The Krylov space of dimension
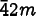 is spanned by the
vectors
is spanned by the
vectors
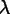 .
GMRES finds the best solution in this space, and then restarts
with a new
.
GMRES finds the best solution in this space, and then restarts
with a new
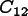 .
If
.
If
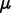 is large
enough, fewer restarts are required, but more data must be retained.
is large
enough, fewer restarts are required, but more data must be retained.