OOF2: The Manual
Name
Z-Z Estimator (ZZ_Estimator) — Error estimation by Zienkiewicz and Zhu's superconvergent patch recovery.
Synopsis
ZZ_Estimator(norm,flux,threshold)
Description
ZZ_Estimator is an ErrorEstimator used when modifying a
Mesh by adaptive mesh
refinement. It uses the Superconvergent Patch Recovery
technique of Zienkiewicz and Zhu.[37]
The error of the finite element approximation
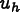 with respect to the
exact solution
with respect to the
exact solution
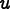 is
is
and the error of the flux (proportional to gradients of
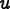 ) is
) is
These definitions are nearly useless, however, because the exact
solutions
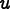 and
and
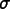 are almost always unknown. It is therefore necessary to invent a
way of estimating the error.
are almost always unknown. It is therefore necessary to invent a
way of estimating the error.
The error estimate procedure developed by Zienkiewicz and Zhu, employing Superconvergent Patch Recovery has proved to be effective and economical both in evaluating errors and driving adaptive mesh refinement.
It is well known that the field derivatives and fluxes
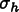 computed from the finite element solutions
computed from the finite element solutions
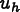 do not possess interelement continuity and have a low accuracy at
nodes and element boundaries. However, there are points within
elements, known as superconvergent points, at
which the derivatives and fluxes are more accurate than at any
other point within the element: values at the superconvergent
points converge more quickly to the true values as the element
size decreases. It is possible to get (or
recover) a more accurate value
do not possess interelement continuity and have a low accuracy at
nodes and element boundaries. However, there are points within
elements, known as superconvergent points, at
which the derivatives and fluxes are more accurate than at any
other point within the element: values at the superconvergent
points converge more quickly to the true values as the element
size decreases. It is possible to get (or
recover) a more accurate value
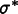 of the stress
of the stress
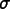 at a node by interpolating between the stresses at the
superconvergent points in a small set of elements (a
patch) around the node.
at a node by interpolating between the stresses at the
superconvergent points in a small set of elements (a
patch) around the node.
The ZZ_Estimator compares the recovered and
directly computed values of the given flux and
refines those in which the norm of the relative
error
 is greater than the given
is greater than the given threshold (given as a
percentage).
The remainder of this page is not required reading.
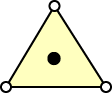
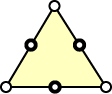
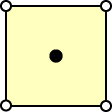
The superconvergent points for various element types are summarized in Table 6.7, where the black dots represent superconvergent points.
Table 6.7. Superconvergent Points of Various Elements Types
| Element Type | Linear | Quadratic |
|---|---|---|
| Triangle |
 |
 |
| Quadrilateral |
 |
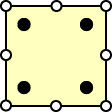 |
Figure 6.117 and Figure 6.118 illustrate typical patches. Only the values of nodes that are completely inside the patch are recovered, unless the patch contains boundaries, in which case values at the edge of the patch are recovered too.
Figure 6.117. Normal Patch Recovery
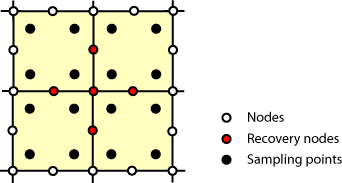
A Typical patch for the Superconvergent Patch Recovery procedure.
Figure 6.118. Boundary Patch Recovery
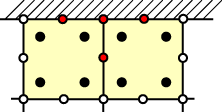
A Boundary patch for the Superconvergent Patch Recovery procedure.
[37]
-
O.C. Zienkiewicz and J.Z. Zhu, The Superconvergent patch recovery and a posteriori error estimators. Part 1. The recovery technique, Int. J. Numer. Methods Eng., 33, 1331-1364 (1992)
-
O.C. Zienkiewicz and J.Z. Zhu, The Superconvergent patch recovery and a posteriori error estimators. Part 2. Error estimates and adaptivity, Int. J. Numer. Methods Eng., 33, 1365-1382 (1992)


![\[e = u - u_h\]](equations/6.5.2-eq-42.gif)
![\[e_\sigma = \sigma - \sigma_h\]](equations/6.5.2-eq-43.gif)

