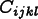OOF2: The Manual
Name
IsotropicRank4Tensor — Representations of an isotropic 4th rank tensor.
Subclasses
Subclasses are listed as they appear in the GUI and (in parentheses) as they appear in scripts.
-
Cij (
IsotropicRank4TensorCij) -- Explicit representation in terms of tensor components. -
Lame (
IsotropicRank4TensorLame) -- Isotropic rank 4 tensor in terms of Lame coefficients. -
E and nu (
IsotropicRank4TensorEnu) -- Isotropic rank 4 tensor in terms of Young's modulus and Poisson's ratio. -
Bulk and Shear (
IsotropicRank4TensorBulkShear) -- Isotropic rank 4 tensor in terms of bulk and shear moduli.
Description
The IsotropicRank4Tensor represents rank 4
tensor properties which are rotationally invariant, such as
isotropic elasticity. The isotropic rank 4 tensor has two
independent components, as shown in Figure 6.56. Because the elasticity
literature uses many different representations of these two
components, OOF2 allows you to enter the tensor in a variety of
formats.
![[Note]](IMAGES/note.png) |
Note |
|---|---|
|
The word “rank” has different meanings in different
fields. Here it means the number of indices on a
tensor.
|
Figure 6.56. Structure of an Isotropic Fourth Rank Tensor
Structure of an isotropic rank 4 tensor. For an explanation of the symbols, see Figure 6.57.
Figure 6.57. Key to the Tensor Diagrams

Symbols used in the tensor diagrams. The symmetries of
symmetric fourth rank tensors,
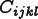 , allow them
to be displayed as second rank tensors,
, allow them
to be displayed as second rank tensors,
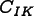 , where
, where
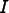 is the Voigt notation for
is the Voigt notation for
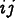 and
and
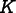 is the Voigt
notation for
is the Voigt
notation for
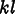 .
To keep things simple(?), the diagrams use Voigt notation
for the columns and
.
To keep things simple(?), the diagrams use Voigt notation
for the columns and
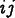 notation for the rows.
notation for the rows.