OOF2: The Manual
| HexagonalRank4TensorCij | ||
|---|---|---|
|
6.7.3. Rank 4 Tensors |  |
Name
HexagonalRank4TensorCij — A rank 4 tensor with hexagonal symmetry
Synopsis
HexagonalRank4TensorCij(c11,
c12, c13,
c33, c44)
Description
A HexagonalRank4TensorCij is a fourth
rank tensor with hexagonal rotational symmetry, expressed in
Voigt notation. The arguments c11,
c12, etc, are
real numbers.
Figure 6.148. Structure of a Hexagonal Fourth Rank Tensor
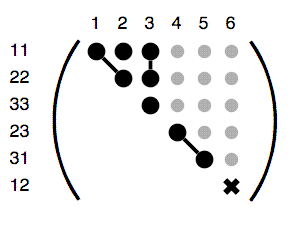
Structure of a hexagonal rank 4 tensor. For an explanation of the symbols, see Figure 6.57.
|
|
 |
|
| TdRank3Tensor |  |
TetragonalRank4TensorCij |