OOF2: The Manual
| MasterCoord | ||
|---|---|---|
|
8.6.7. Coordinate Classes |  |
Name
MasterCoord — Position in master coordinate space
Synopses
C++ Synopsis
#include "engine/mastercoord.h"
class MasterPosition {virtual MasterCoord mastercoord() const = 0;
}
class MasterCoord: , public MasterPosition {MasterCoord();MasterCoord(double eta,
double xi);double operator()(int i) const;double& operator()(int i);MasterCoord& operator+=(const MasterCoord& other);MasterCoord& operator*=(double factor);
}
MasterCoord operator+(const MasterCoord&, const MasterCoord&) MasterCoord operator-(const MasterCoord&, const MasterCoord&) MasterCoord operator*(double, const MasterCoord&) MasterCoord operator*(const MasterCoord&, double) MasterCoord operator/(const MasterCoord&, double) double cross(const MasterCoord&, const MasterCoord&) double operator%(const MasterCoord&, const MasterCoord&) double dot(const MasterCoord&, const MasterCoord&) double norm2(const MasterCoord&) bool operator==(const MasterCoord&, const MasterCoord&) bool operator<(const MasterCoord&, const MasterCoord&)
Python Synopsis
from oof2.SWIG.engine import mastercoord
class MasterPosition:def mastercoord(self)
class MasterCoord(MasterPosition):def MasterCoord(self, eta, xi)def __getitem__(self, i)def __add__(self, other)def __sub__(self, other)def __mul__(self, factor)def __div__(self, factor)def __cmp__(self, other)
Description
The MasterPosition and
MasterCoord classes represent points in
an Element's
master coordinate space, with coordinates
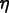and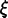 
. Each type of
Element has a standard predetermined
shape in its master space, as shown in Figure 8.14.
Elements are mapped from master space
to physical space, where they have different positions and
geometry. The master space coordinates are useful because the
finite element shape functions have a simple form in master
space coordinates, and because the gauss integration points
have standard positions and weights there. Finite element
calculations are done in master coordinates wherever
possible. The Element class contains
functions that convert coordinates
from master space to physical space, and vice versa.
Figure 8.14. Master Coordinates
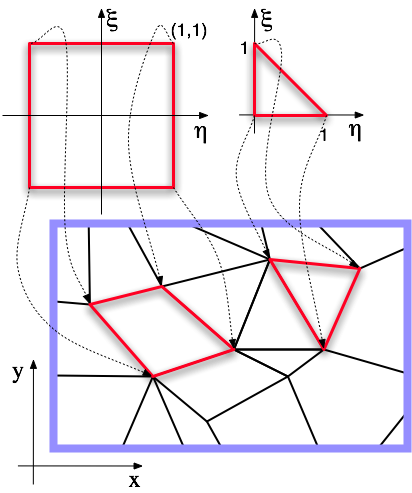
The two plots at the top show the master element geometry in (η, ξ) coordinates, for quads and triangles. The quad is a 2×2 square and the triangle is a right isosceles triangle. The dotted lines show how the master elements might be mapped into physical elements in (x,y) space. Every physical element comes from a different mapping.
The MasterPosition class serves as an
abstract base class for both
MasterCoord and
GaussPoint.
GaussPoint is used for numerical
integration over an Element, and is
derived from both MasterPosition and
Position.
Methods
MasterCoord& mastercoord() const
mastercoord() is a virtual function
in the MasterPosition base class. It
converts any MasterPosition into a
MasterCoord.
MasterCoord(), MasterCoord(double x, double y)
MasterCoords can be constructed by
specifying the components of their location in the master
coordinate space. The default constructor (with no
arguments) puts the point at the origin.
double operator()(int i), __getitem__(i)
The components of a MasterCoord
mc can be retrieved with
mc(i) in C++ or mc[i] in Python.
(The notational inconsistency is historical and
regrettable.) Use i=0 for
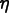and
i=1 for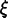 
.
operator+=, operator*, __add__, etc.
A full set of arithmetic operations are provided for
MasterCoords in C++. As with Coords,
a somewhat limited set of operations is available in Python.
This is because doing arithmetic in Python is relatively
inefficient and should be avoided.
double cross(const MasterCoord&, const
MasterCoord&), operator%(const MasterCoord&, const
MasterCoord&)
The cross product of two MasterCoords
a and b can be
computed either by cross(a,b) or by
a%b. Because
MasterCoords are two dimensional vectors,
the cross product is a scalar, not a vector. It's
equivalent to the z-component of a three dimensional cross
product.
|
|
 |
|
| Coord |  |
Point |