The free energy increase due to interfacial energy or surface energy is known as a capilarity effect or the Gibbs-Thompson effect. This is a main driving force that contributes to particle coarsening or "Ostwald Ripening."*
*D.A. Porter and K.E. Easterling, Phase Transformation in Metals and Alloys, 2nd. ed. (1992) pages 46 and 314.
This page describes the famous (sort of) double bubble problem. In this example from Surface Evolver two soapfilms are connected through an imaginary bubble pipe. So, as the user blows air into the pipe, both soapfilms are inflated simultaneously. Can you guess what happens as the volume continues to increase? (Hint: Since I'm asking you this question, it is probably not what you think!)
Here is the system just after the user begins inflating the bubbles. The volume here is 1.1 units:

Here is a plot of the surface area for a symmetric pair of bubbles (blue), an asymemetric pair of bubbles (pink), the surface area for the larger bubble (yellow), and the smaller bubble (red). These are plotted against the total system volume. What do you notice between the blue and pink curves? Where does the divergence in the total system area between the symmetric and asymmetric bubbles begin? (You can click on the graph to get a larger version!)
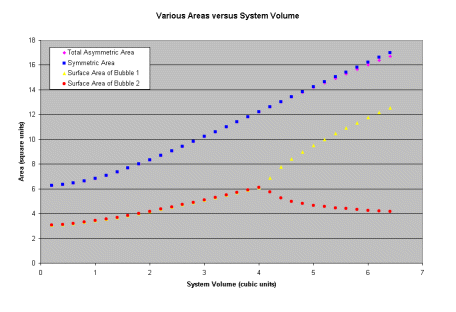
For a total system volume greater than 4.0 units the sum of the surface areas of bubble 1 and 2 is reduced by having one larger and one smaller bubble. The key to understanding Ostwald ripening is that, like the bubbles, each of the individual particles is linked to the other! That is, each particle senses the pressure exerted by each other particle! In the case of bubbles it is the internal pressure of the bubbles, in the case of a metallic system what it the corresponding pressure?
Does this experiment imply that there is a critical volume fraction of particles necessary before Ostwald ripening can initiate?
If you like this page and you are interested in the software that generated the results, please visit Ken Brakke's homepage and try it out for yourself! Thanks Professor Brakke for all your help!