examples.phase.polyxtalCoupled¶

Simultaneously solve the dendritic growth of nuclei and subsequent grain impingement.

To convert a liquid material to a solid, it must be cooled to a temperature below its melting point (known as “undercooling” or “supercooling”). The rate of solidification is often assumed (and experimentally found) to be proportional to the undercooling. Under the right circumstances, the solidification front can become unstable, leading to dendritic patterns. Warren, Kobayashi, Lobkovsky and Carter [13] have described a phase field model (“Allen-Cahn”, “non-conserved Ginsberg-Landau”, or “model A” of Hohenberg & Halperin) of such a system, including the effects of discrete crystalline orientations (anisotropy).

We start with a regular 2D Cartesian mesh

>>> from fipy import  CellVariable, Variable, ModularVariable, Grid2D, TransientTerm, DiffusionTerm, ImplicitSourceTerm, PowerLawConvectionTerm, MatplotlibViewer, Matplotlib2DGridViewer, MultiViewer
>>> from fipy.tools import numerix
>>> dx = dy = 0.025
>>> if __name__ == "__main__":
...     nx = ny = 200
... else:
...     nx = ny = 20
>>> mesh = Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)

and we’ll take fixed timesteps

>>> dt = 5e-4

We consider the simultaneous evolution of a “phase field” variable $\phi$ (taken to be 0 in the liquid phase and 1 in the solid)

>>> phase = CellVariable(name=r'$\phi$', mesh=mesh, hasOld=True)

a dimensionless undercooling $\Delta T$ ( $\Delta T = 0$ at the melting point)

>>> dT = CellVariable(name=r'$\Delta T$', mesh=mesh, hasOld=True)

and an orientation $-\pi < \theta \le \pi$

>>> theta = ModularVariable(name=r'$\theta$', mesh=mesh, hasOld=True)
>>> theta.value = -numerix.pi + 0.0001

The hasOld flag causes the storage of the value of variable from the previous timestep. This is necessary for solving equations with non-linear coefficients or for coupling between PDEs.

The governing equation for the temperature field is the heat flux equation, with a source due to the latent heat of solidification

$\frac{\partial \Delta T}{\partial t} = D_T \nabla^2 \Delta T + \frac{\partial \phi}{\partial t} + c\left(T_0 - T\right)$

>>> DT = 2.25
>>> q = Variable(0.)
>>> T_0 = -0.1
>>> heatEq = (TransientTerm(var=dT)
...           == DiffusionTerm(coeff=DT, var=dT)
...           + TransientTerm(var=phase)
...           + q * T_0 - ImplicitSourceTerm(coeff=q, var=dT))

The governing equation for the phase field is

$\tau_{\phi} \frac{\partial \phi}{\partial t} = \nabla \cdot \mathsf{D} \nabla \phi + \phi ( 1 - \phi ) m ( \phi , \Delta T) - 2 s \phi | \nabla \theta | - \epsilon^2 \phi | \nabla \theta |^2$

where

$m(\phi, \Delta T) = \phi - \frac{1}{2} - \frac{ \kappa_1 }{ \pi } \arctan \left( \kappa_2 \Delta T \right)$

represents a source of anisotropy. The coefficient $\mathsf{D}$ is an anisotropic diffusion tensor in two dimensions

$\mathsf{D} = \alpha^2 \left( 1 + c \beta \right) \left[ \begin{matrix} 1 + c \beta & -c \frac{\partial \beta}{\partial \psi} \\ c \frac{\partial \beta}{\partial \psi} & 1 + c \beta \end{matrix} \right]$

where $\beta = \frac{ 1 - \Phi^2 } { 1 + \Phi^2}$ , $\Phi = \tan \left( \frac{ N } { 2 } \psi \right)$ , $\psi = \theta + \arctan \frac{\partial \phi / \partial y}{\partial \phi / \partial x}$ , $\theta$ is the orientation, and $N$ is the symmetry.

>>> alpha = 0.015
>>> c = 0.02
>>> N = 4.

>>> psi = theta.arithmeticFaceValue + numerix.arctan2(phase.faceGrad[1],
...                                                   phase.faceGrad[0])
>>> Phi = numerix.tan(N * psi / 2)
>>> PhiSq = Phi**2
>>> beta = (1. - PhiSq) / (1. + PhiSq)
>>> DbetaDpsi = -N * 2 * Phi / (1 + PhiSq)
>>> Ddia = (1.+ c * beta)

>>> Doff = c * DbetaDpsi
>>> I0 = Variable(value=((1, 0), (0, 1)))
>>> I1 = Variable(value=((0, -1), (1, 0)))
>>> D = alpha**2 * Ddia * (Ddia * I0 + Doff * I1)

With these expressions defined, we can construct the phase field equation as

>>> tau_phase = 3e-4
>>> kappa1 = 0.9
>>> kappa2 = 20.
>>> epsilon = 0.008
>>> s = 0.01
>>> thetaMag = theta.grad.mag
>>> phaseEq = (TransientTerm(coeff=tau_phase, var=phase)
...            == DiffusionTerm(coeff=D, var=phase)
...            + ImplicitSourceTerm(coeff=((phase - 0.5 - kappa1 / numerix.pi * numerix.arctan(kappa2 * dT))
...                                        * (1 - phase)
...                                        - (2 * s + epsilon**2 * thetaMag) * thetaMag),
...                                 var=phase))

The governing equation for orientation is given by

$P(\epsilon | \nabla \theta |) \tau_{\theta} \phi^2 \frac{\partial \theta}{\partial t} = \nabla \cdot \left[ \phi^2 \left( \frac{s}{| \nabla \theta |} + \epsilon^2 \right) \nabla \theta \right]$

where

$P(w) = 1 - \exp{(-\beta w)} + \frac{\mu}{\epsilon} \exp{(-\beta w)}$

The theta equation is built in the following way. The details for this equation are fairly involved, see J. A. Warren et al.. The main detail is that a source must be added to correct for the discretization of theta on the circle.

>>> tau_theta = 3e-3
>>> mu = 1e3
>>> gamma = 1e3
>>> thetaSmallValue = 1e-6
>>> phaseMod = phase + ( phase < thetaSmallValue ) * thetaSmallValue
>>> beta_theta = 1e5
>>> expo = epsilon * beta_theta * theta.grad.mag
>>> expo = (expo < 100.) * (expo - 100.) + 100.
>>> Pfunc = 1. + numerix.exp(-expo) * (mu / epsilon - 1.)

>>> gradMagTheta = theta.faceGrad.mag
>>> eps = 1. / gamma / 10.
>>> gradMagTheta += (gradMagTheta < eps) * eps
>>> IGamma = (gradMagTheta > 1. / gamma) * (1 / gradMagTheta - gamma) + gamma
>>> v_theta = phase.arithmeticFaceValue * (s * IGamma + epsilon**2)
>>> D_theta = phase.arithmeticFaceValue**2 * (s * IGamma + epsilon**2)

The source term requires the evaluation of the face gradient without the modular operator. thetafaceGradNoMod evaluates the gradient without modular arithmetic.

>>> thetaEq = (TransientTerm(coeff=tau_theta * phaseMod**2 * Pfunc, var=theta)
...            == DiffusionTerm(coeff=D_theta, var=theta)
...            + PowerLawConvectionTerm(coeff=v_theta * (theta.faceGrad - theta.faceGradNoMod), var=phase))

We seed a circular solidified region in the center

>>> x, y = mesh.cellCenters
>>> numSeeds = 10
>>> numerix.random.seed(12345)
>>> for Cx, Cy, orientation in numerix.random.random([numSeeds, 3]):
...     radius = dx * 5.
...     seed = ((x - Cx * nx * dx)**2 + (y - Cy * ny * dy)**2) < radius**2
...     phase[seed] = 1.
...     theta[seed] = numerix.pi * (2 * orientation - 1)

and quench the entire simulation domain below the melting point

>>> dT.setValue(-0.5)

In a real solidification process, dendritic branching is induced by small thermal fluctuations along an otherwise smooth surface, but the granularity of the Mesh is enough “noise” in this case, so we don’t need to explicitly introduce randomness, the way we did in the Cahn-Hilliard problem.

FiPy’s viewers are utilitarian, striving to let the user see something, regardless of their operating system or installed packages, so you the default color scheme of grain orientation won’t be very informative “out of the box”. Because all of Python is accessible and FiPy is object oriented, it is not hard to adapt one of the existing viewers to create a specialized display:

>>> from builtins import zip
>>> if __name__ == "__main__":
...     try:
...         class OrientationViewer(Matplotlib2DGridViewer):
...             def __init__(self, phase, orientation, title=None, limits={}, **kwlimits):
...                 self.phase = phase
...                 Matplotlib2DGridViewer.__init__(self, vars=(orientation,), title=title,
...                                                 limits=limits, colorbar=None, **kwlimits)
...
...                 # make room for non-existent colorbar
...                 # stolen from matplotlib.colorbar.make_axes
...                 # https://github.com/matplotlib/matplotlib/blob
...                 #   /ec1cd2567521c105a451ce15e06de10715f8b54d/lib
...                 #   /matplotlib/colorbar.py#L838
...                 fraction = 0.15
...                 pb = self.axes.get_position(original=True).frozen()
...                 pad = 0.05
...                 x1 = 1.0-fraction
...                 pb1, pbx, pbcb = pb.splitx(x1-pad, x1)
...                 panchor = (1.0, 0.5)
...                 self.axes.set_position(pb1)
...                 self.axes.set_anchor(panchor)
...
...                 # make the gnomon
...                 fig = self.axes.get_figure()
...                 self.gnomon = fig.add_axes([0.85, 0.425, 0.15, 0.15], polar=True)
...                 self.gnomon.set_thetagrids([180, 270, 0, 90],
...                                            [r"$\pm\pi$", r"$-\frac{\pi}{2}$", "$0$", r"$+\frac{\pi}{2}$"],
...                                            frac=1.3)
...                 self.gnomon.set_theta_zero_location("N")
...                 self.gnomon.set_theta_direction(-1)
...                 self.gnomon.set_rgrids([1.], [""])
...                 N = 100
...                 theta = numerix.arange(-numerix.pi, numerix.pi, 2 * numerix.pi / N)
...                 radii = numerix.ones((N,))
...                 bars = self.gnomon.bar(theta, radii, width=2 * numerix.pi / N, bottom=0.0)
...                 colors = self._orientation_and_phase_to_rgb(orientation=numerix.array([theta]), phase=1.)
...                 for c, t, bar in zip(colors[0], theta, bars):
...                     bar.set_facecolor(c)
...                     bar.set_edgecolor(c)
...
...             def _reshape(self, var):
...                 '''return values of var in an 2D array'''
...                 return numerix.reshape(numerix.array(var),
...                                        var.mesh.shape[::-1])[::-1]
...
...             @staticmethod
...             def _orientation_and_phase_to_rgb(orientation, phase):
...                 from matplotlib import colors
...
...                 hsv = numerix.empty(orientation.shape + (3,))
...                 hsv[..., 0] = (orientation / numerix.pi + 1) / 2.
...                 hsv[..., 1] = 1.
...                 hsv[..., 2] = phase
...
...                 return colors.hsv_to_rgb(hsv)
...
...             @property
...             def _data(self):
...                 '''convert phase and orientation to rgb image array
...
...                 orientation (-pi, pi) -> hue (0, 1)
...                 phase (0, 1) -> value (0, 1)
...                 '''
...                 orientation = self._reshape(self.vars[0])
...                 phase = self._reshape(self.phase)
...
...                 return self._orientation_and_phase_to_rgb(orientation, phase)
...
...             def _plot(self):
...                 self.image.set_data(self._data)
...
...         from matplotlib import pyplot
...         pyplot.ion()
...         w, h = pyplot.figaspect(1.)
...         fig = pyplot.figure(figsize=(2*w, h))
...         timer = fig.text(0.1, 0.9, "t = %.3f" % 0, fontsize=18)
...
...         viewer = MultiViewer(viewers=(MatplotlibViewer(vars=dT,
...                                                        cmap=pyplot.cm.hot,
...                                                        datamin=-0.5,
...                                                        datamax=0.5,
...                                                        axes=fig.add_subplot(121)),
...                                       OrientationViewer(phase=phase,
...                                                         orientation=theta,
...                                                         title=theta.name,
...                                                         axes=fig.add_subplot(122))))
...     except ImportError:
...         viewer = MultiViewer(viewers=(Viewer(vars=dT,
...                                              datamin=-0.5,
...                                              datamax=0.5),
...                                       Viewer(vars=phase,
...                                              datamin=0.,
...                                              datamax=1.),
...                                       Viewer(vars=theta,
...                                              datamin=-numerix.pi,
...                                              datamax=numerix.pi)))
...     viewer.plot()

and iterate the solution in time, plotting as we go,

>>> eq = thetaEq & phaseEq & heatEq

>>> if __name__ == "__main__":
...     total_time = 2.
... else:
...     total_time = dt * 10
>>> elapsed = 0.
>>> save_interval = 0.002
>>> save_at = save_interval

>>> while elapsed < total_time:
...     if elapsed > 0.3:
...         q.value = 100
...     phase.updateOld()
...     dT.updateOld()
...     theta.updateOld()
...     eq.solve(dt=dt)
...     elapsed += dt
...     if __name__ == "__main__" and elapsed >= save_at:
...         timer.set_text("t = %.3f" % elapsed)
...         viewer.plot()
...         save_at += save_interval

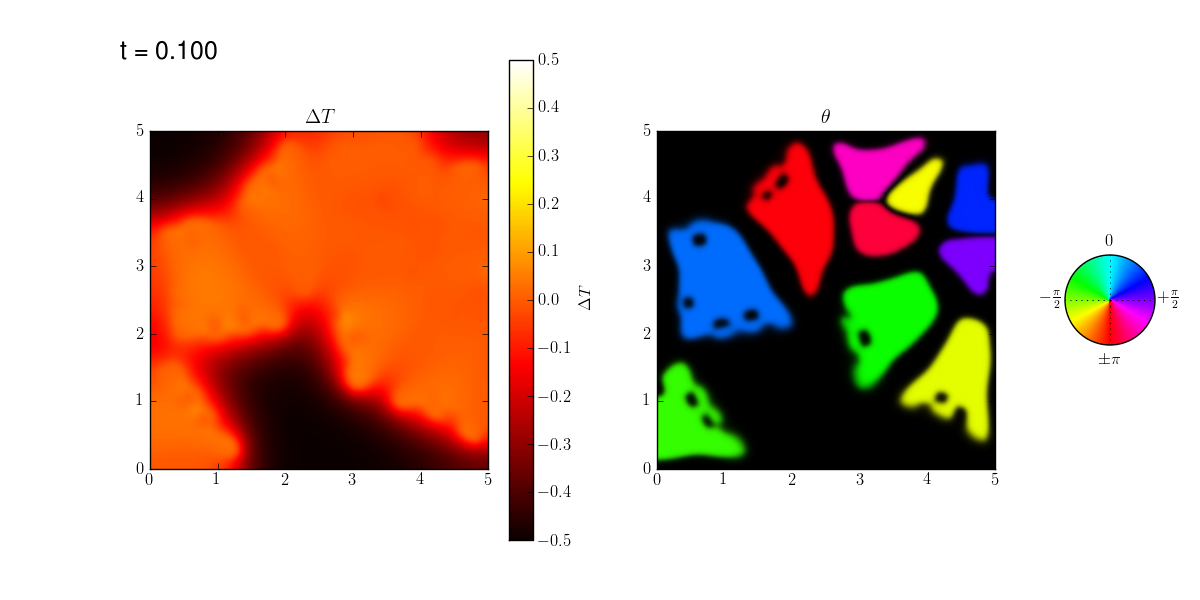
undercooling and grain orientation during solidification of a collection of anisotropic seeds

The non-uniform temperature results from the release of latent heat at the solidifying interface. The dendrite arms grow fastest where the temperature gradient is steepest.

Last updated on Jun 27, 2023. Created using Sphinx 6.2.1.