examples.diffusion.mesh20x20

Solve a two-dimensional diffusion problem in a square domain.

This example solves a diffusion problem and demonstrates the use of applying boundary condition patches.

>>> from fipy import CellVariable, Grid2D, Viewer, TransientTerm, DiffusionTerm
>>> from fipy.tools import numerix

>>> nx = 20
>>> ny = nx
>>> dx = 1.
>>> dy = dx
>>> L = dx * nx
>>> mesh = Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)

We create a CellVariable and initialize it to zero:

>>> phi = CellVariable(name = "solution variable",
...                    mesh = mesh,
...                    value = 0.)

and then create a diffusion equation. This is solved by default with an iterative conjugate gradient solver.

>>> D = 1.
>>> eq = TransientTerm() == DiffusionTerm(coeff=D)

We apply Dirichlet boundary conditions

>>> valueTopLeft = 0
>>> valueBottomRight = 1

to the top-left and bottom-right corners. Neumann boundary conditions are automatically applied to the top-right and bottom-left corners.

>>> X, Y = mesh.faceCenters
>>> facesTopLeft = ((mesh.facesLeft & (Y > L / 2))
...                 | (mesh.facesTop & (X < L / 2)))
>>> facesBottomRight = ((mesh.facesRight & (Y < L / 2))
...                     | (mesh.facesBottom & (X > L / 2)))

>>> phi.constrain(valueTopLeft, facesTopLeft)
>>> phi.constrain(valueBottomRight, facesBottomRight)

We create a viewer to see the results

>>> if __name__ == '__main__':
...     viewer = Viewer(vars=phi, datamin=0., datamax=1.)
...     viewer.plot()

and solve the equation by repeatedly looping in time:

>>> timeStepDuration = 10 * 0.9 * dx**2 / (2 * D)
>>> steps = 10
>>> from builtins import range
>>> for step in range(steps):
...     eq.solve(var=phi,
...              dt=timeStepDuration)
...     if __name__ == '__main__':
...         viewer.plot()

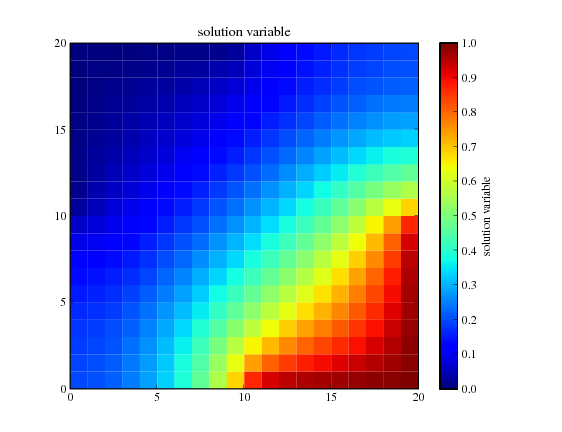
We can test the value of the bottom-right corner cell.

>>> print(numerix.allclose(phi(((L,), (0,))), valueBottomRight, atol = 1e-2))
1

>>> from fipy import input
>>> if __name__ == '__main__':
...     input("Implicit transient diffusion. Press <return> to proceed...")

---

We can also solve the steady-state problem directly

>>> DiffusionTerm().solve(var=phi)
>>> if __name__ == '__main__':
...     viewer.plot()

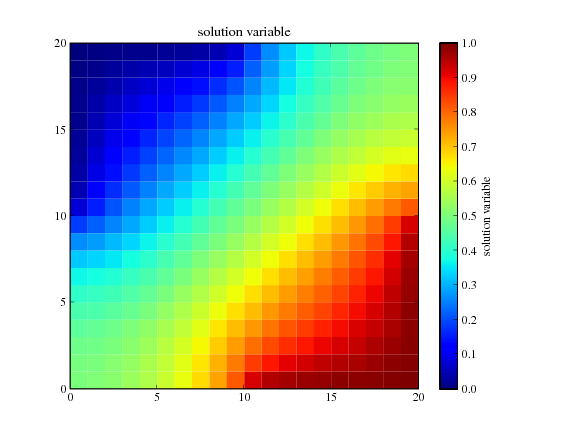
and test the value of the bottom-right corner cell.

>>> print(numerix.allclose(phi(((L,), (0,))), valueBottomRight, atol = 1e-2))
1

>>> from fipy import input
>>> if __name__ == '__main__':
...     input("Implicit steady-state diffusion. Press <return> to proceed...")

Last updated on Jun 27, 2023. Created using Sphinx 6.2.1.