Finite Volume Method

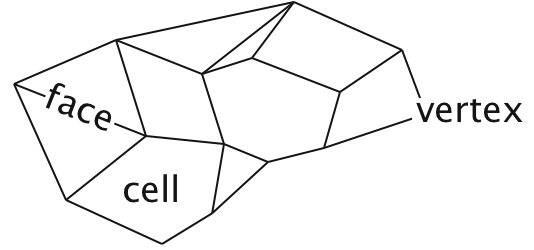
To use the FVM, the solution domain must first be divided into non-overlapping polyhedral elements or cells. A solution domain divided in such a way is generally known as a mesh (as we will see, a Mesh is also a FiPy object). A mesh consists of vertices, faces and cells (see Figure Mesh). In the FVM the variables of interest are averaged over control volumes (CVs). The CVs are either defined by the cells or are centered on the vertices.

../../_images/meshcartoon.png

Mesh

A mesh consists of cells, faces and vertices. For the purposes of FiPy, the divider between two cells is known as a face for all dimensions.

Cell Centered FVM (CC-FVM)

In the CC-FVM the CVs are formed by the mesh cells with the cell center “storing” the average variable value in the CV, (see Figure CV structure for an unstructured mesh). The face fluxes are approximated using the variable values in the two adjacent cells surrounding the face. This low order approximation has the advantage of being efficient and requiring matrices of low band width (the band width is equal to the number of cell neighbors plus one) and thus low storage requirement. However, the mesh topology is restricted due to orthogonality and conjunctionality requirements. The value at a face is assumed to be the average value over the face. On an unstructured mesh the face center may not lie on the line joining the CV centers, which will lead to an error in the face interpolation. FiPy currently only uses the CC-FVM.

Boundary Conditions

The natural boundary condition for CC-FVM is no-flux. For (2), the boundary condition is

\hat{n}\cdot[\vec{u}\phi - (\Gamma_i\nabla)^n] = 0

Vertex Centered FVM (VC-FVM)

In the VC-FVM, the CV is centered around the vertices and the cells are divided into sub-control volumes that make up the main CVs (see Figure CV structure for an unstructured mesh). The vertices “store” the average variable values over the CVs. The CV faces are constructed within the cells rather than using the cell faces as in the CC-FVM. The face fluxes use all the vertex values from the cell where the face is located to calculate interpolations. For this reason, the VC-FVM is less efficient and requires more storage (a larger matrix band width) than the CC-FVM. However, the mesh topology does not have the same restrictions as the CC-FVM. FiPy does not have a VC-FVM capability.

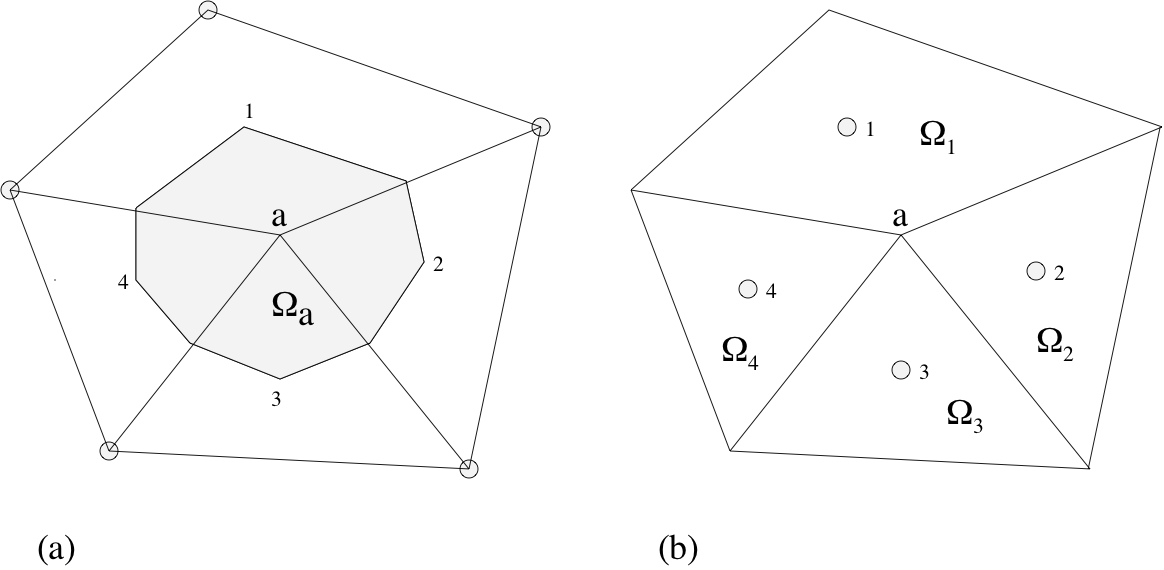
../../_images/vc-cc-fv.png

CV structure for an unstructured mesh

(a) \Omega_a represents a vertex-based CV and (b) \Omega_1, \Omega_2, \Omega_3 and \Omega_4 represent cell centered CVs.

Discretization

The first step in the discretization of Equation (2) using the CC-FVM is to integrate over a CV and then make appropriate approximations for fluxes across the boundary of each CV. In this section, each term in Equation (2) will be examined separately.

Transient Term \partial (\rho \phi) / \partial t

For the transient term, the discretization of the integral \int_V over the volume of a CV is given by

(1)\int_V \frac{\partial (\rho \phi)}{\partial t} dV \simeq \frac{(\rho_{P} \phi_{P} - \rho_{P}^\text{old} \phi_{P}^\text{old}) V_P}{\Delta t}

where \phi_P represents the average value of \phi in a CV centered on a point P and the superscript “\text{old}” represents the previous time-step value. The value V_P is the volume of the CV and \Delta t is the time step size.

This term is represented in FiPy as

>>> TransientTerm(coeff=rho)

Convection Term \nabla \cdot \left( \vec{u} \phi \right)

The discretization for the convection term is given by

(2)\int_V \nabla \cdot (\vec{u} \phi)\,dV &= \int_S (\vec{n} \cdot \vec{u})\phi\,dS \\ &\simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f

where we have used the divergence theorem to transform the integral over the CV volume \int_V into an integral over the CV surface \int_S. The summation over the faces of a CV is denoted by \sum_{f} and A_f is the area of each face. The vector \vec{n} is the normal to the face pointing out of the CV into an adjacent CV centered on point A. When using a first order approximation, the value of \phi_f must depend on the average value in adjacent cell \phi_A and the average value in the cell of interest \phi_P, such that

\phi_f=\alpha_f \phi_P +(1-\alpha_f)\phi_A.

The weighting factor \alpha_f is determined by the convection scheme, described in Numerical Schemes.

This term is represented in FiPy as

>>> <SpecificConvectionTerm>(coeff=u)

where <SpecificConvectionTerm> can be any of CentralDifferenceConvectionTerm, ExponentialConvectionTerm, HybridConvectionTerm, PowerLawConvectionTerm, UpwindConvectionTerm, ExplicitUpwindConvectionTerm, or VanLeerConvectionTerm. The differences between these convection schemes are described in Section Numerical Schemes. The velocity coefficient u must be a rank-1 FaceVariable, or a constant vector in the form of a Python list or tuple, e.g. ((1,), (2,)) for a vector in 2D.

Diffusion Term \nabla \cdot \left( \Gamma_1 \nabla \phi \right)

The discretization for the diffusion term is given by

(3)\int_V \nabla \cdot (\Gamma\nabla\{\ldots\}) dV &= \int_S \Gamma (\vec{n} \cdot \nabla\{\ldots\}) dS \\ &\simeq \sum_f \Gamma_f (\vec{n} \cdot \nabla\{\ldots\})_f A_f

\{\ldots\} indicates recursive application of the specified operation on \phi, depending on the order of the diffusion term. The estimation for the flux, (\vec{n} \cdot \nabla\{\ldots\})_f, is obtained via

(\vec{n} \cdot \nabla\{\ldots\})_f \simeq \frac{\{\ldots\}_A-\{\ldots\}_P}{d_{AP}}

where the value of d_{AP} is the distance between neighboring cell centers. This estimate relies on the orthogonality of the mesh, and becomes increasingly inaccurate as the non-orthogonality increases. Correction terms have been derived to improve this error but are not currently included in FiPy [14].

This term is represented in FiPy as

>>> DiffusionTerm(coeff=Gamma1)

or

>>> ExplicitDiffusionTerm(coeff=Gamma1)

ExplicitDiffusionTerm is provided primarily for illustrative purposes, although examples.diffusion.mesh1D demonstrates its use in Crank-Nicolson time stepping. ImplicitDiffusionTerm is almost always preferred (DiffusionTerm is a synonym for ImplicitDiffusionTerm to reinforce this preference). One can also create an explicit diffusion term with

>>> (Gamma1 * phi.faceGrad).divergence

Higher Order Diffusion

Higher order diffusion expressions, such as \nabla^4 \phi or \nabla \cdot \left( \Gamma_1 \nabla \left( \nabla\cdot\left( \Gamma_2 \nabla \phi\right) \right) \right) for Cahn-Hilliard are represented as

>>> DiffusionTerm(coeff=(Gamma1, Gamma2))

The number of elements supplied for coeff determines the order of the term.

Note

While this multiple-coefficient form is still supported, Coupled and Vector Equations are the recommended approach for higher order expressions.

Source Term

Any term that cannot be written in one of the previous forms is considered a source S_{\phi}. The discretization for the source term is given by,

(4)\int_V S_{\phi}\,dV \simeq S_\phi V_P.

Including any negative dependence of S_\phi on \phi increases solution stability. The dependence can only be included in a linear manner so Equation (4) becomes

V_P (S_0 + S_1 \phi_P),

where S_0 is the source which is independent of \phi and S_1 is the coefficient of the source which is linearly dependent on \phi.

A source term is represented in FiPy essentially as it appears in mathematical form, e.g., 3\kappa^2 + b \sin \theta would be written

>>> 3 * kappa**2 + b * numerix.sin(theta)

Note

Functions like sin() can be obtained from the fipy.tools.numerix module.

Warning

Generally, things will not work as expected if the equivalent function is used from the NumPy or SciPy library.

If, however, the source depends on the variable that is being solved for, it can be advantageous to linearize the source and cast part of it as an implicit source term, e.g., 3\kappa^2 + \phi \sin \theta might be written as

>>> 3 * kappa**2 + ImplicitSourceTerm(coeff=sin(theta))

Linear Equations

The aim of the discretization is to reduce the continuous general equation to a set of discrete linear equations that can then be solved to obtain the value of the dependent variable at each CV center. This results in a sparse linear system that requires an efficient iterative scheme to solve. The iterative schemes available to FiPy are currently encapsulated in the Pysparse and PyTrilinos suites of solvers and include most common solvers such as the conjugate gradient method and LU decomposition.

Combining Equations (1), (2), (3) and (4), the complete discretization for equation (2) can now be written for each CV as

(5)\frac{\rho_{P}(\phi_{P} - \phi_P^\text{old}) V_P}{\Delta t} + & \sum_{f} (\vec{n} \cdot \vec{u})_f A_f \left[\alpha_f \phi_P +\left(1-\alpha_f\right)\phi_A\right] \nonumber \\ = & \sum_f \Gamma_f A_f \frac{(\phi_A-\phi_P)}{d_{AP}} + V_P ( S_0 + S_1 \phi_P ).

Equation (5) is now in the form of a set of linear combinations between each CV value and its neighboring values and can be written in the form

(6)a_P \phi_P = \sum_f a_{A} \phi_{A} + b_P,

where

a_P &= \frac{\rho_P V_P}{\Delta t} + \sum_f (a_{A} + F_f) - V_P S_1, \\ a_{A} &= D_f - ( 1 - \alpha_f ) F_f, \\ b_P &= V_P S_0 + \frac{\rho_P V_P \phi_P^\text{old}}{\Delta t}.

The face coefficients, F_f and D_f, represent the convective strength and diffusive conductance respectively, and are given by

F_f &= A_f ( \vec{u} \cdot \vec{n} )_f, \\ D_f &= \frac{A_f \Gamma_f}{d_{AP}}.

Last updated on Jun 27, 2023. Created using Sphinx 6.2.1.