`terms` Package Documentation¶

This page contains the terms Package documentation.

The `cellTerm` Module¶

class fipy.terms.cellTerm.CellTerm(coeff=1.0)¶: Bases: fipy.terms.term.Term

Attention

This class is abstract. Always create one of its subclasses.

The `centralDiffConvectionTerm` Module¶

class fipy.terms.centralDiffConvectionTerm.CentralDifferenceConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.convectionTerm.ConvectionTerm

This Term represents

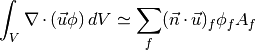
$\int_V \nabla \cdot (\vec{u} \phi)\,dV \simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f$

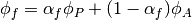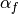where $\phi_f=\alpha_f \phi_P +(1-\alpha_f)\phi_A$ and $\alpha_f$ is calculated using the central differencing scheme. For further details see Numerical Schemes.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `collectedDiffusionTerm` Module¶

The `convectionTerm` Module¶

class fipy.terms.convectionTerm.ConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.faceTerm.FaceTerm

Attention

This class is abstract. Always create one of its subclasses.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `diffusionTerm` Module¶

class fipy.terms.diffusionTerm.DiffusionTerm(coeff=(1.0, ))¶

Bases: fipy.terms.term.Term

This term represents a higher order diffusion term. The order of the term is determined by the number of coeffs, such that:

DiffusionTerm(D1)

represents a typical 2nd-order diffusion term of the form

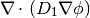
$\nabla\cdot\left(D_1 \nabla \phi\right)$

and:

DiffusionTerm((D1,D2))

represents a 4th-order Cahn-Hilliard term of the form

$\nabla \cdot \left\{ D_1 \nabla \left[ \nabla\cdot\left( D_2 \nabla \phi\right) \right] \right\}$

and so on.

Create a DiffusionTerm.

Parameters :	coeff: Tuple or list of FaceVariables or numbers.

class fipy.terms.diffusionTerm.DiffusionTermNoCorrection(coeff=(1.0, ))¶

Bases: fipy.terms.diffusionTerm.DiffusionTerm

Create a DiffusionTerm.

Parameters :	coeff: Tuple or list of FaceVariables or numbers.

The `equation` Module¶

The `explicitDiffusionTerm` Module¶

class fipy.terms.explicitDiffusionTerm.ExplicitDiffusionTerm(coeff=(1.0, ))¶

Bases: fipy.terms.diffusionTerm.DiffusionTerm

The discretization for the ExplicitDiffusionTerm is given by

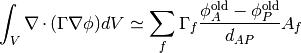
$\int_V \nabla \cdot (\Gamma\nabla\phi) dV \simeq \sum_f \Gamma_f \frac{\phi_A^\text{old}-\phi_P^\text{old}}{d_{AP}} A_f$

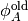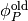where $\phi_A^\text{old}$ and $\phi_P^\text{old}$ are the old values of the variable. The term is added to the RHS vector and makes no contribution to the solution matrix.

Create a DiffusionTerm.

Parameters :	coeff: Tuple or list of FaceVariables or numbers.

The `explicitSourceTerm` Module¶

The `explicitUpwindConvectionTerm` Module¶

class fipy.terms.explicitUpwindConvectionTerm.ExplicitUpwindConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.upwindConvectionTerm.UpwindConvectionTerm

The discretization for this Term is given by

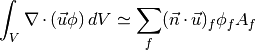
$\int_V \nabla \cdot (\vec{u} \phi)\,dV \simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f$

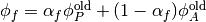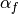where $\phi_f=\alpha_f \phi_P^\text{old} +(1-\alpha_f)\phi_A^\text{old}$ and $\alpha_f$ is calculated using the upwind scheme. For further details see Numerical Schemes.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `exponentialConvectionTerm` Module¶

class fipy.terms.exponentialConvectionTerm.ExponentialConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.convectionTerm.ConvectionTerm

The discretization for this Term is given by

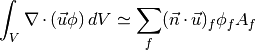
$\int_V \nabla \cdot (\vec{u} \phi)\,dV \simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f$

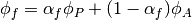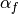where $\phi_f=\alpha_f \phi_P +(1-\alpha_f)\phi_A$ and $\alpha_f$ is calculated using the exponential scheme. For further details see Numerical Schemes.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `faceTerm` Module¶

class fipy.terms.faceTerm.FaceTerm(coeff=1.0)¶: Bases: fipy.terms.term.Term

Attention

This class is abstract. Always create one of its subclasses.

The `hybridConvectionTerm` Module¶

class fipy.terms.hybridConvectionTerm.HybridConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.convectionTerm.ConvectionTerm

The discretization for this Term is given by

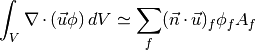
$\int_V \nabla \cdot (\vec{u} \phi)\,dV \simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f$

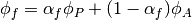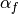where $\phi_f=\alpha_f \phi_P +(1-\alpha_f)\phi_A$ and $\alpha_f$ is calculated using the hybrid scheme. For further details see Numerical Schemes.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `implicitSourceTerm` Module¶

class fipy.terms.implicitSourceTerm.ImplicitSourceTerm(coeff=0.0)¶

Bases: fipy.terms.sourceTerm.SourceTerm

The ImplicitSourceTerm represents

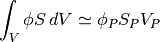
$\int_V \phi S \,dV \simeq \phi_P S_P V_P$

where 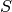$S$ is the coeff value.

The `mulTerm` Module¶

The `nthOrderDiffusionTerm` Module¶

class fipy.terms.nthOrderDiffusionTerm.ExplicitNthOrderDiffusionTerm(coeff)¶: Bases: fipy.terms.explicitDiffusionTerm.ExplicitDiffusionTerm

Attention

This class is deprecated. Use ExplicitDiffusionTerm instead.

class fipy.terms.nthOrderDiffusionTerm.NthOrderDiffusionTerm(coeff)¶: Bases: fipy.terms.diffusionTerm.DiffusionTerm

Attention

This class is deprecated. Use ImplicitDiffusionTerm instead.

The `powerLawConvectionTerm` Module¶

class fipy.terms.powerLawConvectionTerm.PowerLawConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.convectionTerm.ConvectionTerm

The discretization for this Term is given by

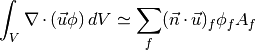
$\int_V \nabla \cdot (\vec{u} \phi)\,dV \simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f$

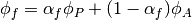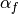where $\phi_f=\alpha_f \phi_P +(1-\alpha_f)\phi_A$ and $\alpha_f$ is calculated using the power law scheme. For further details see Numerical Schemes.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `sourceTerm` Module¶

class fipy.terms.sourceTerm.SourceTerm(coeff=0.0)¶: Bases: fipy.terms.cellTerm.CellTerm

Attention

This class is abstract. Always create one of its subclasses.

The `term` Module¶

class fipy.terms.term.Term(coeff=1.0)¶

Attention

This class is abstract. Always create one of its subclasses.

Create a Term.

Parameters :	coeff: The coefficient for the term. A CellVariable or number. FaceVariable objects are also acceptable for diffusion or convection terms.

cacheMatrix()¶: Informs solve() and sweep() to cache their matrix so that getMatrix() can return the matrix.

cacheRHSvector()¶: Informs solve() and sweep() to cache their right hand side vector so that getRHSvector() can return it.

copy()¶

getDefaultSolver(solver=None, *args, **kwargs)¶

getMatrix()¶: Return the matrix caculated in solve() or sweep(). The cacheMatrix() method should be called before solve() or sweep() to cache the matrix.

getRHSvector()¶: Return the RHS vector caculated in solve() or sweep(). The cacheRHSvector() method should be called before solve() or sweep() to cache the vector.

justResidualVector(var, solver=None, boundaryConditions=(), dt=1.0, underRelaxation=None, residualFn=None)¶

Builds the Term‘s linear system once. This method also recalculates and returns the residual as well as applying under-relaxation.

Parameters :

var: The variable to be solved for. Provides the initial condition, the old value and holds the solution on completion.
solver: The iterative solver to be used to solve the linear system of equations. Defaults to LinearPCGSolver for Pysparse and LinearLUSolver for Trilinos.
boundaryConditions: A tuple of boundaryConditions.
dt: The time step size.
underRelaxation: Usually a value between 0 and 1 or None in the case of no under-relaxation
residualFn: A function that takes var, matrix, and RHSvector arguments used to customize the residual calculation.

residualVectorAndNorm(var, solver=None, boundaryConditions=(), dt=1.0, underRelaxation=None, residualFn=None)¶

Builds the Term‘s linear system once. This method also recalculates and returns the residual as well as applying under-relaxation.

Parameters :

var: The variable to be solved for. Provides the initial condition, the old value and holds the solution on completion.
solver: The iterative solver to be used to solve the linear system of equations. Defaults to LinearPCGSolver for Pysparse and LinearLUSolver for Trilinos.
boundaryConditions: A tuple of boundaryConditions.
dt: The time step size.
underRelaxation: Usually a value between 0 and 1 or None in the case of no under-relaxation
residualFn: A function that takes var, matrix, and RHSvector arguments used to customize the residual calculation.

solve(var, solver=None, boundaryConditions=(), dt=1.0)¶

Builds and solves the Term‘s linear system once. This method does not return the residual. It should be used when the residual is not required.

Parameters :	var: The variable to be solved for. Provides the initial condition, the old value and holds the solution on completion. solver: The iterative solver to be used to solve the linear system of equations. Defaults to LinearPCGSolver for Pysparse and LinearLUSolver for Trilinos. boundaryConditions: A tuple of boundaryConditions. dt: The time step size.

sweep(var, solver=None, boundaryConditions=(), dt=1.0, underRelaxation=None, residualFn=None)¶

Builds and solves the Term‘s linear system once. This method also recalculates and returns the residual as well as applying under-relaxation.

Parameters :

var: The variable to be solved for. Provides the initial condition, the old value and holds the solution on completion.
solver: The iterative solver to be used to solve the linear system of equations. Defaults to LinearPCGSolver for Pysparse and LinearLUSolver for Trilinos.
boundaryConditions: A tuple of boundaryConditions.
dt: The time step size.
underRelaxation: Usually a value between 0 and 1 or None in the case of no under-relaxation
residualFn: A function that takes var, matrix, and RHSvector arguments, used to customize the residual calculation.

The `test` Module¶

The `transientTerm` Module¶

class fipy.terms.transientTerm.TransientTerm(coeff=1.0)¶

Bases: fipy.terms.cellTerm.CellTerm

The TransientTerm represents

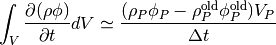
$\int_V \frac{\partial (\rho \phi)}{\partial t} dV \simeq \frac{(\rho_{P} \phi_{P} - \rho_{P}^\text{old} \phi_P^\text{old}) V_P}{\Delta t}$

where 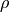$\rho$ is the coeff value.

The following test case verifies that variable coefficients and old coefficient values work correctly. We will solve the following equation

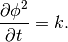
$\frac{ \partial \phi^2 } { \partial t } = k.$

The analytic solution is given by

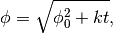
$\phi = \sqrt{ \phi_0^2 + k t },$

where 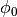$\phi_0$ is the initial value.

>>> phi0 = 1.
>>> k = 1.
>>> dt = 1.
>>> relaxationFactor = 1.5
>>> steps = 2
>>> sweeps = 8

>>> from fipy.meshes.grid1D import Grid1D
>>> mesh = Grid1D(nx = 1)
>>> from fipy.variables.cellVariable import CellVariable
>>> var = CellVariable(mesh = mesh, value = phi0, hasOld = 1)
>>> from fipy.terms.transientTerm import TransientTerm
>>> from fipy.terms.implicitSourceTerm import ImplicitSourceTerm

Relaxation, given by relaxationFactor, is required for a converged solution.

>>> eq = TransientTerm(var) == ImplicitSourceTerm(-relaxationFactor) \
...                            + var * relaxationFactor + k 

A number of sweeps at each time step are required to let the relaxation take effect.

>>> for step in range(steps):
...     var.updateOld()
...     for sweep in range(sweeps):
...         eq.solve(var, dt = dt)

Compare the final result with the analytical solution.

>>> from fipy.tools import numerix
>>> print var.allclose(numerix.sqrt(k * dt * steps + phi0**2))
1

The `upwindConvectionTerm` Module¶

class fipy.terms.upwindConvectionTerm.UpwindConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.convectionTerm.ConvectionTerm

The discretization for this Term is given by

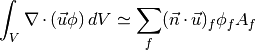
$\int_V \nabla \cdot (\vec{u} \phi)\,dV \simeq \sum_{f} (\vec{n} \cdot \vec{u})_f \phi_f A_f$

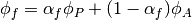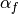where $\phi_f=\alpha_f \phi_P +(1-\alpha_f)\phi_A$ and $\alpha_f$ is calculated using the upwind convection scheme. For further details see Numerical Schemes.

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

The `vanLeerConvectionTerm` Module¶

class fipy.terms.vanLeerConvectionTerm.VanLeerConvectionTerm(coeff=1.0, diffusionTerm=None)¶

Bases: fipy.terms.explicitUpwindConvectionTerm.ExplicitUpwindConvectionTerm

Create a ConvectionTerm object.

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy.variables.cellVariable import CellVariable
>>> from fipy.variables.faceVariable import FaceVariable
>>> m = Grid1D(nx = 2)
>>> cv = CellVariable(mesh = m)
>>> fv = FaceVariable(mesh = m)
>>> vcv = CellVariable(mesh=m, rank=1)
>>> vfv = FaceVariable(mesh=m, rank=1)
>>> __ConvectionTerm(coeff = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = fv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> __ConvectionTerm(coeff = vcv)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = vfv)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.]]), mesh=UniformGrid1D(dx=1.0, nx=2)))
>>> __ConvectionTerm(coeff = (1,))
__ConvectionTerm(coeff=(1,))
>>> from fipy.terms.explicitUpwindConvectionTerm import ExplicitUpwindConvectionTerm
>>> ExplicitUpwindConvectionTerm(coeff = (0,)).solve(var = cv)
>>> ExplicitUpwindConvectionTerm(coeff = 1).solve(var = cv)
Traceback (most recent call last):
    ...
TypeError: The coefficient must be a vector value.
>>> from fipy.meshes.grid2D import Grid2D
>>> m2 = Grid2D(nx=2, ny=1)
>>> cv2 = CellVariable(mesh=m2)
>>> vcv2 = CellVariable(mesh=m2, rank=1)
>>> vfv2 = FaceVariable(mesh=m2, rank=1)
>>> __ConvectionTerm(coeff=vcv2)
__ConvectionTerm(coeff=_ArithmeticCellToFaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> __ConvectionTerm(coeff=vfv2)
__ConvectionTerm(coeff=FaceVariable(value=array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]]), mesh=UniformGrid2D(dx=1.0, nx=2, dy=1.0, ny=1)))
>>> ExplicitUpwindConvectionTerm(coeff = ((0,),(0,))).solve(var=cv2)
>>> ExplicitUpwindConvectionTerm(coeff = (0,0)).solve(var=cv2)

Parameters :	coeff : The Term‘s coefficient value. diffusionTerm : deprecated. The Peclet number is calculated automatically.

Table Of Contents

Previous topic

Next topic

This Page

Contact

`terms` Package Documentation¶

The `cellTerm` Module¶

The `centralDiffConvectionTerm` Module¶

The `collectedDiffusionTerm` Module¶

The `convectionTerm` Module¶

The `diffusionTerm` Module¶

The `equation` Module¶

The `explicitDiffusionTerm` Module¶

The `explicitSourceTerm` Module¶

The `explicitUpwindConvectionTerm` Module¶

The `exponentialConvectionTerm` Module¶

The `faceTerm` Module¶

The `hybridConvectionTerm` Module¶

The `implicitSourceTerm` Module¶

The `mulTerm` Module¶

The `nthOrderDiffusionTerm` Module¶

The `powerLawConvectionTerm` Module¶

The `sourceTerm` Module¶

The `term` Module¶

The `test` Module¶

The `transientTerm` Module¶

The `upwindConvectionTerm` Module¶

The `vanLeerConvectionTerm` Module¶

Navigation

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Contact

terms Package Documentation¶

The cellTerm Module¶

The centralDiffConvectionTerm Module¶

The collectedDiffusionTerm Module¶

The convectionTerm Module¶

The diffusionTerm Module¶

The equation Module¶

The explicitDiffusionTerm Module¶

The explicitSourceTerm Module¶

The explicitUpwindConvectionTerm Module¶

The exponentialConvectionTerm Module¶

The faceTerm Module¶

The hybridConvectionTerm Module¶

The implicitSourceTerm Module¶

The mulTerm Module¶

The nthOrderDiffusionTerm Module¶

The powerLawConvectionTerm Module¶

The sourceTerm Module¶

The term Module¶

The test Module¶

The transientTerm Module¶

The upwindConvectionTerm Module¶

The vanLeerConvectionTerm Module¶

`terms` Package Documentation¶

The `cellTerm` Module¶

The `centralDiffConvectionTerm` Module¶

The `collectedDiffusionTerm` Module¶

The `convectionTerm` Module¶

The `diffusionTerm` Module¶

The `equation` Module¶

The `explicitDiffusionTerm` Module¶

The `explicitSourceTerm` Module¶

The `explicitUpwindConvectionTerm` Module¶

The `exponentialConvectionTerm` Module¶

The `faceTerm` Module¶

The `hybridConvectionTerm` Module¶

The `implicitSourceTerm` Module¶

The `mulTerm` Module¶

The `nthOrderDiffusionTerm` Module¶

The `powerLawConvectionTerm` Module¶

The `sourceTerm` Module¶

The `term` Module¶

The `test` Module¶

The `transientTerm` Module¶

The `upwindConvectionTerm` Module¶

The `vanLeerConvectionTerm` Module¶