We give one example of the usefulness of the variational framework for cases where interfacial energy is discontinuous or non-differentiable. Consider a material composed of many grains, of perhaps differing phases, and surface motion that does NOT conserve the amount of material in a phase or grain. Let the total energy of a system to be the sum of the surface energies of the interfaces plus the bulk energies of the phases:
Gradient flow of surfaces with respect to the mobility-weighted 
inner product on the surface results in normal velocity
where M is a mobility function (probably depending on
normal direction), 
the weighted mean
curvature, and 
is
the bulk energy per unit volume of the phase behind
the interface minus the bulk energy per unit volume of the phase in
front of the interface.
In two dimensions,
force-balance uniquely determines equilibrium angles when all the
Wulff shapes 
have no facets or corners,
but otherwise there can be several different sets of angles.
For example, in the
isotropic equal-energy case triple junctions are at 120 
angles,
and fixing the angle of one interface (and the direction of the
triple junction, in 
) fixes the other two as well.
But when all 
are the same regular octagon (Figure 4.1),
there are three different equilibrium configurations when one segment is held fixed.
* Figure 
. 
The number of triple equilibrium triple junctions is even larger when 
are the same regular hexagon:
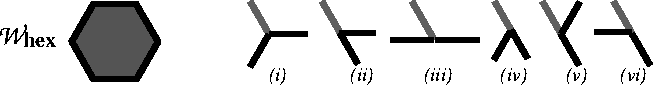
* Figure . 
It can be seen that several different configurations can all have the same surface energy while being the same away from that triple junction but different near it (Figure 4.3)
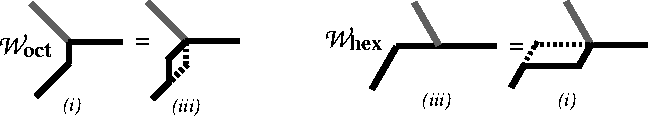
* Figure . 
.
In general,
one can use the variational formulation to determine how such configurations
move. The fundamental idea is that the minimum, for fixed 
, of
occurs at 
, by calculus.
Also, the energy change 
in moving an initial surface S
by the vector field v to a new surface 
is approximately
.
So one can construct a discrete time step flow as follows.
Starting with some initial
configuration S(0) and a time
step ,
set 
to be the minimizer 
of
Then find 
by minimizing starting from 
, etc.
As the time step goes to zero,
the flows should converge to an appropriate limit flow.
Consider surface energy functions for which the Wulff shape W is a polygon in the plane and grain boundaries which are polygonal curves with normal directions that are normals of W. This is a type of numerical discretization where it is the normal directions that are discretized. Two segments of the same interface can be adjacent only if their normal directions are also adjacent in W. And three segments from three different interfaces can meet at a triple junction only if the configuration is force-balanced.
Given a line segment 
in some interface 
in 2D, with normal
and length 
, and with the segment preceding it having
normal 
and that following it having normal 
, the energy change
in moving segment in its normal direction a distance 
is
computed to be 
, where the f are contributions that
derive from the geometry of the corners as illustrated in
Figure 4.4.
and 
[resp. 
]
is 1 if 
follows [resp., 
precedes] 
as a normal of W and is
-1 if precedes [resp., follows] as a normal of
.
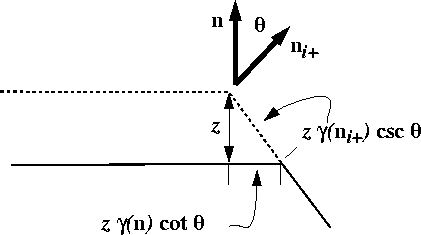
* Figure . v.
For this case, equation 21 can be written as
.
The interpretation of 
in equation 21 comes from the
fact that 
and
and whether the corner is convex with respect to the Wulff shape.
Formulae similar to equation 21 written in terms of the trigonometric
functions can be found in Gibbs [11] for the three-dimensional case.
In the absence of triple junctions, the quantity to be minimized in the time-stepping procedure outlined in equation 19 becomes
Minimizing this over the distances 
to move the segments 
results in
which is Euler's method for motion by weighted mean curvature plus a constant,
since for polygonal Wulff shapes 
.
Observe that the motion of each segment over this
time step is decoupled from the rest: does not depend on any
or 
for 
. (Of course, the motions of the segments
change the lengths, so the lengths at the next time step are indeed
dependent on the motions at the current time step of the neighboring segments.)
In the presence of triple junctions, one might just move a triple junction
from its position 
at time 
to a new position
. One can
then write explicitly the energy as a
function of x and y, and use the relationship
( 
, 
) for each segment
with an endpoint at the triple junction. If none of the coming
into the triple junction
has its other endpoint at another triple junction, then the motion of the three
segments is decoupled from that of all the other
segments but coupled to each other.
If we assume that the at the triple junction have
i= 1,2,3 and that the normals 
each point in a clockwise
direction around the triple point (see Figure 4.5,
then to determine x and y one minimizes
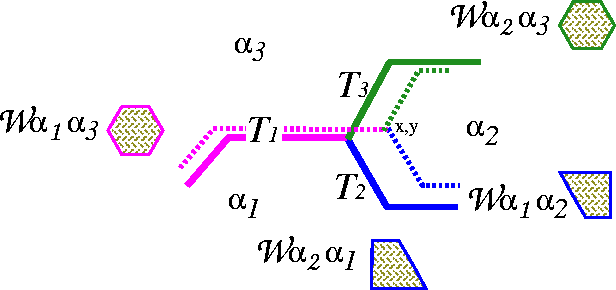
* Figure . 
,
of a grain of type 
embedded within a grain of type 
, is
the central inversion of 
.
Setting the partial derivatives with respect to x and y to zero gives the pair of simultaneous equations
with
The solution is therefore
where 
is clearly positive.
* Figure . 
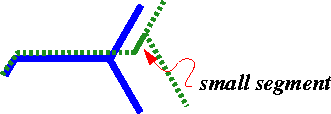
Gradient flow, however, carries the obligation of considering all possible
paths. An obvious alternative motion is to add a small segment
between the endpoint of one of the original segments, say 
,
and the new
position of the triple junction. If the normal direction direction of such
a segment is a normal of 
and is adjacent
to 
in , then we can label that normal direction as
and define 
as before. Now the energy is minimized with
as if had not been at a triple point,
except that there is the constraint
if 
or 
if 
.
To determine x and y, one minimizes
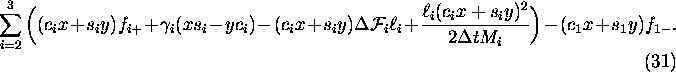
Again, there is a unique solution for the values of x and y; if 
does
not satisfy its constraint, then that says that there is no minimum with
such a small segment being added.
Adding more than one segment to an interface cannot further decrease energy.
Adding it with normal adjacent to but not equal to 
would result in the segment with normal having weighted curvature
of order 
, thereby forcing it up against its constraint
and eliminating the second small segment. Adding it with normal equal to
would result in a configuration with the same energy and not affect
the minimizing position of the triple junction.
One might also try to add new little segments to two of the interfaces. In this case, one finds that now the equations for x and y are dependent; either there are no minimizers within the constraints, or, provided the surface energy functions satisfy a linear relationship with each other, there might be a whole continuum of minimizers. The latter situation has probability zero of holding for surface energy functions corresponding to random grain orientations.
If one tries to add little segments to three of the interfaces, then there is no quadratic term in x and y and hence any minimum occurs at a constraint, proving that one cannot decrease energy by adding three such segments.
The net result is that if the surface energy functions for all the interfaces
do not satisfy that particular relationship, then at most one of the six
possible ways of adding a single small segment satisfies its constraint, and
one cannot add more than one segment.
If one can add one segment while satisfying its constraint,
then that is the overall minimizer; if it doesn't, then the
minimum is obtained by not adding any small segments. In either case,
there results an explicit formula for x and y as well as for each of
the .
In case the surface energy functions for all the interfaces
do satisfy that particular relationship, then this variational
formulation is
inadequate to determine the triple junction position. It is necessary to
replace the inner product, an integral over the surface, by integrals
over the region between the surface and the comparison surface.
This formulation is an extension of that of
[12] and related to, but different from, that of [13],
in which the
mobility critically determines which of the equal-surface-energy minimizers
should be used. (In [14] it was shown that the
formulation of [12] with arbitrary comparison curves gives the
same motion as that obtained by minimizing within the restricted class of
comparisons having the same normal directions as those of
the Wulff shapes, a result that one hopes will carry over to triple junction
motion as formulated here.)
In fact, this integrating-over-regions
is also required in order to handle the case
that all the surface energy functions are zero and only the bulk energy
differences
provide the driving forces (a special case of the particular relationship!),
and it shows how and why the motions
can be different for the assumptions of zero surface energy and vanishingly
small surface energy.
But that is a subject for another paper.
