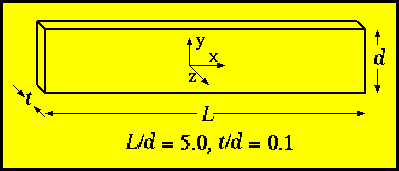µMAG Standard Problem #2
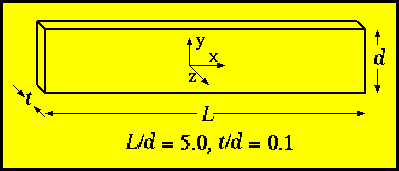
Problem suggested by Tom Koehler, IBM Almaden, ret., and proposed by H.
Neal Bertram, Alfred Liu, and Chris Seberino, Center for Magnetic
Recording Research, University of California at San Diego.
Please send comments to
[email protected] and
join the µMAG discussion e-mail list for
ongoing discussion.
A set of solutions have been submitted.
Specifications
This standard micromagnetic problem includes both magnetostatic and
exchange energies, but has the advantage of only one scaled parameter.
If crystalline anisotropy is neglected and the geometry is fixed,
scaling of the static micromagnetic equations (Brown's equations) yield
a hysteresis loop which depends only on the scaled geometry to the exchange
length when expressed as M/Ms versus
H/Hm, where Hm =
Ms (SI) or 4piMs (cgs emu).
The exchange length is
lex = (A/Km)1/2,
where A is the exchange stiffness constant and
Km is a magnetostatic energy density,
Km =
1/2µ0Ms2
(SI) or 2piMs2 (cgs emu).
The field should be applied in the [1,1,1] direction, approximately
54.74 degrees ( arccos[1/root(3)] ) from each of the coordinate axes.
This field orientation is chosen to avoid potential symmetry breaking
problems.
Geometry:
Let us take a thin film of thickness t, width d,
and length L. We suggest to make the problem virtually 2D
by choosing t/d = 0.1, and to obtain interesting non-uniform
reversal modes, L/d = 5.
Material parameters:
- The magnetostatic exchange length, lex
- Zero magnetocrystalline anisotropy
Desired output for comparison:
Calculated as a function of d/lex, with aspect ratios held constant
at t/d = 0.1 and L/d = 5.0,
- Coercivity (Hc/Hm, the magnitude
of the field at which the projection of the magnetization along the field,
Mx+ My+ Mz,
is zero.)
- Remanence (
Mx/Ms,
My/Ms,
Mz/Ms,
at H = 0)
Please see the µMAG standard problem strategy
page for information on publicizing your results.
Comments:
If we all begin with d/lex = 0.1 then the film will switch
in the plane uniformly with the Stoner-Wohlfarth result for the
coercivity. As we increase d/lex, say to d/lex =
2, simple nonuniform rotation will occur. For d/lex > 2
complex vortex formation will begin to occur and both the remanence and
coercivity will become very small. Also, eventually non uniform
magnetization over the film thickness will occur. We all should agree
when d/lex = 0.1, but it will be interesting to see as we
increase d/lex when our results diverge.
A ``21/2-D'' approach, where the particle is
discretized by a 2-D mesh or grid with 3-D spins, is expected to be sufficient
as long as t is less than lex. For larger particles, a three
dimensional discretization may be necessary.
The results should be shown to be independent of the discretization size.
Site Directory
µMAG organization / NIST CTCMS /
[email protected]
09-FEB-1998