OOF2: The Manual
Name
Quaternion (Quaternion) — The Quaternion representation for 3D orientations. e0 is the cosine of the half-angle of the rotation, and e1 through e3 are the x, y, and z components of the rotation axis times the sine of the half-angle. The rotation brings the crystal axes into coincidence with the lab axes.
Synopsis
Quaternion(e0,e1,e2,e3)
Details
-
Base class:
Orientation -
Parameters:
e0- Cosine of half the rotation angle. Type: A real number.
e1- Rotation axis x-component times sine of half the rotation angle. Type: A real number.
e2- Rotation axis y-component times sine of half the rotation angle. Type: A real number.
e3- Rotation axis z-component times sine of half the rotation angle. Type: A real number.
Description
A Quaternion object represents the
orientation of a three dimensional object, assumed to be a
crystal, in three dimensional space in terms of four parameters
which obey an interesting algebra. This representation of
orientations is not common, but has its roots in the rigid-body
mechanics community.
The parameters correspond to a physical rotation in a similar way
to the Axis convention. Given a
rotation angle
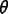 and a normalized rotation axis
and a normalized rotation axis
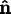 , the quaternion parameters follow
directly:
, the quaternion parameters follow
directly:
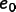 is the cosine of half the
rotation angle, and
is the cosine of half the
rotation angle, and
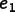 ,
,
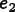 ,
and
,
and
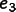 are,
respectively, the x, y, and z components of
are,
respectively, the x, y, and z components of
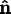 multiplied by the sine of half the rotation angle.
multiplied by the sine of half the rotation angle.
As in the case of the Axis
convention, the specified rotation brings the crystalline
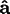 ,
,
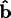 , and
, and
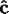 axes into coincidence with the laboratory (or
screen) axes
axes into coincidence with the laboratory (or
screen) axes
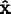 ,
,
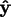 , and
, and
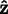 respectively. The
components of
respectively. The
components of
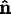 are preserved by this rotation, and so may be specified in either
the crystalline or laboratory coordinate system.
are preserved by this rotation, and so may be specified in either
the crystalline or laboratory coordinate system.



