The same properties for norms and inner products on vectors apply to norms on fields. What does the magnitude of a function mean? What does it mean for a function to be near zero?
There are an infinite number of inner products and norms on fields.
A common choice is to sum the point-wise multiplication of two fields over
a domain 
:
this is the definition of the 
inner product and norm
(functions defined
on a domain with an inner product make up a Hilbert space).
The norm is what is minimized in a parametric least squares fit of a
function to data.
If f and g have integral zero (which can be produced by subtracting of
their averages),
then the norm is a measure of `how far the function is from zero.' For the
rest of this section, all functions assumed to have integral zero.
However, our notion of the distance of a function from zero
may depend on the physical context.
For example, consider the function defined on the periodic domain 
:
which is plotted in figure 2.1
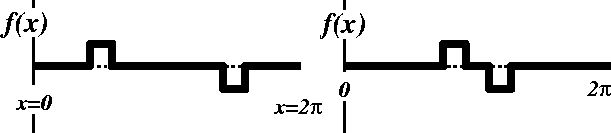
* Figure 
. 
With the norm, 
is independent of 
in
Fig. 2.1; this is reasonable
if ``stuff'' need not flow from one bump to another.
However, if flow is required then the norm is not a useful measure of
the
distance of the function from zero.
The 
(called `H minus one') norm is
particularly useful for diffusive type processes in which there is a
conservation law.
where 
is the solution to the Poisson PDE:
.
As a result the set of functions in inner products is limited to
those with integral 0, and thus is a prime candidate for
variables that are conserved.
It may be helpful to visualize as the steady state
concentration
profile for a mass source density given by 
; then the
norm is the norm of the flux density
.
The natural inner product for is:
We examine how the inner product behaves on the functions
defined in Figure 2.1, by integrating the
function twice to get :
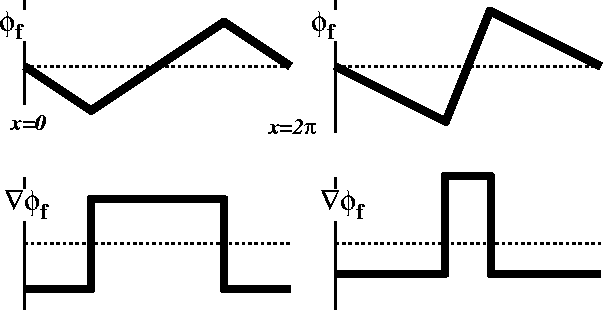
* Figure . and 
for the two
functions in Figure 2.1 in the limit of small 
.
If the norm of f is now plotted as a function of in the limit of
small , we get Figure 2.3.
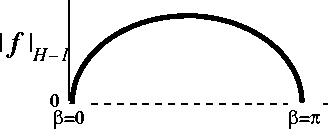
* Figure . 
norm of the function in Figure
2.1
as a function of the bump separation in the limit of small :
.
This illustrates how the magnitude of the function
increases with how much the system must diffuse to reach a uniform
value.
The inner product can be written in a more convenient form, by noting
that
and using the divergence theorem:
where the integral at the boundary is
assumed to be zero
and the operator
is the `inverse Laplacian.' The last form is directly
usable for finding the gradient flow for f.
To see how the inner product is related to the functional norm,
let F be the total free energy of a system with a
free energy density which can be written a function of position, concentration
and concentration
gradients,
at time t=0: 
.
With a flow field, 
, the total free energy as a function of time is
approximately
F(f + vt)
for small t>0.
The initial rate of change of F is:
where 
is the variational derivative of F-the
left-hand-side of Euler's
Equation from variational calculus[5]
from using the divergence theorem to remove derivatives
of v in the volume integral,
assuming the boundary integral is zero.
Again, 
will depend on the choice of the inner product.
The integral over the boundary 
usually vanishes identically, either because admissible
flows v vanish on (Dirichlet conditions), or
because the function g, which depends on derivatives of f with
respect to its gradient and higher order-derivatives, vanishes (Neumann
conditions).
Since the inner product depends on the rate of change, it is natural to
locally `weight' these inner products with some
constant or function 
representing the mobility.
For example in mobility weighting,
a function with a `bump' in a region of high mobility
is closer to zero than it would be if the bump is a region
of low mobility.
Thus the inner product is usually modified to
and the inner product modified to
We now show how standard evolutions result from doing gradient flows with these inner products.
