numMesh Package Documentation

This page contains the numMesh Package documentation.

The cell Module

class fipy.meshes.numMesh.cell.Cell(mesh, id)

getCenter()

getID()

getMesh()

getNormal(index)

The cylindricalGrid1D Module

1D Mesh

class fipy.meshes.numMesh.cylindricalGrid1D.CylindricalGrid1D(dx=1.0, nx=None, origin=(0, ), overlap=2)

Bases: fipy.meshes.numMesh.grid1D.Grid1D

Creates a 1D cylindrical grid mesh.

>>> mesh = CylindricalGrid1D(nx = 3)
>>> print mesh.getCellCenters()
[[ 0.5  1.5  2.5]]

>>> mesh = CylindricalGrid1D(dx = (1, 2, 3))
>>> print mesh.getCellCenters()
[[ 0.5  2.   4.5]]

>>> mesh = CylindricalGrid1D(nx = 2, dx = (1, 2, 3))
Traceback (most recent call last):
...
IndexError: nx != len(dx)

>>> mesh = CylindricalGrid1D(nx=2, dx=(1., 2.)) + ((1.,),)
>>> print mesh.getCellCenters()
[[ 1.5  3. ]]
>>> from fipy.tools import parallel
>>> print parallel.procID > 0  or numerix.allclose(mesh.getCellVolumes(), (1.5, 6))
True

getVertexCoords()

The cylindricalGrid2D Module

2D rectangular Mesh

class fipy.meshes.numMesh.cylindricalGrid2D.CylindricalGrid2D(dx=1.0, dy=1.0, nx=None, ny=None, origin=((0.0, ), (0.0, )), overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.grid2D.Grid2D

Creates a 2D cylindrical grid mesh with horizontal faces numbered first and then vertical faces.

getCellCenters()

getCellVolumes()

getFaceCenters()

getVertexCoords()

The cylindricalUniformGrid1D Module

1D Mesh

class fipy.meshes.numMesh.cylindricalUniformGrid1D.CylindricalUniformGrid1D(dx=1.0, nx=1, origin=(0, ), overlap=2)

Bases: fipy.meshes.numMesh.uniformGrid1D.UniformGrid1D

Creates a 1D cylindrical grid mesh.

>>> mesh = CylindricalUniformGrid1D(nx = 3)
>>> print mesh.getCellCenters()
[[ 0.5  1.5  2.5]]

getCellVolumes()

The cylindricalUniformGrid2D Module

2D cylindrical rectangular Mesh with constant spacing in x and constant spacing in y

class fipy.meshes.numMesh.cylindricalUniformGrid2D.CylindricalUniformGrid2D(dx=1.0, dy=1.0, nx=1, ny=1, origin=((0, ), (0, )), overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.uniformGrid2D.UniformGrid2D

Creates a 2D cylindrical grid in the radial and axial directions, appropriate for axial symmetry.

getCellVolumes()

The face Module

class fipy.meshes.numMesh.face.Face(mesh, id)

Face within a Mesh

Face objects are bounded by Vertex objects. Face objects separate Cell objects.

Face is initialized by Mesh

Parameters :

• mesh: the Mesh that contains this Face
• id: a unique identifier

getArea()

getCellID(index=0)

Return the id of the specified Cell on one side of this Face.

getCenter()

Return the coordinates of the Face center.

getID()

getMesh()

The gmshExport Module

This module takes a FiPy mesh and creates a mesh file that can be opened in Gmsh.

exception fipy.meshes.numMesh.gmshExport.MeshExportError

Bases: exceptions.Exception

fipy.meshes.numMesh.gmshExport.exportAsMesh(mesh, filename)

The gmshImport Module

This module takes a Gmsh output file (.msh) and converts it into a FiPy mesh. This currently supports triangular and tetrahedral meshes only.

Gmsh generates unstructured meshes, which may contain a significant amount of non-orthogonality and it is very difficult to directly control the amount of non-orthogonality simply by manipulating Gmsh parameters. Therefore, it is necessary to take into account the possibility of errors arising due to the non-orthogonality of the mesh. To test the degree of error, an experiment was conducted using a simple 1D diffusion problem with constant diffusion coefficients and boundary conditions as follows: fixed value of 0 on the left side, fixed value of 1 on the right side, and a fixed flux of 0 on the top and bottom sides. The analytical solution is clearly a uniform gradient going from left to right. this problem was implemented using a Cartesian Grid2D mesh with each interior vertex displaced a short distance in a random direction to create non-orthogonality. Then the root-mean-square error was plotted against the root-mean-square non-orthogonality. The error in each cell was calculated by simply subtracting the analytical solution at each cell center from the calculated value for that cell. The non-orthogonality in each cell is the average, weighted by face area, of the sines of the angles between the face normals and the line segments joining the cells. Thus, the non-orthogonality of a cell can range from 0 (every face is orthogonal to its corresponding cell-to-cell line segment) to 1 (only possible in a degenerate case). This test was run using 500 separate 20x20 meshes and 500 separate 10x10 meshes, each with the interior vertices moved different amounts so as to created different levels of non-orthogonality. The results are shown below.

Results for 20x20 mesh:

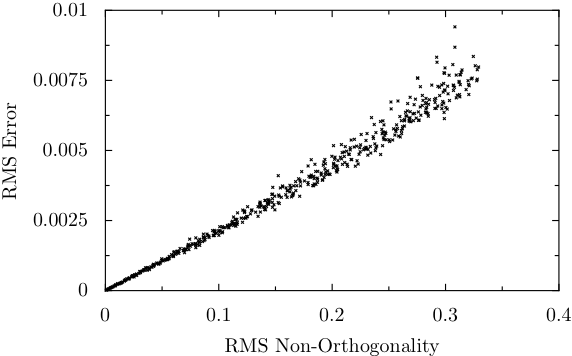
Results for 10x10 mesh:

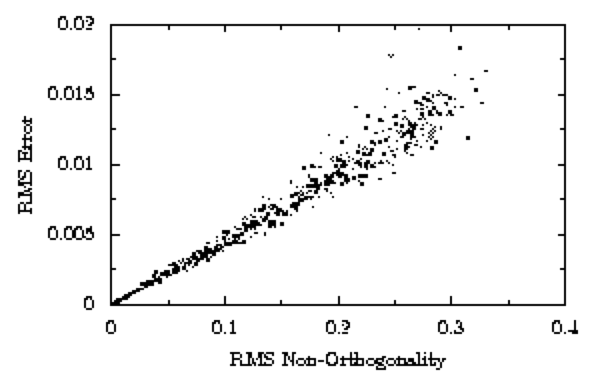
It is clear from the graphs that finer meshes decrease the error due to non-orthogonality, and that even with a reasonably coarse mesh the error is quite low. However, note that this test is only for a simple 1D diffusion problem with a constant diffusion coefficient, and it is unknown whether the results will be significantly different with more complicated problems.

Test cases:

>>> newmesh = GmshImporter3D('fipy/meshes/numMesh/testgmsh.msh')
>>> print newmesh.getVertexCoords()
[[ 0.   0.5  1.   0.5  0.5]
 [ 0.   0.5  0.   1.   0.5]
 [ 0.   1.   0.   0.   0.5]]

>>> print newmesh._getFaceVertexIDs()
[[2 4 4 4 3 4 4 3 4 3]
 [1 1 2 2 1 3 3 2 3 2]
 [0 0 0 1 0 0 1 0 2 1]]

>>> print newmesh._getCellFaceIDs()
[[0 4 7 9]
 [1 1 2 3]
 [2 5 5 6]
 [3 6 8 8]]

>>> mesh = GmshImporter2DIn3DSpace('fipy/meshes/numMesh/GmshTest2D.msh')
>>> print mesh.getVertexCoords()
[[ 0.   1.   0.5  0.   1.   0.5  0.   1. ]
 [ 0.   0.   0.5  1.   1.   1.5  2.   2. ]
 [ 0.   0.   0.   0.   0.   0.   0.   0. ]]

>>> mesh = GmshImporter2D('fipy/meshes/numMesh/GmshTest2D.msh')
>>> print mesh.getVertexCoords()
[[ 0.   1.   0.5  0.   1.   0.5  0.   1. ]
 [ 0.   0.   0.5  1.   1.   1.5  2.   2. ]]

>>> print mesh._getFaceVertexIDs()
[[2 0 1 0 3 1 4 4 3 5 3 6 5 7 7]
 [0 1 2 3 2 4 2 3 5 4 6 5 7 4 6]]

>>> print (mesh._getCellFaceIDs() == [[0, 0, 2, 7, 7, 8, 12, 14],
...                                   [1, 3, 5, 4, 8, 10, 13, 11],
...                                   [2, 4, 6, 6, 9, 11, 9, 12]]).flatten().all()
True

The following test case is to test the handedness of the mesh to check it does not return negative volumes. Firstly we set up a list with tuples of strings to be read by gmsh. The list provide instuctions to gmsh to form a circular mesh.

>>> cellSize = 0.7
>>> radius = 1.
>>> lines = ['cellSize = ' + str(cellSize) + ';\n',
...           'radius = ' + str(radius) + ';\n',
...           'Point(1) = {0, 0, 0, cellSize};\n',
...           'Point(2) = {-radius, 0, 0, cellSize};\n',
...           'Point(3) = {0, radius, 0, cellSize};\n',
...           'Point(4) = {radius, 0, 0, cellSize};\n',
...           'Point(5) = {0, -radius, 0, cellSize};\n',
...           'Circle(6) = {2, 1, 3};\n',
...           'Circle(7) = {3, 1, 4};\n',
...           'Circle(8) = {4, 1, 5};\n',
...           'Circle(9) = {5, 1, 2};\n',
...           'Line Loop(10) = {6, 7, 8, 9} ;\n',
...           'Plane Surface(11) = {10};\n']

Check that the sign of the mesh volumes is correct

>>> mesh = GmshImporter2D(lines)
>>> print mesh.getCellVolumes()[0] > 0
1

Reverse the handedness of the mesh and check the sign

>>> lines[7:12] = ['Circle(6) = {3, 1, 2};\n',
...                'Circle(7) = {4, 1, 3};\n',
...                'Circle(8) = {5, 1, 4};\n',
...                'Circle(9) = {2, 1, 5};\n',
...                'Line Loop(10) = {9, 8, 7, 6};\n',]

>>> mesh = GmshImporter2D(lines)
>>> print mesh.getCellVolumes()[0] > 0
1

class fipy.meshes.numMesh.gmshImport.GmshImporter2D(arg, coordDimensions=2)

Bases: fipy.meshes.numMesh.mesh2D.Mesh2D

getCellVolumes()

class fipy.meshes.numMesh.gmshImport.GmshImporter2DIn3DSpace(arg)

Bases: fipy.meshes.numMesh.gmshImport.GmshImporter2D

class fipy.meshes.numMesh.gmshImport.GmshImporter3D(arg)

Bases: fipy.meshes.numMesh.mesh.Mesh

>>> mesh = GmshImporter3D('fipy/meshes/numMesh/testgmsh.msh')

getCellVolumes()

exception fipy.meshes.numMesh.gmshImport.MeshImportError

Bases: exceptions.Exception

class fipy.meshes.numMesh.gmshImport.MshFile(arg)

getFilename()

remove()

The grid1D Module

1D Mesh

class fipy.meshes.numMesh.grid1D.Grid1D(dx=1.0, nx=None, overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.mesh1D.Mesh1D

Creates a 1D grid mesh.

>>> mesh = Grid1D(nx = 3)
>>> print mesh.getCellCenters()
[[ 0.5  1.5  2.5]]

>>> mesh = Grid1D(dx = (1, 2, 3))
>>> print mesh.getCellCenters()
[[ 0.5  2.   4.5]]

>>> mesh = Grid1D(nx = 2, dx = (1, 2, 3))
Traceback (most recent call last):
...
IndexError: nx != len(dx)

getDim()

getPhysicalShape()

Return physical dimensions of Grid1D.

getScale()

getShape()

The grid2D Module

2D rectangular Mesh

class fipy.meshes.numMesh.grid2D.Grid2D(dx=1.0, dy=1.0, nx=None, ny=None, overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.mesh2D.Mesh2D

Creates a 2D grid mesh with horizontal faces numbered first and then vertical faces.

getPhysicalShape()

Return physical dimensions of Grid2D.

getScale()

getShape()

The grid3D Module

class fipy.meshes.numMesh.grid3D.Grid3D(dx=1.0, dy=1.0, dz=1.0, nx=None, ny=None, nz=None, overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.mesh.Mesh

3D rectangular-prism Mesh

X axis runs from left to right. Y axis runs from bottom to top. Z axis runs from front to back.

Numbering System:

Vertices: Numbered in the usual way. X coordinate changes most quickly, then Y, then Z.

Cells: Same numbering system as vertices.

Faces: XY faces numbered first, then XZ faces, then YZ faces. Within each subcategory, it is numbered in the usual way.

getPhysicalShape()

Return physical dimensions of Grid3D.

getScale()

getShape()

The mesh Module

class fipy.meshes.numMesh.mesh.Mesh(vertexCoords, faceVertexIDs, cellFaceIDs, communicator=<fipy.tools.serialCommWrapper.SerialCommWrapper object at 0x107927590>)

Bases: fipy.meshes.common.mesh.Mesh

Generic mesh class using numerix to do the calculations

Meshes contain cells, faces, and vertices.

This is built for a non-mixed element mesh.

faceVertexIds and cellFacesIds must be padded with minus ones.

getExteriorFaces()

Return only the faces that have one neighboring cell.

getFaceCellIDs()

getFaceCenters()

getInteriorFaces()

Return only the faces that have two neighboring cells.

getVTKCellDataSet()

Returns a TVTK DataSet representing the cells of this mesh

getVTKFaceDataSet()

Returns a TVTK DataSet representing the face centers of this mesh

getVertexCoords()

exception fipy.meshes.numMesh.mesh.MeshAdditionError

Bases: exceptions.Exception

The mesh1D Module

Generic mesh class using numerix to do the calculations

Meshes contain cells, faces, and vertices.

This is built for a non-mixed element mesh.

class fipy.meshes.numMesh.mesh1D.Mesh1D(vertexCoords, faceVertexIDs, cellFaceIDs, communicator=<fipy.tools.serialCommWrapper.SerialCommWrapper object at 0x107927590>)

Bases: fipy.meshes.numMesh.mesh.Mesh

faceVertexIds and cellFacesIds must be padded with minus ones.

The mesh2D Module

Generic mesh class using numerix to do the calculations

Meshes contain cells, faces, and vertices.

This is built for a non-mixed element mesh.

class fipy.meshes.numMesh.mesh2D.Mesh2D(vertexCoords, faceVertexIDs, cellFaceIDs, communicator=<fipy.tools.serialCommWrapper.SerialCommWrapper object at 0x107927590>)

Bases: fipy.meshes.numMesh.mesh.Mesh

faceVertexIds and cellFacesIds must be padded with minus ones.

extrude(extrudeFunc=<function <lambda> at 0x1080a6aa0>, layers=1)

This function returns a new 3D mesh. The 2D mesh is extruded using the extrudeFunc and the number of layers.

Parameters :

• extrudeFunc: function that takes the vertex coordinates and returns the displaced values
• layers: the number of layers in the extruded mesh (number of times extrudeFunc will be called)

>>> from fipy.meshes.grid2D import Grid2D
>>> print Grid2D(nx=2,ny=2).extrude(layers=2).getCellCenters()
[[ 0.5  1.5  0.5  1.5  0.5  1.5  0.5  1.5]
 [ 0.5  0.5  1.5  1.5  0.5  0.5  1.5  1.5]
 [ 0.5  0.5  0.5  0.5  1.5  1.5  1.5  1.5]]

>>> from fipy.meshes.tri2D import Tri2D
>>> print Tri2D().extrude(layers=2).getCellCenters()
[[ 0.83333333  0.5         0.16666667  0.5         0.83333333  0.5
   0.16666667  0.5       ]
 [ 0.5         0.83333333  0.5         0.16666667  0.5         0.83333333
   0.5         0.16666667]
 [ 0.5         0.5         0.5         0.5         1.5         1.5         1.5
   1.5       ]]

The periodicGrid1D Module

Peridoic 1D Mesh

class fipy.meshes.numMesh.periodicGrid1D.PeriodicGrid1D(dx=1.0, nx=None)

Bases: fipy.meshes.numMesh.grid1D.Grid1D

>>> from fipy import numerix
>>> from fipy.tools import parallel

Creates a Periodic grid mesh.

>>> mesh = PeriodicGrid1D(dx = (1, 2, 3))

>>> print (parallel.procID > 0 
...        or numerix.allclose(numerix.nonzero(mesh.getExteriorFaces())[0], 
...                            [3]))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh.getFaceCellIDs().filled(-999),
...                            [[2, 0, 1, 2],
...                             [0, 1, 2, -999]]))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getCellDistances(),
...                            [ 2., 1.5, 2.5, 1.5]))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getCellToCellDistances(),
...                            [[ 2.,   1.5,  2.5],
...                             [ 1.5,  2.5,  2. ]]))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getFaceNormals(),
...                            [[ 1.,  1.,  1.,  1.]]))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getCellVertexIDs(),
...                            [[1, 2, 2],
...                             [0, 1, 0]]))
True

getCellCenters()

The periodicGrid2D Module

2D periodic rectangular Mesh

class fipy.meshes.numMesh.periodicGrid2D.PeriodicGrid2D(dx=1.0, dy=1.0, nx=None, ny=None)

Bases: fipy.meshes.numMesh.grid2D.Grid2D

Creates a periodic2D grid mesh with horizontal faces numbered first and then vertical faces. Vertices and cells are numbered in the usual way.

>>> from fipy import numerix
>>> from fipy.tools import parallel

>>> mesh = PeriodicGrid2D(dx = 1., dy = 0.5, nx = 2, ny = 2)

>>> print (parallel.procID > 0 or 
...        numerix.allclose(numerix.nonzero(mesh.getExteriorFaces())[0],
...                         [ 4,  5,  8, 11]))
True

>>> print (parallel.procID > 0 or 
...        numerix.allclose(mesh.getFaceCellIDs().filled(-1),
...                         [[2, 3, 0, 1, 2, 3, 1, 0, 1, 3, 2, 3],
...                          [0, 1, 2, 3, -1, -1, 0, 1, -1, 2, 3, -1]]))
True

>>> print (parallel.procID > 0 or 
...        numerix.allclose(mesh._getCellDistances(),
...                         [ 0.5, 0.5, 0.5, 0.5, 0.25, 0.25, 1., 1., 0.5, 1., 1., 0.5]))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getCellFaceIDs(),
...                            [[0, 1, 2, 3],
...                             [7, 6, 10, 9],
...                             [2, 3, 0, 1],
...                             [6, 7, 9, 10]]))
True

>>> print (parallel.procID > 0 or 
...        numerix.allclose(mesh._getCellToCellDistances(),
...                         [[ 0.5, 0.5, 0.5, 0.5],
...                          [ 1., 1., 1., 1. ],
...                          [ 0.5, 0.5, 0.5, 0.5],
...                          [ 1., 1., 1., 1. ]]))
True

>>> normals = [[0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1],
...            [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0]]

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getFaceNormals(), normals))
True

>>> print (parallel.procID > 0 
...        or numerix.allclose(mesh._getCellVertexIDs(),
...                            [[4, 5, 7, 8],
...                             [3, 4, 6, 7],
...                             [1, 2, 4, 5],
...                             [0, 1, 3, 4]]))
True

class fipy.meshes.numMesh.periodicGrid2D.PeriodicGrid2DLeftRight(dx=1.0, dy=1.0, nx=None, ny=None)

Bases: fipy.meshes.numMesh.periodicGrid2D.PeriodicGrid2D

class fipy.meshes.numMesh.periodicGrid2D.PeriodicGrid2DTopBottom(dx=1.0, dy=1.0, nx=None, ny=None)

Bases: fipy.meshes.numMesh.periodicGrid2D.PeriodicGrid2D

The skewedGrid2D Module

class fipy.meshes.numMesh.skewedGrid2D.SkewedGrid2D(dx=1.0, dy=1.0, nx=None, ny=1, rand=0)

Bases: fipy.meshes.numMesh.mesh2D.Mesh2D

Creates a 2D grid mesh with horizontal faces numbered first and then vertical faces. The points are skewed by a random amount (between rand and -rand) in the X and Y directions.

getPhysicalShape()

Return physical dimensions of Grid2D.

getScale()

getShape()

The test Module

Test numeric implementation of the mesh

The tri2D Module

class fipy.meshes.numMesh.tri2D.Tri2D(dx=1.0, dy=1.0, nx=1, ny=1)

Bases: fipy.meshes.numMesh.mesh2D.Mesh2D

This class creates a mesh made out of triangles. It does this by starting with a standard Cartesian mesh (Grid2D) and dividing each cell in that mesh (hereafter referred to as a ‘box’) into four equal parts with the dividing lines being the diagonals.

Creates a 2D triangular mesh with horizontal faces numbered first then vertical faces, then diagonal faces. Vertices are numbered starting with the vertices at the corners of boxes and then the vertices at the centers of boxes. Cells on the right of boxes are numbered first, then cells on the top of boxes, then cells on the left of boxes, then cells on the bottom of boxes. Within each of the ‘sub-categories’ in the above, the vertices, cells and faces are numbered in the usual way.

Parameters :

• dx, dy: The X and Y dimensions of each ‘box’. If dx <> dy, the line segments connecting the cell centers will not be orthogonal to the faces.
• nx, ny: The number of boxes in the X direction and the Y direction. The total number of boxes will be equal to nx * ny, and the total number of cells will be equal to 4 * nx * ny.

getPhysicalShape()

Return physical dimensions of Grid2D.

getScale()

getShape()

The uniformGrid1D Module

1D Mesh

class fipy.meshes.numMesh.uniformGrid1D.UniformGrid1D(dx=1.0, nx=1, origin=(0, ), overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.grid1D.Grid1D

Creates a 1D grid mesh.

>>> mesh = UniformGrid1D(nx = 3)
>>> print mesh.getCellCenters()
[[ 0.5  1.5  2.5]]

getCellVolumes()

getFaceCellIDs()

getFaceCenters()

getInteriorFaces()

getVertexCoords()

The uniformGrid2D Module

2D rectangular Mesh with constant spacing in x and constant spacing in y

class fipy.meshes.numMesh.uniformGrid2D.UniformGrid2D(dx=1.0, dy=1.0, nx=1, ny=1, origin=((0, ), (0, )), overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.grid2D.Grid2D

Creates a 2D grid mesh with horizontal faces numbered first and then vertical faces.

getCellVolumes()

getExteriorFaces()

Return only the faces that have one neighboring cell.

getFaceCellIDs()

getFaceCenters()

getInteriorFaces()

Return only the faces that have two neighboring cells.

getVertexCoords()

The uniformGrid3D Module

class fipy.meshes.numMesh.uniformGrid3D.UniformGrid3D(dx=1.0, dy=1.0, dz=1.0, nx=1, ny=1, nz=1, origin=[[0], [0], [0]], overlap=2, communicator=<fipy.tools.commWrapper.CommWrapper object at 0x1068ad790>)

Bases: fipy.meshes.numMesh.grid3D.Grid3D

3D rectangular-prism Mesh with uniform grid spacing in each dimension.

X axis runs from left to right. Y axis runs from bottom to top. Z axis runs from front to back.

Numbering System:

Vertices: Numbered in the usual way. X coordinate changes most quickly, then Y, then Z.

* arrays are arranged Z, Y, X because in numerix, the final index is the one that changes the most quickly *

Cells: Same numbering system as vertices.

Faces: XY faces numbered first, then XZ faces, then YZ faces. Within each subcategory, it is numbered in the usual way.

getCellVolumes()

getExteriorFaces()

Return only the faces that have one neighboring cell.

getFaceCellIDs()

getFaceCenters()

getInteriorFaces()

Return only the faces that have two neighboring cells

getVertexCoords()