- ...distributivity.
- The
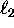inner product is commonly written as the ``dot'' product:
.
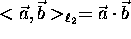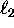We use the `dot'-notation exclusively for for inner products on vectors
and (described below) use the `dot'-notation for the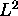 
inner product on
functions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...density
- This
relation between
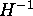and 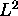is implicit in the variational
method employed in [3].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...zero
-
The integral over the boundary
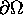usually vanishes identically, either because admissible
flows v vanish on 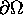(Dirichlet conditions), or
because the function which is projected onto the boundary (which depends on derivatives of f with
respect to its gradient and higher order-derivatives) in the boundary integral vanishes (Neumann
conditions).
If neither condition holds, then the boundary term must also be included in the
variation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...equation
-
These equations, including the Allen-Cahn equation below,
is sometimes written with
-terms multiplying both the gradient term
and the homogeneous part:
.
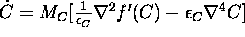This form has some advantages for the investigation of asymptotic behavior of of small .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.