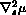
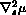
In surface diffusion, mass flux is confined to
the surface and is
is driven by gradients in chemical potential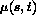 
that vary
with position 
along a surface.
In this section, we discuss the case where a facet moves without
the creation of any new facets; conditions for stepping are discussed in
section 3.
The surface recedes at places where there is a positive divergence of
flux (a negative accumulation)
and advances where the divergence is negative. Volume
(area in two-dimensions) inside a surface is conserved.
When a facet remains flat,
the velocity at any given time 
must be constant along it:
Here,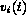 
has been scaled by a constant, 
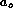, related to the
atomic size of the
diffusing species in the solid; the actual velocity is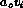 
.
Here is the position along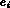 
: 
.
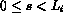All gradients are restricted to the interface-in this case they
derivatives with respect to arc length.
The flux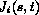 
along 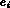is given by Ficks first law:
where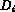 
is the
surface diffusion coefficient for the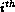 
facet.
When a facet moves a distance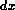 
the free energy change is
associated
with addition of new length at the two ends:
the change of surface energy of the polygon is
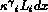, where is 
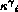is the weighted curvature
(weighted mean curvature in 3D).
In all such problems there is an arbitrary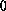 
for 
,
which we will take as the chemical potential of a crystal with
infinitely large facets. With this choice for the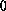
for , the energy change of incorporating the atoms into the solid
is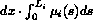 
. For equilibrium with respect
to
facet motion,
Thus the average chemical potential equals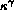 
on :
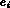Equations 4, 3 and 6 together are the crystalline formulation of motion by the Laplacian of mean curvature when the surfaces are isotropic.
Integration of Equations 4 and 3 give
that for each facet the
chemical potential is parabolic in :
where the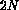 
integration constants 
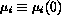and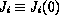 
are the chemical potential and flux at the corner,
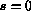of each facet, and the 
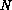values of 
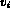are to be
determined.
Since the surface is closed,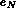 
is 
;
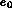hence
Continuity of chemical potential and flux at the corners gives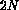
equations
Furthermore, Equation 10 and 8 imply that
so, the enclosed area is conserved as it should be for surface diffusion. Equations 8, 9, and 10, and imply:
Equations 6 and 7 give 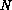more equations:
Equations 9, 10, and 13
form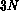 
equations in 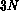unknowns and completely
determine the
flow,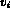 
, for each closed surface in terms of all the 
.
The lengths,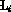 
, of the facets can be transformed into distances, 
,
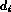from a fixed origin with:
in which each term is + if the corner is regular, and 
if not. From
this
follows a system of ordinary differential
equations for the lengths in terms of the velocities:
