


Next: 2D Formulation
Up: Shape Evolution by Surface Diffusion and Surface Attachment Limited Kinetics on Completely Faceted Surfaces
Previous: Shape Evolution by Surface Diffusion and Surface Attachment Limited Kinetics on Completely Faceted Surfaces
Modeling interface growth and shape changes
is fundamental to the study of microstructural evolution, but
tracking of the evolution of an interface
during diffusive transport is a notoriously
difficult problem, especially for anisotropic surface energies.
Use of the crystalline formulation, in which the interfaces are
assumed to be completely faceted, can avoid many of these
difficulties. In this paper, we apply this crystalline formulation to
the special cases of sintering, coarsening, and shape
equilibration where the only driving force comes from the reduction of the
energy associated with surfaces and where volume is conserved.
No other thermodynamic driving forces, such as
those which accompany phase changes, are assumed
present here, and flows which do not conserve volume, such as
motion by mean curvature (e.g. grain growth) are treated elsewhere.
(See [1] for a review.)
Volume conserving surface motion typically arises with heterophase surfaces
in
which long range diffusion of a conserved
quantity is required for motion. We will assume that surface velocities are
entirely determined by surface processes; either the diffusion is confined to
be along the surface (SD) or with more general diffusion in a surrounding
transport medium that the motion is limited by surface attachment limited
kinetics (SALK). To have volume conservation we have to assume no change in
the amount of matter stored in the transport medium. With these
restrictions we
obtain geometric laws for surface motion, which allow us to apply
recently developed methods for calculating the time evolution of shapes.
Part
of these developments is the realization that although these laws become very
difficult with mild surface energy anisotropies, they become simpler if the
anisotropy in
surface energy is so extreme that all microstructures are composed of plane
segments of a finite number of low energy orientations, for some problems
even
simpler than the isotropic cases. We therefore explore in this paper this
extreme case of anisotropy. Last we restrict ourselves to evolution of
shapes
on the plane, two-dimensional polygonal ``particles.''
The surface energy function, 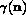 , which underlies the
driving force, is the work at constant pressure and temperature
which
must be supplied to create a unit area (length in two-dimensions) of surface
with orientation
, which underlies the
driving force, is the work at constant pressure and temperature
which
must be supplied to create a unit area (length in two-dimensions) of surface
with orientation  .
It is useful to represent
.
It is useful to represent 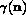 by the shape with the lowest
surface energy for a fixed volume, the
Wulff shape
by the shape with the lowest
surface energy for a fixed volume, the
Wulff shape
 .
For the special case that
.
For the special case that 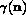 is a constant,
is a constant,
 is a sphere (circle in two dimensions).
When
is a sphere (circle in two dimensions).
When 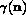 is not constant, the shape
is not constant, the shape  differs from a sphere
and in extreme cases becomes polyhedral.
For a general
differs from a sphere
and in extreme cases becomes polyhedral.
For a general 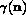 in any dimension,
in any dimension,  is given by the Wulff
construction:
is given by the Wulff
construction:
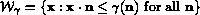 .
Note that in this construction the length scales of
.
Note that in this construction the length scales of  have units of
have units of  . The distance that a facet is from the origin of
. The distance that a facet is from the origin of  is
is 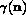 for that
for that  , but the length
, but the length 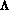 of that facet
in
of that facet
in  depends not only on the
depends not only on the  of that facet but also those of the
two adjacent facets. The Wulff construction can be easily inverted to
recover
of that facet but also those of the
two adjacent facets. The Wulff construction can be easily inverted to
recover
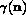 for those
for those  that appear in
that appear in  . If
. If  has missing orientations, the
values of
has missing orientations, the
values of  for those
for those  not in
not in  cannot in general be recovered, but usually do not appear in
physical problems.
cannot in general be recovered, but usually do not appear in
physical problems.
Recently developed
methods [3][2]
have shown that computations of surface evolution can often be
greatly simplified when  is ``crystalline'', that is
completely
faceted (composed of only flat surfaces and their
intersections).
In this case, the underlying surface
energy density
is ``crystalline'', that is
completely
faceted (composed of only flat surfaces and their
intersections).
In this case, the underlying surface
energy density 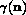 can be given as a list of
magnitudes for all orientations n which are the normal
of a facet in
can be given as a list of
magnitudes for all orientations n which are the normal
of a facet in  .
Any orientations not in
.
Any orientations not in  will break
up into facets that do appear in
will break
up into facets that do appear in  while preserving
the average orientation of the surface.
while preserving
the average orientation of the surface.
We are interested in motions which decrease surface energy. The limit of
change
in surface energy with volume under small deformations is by definition the
weighted mean curvature (or weighted
curvature in two dimensions), 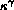 [4].
[4]. ``Small" usually means local, but in the case of facets should
mean motion of an entire facet by a small distance.
``Small" usually means local, but in the case of facets should
mean motion of an entire facet by a small distance.
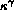 is thus defined on a facet-by-facet basis by considering energy
changes involved in moving the entire facet keeping its normal direction fixed. While
the chemical
potential may vary along a facet,
the average chemical potential across the facet equals
is thus defined on a facet-by-facet basis by considering energy
changes involved in moving the entire facet keeping its normal direction fixed. While
the chemical
potential may vary along a facet,
the average chemical potential across the facet equals 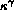 on that
facet.
For polygonal
on that
facet.
For polygonal  ,
,
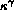 has a particularly
simple form, based on
has a particularly
simple form, based on  , given in Section 2.
, given in Section 2.
The methods developed for anisotropic problems can be
useful for approximating isotropic problems. Motion by crystalline
curvature, where the normal velocity of each facet
 is proportional to its crystalline curvature and volume is not conserved,
has been proven to converge to motion by (isotropic)
curvature for two dimensional problems, as
is proportional to its crystalline curvature and volume is not conserved,
has been proven to converge to motion by (isotropic)
curvature for two dimensional problems, as  approaches a circle
(though a sequence of regular polygons with the
number of sides becoming infinite)
[7][6][5].
It remains to be shown whether other types of motion will likewise converge
to the isotropic case. In the case of surface diffusion, there does
not now exist a good way of computing isotropic surface diffusion, so
its approximation by this crystalline method is currently the best way
of computing it, assuming that these approximations do in fact
converge to it.
approaches a circle
(though a sequence of regular polygons with the
number of sides becoming infinite)
[7][6][5].
It remains to be shown whether other types of motion will likewise converge
to the isotropic case. In the case of surface diffusion, there does
not now exist a good way of computing isotropic surface diffusion, so
its approximation by this crystalline method is currently the best way
of computing it, assuming that these approximations do in fact
converge to it.



Next: 2D Formulation
Up: Shape Evolution by Surface Diffusion and Surface Attachment Limited Kinetics on Completely Faceted Surfaces
Previous: Shape Evolution by Surface Diffusion and Surface Attachment Limited Kinetics on Completely Faceted Surfaces
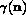 , which underlies the
driving force, is the work at constant pressure and temperature
which
must be supplied to create a unit area (length in two-dimensions) of surface
with orientation
, which underlies the
driving force, is the work at constant pressure and temperature
which
must be supplied to create a unit area (length in two-dimensions) of surface
with orientation  .
It is useful to represent
.
It is useful to represent 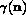 by the shape with the lowest
surface energy for a fixed volume, the
Wulff shape
by the shape with the lowest
surface energy for a fixed volume, the
Wulff shape
 .
For the special case that
.
For the special case that 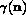 is a constant,
is a constant,
 is a sphere (circle in two dimensions).
When
is a sphere (circle in two dimensions).
When 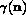 is not constant, the shape
is not constant, the shape  differs from a sphere
and in extreme cases becomes polyhedral.
For a general
differs from a sphere
and in extreme cases becomes polyhedral.
For a general 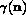 in any dimension,
in any dimension,  is given by the Wulff
construction:
is given by the Wulff
construction:
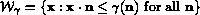 .
Note that in this construction the length scales of
.
Note that in this construction the length scales of  have units of
have units of  . The distance that a facet is from the origin of
. The distance that a facet is from the origin of  is
is 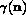 for that
for that  , but the length
, but the length 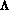 of that facet
in
of that facet
in  depends not only on the
depends not only on the  of that facet but also those of the
two adjacent facets. The Wulff construction can be easily inverted to
recover
of that facet but also those of the
two adjacent facets. The Wulff construction can be easily inverted to
recover
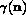 for those
for those  that appear in
that appear in  . If
. If  has missing orientations, the
values of
has missing orientations, the
values of  for those
for those  not in
not in  cannot in general be recovered, but usually do not appear in
physical problems.
cannot in general be recovered, but usually do not appear in
physical problems.
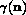 can be given as a list of
magnitudes for all orientations n which are the normal
of a facet in
can be given as a list of
magnitudes for all orientations n which are the normal
of a facet in 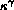
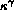 is thus defined on a facet-by-facet basis by considering energy
changes involved in moving the entire facet keeping its normal direction fixed. While
the chemical
potential may vary along a facet,
the average chemical potential across the facet equals
is thus defined on a facet-by-facet basis by considering energy
changes involved in moving the entire facet keeping its normal direction fixed. While
the chemical
potential may vary along a facet,
the average chemical potential across the facet equals  is proportional to its crystalline curvature and volume is not conserved,
has been proven to converge to motion by (isotropic)
curvature for two dimensional problems, as
is proportional to its crystalline curvature and volume is not conserved,
has been proven to converge to motion by (isotropic)
curvature for two dimensional problems, as