Abstract
We consider traveling wave solutions of
reaction-diffusion equations with nonlocal variable diffusion and
bistable nonlinearities.
For the case of spatially periodic
diffusion we obtain analytic solutions for the
traveling wave problem using a
piecewise linear nonlinearity.
The formula for the
wave forms is implicitly defined in the
general periodic case and we provide an explicit formula
for the case of period two diffusion.
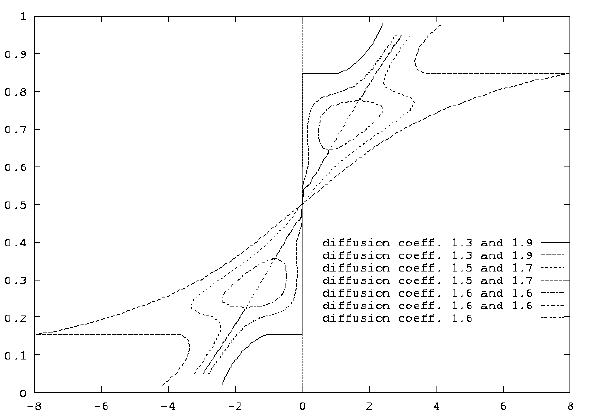
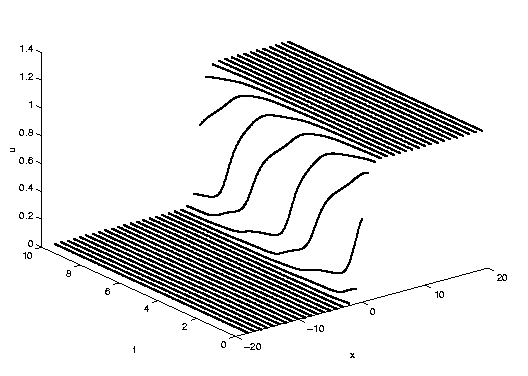
We present numerical results for the the cases
of homogeneous, period two,
and period four diffusion coefficients using a
cubic nonlinearity,
and uncover, numerically, a period doubling bifurcation
in the wave speed versus detuning parameter relation.
back


