In this model, we depend on the assumption that the travelling wave is
fully developed, so that
the dissolving grain, occupying the region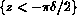 
, has a
given
limiting
concentration 
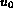as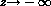 
, and the grain being formed in the
wake of
the moving interface has
a limiting concentration profile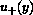 
as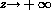 
, which is
unknown at
the moment.
At any location, the equilibrium lattice spacing of a
perfect crystal is generally determined by the solute concentration 
, and
therefore a
spatial
variation of in either grain will induce stress, whose energy should be
incorporated into the free energy functional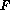 
.
In the dissolving grain, the stress energy density in our
approximation will
take the form
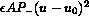, with 
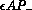positive. In the
advancing grain, which we suppose to be
disconnected as explained below from the other grain, it is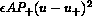 
.
In the interface where any crystalline structure is imperfect, the
transmission of stress due to concentration differences is weakened. This
fact is the source of a coupling between the two fields and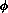 
, and
hence of a stress-induced term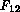 
.
We model the ability to transmit stress in this way as an all-or-none
phenomenon. No stress can be transmitted to
neighboring
portions of the metal across a sufficiently disordered layer, say when
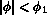for some 
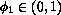, but stresses
due to nonconstant in the dissolving (advancing) grain occur as
though it
were a perfect crystal occupying the entire region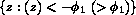 
.
Since there will be no stress energy in the region
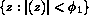, the scaled coupling free energy
density
(see (6)) can be written
where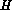 
is the Heaviside function (unit step function).
Expressing the derivative of 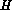as a delta-function, we obtain
where the bars indicate averages over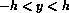 
at fixed 
.
After some tedious calculations using (20), (27), and
(30), we find under certain assumptions on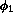 
and the other
parameters that
Other expressions are obtained from different assumptions, but in all
cases,
is an even function of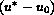 
, so that a reversal of the sign of
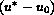has no effect on the velocity. This appears to conform to some
experiments, but more investigation is needed. We conclude that this
effect
is a feasible impetus for the motion.
A possibly more realistic case is that in which both effects in this
and the
last
section
occur, with different values of 
. Then an expression for
depending
on these two values can easily be obtained.