It was suggested by Meyrick [6] that interface motion in some contexts could be caused by an interaction in which the interfacial free energy depends on the concentration of solute atoms. This interaction is analogous to the Marangoni effect [7][5], in which an interface moves because the surface tension of a fluid depends on concentration or temperature.
In our context, the interfacial free energy should be interpreted as
the term
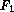in (1). A simple way to model this mechanism is to make
the
coefficient
of 
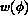in the formula (2) depend linearly on
. This is equivalent to
adding a term of the form (6) in which
so that, by (3),
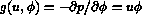for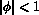 
.
The coefficient 
in (6)
can be of either sign. If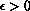 
,
the interaction free energy density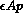 
increases with at fixed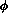 
, and so it is expected that the
interface
will tend to move towards smaller values of . If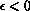 
,
it would tend to move the other way.
With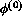 
given by (20) and 
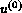by (27),
formula (30) now yields
Our setup requires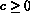 
. For the Meyrick mechanism,
the boundary can therefore move only if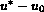 
has the same sign
as
. Even if the signs are right, there is no guarantee that
(32) can be solved for 
. The right side also depends on
through 
(26), resulting in an implicit equation for . If a
solution with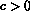 
exits, one factor ``'' may be eliminated from both
sides. The equation for so obtained has a solution only if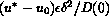 
is large enough.
However, experiments [3] have shown
that for many alloy systems, it is possible for the grain boundary to
move
for either sign of
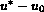(The direction of motion of the boundary depends on
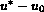the sign of ). So a term of the form
(31) cannot provide the sole driving force for DIGM.