


Next: Travelling wave solutions
Up: No Title
Previous: Introduction

We use a diffuse-interface model with an order parameter 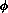 and a
concentration
and a
concentration  as the only field variables. Moreover, the
interface we
consider is straight and represents a boundary between two grains of
the same
phase. In particular, we exclude at the outset any influence that
curvature of the
boundary or temperature variation may have on the motion. In reality,
these
boundaries
are usually curved; that additional effect has just not as yet been
included in our model.
as the only field variables. Moreover, the
interface we
consider is straight and represents a boundary between two grains of
the same
phase. In particular, we exclude at the outset any influence that
curvature of the
boundary or temperature variation may have on the motion. In reality,
these
boundaries
are usually curved; that additional effect has just not as yet been
included in our model.
Typically, the
concentration  could represent the fraction of available lattice
sites
which are filled by solute atoms, and so we shall take its range to be
the
interval
could represent the fraction of available lattice
sites
which are filled by solute atoms, and so we shall take its range to be
the
interval 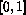 . Similarly
. Similarly 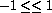 , the two extremes
, the two extremes 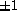 representing the two perfect grains on either side.
representing the two perfect grains on either side.
As is usual with diffuse-interface models (e.g. [2]), the
postulated evolution system can be understood
as a gradient flow with respect to a functional. In this case, the
functional is
appropriately named the free energy 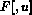 , since temperature will
be
constant. It has contributions coming individually from
, since temperature will
be
constant. It has contributions coming individually from 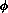 and
and
 , plus a small contribution resulting from the interaction between
the two
fields:
, plus a small contribution resulting from the interaction between
the two
fields:

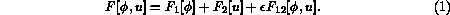
The first term will be of standard van der Waals-Cahn-Hilliard form

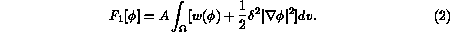
Here 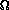 is the domain in space occupied by the solid material.
Rather,
assuming everything is independent of one space coordinate, we take
it to be
the strip
is the domain in space occupied by the solid material.
Rather,
assuming everything is independent of one space coordinate, we take
it to be
the strip 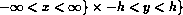 , representing a 2D
cross
section of the metal film. The grain boundary will be a subregion of
, representing a 2D
cross
section of the metal film. The grain boundary will be a subregion of
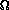 consisting of a slim rectangle
consisting of a slim rectangle 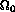 bounded on top and bottom by the
two
faces
bounded on top and bottom by the
two
faces 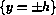 . The law of motion of this rectangle is our
primary
object of interest. The parameter
. The law of motion of this rectangle is our
primary
object of interest. The parameter 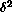 is some measure of the
relative
weight attached to gradients of
is some measure of the
relative
weight attached to gradients of 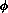 in the expression for the free
energy
(we shall see that
in the expression for the free
energy
(we shall see that 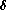 is also a measure of the
thickness of the interface
is also a measure of the
thickness of the interface 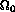 ), and
), and 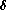 is approximately the free
energy
density if
is approximately the free
energy
density if 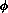 were constant in space. We take it to be the
following
double-well potential with barrier at
were constant in space. We take it to be the
following
double-well potential with barrier at 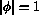 (see, e.g.
[1]):
(see, e.g.
[1]):

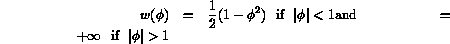
For the values 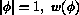 is left undefined.
is left undefined.
We take

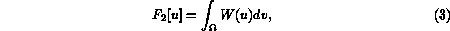
where 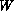 is a convex function representing the free energy density of
the
solid due to the presence of the solute. A typical form for
is a convex function representing the free energy density of
the
solid due to the presence of the solute. A typical form for 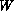 is
is

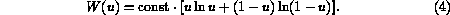
Other effects of the type we are seeking can be obtained by including
terms
involving 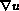 in (4); we shall omit them for simplicity.
in (4); we shall omit them for simplicity.
Our object will be to discover interaction terms 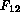 which can
serve as
impetus for the motion of the interface and which have physical
interpretations. They will be of the assumed form
which can
serve as
impetus for the motion of the interface and which have physical
interpretations. They will be of the assumed form

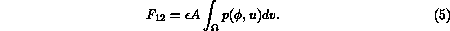
The small dimensionless normalizing parameter  is
chosen so that the derivatives of
is
chosen so that the derivatives of  are of order unity. Setting
are of order unity. Setting
 ,
we assume the smallness relations
,
we assume the smallness relations

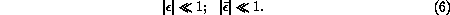
Our chosen kinetic equations take the form

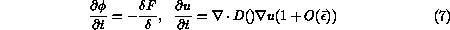
(the error term depends on  and will not be given explicitly),
where
and will not be given explicitly),
where
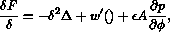
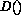 represents the diffusivity of the solute as a function of the
degree (measured by
represents the diffusivity of the solute as a function of the
degree (measured by 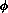 ) to which the material is ordered, and
) to which the material is ordered, and  is a
relaxation time.
is a
relaxation time.
One interpretation and/or derivation of the system (8) involves
its
characterization as a gradient (steepest descent)
flow for the functional 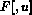 with respect to a certain
with respect to a certain
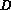 -dependent
scalar product, at least in the case that
-dependent
scalar product, at least in the case that 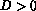 and
and 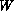 is given by
(5).
is given by
(5).
We are mostly interested, however, in the case when 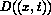 vanishes in much of the domain of interest; the gradient nature of the
flow
then degenerates.
It is well known, in fact, that the diffusivity is
much larger in the grain boundary than in a perfect crystal.
We shall make the simplifying assumption that
vanishes in much of the domain of interest; the gradient nature of the
flow
then degenerates.
It is well known, in fact, that the diffusivity is
much larger in the grain boundary than in a perfect crystal.
We shall make the simplifying assumption that
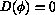 in the crystals, that is when
in the crystals, that is when 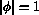 .
Our specific choice for
.
Our specific choice for 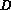 is
is

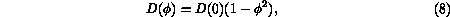
where 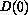 is a constant.
is a constant.
By the choice (3) of 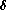 , the system (8) now becomes
, the system (8) now becomes

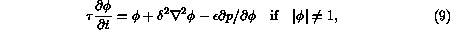

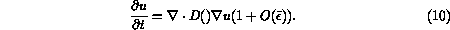
To account for the possibility that 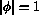 , we extend
(10) as
a variational inequality (see [1] for an analogous
situation).
The
result is that in places where
, we extend
(10) as
a variational inequality (see [1] for an analogous
situation).
The
result is that in places where 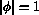 , (10) need not hold;
all that is necessary there is for
, (10) need not hold;
all that is necessary there is for 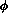 and its gradient
to be continuous.
and its gradient
to be continuous.
As boundary conditions on 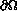 , physical considerations suggest that
, physical considerations suggest that

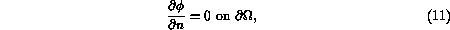
where 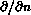 denotes differentiation in the
direction normal to
denotes differentiation in the
direction normal to 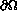 , and (neglecting
, and (neglecting  )
)

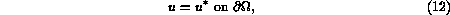
where 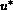 is a given value depending on the properties of the
external
vapor.
is a given value depending on the properties of the
external
vapor.
Conditions at 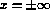 are also needed. We require
are also needed. We require

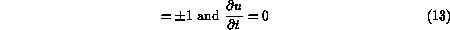
in regions to the left and right in our strip domain 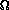 where
the pure
crystals reside, i.e. where
where
the pure
crystals reside, i.e. where 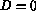 . These regions are not known at
the outset.
. These regions are not known at
the outset.



Next: Travelling wave solutions
Up: No Title
Previous: Introduction
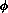 and a
concentration
and a
concentration  as the only field variables. Moreover, the
interface we
consider is straight and represents a boundary between two grains of
the same
phase. In particular, we exclude at the outset any influence that
curvature of the
boundary or temperature variation may have on the motion. In reality,
these
boundaries
are usually curved; that additional effect has just not as yet been
included in our model.
as the only field variables. Moreover, the
interface we
consider is straight and represents a boundary between two grains of
the same
phase. In particular, we exclude at the outset any influence that
curvature of the
boundary or temperature variation may have on the motion. In reality,
these
boundaries
are usually curved; that additional effect has just not as yet been
included in our model.
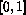 . Similarly
. Similarly 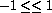 , the two extremes
, the two extremes 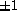 representing the two perfect grains on either side.
representing the two perfect grains on either side.
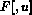 , since temperature will
be
constant. It has contributions coming individually from
, since temperature will
be
constant. It has contributions coming individually from 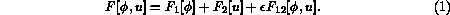
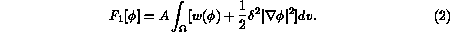
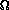 is the domain in space occupied by the solid material.
Rather,
assuming everything is independent of one space coordinate, we take
it to be
the strip
is the domain in space occupied by the solid material.
Rather,
assuming everything is independent of one space coordinate, we take
it to be
the strip 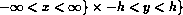 , representing a 2D
cross
section of the metal film. The grain boundary will be a subregion of
, representing a 2D
cross
section of the metal film. The grain boundary will be a subregion of
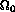 bounded on top and bottom by the
two
faces
bounded on top and bottom by the
two
faces 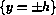 . The law of motion of this rectangle is our
primary
object of interest. The parameter
. The law of motion of this rectangle is our
primary
object of interest. The parameter 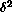 is some measure of the
relative
weight attached to gradients of
is some measure of the
relative
weight attached to gradients of 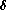 is also a measure of the
thickness of the interface
is also a measure of the
thickness of the interface 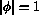 (see, e.g.
(see, e.g.
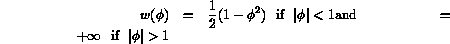
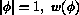 is left undefined.
is left undefined.
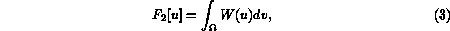
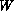 is a convex function representing the free energy density of
the
solid due to the presence of the solute. A typical form for
is a convex function representing the free energy density of
the
solid due to the presence of the solute. A typical form for 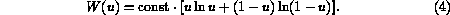
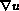 in (
in (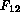 which can
serve as
impetus for the motion of the interface and which have physical
interpretations. They will be of the assumed form
which can
serve as
impetus for the motion of the interface and which have physical
interpretations. They will be of the assumed form
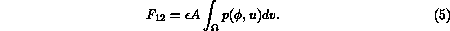
 is
chosen so that the derivatives of
is
chosen so that the derivatives of  are of order unity. Setting
are of order unity. Setting
 ,
we assume the smallness relations
,
we assume the smallness relations
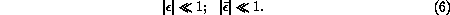
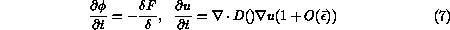
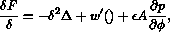
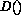 represents the diffusivity of the solute as a function of the
degree (measured by
represents the diffusivity of the solute as a function of the
degree (measured by  is a
relaxation time.
is a
relaxation time.
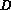 -dependent
scalar product, at least in the case that
-dependent
scalar product, at least in the case that 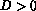 and
and 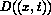 vanishes in much of the domain of interest; the gradient nature of the
flow
then degenerates.
It is well known, in fact, that the diffusivity is
much larger in the grain boundary than in a perfect crystal.
We shall make the simplifying assumption that
vanishes in much of the domain of interest; the gradient nature of the
flow
then degenerates.
It is well known, in fact, that the diffusivity is
much larger in the grain boundary than in a perfect crystal.
We shall make the simplifying assumption that
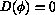 in the crystals, that is when
in the crystals, that is when 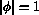 .
Our specific choice for
.
Our specific choice for 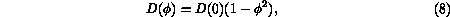
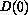 is a constant.
is a constant.
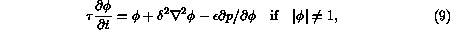
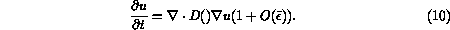
 and its gradient
to be continuous.
and its gradient
to be continuous.
 , physical considerations suggest that
, physical considerations suggest that
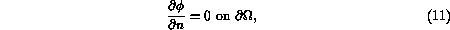
 denotes differentiation in the
direction normal to
denotes differentiation in the
direction normal to  , and (neglecting
, and (neglecting  )
)
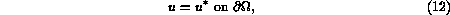
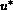 is a given value depending on the properties of the
external
vapor.
is a given value depending on the properties of the
external
vapor.
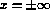 are also needed. We require
are also needed. We require
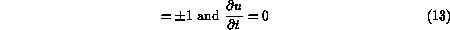
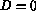 . These regions are not known at
the outset.
. These regions are not known at
the outset.