Interfaces separating crystalline grains in polycrystalline solids, such as
metal and ceramics, are sometimes observed to
migrate, causing some grains to grow at the expense of others. When this is
motion by curvature, it is called grain growth. But in the presence of
chemical composition gradients, there is another cause for the motion that
has
been found to be strong enough to overwhelm motion by curvature,
when curvatures are less than approximately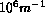 
.
This
phenomenon, called diffusion-induced grain boundary motion (DIGM),
was first discovered by Hillert and Purdy in 1977 [4]. A particularly
simple geometry for observing this phenomenon is a
thin metallic film containing transverse planar grain boundaries, immersed in a
vapor containing a
substance that
can be incorporated in the crystals as a solute in a solid solution.
Although
DIGM has been studied extensively
and various explanations have been
proposed, the true mechanism underlying this type of boundary migration
remains something of a mystery.
It is the purpose of this note to report on progress made on a theoretical basis for the observed coupling of the motion of such a grain boundary with the solute diffusion field within the boundary itself. We consider a phase-field model for an abstract diffuse interface that has many of the attributes of a grain boundary. We take the boundary to be a thin mobile zone of disorder (grain boundary) in which the solute diffuses rapidly, between two highly ordered regions (crystalline grains) with low diffusivities. The ordered regions support stress, but this stress is not transmitted through the zone where the ordering is low. Since grain boundaries are surfaces between grains of the same phase, differing only in the orientation of the crystal axes, the properties of both crystalline grains are represented by only the solute concentration and the magnitude of an order parameter.
Two coupling mechanisms are considered within the context of our phase field model: the dependence of the stress in the ordered grains on the concentration of the diffusing element (Sec. 6) and the dependence of the interfacial free energy on this same concentration (Sec. 5). Both effects are found to produce boundary motion under certain conditions, and the velocity is estimated in terms of the other parameters and data entering the model, such as the diffusivity, the initial concentration in the crystal, and that in the surrounding vapor.