μMAG Standard Problem #5
Adapted from proposed problem published by Najafi, et al.
[1].
Please send comments to
donald.porter@nist.gov
and join the μMAG
discussion e-mail
list for ongoing discussion.
Specification
This problem serves as a test of proper basic functioning of
those micromagnetic solvers that include the effects of spin
momentum transfer between in-plane polarized current and spatial patterns
of magnetism. The movement of a magnetic vortex in response to
a constant current flowing in the plane of magnetic material
is computed. The final vortex position and its trajectory serve
as results to be compared among different solvers. The problem
is to be solved for a sequence of values for the degree of
non-adiabaticity to detect any divergence of results among solvers
over the range.
Geometry
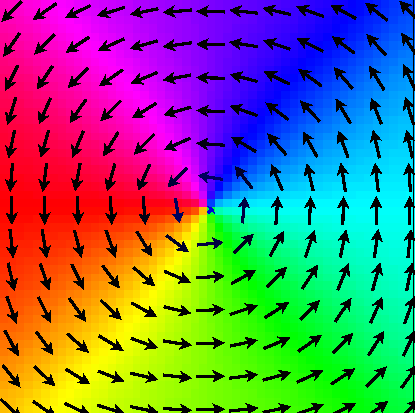
A rectangular film of magnetic material with dimensions
100 nm × 100 nm × 10 nm, aligned with the
x,
y,
z
axes of a Cartesian coordinate system, with origin
at the center of the film.
Material Parameters
Similar to Permalloy:
Saturation magnetization:
Ms
=
8.0e5
A/m
Exchange constant:
A
=
1.3e-11
J/m
Anisotropy energy density:
K
=
0
J/m3
Gilbert damping parameter:
α
=
0.1
Gilbert gyromagnetic ratio:
γ0
=
2.211e5
m/C
[ = (rad/s)/(A/m)]
With these values, the exchange length is 5.7 nm.
Initial State
At each point
xyz
within the magnetic
material, set the initial magnetization direction so that
m
=
M
/
M
s
=
f
/
f
where
f
x
,
y
,
z
=
-y
,
x
,
R
T
and
R=
10
nm.
From that initial state, solve
the Landau-Lifshitz-Gilbert dynamics
d
m
d
t
=
-
γ
0
m
×
H
+
α
m
×
d
m
d
t
to reach an equilibrium configuration. This magnetization vortex
pattern is the initial state for all the remaining simulations.
Applied Current
To the initial magnetization vortex pattern, an in-plane current is applied
in the
x
direction, with the product of the polarization
rate
P
and current density
J
given by
P
J
=
10
12
x
^
in units of A/m2, where
x
^
is the unit vector in the positive
x
direction.
Boundary Conditions
Outside of the magnetic material, the applied current is unpolarized.
This places conditions on the boundaries where current enters and leaves
the magnetic material. At those surfaces care must be taken with the
calculation such that the applied current delivers zero spin
torque to the magnetization there.
Spin Torque Dynamics
Equation (3) of Thiaville, et al. [2] describes
the magnetization
dynamics including spin torque with an extended LLG equation.
|
d
m
d
t
=
γ
0
H
×
m
+
α
m
×
d
m
d
t
-
u
T
⋅∇
m
+
β
m
×
u
T
⋅∇
m
|
(1)
|
where the new terms introduce a velocity vector (in m/s)
|
u
T
=
-
P
g
μ
B
J
2
e
M
s
|
(2)
|
and a dimensionless quantity
β
representing the degree of non-adiabaticity.
In the definition of the velocity vector,
we take
g
to be 2 and we have the physical constants
Bohr magneton:
μB
=
9.274e-24
J/T
Elementary charge:
e
=
1.6022e-19
C
Given these constants and the material parameters already specified,
the magnitude and direction of
u
T
is determined
by the applied current alone, independent of the value of
β.
For this problem we have
u
T
=
-
72.35
x
^
in units of m/s.
Equation (1) of Najafi, et al. [1] describes
the magnetization dynamics with a different extended LLG equation
adapted from Equation (11) of Zhang and Li [3],
|
d
M
d
t
=
-
γ
0
M
×
H
+
α
M
s
M
×
d
M
d
t
-
b
M
s
2
M
×
M
×
J
⋅∇
M
-
ξ
b
M
s
M
×
J
⋅∇
M.
|
(3)
|
Here the new terms also introduce a dimensionless
quantity
ξ
representing the degree of non-adiabaticity,
as well as a factor
|
b
=
P
μ
B
e
M
s
1
+
ξ
2
|
(4)
|
with units of m3/C.
The functional dependence of
b
on
ξ
observed in (4)
but not in (2) makes clear that equations (1) and (3) above do not
predict the same variation of dynamics over a range of inputs
describing different physical scenarios. They are equivalent for
only the specific case of
ξ=0
(and because of our assumption that
g=2
). As the degree of non-adiabaticity
is varied, the two models diverge in their calculations.
Equations (1) and (3) may be reconciled into a common form
|
d
m
d
t
=
-
γ
0
m
×
H
+
α
m
×
d
m
d
t
-
u
m
×
∂
m
∂
x
×
m
+
ξ
u
m
×
∂
m
∂
x
|
(5)
|
where we have also simplified the expression using knowledge
of the direction of the applied current.
The same equation can be expressed in explicit Landau-Lifshitz form as
|
1
+
α
2
d
m
d
t
=
-
γ
0
m
×
H
+
α
γ
0
m
×
H
×
m
-
u
1
+
α
ξ
m
×
∂
m
∂
x
×
m
+
u
ξ
-
α
m
×
∂
m
∂
x
.
|
(6)
|
In order to contribute
a solution to this standard problem, a solver needs to be able to compute
solutions of (5) [equivalently (6)] for at least some values of
u
and
ξ
under control of user inputs.
Problem Sets
The originally published standard problem from [1]
explicitly demands that equation (3) be solved, and it sets the
value of
ξ
=0.05.
Translated into the common form, we seek
solutions of (5) for
ξ
=0.05
and
u
=
-
b
J
=
u
T
1
+
ξ
2
=
-
72.17
m/s.
If your solver permits direct entry of the quantities
u
and
ξ,
this is a simple matter. If not, it is necessary to
determine what values of what available inputs are needed to produce
the same results. For a solver that has the assumptions of equation (1)
deeply embedded in it, this may involve entry of a value of applied
current scaled by the factor
(
1+
ξ
2
)
.
Then, to explore and verify solver operations over other values of
ξ,
we ask that the solutions of (3) be computed for
ξ
set to the values 0, 0.1 (=
α),
and 0.5. This
corresponds to solutions of (5) for
u
set to the values
-72.35 m/s, -71.64 m/s, and -57.88 m/s. The aim is to cover interesting
example cases to verify proper solver functioning.
Submitters are also invited to submit whatever solutions
their solver deems to be an appropriate solution for the physical
parameters specified without any attempt to force a solution of (3)
from your software if it prefers something else, also for the range
of values for
ξ
set to 0, 0.05, 0.1 (=
α),
and 0.5.
When
ξ=0,
equations (1) and (3) compute
precisely the same dynamics. This is an
important baseline case. Divergent solutions here indicate likely
program errors.
When
ξ=0.05,
the computed results can be compared with
the results found in [1].
When
ξ=0.1=α,
the final term of the Landau-Lifshitz
form of the dynamics (6) vanishes. Testing this case is useful for detecting
whether that leads to any trouble with the implementation.
Finally, when
ξ=0.5,
the different solutions of (1) and (3)
are great enough to observe with certainty. There may be no material
for which this calculation is meaningful, but there is value as a
unit of software testing.
To summarize, submissions should include computed solutions of
one of the three equivalent sets of problems:
-
Solve (1) for:
u T
= - 72.35
x ^
m/s
and
β = 0
u T
= - 72.17
x ^
m/s
and
β = 0.05
u T
= - 71.64
x ^
m/s
and
β = 0.1
u T
= - 57.88
x ^
m/s
and
β = 0.5
-
Solve (3) for:
b J
= 72.35
m/s
and
ξ = 0
b J
= 72.17
m/s
and
ξ = 0.05
b J
= 71.64
m/s
and
ξ = 0.1
b J
= 57.88
m/s
and
ξ = 0.5
-
Solve (5) for:
u
= - 72.35
m/s
and
ξ = 0
u
= - 72.17
m/s
and
ξ = 0.05
u
= - 71.64
m/s
and
ξ = 0.1
u
= - 57.88
m/s
and
ξ = 0.5
In addition, submitters may submit whatever solutions they believe
more properly compute the physical problem posed with degree of
non-adiabaticity from the set
0
0.05
0.1
0.5
.
Submissions
So long as the single vortex structure of the magnetization is not
lost during the simulation, the spatially averaged components of
magnetization
Mx
and
My
are a good proxy for the vortex location, and are easy to compute.
For each completed
simulation, a text file should be submitted with three columns
of numeric values. The first column should report the simulation
time value in seconds.
The second column should report the
spatially averaged magnetization component
Mx
computed for that instant in time in A/m.
The third column should report the
spatially averaged magnetization component
My
computed for that instant in time in A/m.
Lines beginning with the # character can be used to make
comments that will not be processed as data. The time resolution of the
data should
be fine enough to represent the vortex trajectory well. A suggested
minimum time sampling for submission is one data line for every
100 ps of simulation time. The data need not be evenly sampled.
The trajectories should continue until the submitter is satisfied
an equilibrium location of the vortex has been reached. The results
in [1] suggest this means a period of about 14 ns.
For each submitted file that represents a solution of (5), the values
of
u
and
ξ
should be identified. Other submissions should
include whatever other description will make clear the problem solution
they represent.
All solution files may be gathered up into any common archive format
and transmitted to
donald.porter@nist.gov
for archiving and publication on the μMAG Standard Problem pages.
Simultaneous reporting to the μMAG mailing list is optional.
Submissions should identify the solver tested, and any other details
needed for others to replicate the results.
References
[1]
Proposal for a standard problem for micromagnetic simulations
including spin-transfer torque,
M. Najafi, B. Krüger, S. Bohlens, M. Franchin, H. Fangohr, A. Vanhaverbeke,
R. Allenspach, M. Bolte, U. Merkt, D. Pfannkuche, D.P.F. Möller, and G. Meier,
Journal of Applied Physics, 105, 113914 (8 pages) (Jun 2009).
[2]
Micromagnetic understanding of current-driven domain wall motion in
patterned nanowires,
A. Thiaville, Y. Nakatani, J. Miltat, Y. Suzuki,
Europhysics Letters, 69, 990 (7 pages) (March 2005).
[3]
Roles of nonequilibrium conduction electrons on the magnetization
dynamics of ferromagnets, S. Zhang and Z. Li,
Physical Review Letters, 93, 127204 (4 pages) (September 2004)
Please send comments to donald.porter@nist.gov and join the
µMAG discussion e-mail list.
Site Directory
µMAG organization / NIST CTCMS /
donald.porter@nist.gov
Date created: 29-Sep-2014 | Last updated: 14-May-2018
