`variables` Package Documentation¶

This page contains the variables Package documentation.

The `addOverFacesVariable` Module¶

The `arithmeticCellToFaceVariable` Module¶

The `betaNoiseVariable` Module¶

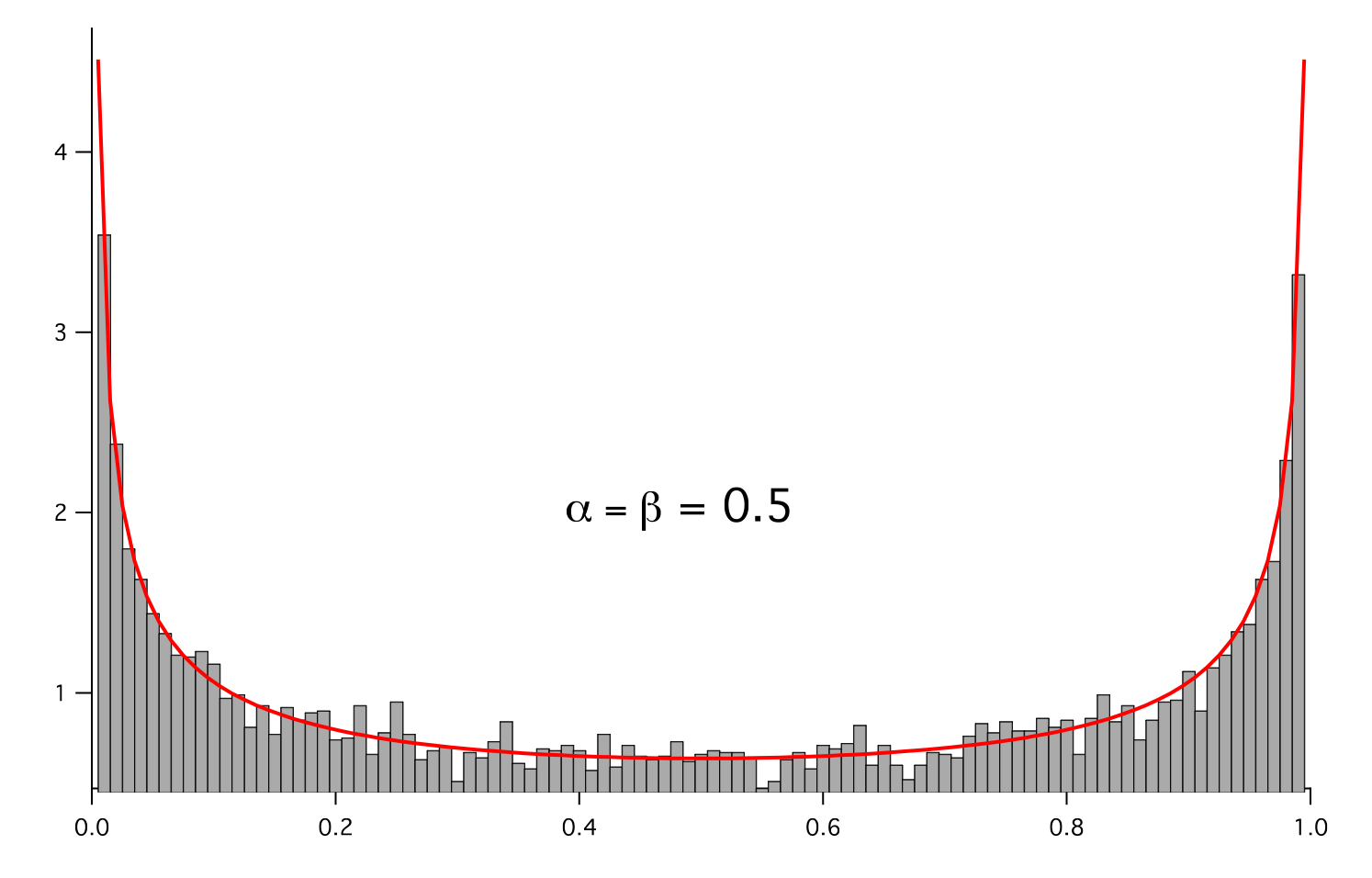
class fipy.variables.betaNoiseVariable.BetaNoiseVariable(mesh, alpha, beta, name='', hasOld=0)¶

Bases: fipy.variables.noiseVariable.NoiseVariable

Represents a beta distribution of random numbers with the probability distribution

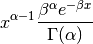
$x^{\alpha - 1}\frac{\beta^\alpha e^{-\beta x}}{\Gamma(\alpha)}$

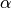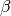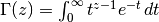with a shape parameter $\alpha$ , a rate parameter $\beta$ , and $\Gamma(z) = \int_0^\infty t^{z - 1}e^{-t}\,dt$ .

We generate noise on a uniform cartesian mesh

>>> from fipy.variables.variable import Variable
>>> alpha = Variable()
>>> beta = Variable()
>>> from fipy.meshes.grid2D import Grid2D
>>> noise = BetaNoiseVariable(mesh = Grid2D(nx = 100, ny = 100), alpha = alpha, beta = beta)

We histogram the root-volume-weighted noise distribution

>>> from fipy.variables.histogramVariable import HistogramVariable
>>> histogram = HistogramVariable(distribution = noise, dx = 0.01, nx = 100)

and compare to a Gaussian distribution

>>> from fipy.variables.cellVariable import CellVariable
>>> betadist = CellVariable(mesh = histogram.getMesh())
>>> x = histogram.getMesh().getCellCenters()[0]

>>> if __name__ == '__main__':
...     from fipy import Viewer
...     viewer = Viewer(vars=noise, datamin=0, datamax=1)
...     histoplot = Viewer(vars=(histogram, betadist), 
...                        datamin=0, datamax=1.5)

>>> from fipy.tools.numerix import arange, exp
>>> from scipy.special import gamma as Gamma

>>> for a in arange(0.5,5,0.5):
...     alpha.setValue(a)
...     for b in arange(0.5,5,0.5):
...         beta.setValue(b)
...         betadist.setValue((Gamma(alpha + beta) / (Gamma(alpha) * Gamma(beta))) 
...                           * x**(alpha - 1) * (1 - x)**(beta - 1))
...         if __name__ == '__main__':
...             import sys
...             print >>sys.stderr, "alpha: %g, beta: %g" % (alpha, beta)
...             viewer.plot()
...             histoplot.plot()

>>> print abs(noise.getFaceGrad().getDivergence().getCellVolumeAverage()) < 5e-15
1

histogram of random values with a beta distribution

Parameters :	mesh: The mesh on which to define the noise. alpha: The parameter 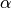$\alpha$ . beta: The parameter $\beta$ .

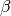random()¶

The `binaryOperatorVariable` Module¶

The `cellToFaceVariable` Module¶

The `cellVariable` Module¶

class fipy.variables.cellVariable.CellVariable(mesh, name='', value=0.0, rank=None, elementshape=None, unit=None, hasOld=0)¶

Bases: fipy.variables.meshVariable._MeshVariable

Represents the field of values of a variable on a Mesh.

A CellVariable can be pickled to persistent storage (disk) for later use:

>>> from fipy.meshes.grid2D import Grid2D
>>> mesh = Grid2D(dx = 1., dy = 1., nx = 10, ny = 10)

>>> var = CellVariable(mesh = mesh, value = 1., hasOld = 1, name = 'test')
>>> x, y = mesh.getCellCenters()
>>> var.setValue(x * y)

>>> from fipy.tools import dump        
>>> (f, filename) = dump.write(var, extension = '.gz')
>>> unPickledVar = dump.read(filename, f)

>>> print var.allclose(unPickledVar, atol = 1e-10, rtol = 1e-10)
1

copy()¶

getArithmeticFaceValue()¶

Returns a FaceVariable whose value corresponds to the arithmetic interpolation of the adjacent cells:

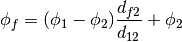
$\phi_f = (\phi_1 - \phi_2) \frac{d_{f2}}{d_{12}} + \phi_2$

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy import numerix
>>> mesh = Grid1D(dx = (1., 1.))
>>> L = 1
>>> R = 2
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getArithmeticFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = (R - L) * (0.5 / 1.) + L
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

>>> mesh = Grid1D(dx = (2., 4.))
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getArithmeticFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = (R - L) * (1.0 / 3.0) + L
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

>>> mesh = Grid1D(dx = (10., 100.))
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getArithmeticFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = (R - L) * (5.0 / 55.0) + L
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

getCellVolumeAverage()¶

Return the cell-volume-weighted average of the CellVariable:

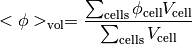
$<\phi>_\text{vol} = \frac{\sum_\text{cells} \phi_\text{cell} V_\text{cell}} {\sum_\text{cells} V_\text{cell}}$

>>> from fipy.meshes.grid2D import Grid2D
>>> from fipy.variables.cellVariable import CellVariable
>>> mesh = Grid2D(nx = 3, ny = 1, dx = .5, dy = .1)
>>> var = CellVariable(value = (1, 2, 6), mesh = mesh)
>>> print var.getCellVolumeAverage()
3.0

getFaceGrad()¶: Return 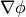$\nabla \phi$ as a rank-1 FaceVariable using differencing for the normal direction(second-order gradient).

getFaceGradAverage()¶: Return 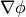$\nabla \phi$ as a rank-1 FaceVariable using averaging for the normal direction(second-order gradient)

getFaceValue()¶

Returns a FaceVariable whose value corresponds to the arithmetic interpolation of the adjacent cells:

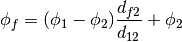
$\phi_f = (\phi_1 - \phi_2) \frac{d_{f2}}{d_{12}} + \phi_2$

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy import numerix
>>> mesh = Grid1D(dx = (1., 1.))
>>> L = 1
>>> R = 2
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getArithmeticFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = (R - L) * (0.5 / 1.) + L
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

>>> mesh = Grid1D(dx = (2., 4.))
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getArithmeticFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = (R - L) * (1.0 / 3.0) + L
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

>>> mesh = Grid1D(dx = (10., 100.))
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getArithmeticFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = (R - L) * (5.0 / 55.0) + L
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

getGaussGrad()¶: Return 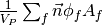$\frac{1}{V_P} \sum_f \vec{n} \phi_f A_f$ as a rank-1 CellVariable (first-order gradient).

getGlobalValue()¶

Concatenate and return values from all processors

When running on a single processor, the result is identical to getValue().

getGrad()¶: Return 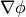$\nabla \phi$ as a rank-1 CellVariable (first-order gradient).

getHarmonicFaceValue()¶

Returns a FaceVariable whose value corresponds to the harmonic interpolation of the adjacent cells:

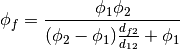
$\phi_f = \frac{\phi_1 \phi_2}{(\phi_2 - \phi_1) \frac{d_{f2}}{d_{12}} + \phi_1}$

>>> from fipy.meshes.grid1D import Grid1D
>>> from fipy import numerix
>>> mesh = Grid1D(dx = (1., 1.))
>>> L = 1
>>> R = 2
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getHarmonicFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = L * R / ((R - L) * (0.5 / 1.) + L)
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

>>> mesh = Grid1D(dx = (2., 4.))
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getHarmonicFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = L * R / ((R - L) * (1.0 / 3.0) + L)
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

>>> mesh = Grid1D(dx = (10., 100.))
>>> var = CellVariable(mesh = mesh, value = (L, R))
>>> faceValue = var.getHarmonicFaceValue()[mesh.getInteriorFaces().getValue()]
>>> answer = L * R / ((R - L) * (5.0 / 55.0) + L)
>>> print numerix.allclose(faceValue, answer, atol = 1e-10, rtol = 1e-10)
True

getLeastSquaresGrad()¶

Return 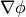$\nabla \phi$ , which is determined by solving for 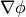$\nabla \phi$ in the following matrix equation,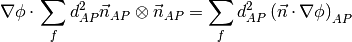

$\nabla \phi \cdot \sum_f d_{AP}^2 \vec{n}_{AP} \otimes \vec{n}_{AP} = \sum_f d_{AP}^2 \left( \vec{n} \cdot \nabla \phi \right)_{AP}$

The matrix equation is derived by minimizing the following least squares sum,

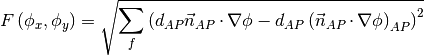
$F \left( \phi_x, \phi_y \right) = \sqrt{\sum_f \left( d_{AP} \vec{n}_{AP} \cdot \nabla \phi - d_{AP} \left( \vec{n}_{AP} \cdot \nabla \phi \right)_{AP} \right)^2 }$

Tests

>>> from fipy import Grid2D
>>> m = Grid2D(nx=2, ny=2, dx=0.1, dy=2.0)
>>> print numerix.allclose(CellVariable(mesh=m, value=(0,1,3,6)).getLeastSquaresGrad().getGlobalValue(), \
...                                     [[8.0, 8.0, 24.0, 24.0],
...                                      [1.2, 2.0, 1.2, 2.0]])
True

>>> from fipy import Grid1D
>>> print numerix.allclose(CellVariable(mesh=Grid1D(dx=(2.0, 1.0, 0.5)), 
...                                     value=(0, 1, 2)).getLeastSquaresGrad().getGlobalValue(), [[0.461538461538, 0.8, 1.2]])
True

getMinmodFaceValue()¶

Returns a FaceVariable with a value that is the minimum of the absolute values of the adjacent cells. If the values are of opposite sign then the result is zero:

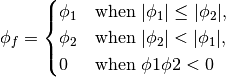
$\phi_f = \begin{cases} \phi_1& \text{when $|\phi_1| \le |\phi_2|$},\\ \phi_2& \text{when $|\phi_2| < |\phi_1|$},\\ 0 & \text{when $\phi1 \phi2 < 0$} \end{cases}$

>>> from fipy import *
>>> print CellVariable(mesh=Grid1D(nx=2), value=(1, 2)).getMinmodFaceValue()
[1 1 2]
>>> print CellVariable(mesh=Grid1D(nx=2), value=(-1, -2)).getMinmodFaceValue()
[-1 -1 -2]
>>> print CellVariable(mesh=Grid1D(nx=2), value=(-1, 2)).getMinmodFaceValue()
[-1  0  2]

getOld()¶

Return the values of the CellVariable from the previous solution sweep.

Combinations of CellVariable’s should also return old values.

>>> from fipy.meshes.grid1D import Grid1D
>>> mesh = Grid1D(nx = 2)
>>> from fipy.variables.cellVariable import CellVariable
>>> var1 = CellVariable(mesh = mesh, value = (2, 3), hasOld = 1)
>>> var2 = CellVariable(mesh = mesh, value = (3, 4))
>>> v = var1 * var2
>>> print v
[ 6 12]
>>> var1.setValue((3,2))
>>> print v
[9 8]
>>> print v.getOld()
[ 6 12]

The following small test is to correct for a bug when the operator does not just use variables.

>>> v1 = var1 * 3
>>> print v1
[9 6]
>>> print v1.getOld()
[6 9]

setValue(value, unit=None, where=None)¶

updateOld()¶: Set the values of the previous solution sweep to the current values.

The `cellVolumeAverageVariable` Module¶

The `constant` Module¶

The `exponentialNoiseVariable` Module¶

class fipy.variables.exponentialNoiseVariable.ExponentialNoiseVariable(mesh, mean=0.0, name='', hasOld=0)¶

Bases: fipy.variables.noiseVariable.NoiseVariable

Represents an exponential distribution of random numbers with the probability distribution

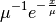
$\mu^{-1} e^{-\frac{x}{\mu}}$

with a mean parameter $\mu$ .

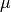We generate noise on a uniform cartesian mesh

>>> from fipy.variables.variable import Variable
>>> mean = Variable()
>>> from fipy.meshes.grid2D import Grid2D
>>> noise = ExponentialNoiseVariable(mesh = Grid2D(nx = 100, ny = 100), mean = mean)

We histogram the root-volume-weighted noise distribution

>>> from fipy.variables.histogramVariable import HistogramVariable
>>> histogram = HistogramVariable(distribution = noise, dx = 0.1, nx = 100)

and compare to a Gaussian distribution

>>> from fipy.variables.cellVariable import CellVariable
>>> expdist = CellVariable(mesh = histogram.getMesh())
>>> x = histogram.getMesh().getCellCenters()[0]

>>> if __name__ == '__main__':
...     from fipy import Viewer
...     viewer = Viewer(vars=noise, datamin=0, datamax=5)
...     histoplot = Viewer(vars=(histogram, expdist), 
...                        datamin=0, datamax=1.5)

>>> from fipy.tools.numerix import arange, exp

>>> for mu in arange(0.5,3,0.5):
...     mean.setValue(mu)
...     expdist.setValue((1/mean)*exp(-x/mean))
...     if __name__ == '__main__':
...         import sys
...         print >>sys.stderr, "mean: %g" % mean
...         viewer.plot()
...         histoplot.plot()

>>> print abs(noise.getFaceGrad().getDivergence().getCellVolumeAverage()) < 5e-15
1

random values with an exponential distribution

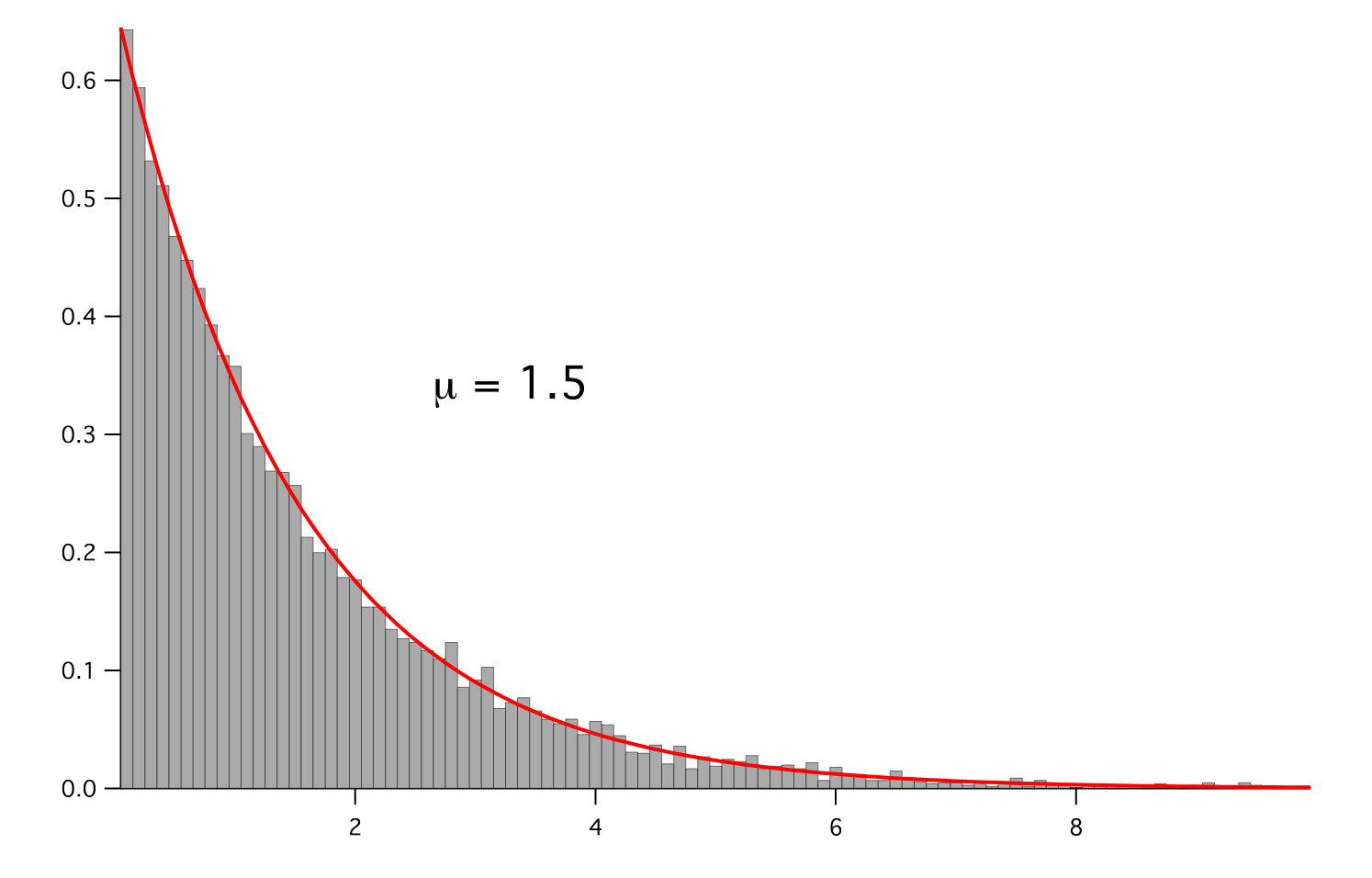
histogram of random values with an exponential distribution

Parameters :	mesh: The mesh on which to define the noise. mean: The mean of the distribution $\mu$ .

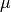random()¶

The `faceGradContributionsVariable` Module¶

The `faceGradVariable` Module¶

The `faceVariable` Module¶

class fipy.variables.faceVariable.FaceVariable(mesh, name='', value=0.0, rank=None, elementshape=None, unit=None, cached=1)¶

Bases: fipy.variables.meshVariable._MeshVariable

Parameters :	mesh: the mesh that defines the geometry of this Variable name: the user-readable name of the Variable value: the initial value rank: the rank (number of dimensions) of each element of this Variable. Default: 0 elementshape: the shape of each element of this variable Default: rank * (mesh.getDim(),) unit: the physical units of the Variable

copy()¶

getDivergence()¶

>>> from fipy.meshes.grid2D import Grid2D
>>> from fipy.variables.cellVariable import CellVariable
>>> mesh = Grid2D(nx=3, ny=2)
>>> var = CellVariable(mesh=mesh, value=range(3*2))
>>> print var.getFaceGrad().getDivergence()
[ 4.  3.  2. -2. -3. -4.]

getGlobalValue()¶

setValue(value, unit=None, where=None)¶

The `fixedBCFaceGradVariable` Module¶

The `gammaNoiseVariable` Module¶

class fipy.variables.gammaNoiseVariable.GammaNoiseVariable(mesh, shape, rate, name='', hasOld=0)¶

Bases: fipy.variables.noiseVariable.NoiseVariable

Represents a gamma distribution of random numbers with the probability distribution

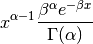
$x^{\alpha - 1}\frac{\beta^\alpha e^{-\beta x}}{\Gamma(\alpha)}$

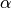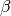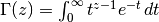with a shape parameter $\alpha$ , a rate parameter $\beta$ , and $\Gamma(z) = \int_0^\infty t^{z - 1}e^{-t}\,dt$ .

We generate noise on a uniform cartesian mesh

>>> from fipy.variables.variable import Variable
>>> alpha = Variable()
>>> beta = Variable()
>>> from fipy.meshes.grid2D import Grid2D
>>> noise = GammaNoiseVariable(mesh = Grid2D(nx = 100, ny = 100), shape = alpha, rate = beta)

We histogram the root-volume-weighted noise distribution

>>> from fipy.variables.histogramVariable import HistogramVariable
>>> histogram = HistogramVariable(distribution = noise, dx = 0.1, nx = 300)

and compare to a Gaussian distribution

>>> from fipy.variables.cellVariable import CellVariable
>>> gammadist = CellVariable(mesh = histogram.getMesh())
>>> x = histogram.getMesh().getCellCenters()[0]

>>> if __name__ == '__main__':
...     from fipy import Viewer
...     viewer = Viewer(vars=noise, datamin=0, datamax=30)
...     histoplot = Viewer(vars=(histogram, gammadist), 
...                        datamin=0, datamax=1)

>>> from fipy.tools.numerix import arange, exp
>>> from scipy.special import gamma as Gamma

>>> for shape in arange(1,8,1):
...     alpha.setValue(shape)
...     for rate in arange(0.5,2.5,0.5):
...         beta.setValue(rate)
...         gammadist.setValue(x**(alpha - 1) * (beta**alpha * exp(-beta * x)) / Gamma(alpha))
...         if __name__ == '__main__':
...             import sys
...             print >>sys.stderr, "alpha: %g, beta: %g" % (alpha, beta)
...             viewer.plot()
...             histoplot.plot()

>>> print abs(noise.getFaceGrad().getDivergence().getCellVolumeAverage()) < 5e-15
1

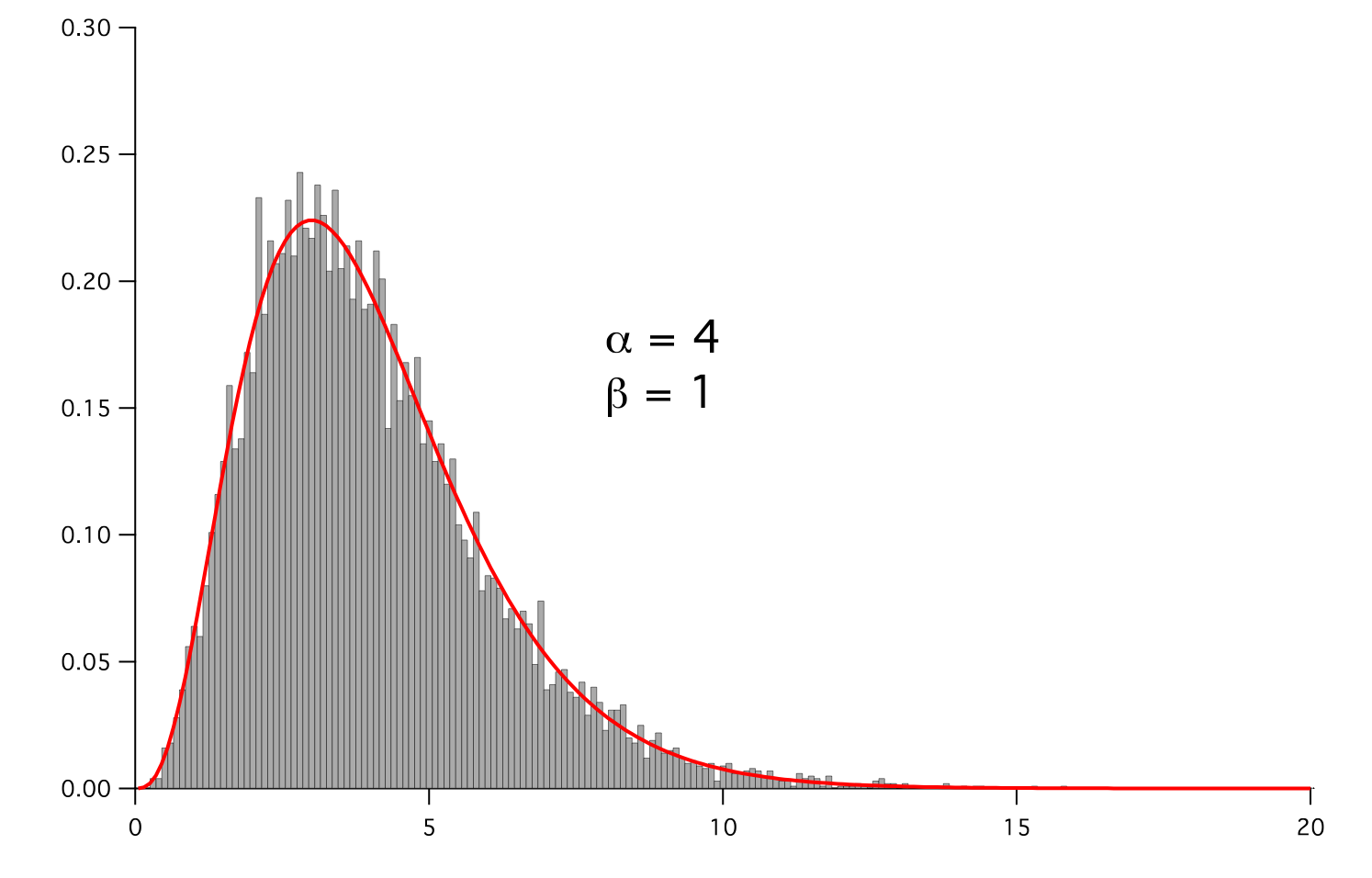
histogram of random values with a gamma distribution

Parameters :	mesh: The mesh on which to define the noise. shape: The shape parameter, 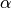$\alpha$ . rate: The rate or inverse scale parameter, $\beta$ .

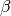random()¶

The `gaussCellGradVariable` Module¶

The `gaussianNoiseVariable` Module¶

class fipy.variables.gaussianNoiseVariable.GaussianNoiseVariable(mesh, name='', mean=0.0, variance=1.0, hasOld=0)¶

Bases: fipy.variables.noiseVariable.NoiseVariable

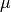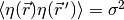Represents a normal (Gaussian) distribution of random numbers with mean $\mu$ and variance $\langle \eta(\vec{r}) \eta(\vec{r}\,') \rangle = \sigma^2$ , which has the probability distribution

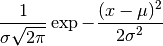
$\frac{1}{\sigma\sqrt{2\pi}} \exp -\frac{(x - \mu)^2}{2\sigma^2}$

For example, the variance of thermal noise that is uncorrelated in space and time is often expressed as

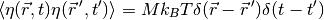
$\left\langle \eta(\vec{r}, t) \eta(\vec{r}\,', t') \right\rangle = M k_B T \delta(\vec{r} - \vec{r}\,')\delta(t - t')$

which can be obtained with:

sigmaSqrd = Mobility * kBoltzmann * Temperature / (mesh.getCellVolumes() * timeStep)
GaussianNoiseVariable(mesh = mesh, variance = sigmaSqrd)

Note

If the time step will change as the simulation progresses, either through use of an adaptive iterator or by making manual changes at different stages, remember to declare timeStep as a Variable and to change its value with its setValue() method.

>>> import sys
>>> from fipy.tools.numerix import *

>>> mean = 0.
>>> variance = 4.

We generate noise on a non-uniform cartesian mesh with cell dimensions of 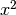$x^2$ and $y^3$ .

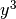>>> from fipy.meshes.grid2D import Grid2D
>>> mesh = Grid2D(dx = arange(0.1, 5., 0.1)**2, dy = arange(0.1, 3., 0.1)**3)
>>> from fipy.variables.cellVariable import CellVariable
>>> volumes = CellVariable(mesh=mesh,value=mesh.getCellVolumes())
>>> noise = GaussianNoiseVariable(mesh = mesh, mean = mean, 
...                               variance = variance / volumes)

We histogram the root-volume-weighted noise distribution

>>> from fipy.variables.histogramVariable import HistogramVariable
>>> histogram = HistogramVariable(distribution = noise * sqrt(volumes), 
...                               dx = 0.1, nx = 600, offset = -30)

and compare to a Gaussian distribution

>>> gauss = CellVariable(mesh = histogram.getMesh())
>>> x = histogram.getMesh().getCellCenters()[0]
>>> gauss.setValue((1/(sqrt(variance * 2 * pi))) * exp(-(x - mean)**2 / (2 * variance)))

>>> if __name__ == '__main__':
...     from fipy import viewers
...     viewer = Viewer(vars=noise, 
...                     datamin=-5, datamax=5)
...     histoplot = Viewer(vars=(histogram, gauss))

>>> for i in range(10):
...     noise.scramble()
...     if __name__ == '__main__':
...         viewer.plot()
...         histoplot.plot()

>>> print abs(noise.getFaceGrad().getDivergence().getCellVolumeAverage()) < 5e-15
1

Note that the noise exhibits larger amplitude in the small cells than in the large ones

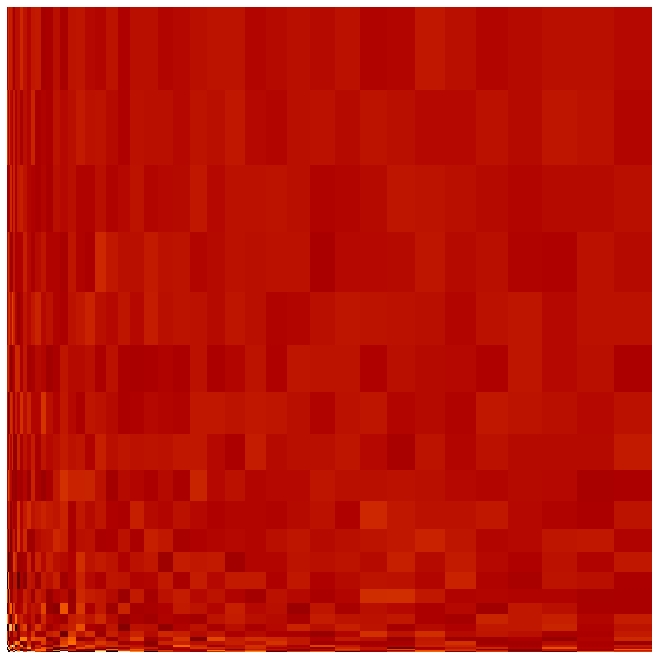
random values with a gaussian distribution

but that the root-volume-weighted histogram is Gaussian.

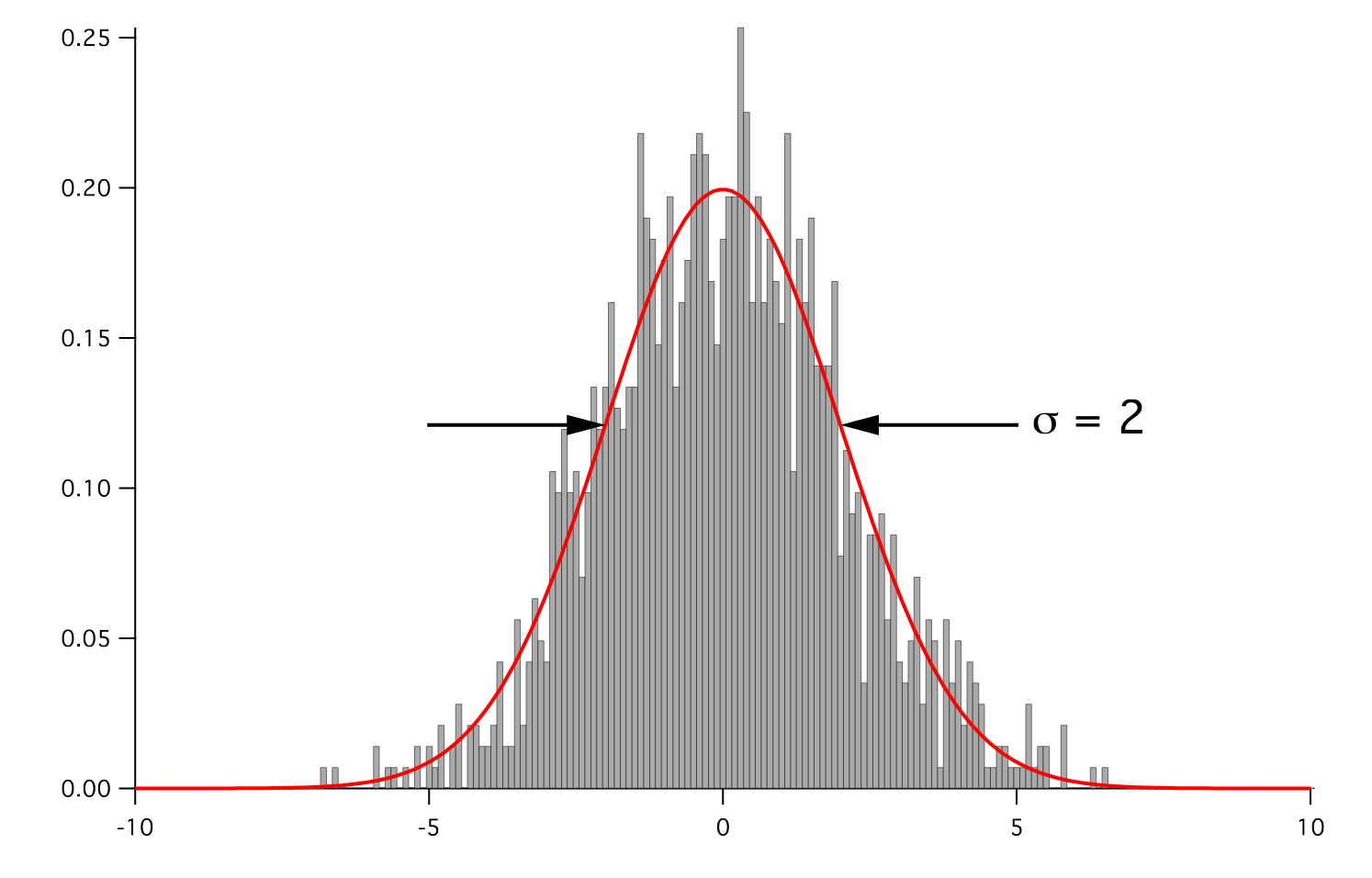
histogram of random values with a gaussian distribution

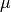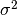Parameters :	mesh: The mesh on which to define the noise. mean: The mean of the noise distrubution, $\mu$ . variance: The variance of the noise distribution, $\sigma^2$ .

parallelRandom()¶

The `harmonicCellToFaceVariable` Module¶

The `histogramVariable` Module¶

class fipy.variables.histogramVariable.HistogramVariable(distribution, dx=1.0, nx=None, offset=0.0)¶

Bases: fipy.variables.cellVariable.CellVariable

Produces a histogram of the values of the supplied distribution.

Parameters :	distribution: The collection of values to sample. dx: the bin size nx: the number of bins offset: the position of the first bin

The `leastSquaresCellGradVariable` Module¶

The `meshVariable` Module¶

The `minmodCellToFaceVariable` Module¶

The `modCellGradVariable` Module¶

The `modCellToFaceVariable` Module¶

The `modFaceGradVariable` Module¶

The `modPhysicalField` Module¶

The `modularVariable` Module¶

class fipy.variables.modularVariable.ModularVariable(mesh, name='', value=0.0, rank=None, elementshape=None, unit=None, hasOld=0)¶

Bases: fipy.variables.cellVariable.CellVariable

The ModularVariable defines a variable that exisits on the circle between 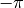$-\pi$ and $\pi$

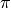
The following examples show how ModularVariable works. When subtracting the answer wraps back around the circle.

>>> from fipy.meshes.grid1D import Grid1D
>>> mesh = Grid1D(nx = 2)
>>> from fipy.tools import numerix
>>> pi = numerix.pi
>>> v1 = ModularVariable(mesh = mesh, value = (2*pi/3, -2*pi/3))
>>> v2 = ModularVariable(mesh = mesh, value = -2*pi/3)
>>> print numerix.allclose(v2 - v1, (2*pi/3, 0))
1

Obtaining the arithmetic face value.

>>> print numerix.allclose(v1.getArithmeticFaceValue(), (2*pi/3, pi, -2*pi/3))
1

Obtaining the gradient.

>>> print numerix.allclose(v1.getGrad(), ((pi/3, pi/3),))
1

Obtaining the gradient at the faces.

>>> print numerix.allclose(v1.getFaceGrad(), ((0, 2*pi/3, 0),))
1

Obtaining the gradient at the faces but without modular arithmetic.

>>> print numerix.allclose(v1.getFaceGradNoMod(), ((0, -4*pi/3, 0),))
1

getArithmeticFaceValue()¶

Returns a FaceVariable whose value corresponds to the arithmetic interpolation of the adjacent cells:

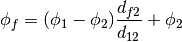
$\phi_f = (\phi_1 - \phi_2) \frac{d_{f2}}{d_{12}} + \phi_2$

Adjusted for a ModularVariable

getFaceGrad()¶: Return 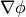$\nabla \phi$ as a rank-1 FaceVariable (second-order gradient). Adjusted for a ModularVariable

getFaceGradNoMod()¶: Return 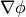$\nabla \phi$ as a rank-1 FaceVariable (second-order gradient). Not adjusted for a ModularVariable

getGrad()¶: Return 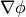$\nabla \phi$ as a rank-1 CellVariable (first-order gradient). Adjusted for a ModularVariable

updateOld()¶

Set the values of the previous solution sweep to the current values. Test case due to bug.

>>> from fipy.meshes.grid1D import Grid1D
>>> mesh = Grid1D(nx = 1)
>>> var = ModularVariable(mesh=mesh, value=1., hasOld=1)
>>> var.updateOld()
>>> var[:] = 2
>>> answer = CellVariable(mesh=mesh, value=1.)
>>> print var.getOld().allclose(answer)
True

The `noiseVariable` Module¶

class fipy.variables.noiseVariable.NoiseVariable(mesh, name='', hasOld=0)¶

Bases: fipy.variables.cellVariable.CellVariable

Attention

This class is abstract. Always create one of its subclasses.

A generic base class for sources of noise distributed over the cells of a mesh.

In the event that the noise should be conserved, use:

<Specific>NoiseVariable(...).getFaceGrad().getDivergence()

The seed() and get_seed() functions of the fipy.tools.numerix.random module can be set and query the random number generated used by all NoiseVariable objects.

copy()¶: Copy the value of the NoiseVariable to a static CellVariable.

parallelRandom()¶

random()¶

scramble()¶: Generate a new random distribution.

The `operatorVariable` Module¶

The `scharfetterGummelFaceVariable` Module¶

class fipy.variables.scharfetterGummelFaceVariable.ScharfetterGummelFaceVariable(var, boundaryConditions=())¶: Bases: fipy.variables.cellToFaceVariable._CellToFaceVariable

The `test` Module¶

Test numeric implementation of the mesh

The `unaryOperatorVariable` Module¶

The `uniformNoiseVariable` Module¶

class fipy.variables.uniformNoiseVariable.UniformNoiseVariable(mesh, name='', minimum=0.0, maximum=1.0, hasOld=0)¶

Bases: fipy.variables.noiseVariable.NoiseVariable

Represents a uniform distribution of random numbers.

We generate noise on a uniform cartesian mesh

>>> from fipy.meshes.grid2D import Grid2D
>>> noise = UniformNoiseVariable(mesh=Grid2D(nx=100, ny=100))

and histogram the noise

>>> from fipy.variables.histogramVariable import HistogramVariable
>>> histogram = HistogramVariable(distribution=noise, dx=0.01, nx=120, offset=-.1)

>>> if __name__ == '__main__':
...     from fipy import Viewer
...     viewer = Viewer(vars=noise, 
...                     datamin=0, datamax=1)
...     histoplot = Viewer(vars=histogram)

>>> for i in range(10):
...     noise.scramble()
...     if __name__ == '__main__':
...         viewer.plot()
...         histoplot.plot()

random values with a uniform distribution

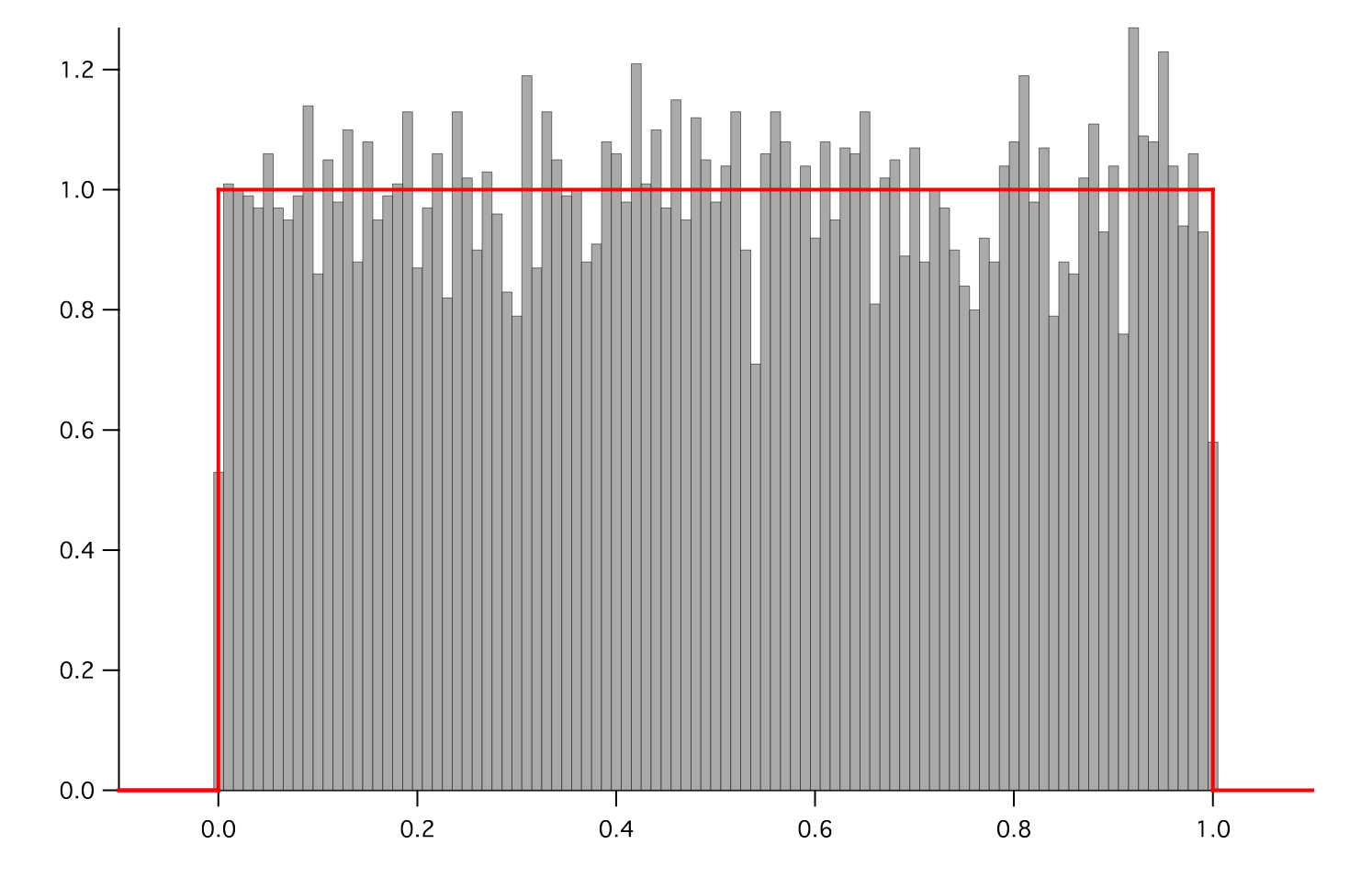
histogram of random values with a uniform distribution

Parameters :	mesh: The mesh on which to define the noise. minimum: The minimum (not-inclusive) value of the distribution. maximum: The maximum (not-inclusive) value of the distribution.

random()¶

The `variable` Module¶

class fipy.variables.variable.Variable(value=0.0, unit=None, array=None, name='', cached=1)¶

Bases: object

Lazily evaluated quantity with units.

Using a Variable in a mathematical expression will create an automatic dependency Variable, e.g.,

>>> a = Variable(value=3)
>>> b = 4 * a
>>> b
(Variable(value=array(3)) * 4)
>>> b()
12

Changes to the value of a Variable will automatically trigger changes in any dependent Variable objects

>>> a.setValue(5)
>>> b
(Variable(value=array(5)) * 4)
>>> b()
20

Create a Variable.

>>> Variable(value=3)
Variable(value=array(3))
>>> Variable(value=3, unit="m")
Variable(value=PhysicalField(3,'m'))
>>> Variable(value=3, unit="m", array=numerix.zeros((3,2)))
Variable(value=PhysicalField(array([[3, 3],
       [3, 3],
       [3, 3]]),'m'))

Parameters :	value: the initial value unit: the physical units of the Variable array: the storage array for the Variable name: the user-readable name of the Variable cached: whether to cache or always recalculate the value

all(axis=None)¶

>>> print Variable(value=(0, 0, 1, 1)).all()
0
>>> print Variable(value=(1, 1, 1, 1)).all()
1

allclose(other, rtol=1e-05, atol=1e-08)¶

>>> var = Variable((1, 1))
   >>> print var.allclose((1, 1))
   1
   >>> print var.allclose((1,))
   1

The following test is to check that the system does not run out of memory.

>>> from fipy.tools import numerix
>>> var = Variable(numerix.ones(10000))
>>> print var.allclose(numerix.zeros(10000))
False

allequal(other)¶

any(axis=None)¶

>>> print Variable(value=0).any()
0
>>> print Variable(value=(0, 0, 1, 1)).any()
1

arccos()¶

arccosh()¶

arcsin()¶

arcsinh()¶

arctan()¶

arctan2(other)¶

arctanh()¶

cacheMe(recursive=False)¶

ceil()¶

conjugate()¶

copy()¶

Make an duplicate of the Variable

>>> a = Variable(value=3)
>>> b = a.copy()
>>> b
Variable(value=array(3))

The duplicate will not reflect changes made to the original

>>> a.setValue(5)
>>> b
Variable(value=array(3))

Check that this works for arrays.

>>> a = Variable(value=numerix.array((0,1,2)))
>>> b = a.copy()
>>> b
Variable(value=array([0, 1, 2]))
>>> a[1] = 3
>>> b
Variable(value=array([0, 1, 2]))

cos()¶

cosh()¶

dontCacheMe(recursive=False)¶

dot(other, opShape=None, operatorClass=None, axis=0)¶

exp()¶

floor()¶

getMag()¶

getName()¶

getNumericValue()¶

getShape()¶

>>> Variable(value=3).shape
()
>>> Variable(value=(3,)).shape
(1,)
>>> Variable(value=(3,4)).shape
(2,)

>>> Variable(value="3 m").shape
()
>>> Variable(value=(3,), unit="m").shape
(1,)
>>> Variable(value=(3,4), unit="m").shape
(2,)

getSubscribedVariables()¶

getUnit()¶

Return the unit object of self.

>>> Variable(value="1 m").getUnit()
<PhysicalUnit m>

getValue()¶

“Evaluate” the Variable and return its value (longhand)

>>> a = Variable(value=3)
>>> print a.getValue()
3
>>> b = a + 4
>>> b
(Variable(value=array(3)) + 4)
>>> b.getValue()
7

getsctype(default=None)¶

Returns the Numpy sctype of the underlying array.

>>> Variable(1).getsctype() == numerix.NUMERIX.obj2sctype(numerix.array(1))
True
>>> Variable(1.).getsctype() == numerix.NUMERIX.obj2sctype(numerix.array(1.))
True
>>> Variable((1,1.)).getsctype() == numerix.NUMERIX.obj2sctype(numerix.array((1., 1.)))
True

inBaseUnits()¶

Return the value of the Variable with all units reduced to their base SI elements.

>>> e = Variable(value="2.7 Hartree*Nav")
>>> print e.inBaseUnits()
7088849.01085 kg*m**2/s**2/mol

inUnitsOf(*units)¶

Returns one or more Variable objects that express the same physical quantity in different units. The units are specified by strings containing their names. The units must be compatible with the unit of the object. If one unit is specified, the return value is a single Variable.

>>> freeze = Variable('0 degC')
>>> print freeze.inUnitsOf('degF')
32.0 degF

If several units are specified, the return value is a tuple of Variable instances with with one element per unit such that the sum of all quantities in the tuple equals the the original quantity and all the values except for the last one are integers. This is used to convert to irregular unit systems like hour/minute/second. The original object will not be changed.

>>> t = Variable(value=314159., unit='s')
>>> [str(element) for element in t.inUnitsOf('d','h','min','s')]
['3.0 d', '15.0 h', '15.0 min', '59.0 s']

itemset(value)¶

log()¶

log10()¶

max(axis=None)¶

min(axis=None)¶

put(indices, value)¶

reshape(shape)¶

setName(name)¶

setUnit(unit)¶

Change the unit object of self to unit

>>> a = Variable(value="1 m")
>>> a.setUnit("m**2/s")
>>> print a
1.0 m**2/s

setValue(value, unit=None, where=None)¶

Set the value of the Variable. Can take a masked array.

>>> a = Variable((1,2,3))
>>> a.setValue(5, where=(1, 0, 1))
>>> print a
[5 2 5]

>>> b = Variable((4,5,6))
>>> a.setValue(b, where=(1, 0, 1))
>>> print a
[4 2 6]
>>> print b
[4 5 6]
>>> a.setValue(3)
>>> print a
[3 3 3]

>>> b = numerix.array((3,4,5))
>>> a.setValue(b)
>>> a[:] = 1
>>> print b
[3 4 5]

>>> a.setValue((4,5,6), where=(1, 0)) 
Traceback (most recent call last):
    ....
ValueError: shape mismatch: objects cannot be broadcast to a single shape

shape¶: Tuple of array dimensions.

sign()¶

sin()¶

sinh()¶

sqrt()¶

>>> from fipy.meshes.grid1D import Grid1D
>>> mesh= Grid1D(nx=3)

>>> from fipy.variables.cellVariable import CellVariable
>>> var = CellVariable(mesh=mesh, value=((0., 2., 3.),), rank=1)
>>> print (var.dot(var)).sqrt()
[ 0.  2.  3.]

sum(axis=None)¶

take(ids, axis=0)¶

tan()¶

tanh()¶

tostring(max_line_width=75, precision=8, suppress_small=False, separator=' ')¶

transpose()¶: It is not longer needed.

Table Of Contents

Previous topic

Next topic

This Page

Contact

`variables` Package Documentation¶

The `addOverFacesVariable` Module¶

The `arithmeticCellToFaceVariable` Module¶

The `betaNoiseVariable` Module¶

The `binaryOperatorVariable` Module¶

The `cellToFaceVariable` Module¶

The `cellVariable` Module¶

The `cellVolumeAverageVariable` Module¶

The `constant` Module¶

The `exponentialNoiseVariable` Module¶

The `faceGradContributionsVariable` Module¶

The `faceGradVariable` Module¶

The `faceVariable` Module¶

The `fixedBCFaceGradVariable` Module¶

The `gammaNoiseVariable` Module¶

The `gaussCellGradVariable` Module¶

The `gaussianNoiseVariable` Module¶

The `harmonicCellToFaceVariable` Module¶

The `histogramVariable` Module¶

The `leastSquaresCellGradVariable` Module¶

The `meshVariable` Module¶

The `minmodCellToFaceVariable` Module¶

The `modCellGradVariable` Module¶

The `modCellToFaceVariable` Module¶

The `modFaceGradVariable` Module¶

The `modPhysicalField` Module¶

The `modularVariable` Module¶

The `noiseVariable` Module¶

The `operatorVariable` Module¶

The `scharfetterGummelFaceVariable` Module¶

The `test` Module¶

The `unaryOperatorVariable` Module¶

The `uniformNoiseVariable` Module¶

The `variable` Module¶

Navigation

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Contact

variables Package Documentation¶

The addOverFacesVariable Module¶

The arithmeticCellToFaceVariable Module¶

The betaNoiseVariable Module¶

The binaryOperatorVariable Module¶

The cellToFaceVariable Module¶

The cellVariable Module¶

The cellVolumeAverageVariable Module¶

The constant Module¶

The exponentialNoiseVariable Module¶

The faceGradContributionsVariable Module¶

The faceGradVariable Module¶

The faceVariable Module¶

The fixedBCFaceGradVariable Module¶

The gammaNoiseVariable Module¶

The gaussCellGradVariable Module¶

The gaussianNoiseVariable Module¶

The harmonicCellToFaceVariable Module¶

The histogramVariable Module¶

The leastSquaresCellGradVariable Module¶

The meshVariable Module¶

The minmodCellToFaceVariable Module¶

The modCellGradVariable Module¶

The modCellToFaceVariable Module¶

The modFaceGradVariable Module¶

The modPhysicalField Module¶

The modularVariable Module¶

The noiseVariable Module¶

The operatorVariable Module¶

The scharfetterGummelFaceVariable Module¶

The test Module¶

The unaryOperatorVariable Module¶

The uniformNoiseVariable Module¶

The variable Module¶

`variables` Package Documentation¶

The `addOverFacesVariable` Module¶

The `arithmeticCellToFaceVariable` Module¶

The `betaNoiseVariable` Module¶

The `binaryOperatorVariable` Module¶

The `cellToFaceVariable` Module¶

The `cellVariable` Module¶

The `cellVolumeAverageVariable` Module¶

The `constant` Module¶

The `exponentialNoiseVariable` Module¶

The `faceGradContributionsVariable` Module¶

The `faceGradVariable` Module¶

The `faceVariable` Module¶

The `fixedBCFaceGradVariable` Module¶

The `gammaNoiseVariable` Module¶

The `gaussCellGradVariable` Module¶

The `gaussianNoiseVariable` Module¶

The `harmonicCellToFaceVariable` Module¶

The `histogramVariable` Module¶

The `leastSquaresCellGradVariable` Module¶

The `meshVariable` Module¶

The `minmodCellToFaceVariable` Module¶

The `modCellGradVariable` Module¶

The `modCellToFaceVariable` Module¶

The `modFaceGradVariable` Module¶

The `modPhysicalField` Module¶

The `modularVariable` Module¶

The `noiseVariable` Module¶

The `operatorVariable` Module¶

The `scharfetterGummelFaceVariable` Module¶

The `test` Module¶

The `unaryOperatorVariable` Module¶

The `uniformNoiseVariable` Module¶

The `variable` Module¶