µMAG Standard Problem #3
Problem proposed by Alex Hubert, University of Erlangen-Nuremberg.
Please send comments
to [email protected] and
join the µMAG discussion e-mail list for
ongoing discussion.
A set of solutions have been submitted.
Specifications
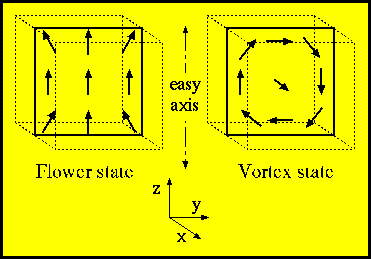
This problem is to calculate the single domain limit of a cubic magnetic
particle. This is the size L of equal energy for the so-called flower
state (which one may also call a splayed state or a modified
single-domain state) on the one hand, and the vortex or curling state on
the other hand.
Geometry:
A cube with edge length, L, expressed in units of the
intrinsic length scale, lex =
(A/Km)1/2, where
Km is a magnetostatic energy density,
Km =
1/2µ0Ms2
(SI) or 2piMs2 (cgs emu).
Material parameters:
Uniaxial anisotropy Ku with
Ku = 0.1 Km, and with the easy axis
directed parallel to a principal axis of the cube.
Desired output for comparison:
- The indicated "single domain limit," L where the
energy of the flower state is equal to the energy of the
vortex state.
- The partial energies (exchange, stray field, anisotropy) all
in units of Km.
- The average magnetization along the three axes.
All these values should be given for both configurations (flower and
vortex) at the single domain size.
The results should be shown to be independent of the discretization size.
Please see the µMAG standard problem strategy
page for information on publicizing your results.
Comments:
The transition is expected to be found in the neighborhood of
L = 8 lex.
Site Directory
µMAG organization / NIST CTCMS /
[email protected]
20-MAR-1998
