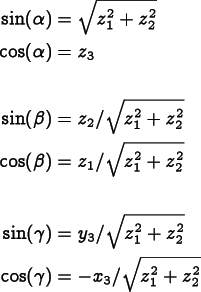OOF2: The Manual
Name
Abg (Abg) — Euler angles (alpha, beta, gamma) are applied: first beta about the z axis, then alpha about the y, and finally gamma about z. This operation brings the crystal axes into coincidence with the lab axes.
Synopsis
Abg(alpha,beta,gamma)
Details
-
Base class:
Orientation -
Parameters:
alpha- second rotation, about the y-axis, in degrees. Type: A real number in the range [0, 180].
beta- first rotation, about the z-axis, in degrees. Type: A real number in the range [-180, 180].
gamma- third rotation, about the z-axis, in degrees. Type: A real number in the range [-180, 180].
Description
An Abg object represents the orientation of
a three dimensional object (assumed to be a crystal in this
discussion) in three dimensional space in terms of the Euler
angles
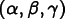 . The literature contains different ways of
interpreting the angles. Here we present four different, but
equivalent, prescriptions for determining the actual rotation
described by the three angles, as used in the
. The literature contains different ways of
interpreting the angles. Here we present four different, but
equivalent, prescriptions for determining the actual rotation
described by the three angles, as used in the
Abg class.
We define 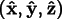 to be the screen coordinate system, with
to be the screen coordinate system, with
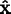 pointing to the
right,
pointing to the
right,
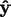 upwards, and
upwards, and
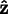 out of the screen. We will call
the crystal axes
out of the screen. We will call
the crystal axes
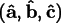 .
As usual, all rotations are right handed -- a positive rotation
about an axis is counterclockwise if the axis is pointed towards
you.
.
As usual, all rotations are right handed -- a positive rotation
about an axis is counterclockwise if the axis is pointed towards
you.
One Method of Finding the Euler Angles:
This method describes the rotation that must be applied to the
crystal axes to bring them into alignment with the screen axes,
assuming that the crystal starts in its
desired orientation with respect to the screen. First, rotate
the axes by
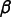 around the
around the
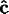 axis. This defines new axes
axis. This defines new axes
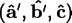 .
Next rotate by
.
Next rotate by
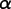 about the
about the
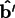 axis, defining another coordinate system
axis, defining another coordinate system
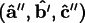 .
Finally, rotate by
.
Finally, rotate by
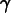 about the
about the
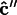 axis, bringing the axes into agreement with
axis, bringing the axes into agreement with
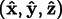 .
.
An equivalent method:
Consider the material oriented with a globe, with the origin at
the center of the earth and
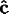 -axis pointing towards the
north pole, the
-axis pointing towards the
north pole, the
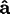 -axis pointing at the Greenwich Meridian
where it intersects the equator and the
-axis pointing at the Greenwich Meridian
where it intersects the equator and the
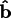 -axis pointing
towards the Indian ocean somewhere southeast of Sri Lanka. The
unrotated globe has its
-axis pointing
towards the Indian ocean somewhere southeast of Sri Lanka. The
unrotated globe has its
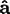 ,
,
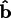 , and
, and
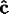 axes aligned
with the
axes aligned
with the
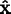 ,
,
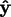 , and
, and
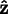 axes of the screen,
respectively. The rotation triplet describes how to rotate the
material into its desired orientation (in contrast to the
previous method, which started with the
material in its desired orientation). The first number of the
rotation triplet tilts the point on the north pole southward
along the Greenwich Meridian by -
axes of the screen,
respectively. The rotation triplet describes how to rotate the
material into its desired orientation (in contrast to the
previous method, which started with the
material in its desired orientation). The first number of the
rotation triplet tilts the point on the north pole southward
along the Greenwich Meridian by -
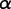 degrees to a new
latitude. The second number spins the globe to the east by
degrees to a new
latitude. The second number spins the globe to the east by
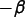 degrees about its (tilted)
degrees about its (tilted)
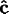 -axis. The third number
rotates the tilted globe to the east by
-axis. The third number
rotates the tilted globe to the east by 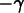 degrees about the screen's
degrees about the screen's
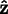 axis.
axis.
A third method:
The order of rotations in the previous definition can be
rearranged. Rotate the globe to the east by 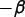 degrees about
the
degrees about
the
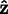 -axis, tilt the north pole by
-axis, tilt the north pole by 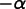 about the
about the
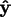 -axis, and rotate to the east by
-axis, and rotate to the east by 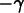 again about the
again about the
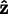 -axis.
-axis.
The fourth method:
If you know the components in the crystal coordinate system of
the screen vectors
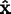 ,
,
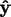 , and
, and
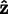 , you can compute
the Euler angles as follows. Let
, you can compute
the Euler angles as follows. Let
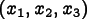 be the components of the screen's
be the components of the screen's
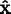 -axis in the crystal
coordinate system. Let
-axis in the crystal
coordinate system. Let
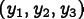 and
and
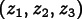 similarly be the components of the
similarly be the components of the
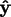 and
and
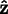 -axes. Then
-axes. Then